Abstract
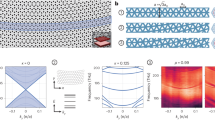
Synthetic magnetism has been used to control charge neutral excitations for applications ranging from classical beam steering to quantum simulation. In optomechanics, radiation-pressure-induced parametric coupling between optical (photon) and mechanical (phonon) excitations may be used to break time-reversal symmetry, providing the prerequisite for synthetic magnetism. Here we design and fabricate a silicon optomechanical circuit with both optical and mechanical connectivity between two optomechanical cavities. Driving the two cavities with phase-correlated laser light results in a synthetic magnetic flux, which, in combination with dissipative coupling to the mechanical bath, leads to non-reciprocal transport of photons with 35 dB of isolation. Additionally, optical pumping with blue-detuned light manifests as a particle non-conserving interaction between photons and phonons, resulting in directional optical amplification of 12 dB in the isolator through-direction. These results suggest the possibility of using optomechanical circuits to create a more general class of non-reciprocal optical devices, and further, to enable new topological phases for both light and sound on a microchip.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Dalibard, J., Gerbier, F., Juzelinas, G. & Öhberg, P. Colloquium: artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 83, 1523–1543 (2011).
Koch, J., Houck, A., Hur, K. L. & Girvin, S. Time-reversal-symmetry breaking in circuit-QED-based photon lattices. Phys. Rev. A 82, 043811 (2010).
Sliwa, K. et al. Reconfigurable Josephson circulator/directional amplifier. Phys. Rev. X 5, 041020 (2015).
Roushan, P. et al. Chiral groundstate currents of interacting photons in a synthetic magnetic field. Nat. Phys. http://dx.doi.org/10.1038/nphys3930 (2016).
Umucalılar, R. & Carusotto, I. Artificial gauge field for photons in coupled cavity arrays. Phys. Rev. A 84, 043804 (2011).
Hafezi, M., Demler, E., Lukin, M. & Taylor, J. Robust optical delay lines with topological protection. Nat. Phys. 7, 907–912 (2011).
Fang, K., Yu, Z. & Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photon. 6, 782–787 (2012).
Rechtsman, M. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).
Tzuang, L., Fang, K., Nussenzveig, P., Fan, S. & Lipson, M. Nonreciprocal phase shift induced by an effective magnetic flux for light. Nat. Photon. 8, 701–705 (2014).
Lin, Y.-J., Compton, R., Jimnez-Garca, K., Porto, J. & Spielman, I. Synthetic magnetic fields for ultracold neutral atoms. Nature 462, 628–632 (2009).
Ray, M. W., Ruokokoski, E., Kandel, S., Möttönen, M. & Hall, D. S. Observation of Dirac monopoles in a synthetic magnetic field. Nature 505, 657–660 (2014).
Lu, L., Joannopoulos, J. & Soljai, M. Topological photonics. Nat. Photon. 8, 821–829 (2014).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Rosenberg, J., Lin, Q. & Painter, O. Static and dynamic wavelength routing via the gradient optical force. Nat. Photon. 3, 478–483 (2009).
Manipatruni, S., Robinson, J. T. & Lipson, M. Optical nonreciprocity in optomechanical structures. Phys. Rev. Lett. 102, 213903 (2009).
Hafezi, M. & Rabl, P. Optomechanically induced non-reciprocity in microring resonators. Opt. Exp. 20, 7672–7684 (2012).
Habraken, S. J. M., Stannigel, K., Lukin, M. D., Zoller, P. & Rabl, P. Continuous mode cooling and phonon routers for phononic quantum networks. New J. Phys. 14, 115004 (2012).
Wang, Z., Shi, L., Liu, Y., Xu, X. & Zhang, X. Optical nonreciprocity in asymmetric optomechanical couplers. Sci. Rep. 5, 8657 (2015).
Peano, V., Brendel, C., Schmidt, M. & Marquardt, F. Topological phases of sound and light. Phys. Rev. X 5, 031011 (2015).
Schmidt, M., Keßler, S., Peano, V., Painter, O. & Marquardt, F. Optomechanical creation of magnetic fields for photons on a lattice. Optica 2, 635–641 (2015).
Fang, K., Matheny, M. H., Luan, X. & Painter, O. Optical transduction and routing of microwave phonons in cavity-optomechanical circuits. Nat. Photon. 10, 489–496 (2016).
Kim, J., Kuzyk, M. C., Han, K., Wang, H. & Bahl, G. Non-reciprocal Brillouin scattering induced transparency. Nat. Phys. 11, 275–280 (2015).
Shen, Z. et al. Experimental realization of optomechanically induced non-reciprocity. Nat. Photon. 10, 657–661 (2016).
Ruesink, F., Miri, M.-A., Alú, A. & Verhagen, E. Nonreciprocity and magnetic-free isolation based on optomechanical interactions. Nat. Commun. 7, 13662 (2016).
Metelmann, A. & Clerk, A. Nonreciprocal photon transmission and amplification via reservoir engineering. Phys. Rev. X 5, 021025 (2015).
Abdo, B., Sliwa, K., Frunzio, L. & Devoret, M. Directional amplification with a Josephson circuit. Phys. Rev. X 3, 031001 (2013).
Abdo, B. et al. Josephson directional amplifier for quantum measurement of superconducting circuits. Phys. Rev. Lett. 112, 167701 (2014).
Peano, V., Houde, M., Brendel, C., Marquardt, F. & Clerk, A. Topological phase transitions and chiral inelastic transport induced by the squeezing of light. Nat. Commun. 7, 10779 (2016).
Peano, V., Houde, M., Marquardt, F. & Clerk, A. A. Topological quantum fluctuations and travelling wave amplifiers. Phys. Rev. X 6, 041026 (2016).
Boada, O., Celi, A., Latorre, J. I. & Lewenstein, M. Quantum simulation of an extra dimension. Phys. Rev. Lett. 108, 133001 (2012).
Celi, A. et al. Synthetic gauge fields in synthetic dimensions. Phys. Rev. Lett. 112, 043001 (2014).
Mancini, M. et al. Observation of chiral edge states with neutral fermions in synthetic Hall ribbons. Science 349, 1510–1513 (2015).
Stuhl, B. K., Lu, H.-I., Aycock, L. M., Genkina, D. & Spielman, I. B. Visualizing edge states with an atomic Bose gas in the quantum Hall regime. Science 349, 1514–1518 (2015).
Fang, K., Yu, Z. & Fan, S. Photonic Aharonov–Bohm effect based on dynamic modulation. Phys. Rev. Lett. 108, 153901 (2012).
Aharanov, Y. & Bohm, D. Signigicance of electromagnetic potentials in the quantum theory. Phys. Rev. 115, 485–491 (1959).
Deák, L. & Fülöp, T. Reciprocity in quantum, electromagnetic and other wave scattering. Ann. Phys. 327, 1050–1077 (2012).
Eichenfield, M., Chan, J., Camacho, R. M., Vahala, K. J. & Painter, O. Optomechanical crystals. Nature 462, 78–82 (2009).
Sadat-Saleh, S., Benchabane, S., Baida, F. I., Bernal, M.-P. & Laude, V. Tailoring simultaneous photonic and phononic band gaps. J. Appl. Phys. 106, 074912 (2009).
Gomis-Bresco, J. et al. A one-dimensional optomechanical crystal with a complete phononic band gap. Nat. Commun. 5, 4452 (2014).
Safavi-Naeini, A. H. & Painter, O. Design of optomechanical cavities and waveguides on a simultaneous bandgap phononic-photonic crystal slab. Opt. Exp. 18, 14926–14943 (2010).
Sato, Y. et al. Strong coupling between distant photonic nanocavities and its dynamic control. Nat. Photon. 6, 56–61 (2012).
Gröblacher, S., Hill, J. T., Safavi-Naeini, A. H., Chan, J. & Painter, O. Highly efficient coupling from an optical fiber to a nanoscale silicon optomechanical cavity. Appl. Phys. Lett. 108, 181104 (2013).
Chan, J., Safavi-Naeini, A. H., Hill, J. T., Meenehan, S. & Painter, O. Optimized optomechanical crystal cavity with acoustic radiation shield. Appl. Phys. Lett. 101, 081115 (2012).
Meenehan, S. M. et al. Silicon optomechanical crystal resonator at millikelvin temperatures. Phys. Rev. A 90, 011803 (2014).
Walter, S. & Marquardt, F. Classical dynamical gauge fields in optomechanics. New J. Phys. 18, 113029 (2016).
Acknowledgements
The authors would like to thank M. Roukes for the use of his atomic force microscope in the nano-oxidation tuning of the cavities. This work was supported by the AFOSR-MURI Quantum Photonic Matter, the ARO-MURI Quantum Opto-Mechanics with Atoms and Nanostructured Diamond (grant N00014-15-1-2761), the University of Chicago Quantum Engineering Program (A.A.C., A.M.), the ERC Starting Grant OPTOMECH (F.M.), the Institute for Quantum Information and Matter, an NSF Physics Frontiers Center (grant PHY-1125565) with support of the Gordon and Betty Moore Foundation, and the Kavli Nanoscience Institute at Caltech.
Author information
Authors and Affiliations
Contributions
K.F., F.M., A.M., A.A.C. and O.P. came up with the concept. K.F., O.P. and J.L. planned the experiment. K.F., J.L. and M.H.M. performed the device design and fabrication. K.F. and J.L. performed the measurements. K.F., J.L., A.M., A.A.C. and O.P. analysed the data. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1178 kb)
Rights and permissions
About this article
Cite this article
Fang, K., Luo, J., Metelmann, A. et al. Generalized non-reciprocity in an optomechanical circuit via synthetic magnetism and reservoir engineering. Nature Phys 13, 465–471 (2017). https://doi.org/10.1038/nphys4009
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys4009
This article is cited by
-
Integrated passive nonlinear optical isolators
Nature Photonics (2023)
-
Quadrature nonreciprocity in bosonic networks without breaking time-reversal symmetry
Nature Physics (2023)
-
Noiseless single-photon isolator at room temperature
Communications Physics (2023)
-
Enhanced nonlinear optomechanics in a coupled-mode photonic crystal device
Nature Communications (2023)
-
A giant atom with modulated transition frequency
Frontiers of Physics (2023)