Abstract
Many marine invertebrates have larval stages covered in linear arrays of beating cilia, which propel the animal while simultaneously entraining planktonic prey1. These bands are strongly conserved across taxa spanning four major superphyla2,3, and they are responsible for the unusual morphologies of many invertebrate larvae4,5. However, few studies have investigated their underlying hydrodynamics6,7. Here, we study the ciliary bands of starfish larvae, and discover a beautiful pattern of slowly evolving vortices that surrounds the swimming animals. Closer inspection of the bands reveals unusual ciliary ‘tangles’ analogous to topological defects that break up and re-form as the animal adjusts its swimming stroke. Quantitative experiments and modelling demonstrate that these vortices create a physical trade-off between feeding and swimming in heterogeneous environments, which manifests as distinct flow patterns or ‘eigenstrokes’ representing each behaviour—potentially implicating neuronal control of cilia. This quantitative interplay between larval form and hydrodynamic function may generalize to other invertebrates with ciliary bands, and illustrates the potential effects of active boundary conditions in other biological and synthetic systems.
Similar content being viewed by others
Main
Many marine invertebrates develop in two stages, growing from swimming larvae to bottom-dwelling adults. This developmental dichotomy mandates physical trade-offs, resulting in a stunning variety of larval morphologies that have transfixed biologists and artists alike for more than a century8. Common to many larval forms are dense ciliary bands encircling the body, which propel the animal during escape and dispersal while also entraining motile plankton, their primary food source1. Ciliary bands are linear arrays of densely packed cilia, which form morphologies that are as diverse as the remarkable range of organisms in which they appear (which spans four major superphyla)3,9. Although several studies have emphasized the importance of ciliary bands in phylogenetic reconstruction2,9, few have quantitatively investigated them, particularly the physical mechanism by which they simultaneously maximize swimming flow while precisely capturing food particles—an intrinsic link between larval morphology and behaviour.
Here, we observe that the larva of the common starfish Patiria miniata generates around its body a beautiful and intricate array of counter-rotating vortices, which merge and split in a complex manner over time (Fig. 1a and Supplementary Movie 1; 29 larvae). We find these patterns in both freely swimming animals and animals held stationary, and the larvae swim irregularly as these currents evolve in time (Supplementary Movies 2–4; 37 larvae). Slowly varying vortices have been noted in several marine larvae, leading some authors to speculate that these structures play a crucial role in resolving the competing requirements of swimming and feeding1,4,5,7,10,11. Here we investigate this conjecture using a combination of live imaging and mathematical modelling, and we reveal a subtle interplay between organism-level band morphology and microscopic ciliary ‘tangles’, which jointly produce the distinctive, dynamic flow fields seen around the organism. We further analyse these flow fields to identify separate hydrodynamic ‘eigenstrokes’ corresponding to distinct feeding and swimming behaviours. To our knowledge, our results provide the first quantitative study of the relationship between form and function in ciliary bands, providing a biophysical example of how the competing hydrodynamics of feeding and swimming may unify morphology and behaviour in marine invertebrate development10.
a, An eight-week-old starfish larva feeds while held in a ∼0.5 mm gap between a glass slide and coverslip. Immobilization enables visualization of nine counter-rotating vortices by stacking 3 s sequences of a dark-field movie of 6 μm tracer particles39. Swimming direction upwards; scale bar, 350 μm. b, The frontal plane anatomy of a starfish larva, with the ciliary band highlighted as a dark line. Adapted from an 1877 lithograph ref. 8. c, A false-colour scanning electron micrograph highlighting the ciliary band (yellow). Scale bar, 20 μm.
Ciliary bands in a P. miniata larva surround the animal’s periphery, dividing the body into pre- and post-oral hoods and the circumoral field. Swimming occurs with the pre-oral hood facing upward and anterior facing forward1 (Fig. 1b). The circumoral bands are primarily responsible for the observed vortices, which localize to the animal’s midplane. The vortices remain mostly symmetric across the body axis (although this symmetry varies over time), and minor left–right differences in body morphology create small asymmetries in the vortex locations. The largest vortices occur at the posterior end of the larva, while smaller vortices localize to dense portions of the band near the side lobes. Stagnation points with zero net flow form where two counter-rotating vortices intersect. Consistent with previous larval feeding experiments6,7, algae that pass through the vortex field and contact the body surface are captured and then transported either along the ciliary band or by surface currents in the circumoral field until they reach the oral hood, where they aggregate before being ingested. An electron micrograph of a larva reveals shorter cilia covering the body surface that facilitate this transfer, with higher line densities of cilia (∼3 cilia μm−1) occurring along the ciliary band than on the body surface (<0.1 cilia μm−1)1,12 (Fig. 1c). This unusually high density and configuration of cilia enables physical interactions between the cilia of neighbouring cells, which is uncommon in single-cell ciliates13,14.
Closer inspection of the cilia reveals a typical stroke pattern (Fig. 2d and Supplementary Movie 14) with a mean beat frequency of 6 Hz and length of 30 μm, consistent with previous measurements1. These cilia create flow speeds of up to 300 μm s−1 tangential to the surface (and negligible flow through the surface), but which vary in magnitude and direction across the organism—giving rise to the observed vortices. Surprisingly, we observe unusual arrangements of the cilia wherever the surface beat direction reverses (Fig. 2), which we term ‘defects’ by analogy to topological defects observed in nematic liquid crystals and magnetic spins15. Cilia beating towards (away from) each other create outwards (inwards) flows and a characteristic tangle (splay) defect, hereafter denoted by + (−) (Supplementary Movies 5,13 and 25 larvae). The near-field streamlines match the predicted flow along a wall with a prescribed tangential flow velocity that undergoes a sudden change in sign (Fig. 2b). We image the defects and flow fields simultaneously, and we observe that each defect creates a boundary between two vortices of opposite rotation direction (Fig. 2c and Supplementary Movie 6). Consistent with the time-varying nature of larval swimming, defects can be seen to break up and re-form in place over timescales ∼10 s (Fig. 2e and Supplementary Movies 7 and 8), creating corresponding changes in the vortices. The defect locations appear to be determined anatomically, and typical locations for a larva are indicated in Fig. 2f.
a, Boundaries between vortices require local reversals in the surface beat direction of cilia, which create tangles (left, +) or splays (right, −) depending on the rotation directions of the vortices. b, Streamlines for a model flow generated by a sign change in the tangential velocity imposed on a surface, with the orientation of the cilia indicated schematically. c, Zoomed-out view of the same movie shown in a, with frames stacked over 4.5 s to show pathlines of advected particles near the defect. d, A trace of a typical ciliary stroke near a defect; colour code indicates evenly spaced time points (green to red). e, A kymograph of a tangle defect (with the locations of three representative cilia marked) with six movie frames called out. f, The locations of + and − defects on a typical larvae, with the locations in the previous panels indicated. Scale bars, 30 μm.
When motile algae (Rhodomonas lens, ∼ 6 μm) are added to seawater containing 0.75 μm beads, they appear to swim freely until they enter a high-speed (∼100 μm s−1) region near the body, where they are entrained and repeatedly swept towards the animal’s surface by surrounding vortices (Fig. 3a and Supplementary Movie 9). On approach to the body they may be captured through instantaneous reverse beats of single cilia (Fig. 3b and Supplementary Movie 10). This direct-capture mechanism has been reported in other marine plankton—including starfish—as a manifestation of ‘interception feeding’5,6,16. Hydrodynamically, vortex-mediated surface capture occurs due to short portions of the ciliary band beating in reverse relative to the direction of the prevailing swimming current1,4,7,17, which draw particles close to the surface for capture. These regions of the ciliary band span the region between two defects of opposite sign (Fig. 3c). The local structure of this mechanism is consistent across multiple animals; velocity line traces through the vortices overlap when rescaled by vortex speed and size (Fig. 3d), consistent with the power-law drop-off expected for a confined active swimmer18,19.
a, The flow field generated by a larva (blue) in a mixture of passive beads (light blue) and active algae (red). Movie frames stacked over 3 s; scale bar, 300 μm. b, A typical algae capture sequence, with the algae orientation indicated with an arrow. Scale bar, 40 μm. c, A schematic of local ciliary reversal between two defects capturing a particle, which is then passed along the surface by cilia. d, Line traces of the velocity component parallel to the body surface, taken through the largest vortex for eight organisms (a parabola is overlaid on the decay portions). e,f, Streamlines (e) and trajectories of incident algae particles (f) for the ‘two-mode’ squirmer for different orders n. Swimming (purple) and reversal (magenta) ciliary regions are indicated, and captured particle trajectories are highlighted in red. g, The swimming speed (purple) and capture cross-section (magenta) as a function of the number of vortices.
We incorporate these observations into a simple mathematical model that captures the trade-off between near-field feeding and the far-field swimming currents, which are both fully determined by the boundary condition imposed at the larvae’s surface. The flows are dominated by viscous rather than inertial forces (Re < 0.003), and so we adapt the classic ‘squirmer’ model for the propulsive currents generated by a two-dimensional, circular swimmer imposing an arbitrary tangential velocity profile along its surface—here representing the ciliary band outlining the frontal plane20. The velocity field around the swimmer is given by

where vr, vθ denote the radial and azimuthal velocity components in the co-moving frame, and a denotes the radius of the swimmer. The swimming speed is determined solely by the first-order mode, vswim = −(1/2)B1, because all other terms dependent on r vanish as r → ∞. The squirmer model has been successfully applied to single-celled organisms with localized thrust-generating appendages, which create ‘pusher/puller’ currents that manifest as a single pair of vortices at the fore/aft of the animal13,14. To our knowledge, ours is the first organism in which more than two such vortices are present, and so we introduce higher-order ‘squirming’ terms (Bn > 0; n > 2)—which we attribute to the more complex neurociliary control found in invertebrate larvae1,4.
We restrict ourselves to a set of ‘two-mode’ swimmers, each comprising a superposition of a swimming mode (B1) that generates propulsion via a streaming flow past the surface, and an ‘nth order’ mode (Bn, n ≥ 2) that has 2n sign changes (ciliary defects) along the surface that generate reversal regions (forming 2n − 2 vortices for n < 5, 2n vortices for n ≥ 5). Higher values of n result in smaller average distances between defects of opposite sign. Squirmers with different n are normalized by the maximum surface cilia beat speed and the size of the vortex region (the latter constraint is geometric rather than biological; see Supplementary Methods). Streamlines for n = 1,3,4 are shown in Fig. 3e, and the corresponding swimming speeds are observed to decrease with n (Fig. 3g, purple trace).
We introduce two-mode swimmers as a minimal model of locomotion with vorticity to quantify the effect of vortices on the feeding ability. In invertebrate zoology, the feeding rate (food particles per unit time) is typically estimated using the ‘clearance rate,’ or the volume of water searched by the animal per unit time7,16,21,22. This quantity has been investigated for a variety of marine larvae, and across many taxa it is generally found to increase with both the total ciliary band length and larval size1,12. Here we represent the total feeding rate  as the product of three factors,
as the product of three factors,

where ρ is the nutrient density, σ is the hydrodynamic capture cross-section (which may be larger than the animal’s body cross-section), and vswim is the swimming speed (which determines how often the animal encounters new food particles). The product σvswim is a volume flux that is equivalent to the clearance rate16,21,22,23. In previous clearance rate experiments conducted in homogeneous environments1,7, the feeding rate is maximized when the swimming speed vswim is maximized, as was found in recent theoretical work on osmotrophic feeders18,24. However, many zooplankton survive in extremely heterogeneous environments, in which their rate of feeding is not limited by their swimming speed but rather by their ability to encounter new microalgal patches and efficiently trap and capture food upon encounter23,25,26,27. In these circumstances, heterogeneity may encourage ‘cross-sectional feeding’ (maximizing σ) instead of ‘flux feeding’ (maximizing ρ vswim). This description matches findings for other model swimmers with feeding28, and it supports prior experimental observations1,7 that longer ciliary bands create a larger feeding rate even when they do not provide an increase in swimming speed12.
We estimate σ numerically by simulating the trajectory of a line source of particles incident on the squirmer, and probabilistically capture particles that pass within a fixed ‘interception distance’ of the surface (Supplementary Methods). For passive particles (as used in the simulations here), this is equivalent to determining the fraction of incoming streamlines that pass within the interception distance, weighted by their residence time. Example trajectories are shown in Fig. 3f, with those of captured particles highlighted in red. The number of captured particles is rescaled by the initial number of particles, the squirmer diameter, and the interception distance, to produce a non-dimensional cross-section that increases with increasing number of vortices (Fig. 3g). This increase arises primarily geometrically due to more particles being drawn into the interception region via streamline compression, as well as due to particles entering the interception region repeatedly and for longer times when more vortices are present—observations consistent with prior larval feeding experiments7. Adding random noise to the simulated particle trajectories to emulate algal diffusivity or activity further increases the capture cross-section (Supplementary Analysis).
The scaling of σ with n suggests a plausible reason for the striking flow fields observed around starfish larvae, for which additional vortices increase the feeding cross-section at the expense of the swimming speed. This trade-off is also consistent with the constraints of a fixed energy budget, since the swimmer either dissipates energy due to surface drag from swimming, or vortex core drag from feeding14,20. Our results also support previous evidence that organisms with finite interception/capture rates should favour vortical currents that draw particles near their surface16,27.
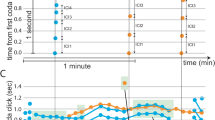
Next we investigate the temporal dynamics of the observed larval flow fields. Figure 4a shows three snapshots of the time-varying flow field around the organism, which changes dramatically over ∼10 s timescales (Supplementary Movie 11)—representing a known ‘arresting’ behaviour of starfish and other larvae in which short pauses punctuate regular swimming4,10,17 (Supplementary Movies 2 and 3). To quantify these flow field changes, particle image velocimetry (PIV) is used to extract the velocity field as a function of time29 (Supplementary Methods). Kymographs of the surface velocity profile illustrate that the flow transiently switches direction in the regions between two defects (Fig. 4b, d, boundaries between red/blue regions). This illustrates that the defects are dynamic, and it corroborates previous studies that report localized reversals of portions of the ciliary band1,4,7,17.
a, The flow fields generated by an eight-week-old larva at three different time points in a three-minute movie. The tangential velocity component along the surface is overlaid as a colour-coded outline on each image (pathline length: 9 s; scale bar, 500 μm). b, A kymograph of the magnitude of the tangential velocity component along the swimmer surface at all time points, with the top of the animal in the previous images vertically centred (darkest red, 292 μm s−1 clockwise; white, zero; darkest blue, 340 μm s−1 anticlockwise). c, The relative amplitudes of the first five terms of a least-squares fit of the squirmer model to each frame of the movie, with standard errors of the fit parameters indicated by shaded widths. The first-order ‘swimming’ mode corresponds to the magenta trace. The amplitudes of data projections onto the first two principal components are underlaid in grey. Blue boxes underlaid indicate when swimming or feeding dominate in the original movie. d, A surface velocity kymograph for the best-fit squirmer models from the previous panel e, Simulated flow fields for the best-fit squirmer model of the three movie frames shown in a, with the tangential velocity component colour-coded on the squirmer boundary.
Principal component analysis (PCA) applied to the entire velocity field time series reveals two principal components corresponding to distinct far-field swimming and near-field feeding vortex behaviours. Projecting each frame of the PIV data onto the two principal components reveals that the animal switches back and forth between the two modes (Fig. 4c, grey traces), consistent with the transitions seen in freely swimming animals4 (Supplementary Movie 2). Direct fitting to the individual modes of the squirmer model (Fig. 4c, coloured traces) confirms that the two anti-correlated principal components correspond to feeding and swimming: the first-order swimming mode (magenta trace) correlates with the first principal component, while the next four non-swimming modes resemble the anti-correlated component. These non-swimming modes lead to a higher capture cross-section when particle simulations are performed on each frame of the time series of best-fit squirmer models (Supplementary Analysis). Plots of the velocity field corresponding to each best-fit squirmer model (Fig. 4e) qualitatively resemble the original movie frames (Fig. 4a).
The correspondence of the PCA and squirmer fits suggest that larval behaviour is dominated by characteristic ‘eigenstrokes’—feeding and swimming—that can each be represented as amplitudes of a finite set of coefficients in the squirmer model. Low-dimensional behaviour has been observed in other living systems30,31,32; however, in our system these characteristic eigenmodes can be directly linked with both the governing physical equations (Stokes’ flow) and opposing biological functions (feeding and swimming). This behavioural switching may represent an adaptive strategy for heterogeneous environments, analogous to the ‘roaming/dwelling’ transition observed in other organisms that constitutes an optimal trade-off between global exploration and local exploitation33.
The complex spatiotemporal properties of the starfish larval flow field extend earlier results suggesting that the feeding/swimming dichotomy may be a fundamental design principle for marine invertebrate larvae5,10,34. Future field studies will further establish the relevance of the capture cross-section for the heterogeneous ocean environment, an open question in the literature on zooplankton grazing21,23,25. Additionally, in such a setting, vortex arrays may prove to have alternative functions, such as for masking mechanical strain fields that attract predators16. This would suggest that specific high-order power-law decay terms in the squirmer model may be favoured, constraining the placement and control of defects along the body.
Our work establishes a feeding/swimming trade-off exemplified by larvae such as echinoderms that use a single ciliary band to accomplish both functions. Future work will determine whether other planktonic larvae with different band morphologies (for example, opposed-band feeders, such as gastropod larvae) experience similar hydrodynamical constraints5. Importantly, single-band larvae rely on innervation to modulate separate functions within the band, leading some to speculate that the ciliary band preceded the evolution of the spinal cord2,4,35. Prior studies have indicated that the presence of MgCl2 in solution can inhibit larval muscle control and ciliary reversal1, causing the larvae to lose the ability to reverse direction after encountering obstacles (Supplementary Movie 15). This suggests the need for further work using pharmacological techniques to relate the dynamics of the ciliary defects to the nervous system. This will reveal whether the observed ciliary defects implicate previously identified neurociliary control mechanisms in invertebrate larvae4,11, and whether their locations arise from the finite axonal contact range of neurons responsible for ciliary control36.
Behaviour, adaptation and morphology in marine invertebrate larvae may be linked through the fluid mechanics of the ciliary band1,5,7. Our findings have additional potential implications for pathologies involving collective ciliary dyskinesia37. Moreover, it may also be possible to implement bioinspired ‘defect-driven’ boundary conditions in artificial systems as a means of stably generating complex flow structures38, with applications to soft robotics and impingement filtration22.
Data availability. The data that support the plots within this paper and other findings of this study are available from the corresponding author on request.
References
Strathmann, R. R. The feeding behavior of planktotrophic echinoderm larvae: mechanisms, regulation, and rates of suspension feeding. J. Exp. Mar. Biol. Ecol. 6, 109–160 (1971).
Nielsen, C. Structure and function of metazoan ciliary bands and their phylogenetic significance. Acta Zool. 68, 205–262 (1987).
Strathmann, R. R. Hypotheses on the origins of marine larvae. Ann. Rev. Ecol. Syst. 24, 89–117 (1993).
Lacalli, T., Gilmour, T. & West, J. Ciliary band innervation in the bipinnaria larva of Piaster ochraceus . Phil. Trans. R. Soc. Lond. B 330, 371–390 (1990).
von Dassow, G., Emlet, R. B. & Maslakova, S. A. How the pilidium larva feeds. Front. Zool. 10, 1 (2013).
Strathmann, R. R. Larval feeding in echinoderms. Am. Zool. 15, 717–730 (1975).
Hart, M. W. Particle captures and the method of suspension feeding by echinoderm larvae. Biol. Bull. 180, 12–27 (1991).
Agassiz, A. North American Starfishes Vol. 5 (Welch, Bigelow, and Company, University Press, 1877).
Amemiya, S. et al. Development of ciliary bands in larvae of the living isocrinid sea lily Metacrinus rotundus . Acta Zool. 96, 36–43 (2015).
Strathmann, R. R. & Grünbaum, D. Good eaters, poor swimmers: compromises in larval form. Integr. Comp. Biol. 46, 312–322 (2006).
Burke, R. D. The structure of the larval nervous system of Pisaster ochraceus (Echinodermata: Asteroidea). J. Morphol. 178, 23–35 (1983).
Hart, M. W. Variation in suspension feeding rates among larvae of some temperate, eastern Pacific echinoderms. Invert. Biol. 115, 30–45 (1996).
Goldstein, R. E. Green algae as model organisms for biological fluid dynamics. Ann. Rev. Fluid Mech. 47, 343 (2015).
Guasto, J. S., Rusconi, R. & Stocker, R. Fluid mechanics of planktonic microorganisms. Ann. Rev. Fluid Mech. 44, 373–400 (2012).
Chaikin, P. M. & Lubensky, T. C. Principles of Condensed Matter Physics Vol. 1 (Cambridge Univ. Press, 2000).
Kiørboe, T. How zooplankton feed: mechanisms, traits and trade-offs. Biol. Rev. 86, 311–339 (2011).
Mackie, G., Spencer, A. & Strathmann, R. Electrical activity associated with ciliary reversal in an echinoderm larva. Nature 223, 1384–1385 (1969).
Magar, V., Goto, T. & Pedley, T. Nutrient uptake by a self-propelled steady squirmer. Q. J. Mech. Appl. Math. 56, 65–91 (2003).
Pepper, R. E., Roper, M., Ryu, S., Matsudaira, P. & Stone, H. A. Nearby boundaries create eddies near microscopic filter feeders. J. R. Soc. Interface 7, 851–852 (2010).
Blake, J. Self propulsion due to oscillations on the surface of a cylinder at low Reynolds number. Bull. Aust. Math. Soc. 5, 255–264 (1971).
Rothschild, B. & Osborn, T. Small-scale turbulence and plankton contact rates. J. Plankton Res. 10, 465–474 (1988).
Rubenstein, D. I. & Koehl, M. The mechanisms of filter feeding: some theoretical considerations. Am. Nat. 111, 981–994 (1977).
Marrase, C., Costello, J. H., Granata, T. & Strickler, J. R. Grazing in a turbulent environment: energy dissipation, encounter rates, and efficacy of feeding currents in Centropages hamatus . Proc. Natl Acad. Sci. USA 87, 1653–1657 (1990).
Michelin, S. & Lauga, E. Optimal feeding is optimal swimming for all Péclet numbers. Phys. Fluids 23, 101901 (2011).
Fenchel, T. Microbial behavior in a heterogeneous world. Science 296, 1068–1071 (2002).
Siegel, D. A. Resource competition in a discrete environment: why are plankton distributions paradoxical? Limnol. Oceanogr. 43, 1133–1146 (1998).
Jiang, H., Osborn, T. R. & Meneveau, C. Chemoreception and the deformation of the active space in freely swimming copepods: a numerical study. J. Plankton Res. 24, 495–510 (2002).
Tam, D. & Hosoi, A. Optimal feeding and swimming gaits of biflagellated organisms. Proc. Natl Acad. Sci. USA 108, 1001–1006 (2011).
Taylor, Z. J., Gurka, R., Kopp, G. A. & Liberzon, A. Long-duration time-resolved PIV to study unsteady aerodynamics. IEEE Trans. Instrum. Meas. 59, 3262–3269 (2010).
Berman, G. J., Choi, D. M., Bialek, W. & Shaevitz, J. W. Mapping the stereotyped behaviour of freely moving fruit flies. J. R. Soc. Interface 11, 20140672 (2014).
Stephens, G. J., Johnson-Kerner, B., Bialek, W. & Ryu, W. S. Dimensionality and dynamics in the behavior of C. elegans . PLoS Comput. Biol. 4, e1000028 (2008).
Jordan, D., Kuehn, S., Katifori, E. & Leibler, S. Behavioral diversity in microbes and low-dimensional phenotypic spaces. Proc. Natl Acad. Sci. USA 110, 14018–14023 (2013).
Berg, H. C. Random Walks in Biology (Princeton Univ. Press, 1993).
Malkiel, E., Sheng, J., Katz, J. & Strickler, J. R. The three-dimensional flow field generated by a feeding calanoid copepod measured using digital holography. J. Exp. Biol. 206, 3657–3666 (2003).
Lowe, C. J., Clarke, D. N., Medeiros, D. M., Rokhsar, D. S. & Gerhart, J. The deuterostome context of chordate origins. Nature 520, 456–465 (2015).
Jékely, G. Origin and early evolution of neural circuits for the control of ciliary locomotion. Proc. R. Soc. B 278, 914–922 (2011).
Marshall, W. F. & Kintner, C. Cilia orientation and the fluid mechanics of development. Curr. Opin. Cell Biol. 20, 48–52 (2008).
Shields, A. et al. Biomimetic cilia arrays generate simultaneous pumping and mixing regimes. Proc. Natl Acad. Sci. USA 107, 15670–15675 (2010).
Gilpin, W. N., Prakash, V. & Prakash, M. Flowtrace: a simple visualization tool for biological fluid flows. Preprint at bioRxivhttp://dx.doi.org/10.1101/086140 (2016).
Acknowledgements
We thank C. Lowe, D. N. Clarke, K. Uhlinger, and Stanford BIOS 236; also R. Konte, L.-M. Joubert, M. S. Bull, D. Krishnamurthy, and the Prakash Laboratory. This work was supported by an ARO MURI Grant W911NF-15-1-0358 and an NSF CAREER Award (to M.P.) and an NSF GRFP DGE-114747 (to W.G.)
Author information
Authors and Affiliations
Contributions
All authors designed and planned research collaboratively and performed experiments. W.G. developed the theoretical model, and performed the numerical simulations and PIV analysis. All authors wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1831 kb)
Supplementary Movie 1
Supplementary Movie (MOV 68699 kb)
Supplementary Movie 2
Supplementary Movie (MOV 29895 kb)
Supplementary Movie 3
Supplementary Movie (MOV 3992 kb)
Supplementary Movie 4
Supplementary Movie (MOV 16567 kb)
Supplementary Movie 5
Supplementary Movie (MOV 6802 kb)
Supplementary Movie 6
Supplementary Movie (MOV 44784 kb)
Supplementary Movie 7
Supplementary Movie (MOV 6089 kb)
Supplementary Movie 8
Supplementary Movie (MOV 8960 kb)
Supplementary Movie 9
Supplementary Movie (MOV 1441 kb)
Supplementary Movie 10
Supplementary Movie (MOV 503 kb)
Supplementary Movie 11
Supplementary Movie (MOV 16595 kb)
Supplementary Movie 12
Supplementary Movie (MOV 1554 kb)
Supplementary Movie 13
Supplementary Movie (MOV 1683 kb)
Supplementary Movie 14
Supplementary Movie (MOV 4277 kb)
Supplementary Movie 15
Supplementary Movie (MOV 6339 kb)
Rights and permissions
About this article
Cite this article
Gilpin, W., Prakash, V. & Prakash, M. Vortex arrays and ciliary tangles underlie the feeding–swimming trade-off in starfish larvae. Nature Phys 13, 380–386 (2017). https://doi.org/10.1038/nphys3981
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3981
This article is cited by
-
Artificial-goosebump-driven microactuation
Nature Materials (2024)
-
Odd dynamics of living chiral crystals
Nature (2022)
-
Ultrasound-activated ciliary bands for microrobotic systems inspired by starfish
Nature Communications (2021)
-
Magnetic cilia carpets with programmable metachronal waves
Nature Communications (2020)
-
The multiscale physics of cilia and flagella
Nature Reviews Physics (2020)