Abstract
Although Weyl fermions have proven elusive in high-energy physics, their existence as emergent quasiparticles has been predicted in certain crystalline solids in which either inversion or time-reversal symmetry is broken1,2,3,4. Recently they have been observed in transition metal monopnictides (TMMPs) such as TaAs, a class of noncentrosymmetric materials that heretofore received only limited attention5,6,7. The question that arises now is whether these materials will exhibit novel, enhanced, or technologically applicable electronic properties. The TMMPs are polar metals, a rare subset of inversion-breaking crystals that would allow spontaneous polarization, were it not screened by conduction electrons8,9,10. Despite the absence of spontaneous polarization, polar metals can exhibit other signatures of inversion-symmetry breaking, most notably second-order nonlinear optical polarizability, χ(2), leading to phenomena such as optical rectification and second-harmonic generation (SHG). Here we report measurements of SHG that reveal a giant, anisotropic χ(2) in the TMMPs TaAs, TaP and NbAs. With the fundamental and second-harmonic fields oriented parallel to the polar axis, the value of χ(2) is larger by almost one order of magnitude than its value in the archetypal electro-optic materials GaAs11 and ZnTe12, and in fact larger than reported in any crystal to date.
Similar content being viewed by others
Main
The past decade has witnessed an explosion of research investigating the role of band-structure topology, as characterized for example by the Berry curvature in momentum space, in the electronic response functions of crystalline solids13. While the best established example is the intrinsic anomalous Hall effect in time-reversal breaking systems14, several nonlocal15,16 and nonlinear effects related to Berry curvature generally17,18 and in Weyl semimetals (WSMs) specifically19,20 have been predicted in crystals that break inversion symmetry. Of these, the most relevant to this work is a theoretical formulation21 of SHG in terms of the shift vector, which is a quantity related to the difference in Berry connection between two bands that participate in an optical transition.
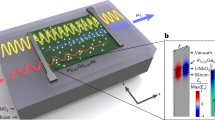
Figure 1a and its caption provide a schematic and description of the optical set-up for measurement of SHG in TMMP crystals. Figure 1b, c shows results from a (112) surface of TaAs. The SH intensity from this surface is very strong, allowing for polarization rotation scans with signal-to-noise ratio above 106. In contrast, SHG from a TaAs (001) surface is barely detectable (at least six orders of magnitude lower than the (112) surface). Below, we describe the use of the set-up shown in Fig. 1a to characterize the second-order optical susceptibility tensor, χijk, defined by the relation, Pi(2ω) = ε0χijk(2ω)Ej(ω)Ek(ω).
a, Schematic of the SHG experimental set-up. To stimulate second-harmonic light, pulses of 800 nm wavelength were focused at near-normal incidence to a 10-μm-diameter spot on the sample. Polarizers and waveplates mounted on rotating stages allowed for continuous and independent control of the polarization of the generating and second-harmonic light that reached the detector. θ1 and θ2 are the angles of the polarization plane after the generator and the analyser, respectively, with respect to the [1,1,−1] crystal axis. b,c, SHG intensity as a function of angle of incident polarization at 20 K. In b,c, the analyser is, respectively, parallel and perpendicular to the generator. In both plots the amplitude is normalized by the peak value in b. The solid lines are fits that include all the allowed tensor elements in 4mm symmetry, whereas the dashed lines include only d33. The insets are polar plots of measured SHG intensity versus incident polarization angle.
As a first step, we determined the orientation of the high-symmetry axes in the (112) surface, which are the [1,−1,0] and [1,1,−1] directions. To do so, we simultaneously rotated the linear polarization of the generating light (the generator) and the polarizer placed before the detector (the analyser), with their relative angle set at either 0° or 90°. Rotating the generator and analyser together produces scans, shown in Fig. 1b, c, which are equivalent to rotation of the sample about the surface normal. The angles at which we observe the peak and the null in Fig. 1b and the null in Fig. 1c allow us to identify the principal axes in the (112) plane of the surface.
Having determined the high-symmetry directions, we characterize χijk by performing three of types of scans, the results of which are shown in Fig. 2. In scans shown in Fig. 2a, b, we oriented the analyser along one of the two high-symmetry directions and rotated the plane of linear polarization of the generator through 360°. Figure 2c shows the circular dichroism of the SHG response—that is, the difference in SH generated by left and right circularly polarized light. For all three scans the SHG intensity as a function of angle is consistent with the second-order optical susceptibility tensor expected for the 4mm point group of TaAs, as indicated by the high accuracy of the fits in Fig. 1b, c and Fig. 2a–c.
a,b, SHG as function of generator polarization with analysers fixed along 0° (a) and 90° (b), which are the [1,1,−1] and [1,−1,0] crystal axes, respectively. Solid lines are fits considering all three non-zero tensor elements. The insets are polar plots of measured SHG intensity. c, Circular dichroism (SHG intensity difference between right- and left-hand circularly polarized generation light) normalized by the peak value in Fig. 1b versus polarization angle of the analyser at 300 K. The solid line is a fit. d, Temperature dependence of |d15/d33| and |d31/d33| of a TaAs (112) sample. The error bars are determined by setting d15 and d31 in phase and out of phase with respect to d33 in the fits.
In the 4mm structure xz and yz are mirror planes but reflection through the xy plane is not a symmetry; therefore, TaAs is an acentric crystal with an unique polar (z) axis. In crystals with 4mm symmetry there are three independent nonvanishing elements of χijk: χzzz, χzxx = χzyy and χxzx = χyzy = χxxz = χyyz. Note that each has at least one z component, implying null electric dipole SHG when all fields are in the xy plane. This is consistent with observation of nearly zero SHG for light incident on the (001) plane. Below, we follow the convention of using the 3 × 6 second-rank tensor dij, rather than χijk, to express the SHG response, where the relation between the two tensors for TaAs is: χzzz = 2d33, χzxx = 2d31 and χxzx = 2d15 (ref. 22) (see Methods and Supplementary Section A).
Starting with the symmetry-constrained d tensor, we derive expressions, specific to the (112) surface, for the angular scans with fixed analyser shown in Fig. 2a, b (Methods and Supplementary Section A). We obtain |deffcos2θ1 + 3d31 sin2θ1|2/27 and |d15|2 sin2(2θ1)/3 for analyser parallel to [1,1,−1] and [1,−1,0], respectively, where deff ≡ d33 + 2d31 + 4d15. Fits to these expressions yield two ratios: |deff/d15| and |deff/d31| . Although we do not determine |d33/d15| and |d33/d31| directly, it is clear from the extreme anisotropy of the angular scans that d33, which gives the SHG response when both generator and analyser are parallel to the polar axis, is much larger than the other two components. We can place bounds on |d33/d15| and |d33/d31| by setting d15 and d31 in and out of phase with d33. We note that the observation of circular dichroism in SHG, shown in Fig. 2c, indicates that relative phase between d15 and d33 is neither 0° or 180°, but rather closer to 30° (Supplementary Section A).
The results of this analysis are plotted in Fig. 2d, where it is shown that |d33/d15| falls in the range ∼25–33 for all temperatures, and |d33/d31| increases from ∼30 to ∼100 with increasing temperature. Perhaps because of its polar metal nature, the anisotropy of the second-order susceptibility in TaAs is exceptionally large compared with what has been observed previously in crystals with the same set of non-zero dij. For example, α-ZnS, CdS and KNiO3 have |d31| ≅ |d15| ≅d33/2 (ref. 23), while in BaTiO3 the relative sizes are reversed, with |d31| ≅ |d15| ≈ 2 |d33| (ref. 24).
Even more striking than the extreme anisotropy of χijk is the absolute size of the SHG response in TaAs. The search for materials with large second-harmonic optical susceptibility has been of continual interest since the early years of nonlinear optics25. To determine the absolute magnitude of the d coefficients in TaAs, we used GaAs and ZnTe as benchmark materials. Both crystals have large and well-characterized second-order optical response functions11,12, with GaAs regarded as having a SH susceptibility among the largest of any known crystal. GaAs and ZnTe are also ideal as benchmarks, because their response tensors have only one nonvanishing coefficient, d14 ≡ 1/2χxyz.
Figure 3a–c shows polar plots of SHG intensity as TaAs (112), ZnTe (110), and GaAs (111) are (effectively) rotated about the optic axis with the generator and analyser set at 0° and 90°. Also shown (as solid lines) are fits to the polar patterns obtained by rotating the χ(2) tensor to a set of axes that includes the surface normal, which is (110) and (111) for our ZnTe and GaAs crystals, respectively (Methods and Supplementary Section A). Even prior to analysis to extract the ratio of d coefficients between the various crystals, it is clear that the SHG response of TaAs (112) is large, as the peak intensity in this geometry exceeds ZnTe (110) by a factor of 4.0(±0.1) and GaAs (111) by a factor of 6.6(±0.1). Figure 3d compares the parallel polarization data for TaAs shown in Fig. 3a with SHG measured under the same conditions in the (112) facets of two other TMMPs: TaP and NbAs. The strength of SHG from the three crystals, which share the same 4mm point group, is clearly very similar, with TaP and NbAs intensities relative to TaAs of 0.90(±0.02) and 0.76(±0.04), respectively. The SHG response in these compounds is also dominated by the d33 coefficient. Finally, we found that the SHG intensity of all three compounds does not decrease after exposure to atmosphere for several months.
a–c, SHG polar plots in the same scale for TaAs (112) (a), ZnTe (110) (b) and GaAs (111) (c) in both the parallel and perpendicular generator/analyser configurations at room temperature. For TaAs, data in the perpendicular configuration is magnified by a factor of 4 for clarity. The SHG intensity of ZnTe and GaAs are multiplied by a factors of 4 and 6.6, respectively, to match the peak value of TaAs. d, SHG polar plots for TaAs (112), TaP (112) and NbAs (112) in the parallel configurations at room temperature, with plots of TaP and NbAs rotated by 60° and 120° for clarity.
To obtain the response of the TMMPs relative to the two benchmark materials we used the Bloembergen–Pershan formula25 to correct for the variation in specular reflection of SH light that results from the small differences in the index of refraction of the three materials at the fundamental and SH frequency. (See Methods. Details concerning this correction, which is less than 20%, can be found in Supplementary Section B.) Table 1 presents the results of this analysis, showing that |d33| ≅3,600 pm V−1 at the fundamental wavelength 800 nm in TaAs exceeds the values in the benchmark materials GaAs11 and ZnTe12 by approximately one order of magnitude, even when measured at wavelengths where their response is largest. The d coefficient in TaAs at 800 nm exceeds the corresponding values in the ferroelectric materials BiFeO3 (ref. 26), BaTiO3 (ref. 24) and LiNbO3 (ref. 23) by two orders of magnitude. In the case of the ferroelectric materials, SHG measurements have not been performed in their spectral regions of strong absorption, typically 3–7 eV. However, ab initio calculations consistently predict that the resonance-enhanced d values in this region do not exceed roughly 500 pm V−1 (refs 27,28).
The results described above raise the question of why χzzz in the TMMPs is so large. Answering this question quantitatively will require further work in which measurements of χ(2) as a function of frequency are compared with theory based on ab initio band structure and wavefunctions. For the present, we describe a calculation of χ(2) using a minimal model of a WSM that is based on the approach to nonlinear optics proposed by Morimoto and Nagaosa (MN)21. This theory clarifies the connection between band-structure topology and SHG, and provides a concise expression with clear geometrical meaning for χ(2). Hopefully this calculation will motivate the ab initio theory that is needed to quantitatively account for the large SH response of the TMMPs and its possible relation to the existence of Weyl nodes.
The MN result for the dominant (zzz) response function is

In equation (1) the nonlinear response is expressed as a second-order conductivity, σzzz(ω, 2ω), relating the current induced at 2ω to the square of the applied electric field at ω, that is, Jz(2ω) = σzzzEz2(ω). (The SH susceptibility is related to the conductivity through the relation χ(2) = σ(2)/2iωε0). The indices 1 and 2 refer to the valence and conduction bands, respectively, ε21 is the transition energy, and vi, 12 is the matrix element of the velocity operator vi = (1/ℏ)∂H/∂ki. Bandstructure topology appears in the form of the ‘shift vector,’ Rzz ≡ ∂kzφz, 12 + az, 1 − az, 2, which is a gauge-invariant length formed from the k derivative of the phase of the velocity matrix element, φ12 = Im{logv12}, and the difference in Berry connection, ai = −i〈un |∂ki| un〉, between bands 1 and 2. Physically, the shift vector is the k-resolved shift of the intracell wavefunction for the two bands connected by the optical transition.
We consider the following minimal model for a time-reversal symmetric WSM that supports four Weyl nodes,

Here, σi and si are Pauli matrices acting on the orbital and spin degrees of freedom, respectively, t is a measure of the bandwidth, a is the lattice constant, my and mz are parameters that introduce anisotropy, and inversion breaking is introduced by Δ. The Hamiltonian defined in equation (2) preserves two-fold rotation symmetry about the z-axis and the mirror symmetries Mx and My. These symmetries form a subset of the 4mm point group which is relevant to the optical properties of TMMPs.
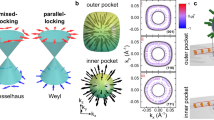
Figure 4 illustrates the energy levels, topological structure, and SHG spectra that emerge from this model. As shown in Fig. 4a, pairs of Weyl nodes with opposite chirality overlap at two points, k = (±π/2a, 0,0), in the inversion-symmetric case with Δ = 0. With increasing Δ the nodes displace in opposite directions along the ky axis, with Δky≅Δ/a. The energy of electronic states in the kz = 0 plane, illustrating the linear dispersion near the four Weyl points, is shown in Fig. 4b. Figure 4c shows the corresponding variation of |v12|2Rzz(k) for the sx = +1 bands whose Weyl points are located at ky < 0 (the variation of |v12|2Rzz(k) for the sx = −1 bands is obtained from the transformation k → − k). The magnitude of σ(2) derived from this model vanishes as Δ → 0, and is also sensitive to the anisotropy parameters my and mz. Figure 4d shows that spectra corresponding to parameters t = 0.8 eV, Δ = 0.5, mz = 5, and my = 1 can qualitatively reproduce the observed amplitude and large anisotropy of χ(2)(ω, 2ω).
a, Location of Weyl points in the kz = 0 plane for Δ = 0.5. For Δ = 0, Weyl points with opposite chiralities are located at (±π/2a,0,0) (denoted by black dots). b, The band structure for Δ = 0.5 and kz = 0. c, Colour plot of |v12|2Rzz, which appears as an integrand in the formula for σzzz(2). For clarity we plot only |v12|2Rzz for sx = +1 bands with Weyl points located at ky < 0. |v12|2Rzz for sx = −1 bands is obtained by setting k → −k. |v12|2Rzz shows structures at Weyl points. d, |χzzz| and |χxzx| plotted as a function of incident photon energy for Δ = 0.5. We adopted parameters t = 0.8 eV, my = 1, mz = 5.
As discussed above, our minimal model of an inversion-breaking WSM is intended mainly to motivate further research into the mechanism for enhanced SHG in the TMMPs. However, the model does suggest universal properties of χ(2) that arise from transitions near Weyl nodes between bands with nearly linear dispersion. According to bulk band-structure measurements7, such transitions are expected at energies below approximately 100 meV in the TaAs family, corresponding to the far-infrared and terahertz regimes. In these regimes, where the interband excitation is within the Weyl cones, the momentum-averaged |v12|2Rzz(k) tends to a non-zero value, 〈v2R〉, leading to the prediction that σ(2) → g(ω)〈v2R〉/ω2 as ω → 0. Because g(ω), the joint density of states for Weyl fermions, is proportional to ω2, we predict that σ(2) approaches a constant (or alternatively χ(2) diverges as 1/ω) as ω → 0, even as the linear optical conductivity vanishes in proportion to ω (ref. 29). The 1/ω scaling of SHG and optical rectification is a unique signature of a WSM in low-energy electrodynamics, as it requires the existence of both inversion breaking and point nodes. In real materials, this divergence will be cut off by disorder and non-zero Fermi energy. Disorder-induced broadening, estimated from transport scattering rates30, and Pauli blocking from non-zero Fermi energy, estimated from optical conductivity30 and band calculation3, each suggest a low-energy cutoff in the range of a few meV.
We conclude by observing that the search for inversion-breaking WSMs has led, fortuitously, to a new class of polar metals with unusually large second-order optical susceptibility. Although WSMs are not optimal for frequency-doubling applications in the visible regime because of their strong absorption, they are promising materials for terahertz generation and optoelectronic devices such as far-infrared detectors because of their unique scaling in the ω → 0 limit. Looking forward, we hope that our findings will stimulate further investigation of nonlinear optical spectra in inversion-breaking WSMs for technological applications and in order to identify the defining response functions of Weyl fermions in crystals.
Methods
Crystal growth and structure characterization.
Single crystals of TaAs, TaP and NbAs were grown by vapour transport with iodine as the transport agent. First, polycrystalline TaAs/TaP/NbAs was produced by mixing stoichiometric amounts of Ta/Nb and As/P and heating the mixture to 1,100/800/700 °C in an evacuated quartz ampule for two days. 500 mg of the resulting powder was then resealed in a quartz ampoule with 100 mg of iodine and loaded into a horizontal two-zone furnace. The temperatures of the hot and cold ends were held at 1,000 °C and 850 °C, respectively, for TaAs and 950 °C and 850 °C for TaP and NbAs. After four days, well-faceted crystals up to several millimetres in size were obtained. Crystal structure was confirmed using single-crystal X-ray micro-Laue diffraction at room temperature at beamline 12.3.2 at the Advanced Light Source.
Optics set-up for second-harmonic generation.
The optical set-up for measuring SHG is illustrated in Fig. 1a. Generator pulses of 100 fs duration and centre wavelength 800 nm pass through a mechanical chopper that provides amplitude modulation at 1 kHz and are focused at near-normal incidence onto the sample. Polarizers and waveplates in the beam path are used to vary the direction of linear polarization and to generate circular polarization. Both the specularly reflected fundamental and the second-harmonic beam are collected by a pickoff mirror and directed to a short-pass, band-pass filter combination that allows only the second-harmonic light to reach the photomultiplier tube (PMT) photodetector. Another wire-grid polarizer placed before the PMT allows for analysis of the polarization of the second-harmonic beam. Temperature-dependence measurements were performed by mounting the TaAs sample in a cold-finger cryostat on an xyz-micrometer stage. Benchmark measurements on TaAs, TaP, NbAs, ZnTe and GaAs were performed at room temperature in atmosphere with the samples mounted on an xyz-micrometer stage to maximize the signal.
Calculation and fitting procedure for SHG.
In noncentrosymmetric materials the second-order term, Pi(2) = ε0χijkEjEk, which gives rise to SHG and optical rectification, is allowed31,32. These two phenomena arise from excitation with a single frequency; therefore, there is an automatic symmetry with respect to permutation of the second and third indices in χijk. This motivates the use of a 3 × 6 second-rank tensor dij instead of χijk, and the former is more often used in SHG. The relation between dij and χijk is as follows: the first index i = 1,2,3 in dij corresponds to i′ = x, y, z, respectively, in χi′j′k′ and the second index j = 1,2,3,4,5,6 in dij corresponds to j′k′ = xx, yy, zz, yz/zy, zx/xz, xy/yx in χi′j′k′. Further discussion is provided in the Supplementary Information.
To fit the SHG polar pattern of TMMPs, we first fit data obtained with a fixed analyser at 90°, which is the [1,−1,0] crystal axis, because there is only one free parameter (|d15|) in this configuration:

With this value for |d15|, we then fit data in the three other types of scans discussed in the text, with d15 and d31 set in and out of phase with d33. The angular dependences in the parallel and perpendicular configurations are


When the analyser is fixed along 0°, the angular dependence is

This procedure yields upper and lower bounds on the anisotropy ratios |d15/d33| and |d31/d33|, which are shown with error bars in Fig. 2d.
In the circular dichroism experiment, to lowest order in dij, the angular dependence is

In the case of GaAs and ZnTe, all scans are fitted accurately by the only symmetry-allowed free parameter, |d14| . The angular dependences for ZnTe (110) in the parallel and perpendicular configurations are


The angular dependences for GaAs (111) in the parallel and perpendicular configurations are


See Supplementary Information for a full derivation.
Bloembergen–Pershan correction.
When measuring in the reflection geometry, one needs to consider the boundary condition to calculate χ(2) from χR(2), which was directly measured, where ‘R’ stands for reflection geometry. The correction was worked out by Bloembergen–Pershan (BP)33:

where ε is the relative dielectric constant and T(ω) = (2/(n(ω) + 1)) is the Fresnel coefficient of the fundamental light. In the current experiment, performed at 800 nm, the BP correction is fairly small (less than 20%). See Supplementary Information for more details.
Data availability.
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Burkov, A. & Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107, 127205 (2011).
Weng, H., Fang, C., Fang, Z., Bernevig, B. A. & Dai, X. Weyl semimetal phase in noncentrosymmetric transitionmetal monophosphides. Phys. Rev. X 5, 011029 (2015).
Huang, S.-M. et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 6, 7373 (2015).
Xu, S.-Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Lv, B. et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015).
Yang, L. et al. Weyl semimetal phase in the noncentrosymmetric compound TaAs. Nat. Phys. 11, 728–732 (2015).
Anderson, P. & Blount, E. Symmetry considerations on martensitic transformations: “ferroelectric” metals? Phys. Rev. Lett. 14, 217 (1965).
Shi, Y. et al. A ferroelectric-like structural transition in a metal. Nat. Mater. 12, 1024–1027 (2013).
Kim, T. et al. Polar metals by geometric design. Nature 533, 68–72 (2016).
Bergfeld, S. & Daum, W. Second-harmonic generation in GaAs: experiment versus theoretical predictions of χ xyz(2) . Phys. Rev. Lett. 90, 036801 (2003).
Wagner, H. P., Kuhnelt, M., Langbein, W. & Hvam, W. Dispersion of the second-order nonlinear susceptibility in ZnTe, ZnSe, and ZnS. Phys. Rev. B 58, 10494 (1998).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959 (2010).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1939 (2010).
Orenstein, J. & Moore, J. E. Berry phase mechanism for optical gyrotropy in stripe-ordered cuprates. Phys. Rev. B 87, 165110 (2013).
Zhong, S., Orenstein, J. & Moore, J. E. Optical gyrotropy from axion electrodynamics in momentum space. Phys. Rev. Lett. 115, 117403 (2015).
Moore, J. E. & Orenstein, J. Confinement-induced Berry phase and helicity-dependent photocurrents. Phys. Rev. Lett. 105, 165110 (2010).
Sodemann, I. & Fu, L. Quantum nonlinear Hall effect induced by Berry curvature dipole in time-reversal invariant materials. Phys. Rev. Lett. 115, 216806 (2015).
Ishizuka, H., Hayata, T., Ueda, M. & Nagaosa, N. Emergent electromagnetic induction and adiabatic charge pumping in Weyl semimetals. Preprint at http://arXiv.org/abs/1607.06537 (2016).
Chan, C.-K., Lindner, N. H., Refael, G. & Lee, P. A. Photocurrents in Weyl semimetals. Preprint at http://arXiv.org/abs/1607.07839 (2016).
Morimoto, T. & Nagaosa, N. Topological nature of nonlinear optical effects in solids. Sci. Adv. 2, 1501524 (2016).
Boyd, R. W. Nonlinear Optics (Academic, 2003).
Shoji, I., Kondo, T., Kitamoto, A., Shirane, M. & Ito, R. Absolute scale of second-order nonlinear-optical coefficients. JOSA B 14, 2268–2294 (1997).
Miller, R. C. Optical harmonic generation in single crystal BaTiO3 . Phys. Rev. 134, A1313 (1964).
Bloembergen, N. & Pershan, P. Light waves at the boundary of nonlinear media. Phys. Rev. 128, 606 (1962).
Haislmaier, R. C. et al. Large nonlinear optical coefficients in pseudo-tetragonal BiFeO3 thin films. Appl. Phys. Lett. 103, 031906 (2013).
Ju, S., Cai, T.-Y. & Guo, G.-Y. Electronic structure, linear, and nonlinear optical responses in magnetoelectric multiferroic material BiFeO3 . J. Chem. Phys. 130, 214708 (2009).
Young, S. M. & Rappe, A. M. First principles calculation of the shift current photovoltaic effect in ferroelectrics. Phys. Rev. Lett. 109, 116601 (2012).
Hosur, P., Parameswaran, S. & Vishwanath, A. Charge transport in Weyl semimetals. Phys. Rev. Lett. 108, 046602 (2012).
Xu, B. et al. Optical spectroscopy of the Weyl semimetal TaAs. Phys. Rev. B. 93, 121110, (2016).
Boyd, R. W. Nonlinear Optics (Academic, 2003).
Shen, Y.-R. Principles of Nonlinear Optics (Wiley-Interscience, 1984).
Bloembergen, N. & Pershan, P. Light waves at the boundary of nonlinear media. Phys. Rev. 128, 606 (1962).
Acknowledgements
We thank B. M. Fregoso, T. R. Gordillo, J. Neaton and Y. R. Shen for helpful discussions and B. Xu for sharing refractive index data of TaAs. Measurements and modelling were performed at the Lawrence Berkeley National Laboratory in the Quantum Materials program supported by the Director, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division, of the US Department of Energy under Contract No. DE-AC02-05CH11231. J.O., L.W. and A.L. received support for performing and analysing optical measurements from the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant GBMF4537 to J.O. at UC Berkeley. Sample growth was supported by the Gordon and Betty Moore Foundation’s EPiQS Initiative Grant GBMF4374 to J.A. at UC Berkeley. T.M. is supported by the Gordon and Betty Moore Foundation’s EPiQS Initiative Theory Center Grant GBMF4307 to UC Berkeley. J.E.M. received support for travel from the Simons Foundation. The authors would like to thank Nobumichi Tamura for his help in performing crystal diffraction and orientation on beamline 12.3.2 at the Advanced Light Source. N. Tamura and the ALS are supported by the Director, Office of Science, Office of Basic Energy Sciences, of the US Department of Energy under Contract No. DE-AC02-05CH11231. J. A. and N. N. acknowledge support by the Office of Naval Research under the Electrical Sensors and Network Research Division, Award No. N00014-15-1-2674.
Author information
Authors and Affiliations
Contributions
L.W. and J.O. conceived the project. L.W. and S.P. performed and contributed equally to the SHG measurements with assistance from E.T. and A.L. L.W. and J.O. analysed the data. T.M. and J.E.M. performed the model calculation. L.W., T.M. and J.O. performed the frequency scaling analysis. N.L.N. and J.G.A. grew the crystals and characterized the crystal structure. L.W., T.M. and J.O. wrote the manuscript. All authors commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 217 kb)
Rights and permissions
About this article
Cite this article
Wu, L., Patankar, S., Morimoto, T. et al. Giant anisotropic nonlinear optical response in transition metal monopnictide Weyl semimetals. Nature Phys 13, 350–355 (2017). https://doi.org/10.1038/nphys3969
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3969
This article is cited by
-
Surface-dominated conductance scaling in Weyl semimetal NbAs
npj Computational Materials (2024)
-
Three-dimensional nonlinear optical materials from twisted two-dimensional van der Waals interfaces
Nature Photonics (2024)
-
Optical second harmonic generation in anisotropic multilayers with complete multireflection of linear and nonlinear waves using ♯SHAARP.ml package
npj Computational Materials (2024)
-
Electric quadrupole second-harmonic generation revealing dual magnetic orders in a magnetic Weyl semimetal
Nature Photonics (2024)
-
Magneto-optical conductivity of threefold Hopf semimetals
Journal of the Korean Physical Society (2024)