Abstract
High-harmonic generation (HHG) in bulk solids permits the exploration of materials in a new regime of strong fields and attosecond timescales1,2,3,4,5,6. The generation process has been discussed in the context of strongly driven electron dynamics in single-particle bands7,8,9,10,11,12,13,14. Two-dimensional materials exhibit distinctive electronic properties compared to the bulk that could significantly modify the HHG process15,16, including different symmetries17,18,19, access to individual valleys20,21 and enhanced many-body interactions22,23,24,25. Here we demonstrate non-perturbative HHG from a monolayer MoS2 crystal, with even and odd harmonics extending to the 13th order. The even orders are predominantly polarized perpendicular to the pump and are compatible with the anomalous transverse intraband current arising from the material’s Berry curvature, while the weak parallel component suggests the importance of interband transitions. The odd harmonics exhibit a significant enhancement in efficiency per layer compared to the bulk, which is attributed to correlation effects. The combination of strong many-body Coulomb interactions and widely tunable electronic properties in two-dimensional materials offers a new platform for attosecond physics.
Similar content being viewed by others
Main
The recent observation of HHG in bulk solids provides a new approach to attosecond photonics and has opened up exciting opportunities for the study of strong-field and ultrafast electron dynamics in the condensed phase1,2,3,4,5,6. HHG has been observed from various crystals, including ZnO1,4, GaSe2,5, SiO2 (ref. 3), and the rare-gas solids of Ar and Kr (ref. 6). Several theoretical models have been proposed for bulk HHG in terms of intra- and interband electron dynamics1,2,3,4,5,6,7,8,9,10,11,12,13,14; however, the underlying mechanism for HHG is still under debate, and a unified predictive theory that captures the diversity of solids remains elusive. Notably, it is not yet clear to what extent electron correlation affects the generation process. In the case of rare-gas solids, a second plateau is observed beyond the atomic limit6. Although multiple plateaux can be explained within a single-particle picture6,13, the position of the second plateau at twice the exciton energy suggests the importance of correlation effects in HHG processes in these solids. Such many-body effects are greatly enhanced in atomically thin layers, as exemplified by the observation of strongly bound excitons in monolayer transition metal dichalcogenides (TMDCs)22,23,24,25. In addition to strong electronic correlations, the valley-contrasting Berry curvature resulting from the broken inversion symmetry in the monolayers20,21,26 could give rise to the generation of even harmonics from intraband currents1. Motivated by these distinctive properties of monolayer TMDCs, we have investigated the HHG from monolayer MoS2 crystals.
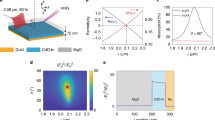
Monolayer MoS2 is composed of two hexagonal layers of S atoms surrounding a central hexagonal layer of Mo atoms with trigonal prismatic coordination (inset of Fig. 1). Unlike the bulk crystal, with its bilayer unit cell, the monolayer breaks inversion symmetry. In our experiment, we probed HHG from a monolayer MoS2 crystal prepared on a fused silica substrate. We excited the sample at normal incidence with ∼160 fs mid-infrared pulses at a photon energy of 0.30 eV, well below the direct bandgap around 1.8 eV. Linearly polarized pump pulses with intensity up to 2.5 TW cm−2 at a 1 kHz repetition rate were applied to the sample without noticeable damage. Figure 1 shows a representative high harmonic (HH) spectrum from a monolayer MoS2 crystal at a peak applied intensity of 2.2 TW cm−2. The field inside the monolayer is estimated at 0.33 V Å−1, taking into account the reflectivity of the substrate. At this field strength the laser imparts momentum to the electrons of magnitude comparable to the size of the Brillouin zone within a half laser cycle. Here the spectrum exhibits distinct peaks at integer multiples of the pump photon energy, corresponding to the 6th to 13th harmonic, above the direct bandgap. Both even and odd harmonics are present. The reported spectral range was defined by our detection scheme (see Methods for details). As we reduce the pump intensity, the strength of the harmonics decreases monotonically to the experimental noise level; we do not observe an abrupt cutoff for the generation of different harmonics.
We measured the HH yield as a function of pump intensity I (Fig. 2). A power-law fit to the data yields an intensity dependence of I3.3 for all orders (solid lines in Fig. 2). This result establishes the non-perturbative character of the generation process; in the perturbative limit, we would expect the hth harmonic yield to scale as the Ih (dashed lines in Fig. 2).
The measured harmonic yield as a function of the peak pump intensity I for representative harmonic orders h = 7, 9, 12 and 13 (dots). A fit of the experimental data to a power law, Ip, yields a phenomenological exponent of p = 3.3 for all four harmonic orders (solid lines). This behaviour deviates strongly from the behaviour for a perturbative nonlinear response of p = h (dashed lines, scaled to experiment at the highest intensity).
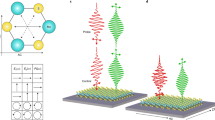
The role of crystal symmetry in the nonlinear optical response of monolayer MoS2 has been well established in the perturbative regime17,18,19. Here we characterize the non-perturbative HHG from the monolayer in the context of crystal symmetry using a linearly polarized pump. The dependence on ellipticity is given in the Supplementary Information. We analyse the polarization components of the HH radiation, perpendicular and parallel to the linearly polarized fundamental field, as a function of crystal orientation (Fig. 3a, d). Figure 3b shows a false colour representation of the HH spectrum in the perpendicular configuration as a function of the angle θ between the pump polarization and the mirror plane of the crystal (Fig. 3a). The signal is dominated by the even orders (8th, 10th and 12th). The integrated harmonic yields of these orders are presented in Fig. 3c. As functions of the crystal orientation, the intensities of the even harmonics are strongly modulated with a common period of 60°. The modulation of the various harmonics is in phase, and the modulation depths are near unity. When the mirror plane is parallel to the fundamental polarization (θ = 0°, 60°, 120°, …), mirror symmetry requires the induced even harmonic current (and thus the corresponding harmonic radiation) perpendicular to the fundamental field to vanish. By symmetry, the perpendicular components of the odd harmonics are also required to vanish for excitation parallel to the mirror plane. The observed lack of perpendicularly polarized odd harmonics for all crystal orientations is consistent with this prediction.
a, Experimental arrangement for the perpendicular polarization configuration. The red and blue arrows represent the fundamental and the harmonic fields, respectively. The dashed line identifies the (perpendicular) mirror symmetry plane of the crystal, and θ denotes the relative angle between the mirror plane and the fundamental field. b, False colour representation of the HHG spectrum versus crystal orientation in the perpendicular polarization configuration. The colour bar represents the measured harmonic yield on a linear scale. c, Normalized HH intensities for the perpendicular configuration, obtained by integrating the corresponding spectral regions in b. The coloured stripes provide a scale from 0 to 1 for each order. d–f, are the same as a–c, except that the parallel HH component is measured. The strength of the 8th harmonic in f is comparable to the noise level and has been omitted.
In the parallel configuration, both odd and even harmonics are detected (Fig. 3e, f). Similar to the perpendicular configuration, the even orders exhibit a near-unity depth of modulation, with six-fold rotational periodicity. Their intensity extrema are, however, shifted by 30° in θ compared to the corresponding perpendicular component. The vanishing parallel component of the even harmonics when the fundamental field is perpendicular to the mirror plane is again a consequence of symmetry. In contrast, the parallel components of the odd harmonics are not subject to such symmetry requirements; in general, they are observed for all crystal orientations (Fig. 3f), albeit with increasing orientation dependence for increasing harmonic order. A table summarizing the symmetry selection rules described above is provided in the Supplementary Information.
Non-perturbative HHG in bulk solids originates from coupled intraband and interband contributions to the nonlinear current1,2,3,4,5,7,8,9,10,11,12,13,14. The intraband contribution reflects nonlinear currents from non-parabolic band dispersion, whereas the interband contribution arises from an induced polarization between valence and conduction bands. The presence of even harmonics in ZnO was attributed to a finite Berry phase1, whereas, for GaSe, multiband interference was evoked5. To gain insight into the problem, we provide a simple and intuitive model based on semiclassical dynamics within a single band that qualitatively captures the main features of our measurement. The validity of this model requires that the electron traverses a large fraction of the Brillouin zone on a timescale that is short compared to interband transitions—that is, that the Bloch frequency is large compared to the relevant Rabi frequency. In this model, a small fraction of the electrons are assumed to tunnel from the valence band to the conduction band near the direct gap at the peak of the pump field. The electrons and holes are subsequently accelerated in their respective bands by the driving pulse. In this limit, we show that the semiclassical equations for the intraband current, when the Berry curvature term has been included, can lead to the production of both odd and even harmonics polarized respectively parallel and perpendicular to the drive field.
The semiclassical equations of motion for carriers within a single-particle band are


where r is the position of an electron wave packet, k is its wave vector, E is the electric field of the applied optical radiation inside the crystal, and ɛ and Ω are, respectively, the energy and Berry curvature20,26 of the conduction (or valence) band. We have neglected the Lorentz force term in equation (1), which can only contribute to the production of even harmonics through an in-plane current with an out-of-plane magnetic field component, and is thus absent for the normal incidence geometry used here. In this model, we also omit scattering, which may be of secondary importance given the high field strength and short timescale of the processes under consideration. Equations (1) and (2) are valid when the transition rate is small compared to the relevant band separations26. The HH nonlinear current within this model is directly proportional to the group velocity of the electron packet,  .
.
The perpendicular component of the even harmonics is seen to dominate in our experiment. This result is consistent with the anomalous currents driven by the Berry curvature term in equation (2). The effect of this term is to introduce an anomalous in-plane current j⊥(t) that is perpendicular to the driving field, since  is parallel to E (by equation (1)) and Ω is perpendicular to the plane of the crystal. In this sense, the Berry curvature acts like an artificial out-of-plane magnetic field. To understand the role of this term, we must take into account both the symmetry of the Berry curvature, which has the same magnitude but opposite sign for k and −k, and the fact that the electrons sample a large region of reciprocal space. The former gives rise to well-defined selection rules for the degenerate K and K′ valleys20. Consider an electron density N distributed equally between the K and K′ valleys at the peak of the applied field. Since the Berry curvature has opposite signs in the two valleys20, when the driving field is, for example, parallel to the mirror plane the contributions from intraband motion for
is parallel to E (by equation (1)) and Ω is perpendicular to the plane of the crystal. In this sense, the Berry curvature acts like an artificial out-of-plane magnetic field. To understand the role of this term, we must take into account both the symmetry of the Berry curvature, which has the same magnitude but opposite sign for k and −k, and the fact that the electrons sample a large region of reciprocal space. The former gives rise to well-defined selection rules for the degenerate K and K′ valleys20. Consider an electron density N distributed equally between the K and K′ valleys at the peak of the applied field. Since the Berry curvature has opposite signs in the two valleys20, when the driving field is, for example, parallel to the mirror plane the contributions from intraband motion for  along the K–K and K′–K′ directions will cancel one another, and j⊥(t) will vanish. As a result, no even harmonics are allowed in this configuration, in agreement with our measurements (Fig. 3b, c).
along the K–K and K′–K′ directions will cancel one another, and j⊥(t) will vanish. As a result, no even harmonics are allowed in this configuration, in agreement with our measurements (Fig. 3b, c).
On the other hand, when the driving field is perpendicular to the mirror plane—that is, when  is along the K–K′ and K′–K directions—the even harmonics (h = 2s) perpendicular to the driving field from the Berry curvature term do not cancel, consistent with our measurements. In this case, the anomalous perpendicular current from (2) is given by
is along the K–K′ and K′–K directions—the even harmonics (h = 2s) perpendicular to the driving field from the Berry curvature term do not cancel, consistent with our measurements. In this case, the anomalous perpendicular current from (2) is given by

where Ωn, N, e, ωB = eEd/ℏ, d = a/2, J2s are, respectively, the nth (sine) Fourier coefficient of the Berry curvature, the total electron density, the electron charge, the Bloch frequency, half of the lattice constant, and Bessel functions of the first kind. (See Supplementary Information for details.) The nonlinearity in this model is contained in the Bessel function and shows non-perturbative behaviour when nωB > ω (corresponding to a non-negligible spatial Fourier component Ωn).
In this scenario, the nonlinear current related to the band dispersion (the first term in equation (2)) is parallel to the electric field, which results in periodically modulated Bloch oscillations and is given by (see Supplementary Information)

where ɛn is the nth Fourier (cosine) coefficient of the conduction band. Equation (4) gives rise only to odd harmonics (h = 2s − 1) along the direction of the fundamental polarization1,3,7. This response could, in principle, explain the increasing modulation depth of odd harmonics as the harmonic order is increased. In this model, the sensitivity to orientation of the odd harmonic can be attributed to the non-parabolic and anisotropic nature of the band dispersion. This manifests itself primarily for the higher harmonics, where contributions from higher Fourier components of the band are more important. In the non-perturbative regime, the even harmonics are comparable to neighbouring odd harmonics when the dimensionless parameter 2sℏω Ωn/ɛnn2d2 is of order unity. This criterion is easily satisfied for our conditions, with Ω ∼ 10 Å2, ɛ ∼ few eV, d ∼ 1.6 Å (see Supplementary Information). A calculation of HHG intensity based on Equations (3) and (4) is given in the Supplementary Information.
The model described above gives a simple, intuitive picture of how the broken inversion symmetry could give rise to perpendicularly polarized even harmonics in the strong-field limit. Within this picture, however, the presence of a nonzero component polarized parallel to the pump demonstrates that interband transitions must also contribute to the generation process. The need to include the interband response beyond tunnelling is not surprising, given that the optical properties of the monolayer are strongly influenced by excitonic effects.
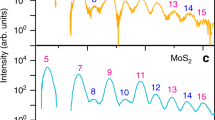
To test whether the reduced dimensionality of the monolayer plays an important role in the HHG process, we compare the relative harmonic efficiency from monolayer MoS2 to that from a corresponding layer of the bulk MoS2 crystal. In doing so, we account for the linear optical propagation effects present in our measurement of the bulk crystal, including reflections of the excitation pulse and the absorption of the HH radiation, by applying standard transfer-matrix methods. (See Supplementary Information.) The resulting relative HHG efficiencies for the isolated monolayer and an effective monolayer in the bulk are shown in Fig. 4. Whereas strong even harmonics are observed from the isolated monolayers, they are completely absent in the HHG spectrum from the bulk. As discussed above, the emergence of even harmonics in monolayers is a consequence of its broken inversion symmetry, in contrast to the centrosymmetric bulk. The harmonic yields of the monolayer and bulk crystal used to obtain Fig. 4 are presented in the Supplementary Information.
In addition to the emergence of even harmonics, another key distinction of HHG from the monolayer is that the generation of odd HHs is significantly more efficient compared to that from an equivalent layer in the bulk. To understand this difference, we consider the electronic properties of the monolayer and its bulk counterpart. Increased quantum confinement in the monolayer compared to the bulk causes an increase in the indirect optical bandgap energy by ∼0.5 eV, whereas the direct optical bandgap remains nearly unchanged in energy27,28. Enhancement in the HHG efficiency within an intraband picture would require the Fourier components of the valence or conduction bands to be altered to exhibit much stronger band dispersion than in the bulk, contrary to what is expected28,29. Yet, there is another important distinction between the monolayer and the bulk: charge carriers in isolated monolayer MoS2 experience greatly enhanced electron–hole Coulomb interactions. This is a consequence of reduced dielectric screening in the monolayer22,23,24. The enhanced electron–hole interactions would lead to an enhanced oscillator strength from strongly bound excitons (and thus an increased Rabi frequency), as well as an increase in the probability of electron–hole recollision, analogous to the electron–ion recollision that accounts for the HHG in atoms.
The enhanced HHG efficiency from the isolated monolayer suggests that the strong Coulomb interaction between electrons and holes is important in the HHG process. To further elucidate the role of correlation effects, experiments could be designed to measure HHG spectra of atomically thin materials in which the strength of Coulomb interactions was tuned by doping or substrate effects. More generally, the observation of HHG from atomically thin semiconductors demonstrates the ability to study strong-field and attosecond phenomena in materials of reduced dimensionality. This could lead to a new level of control by experimentally tuning the electronic properties of an atomically thin sample, for example, by optical or electrostatic gating, strain, or layer stacking. Finally, we note that similar to recent efforts to recover band structure based on solid-state HHG3,30, our work suggests the possibility, under appropriate conditions, of all-optical measurement of the Berry curvature in materials that lack inversion symmetry.
Methods
To generate the HHs, pump pulses were obtained by difference-frequency mixing of the signal and idler outputs of a Ti:sapphire pumped optical parametric amplifier, operating at a 1 kHz repetition rate. The signal and idler had pulse energies of 325 μJ and 175 μJ and were centred at photon energies of 0.92 eV and 0.62 eV, respectively. The difference frequency of the signal and idler beams was produced in a 1-mm-thick AgGaS2 crystal, which yielded 160-fs pump pulses centred at 0.30 eV. The pump pulses were focused by a reflective objective (40×, NA = 0.5) to a spot size of 8 μm on a single-crystal domain of monolayer MoS2 supported on a fused silica substrate. The MoS2 monolayers were prepared by chemical vapour deposition. (Slabs of the bulk crystal of approximately 60-nm thickness were also prepared by exfoliation for the comparative studies.) A white-light source was coupled to the spectroscopy system for simultaneous imaging of the sample.
The HH radiation was collected in a transmission geometry by a second reflective objective (40×, NA = 0.5), which focused the radiation onto the entrance slit of a spectrometer. The HH spectra were collected by a thermoelectrically cooled Si charge-coupled devive (CCD) detector. The diffraction grating was blazed for 500 nm and had low efficiency for photon energies above 4 eV, defining the highest photon energy observed in the spectra of Fig. 1. The grating response for different polarizations was characterized by applying a white-light source spanning the HHG spectral range. In studying the crystal orientation dependence of the HHG process, we kept the sample orientation fixed while simultaneously changing the polarizations of the pump and detected harmonic radiation. The fundamental polarization was controlled by a MgF2 half-wave plate before the sample. An analyser after the sample selected the parallel or perpendicular components of the harmonic radiation.
Data availability.
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Ghimire, S. et al. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 7, 138–141 (2011).
Schubert, O. et al. Sub-cycle control of terahertz high-harmonic generation by dynamical Bloch oscillations. Nat. Photon. 8, 119–123 (2014).
Luu, T. T. et al. Extreme ultraviolet high-harmonic spectroscopy of solids. Nature 521, 498–502 (2015).
Vampa, G. et al. Linking high harmonics from gases and solids. Nature 522, 462–464 (2015).
Hohenleutner, M. et al. Real-time observation of interfering crystal electrons in high-harmonic generation. Nature 523, 572–575 (2015).
Ndabashimiye, G. et al. Solid-state harmonics beyond the atomic limit. Nature 534, 520–523 (2016).
Ghimire, S. et al. Generation and propagation of high-order harmonics in crystals. Phys. Rev. A 85, 043836 (2012).
Golde, D., Meier, T. & Koch, S. W. High harmonics generated in semiconductor nanostructures by the coupled dynamics of optical inter- and intraband excitations. Phys. Rev. B 77, 075330 (2008).
Hawkins, P. G., Ivanov, M. Y. & Yakovlev, V. S. Effect of multiple conduction bands on high-harmonic emission from dielectrics. Phys. Rev. A 91, 013405 (2015).
Higuchi, T., Stockman, M. I. & Hommelhoff, P. Strong-field perspective on high-harmonic radiation from bulk solids. Phys. Rev. Lett. 113, 213901 (2014).
Vampa, G., McDonald, C. R., Orlando, G., Corkum, P. B. & Brabec, T. Semiclassical analysis of high harmonic generation in bulk crystals. Phys. Rev. B 91, 064302 (2015).
Vampa, G. et al. Theoretical analysis of high-harmonic generation in solids. Phys. Rev. Lett. 113, 073901 (2014).
Wu, M., Ghimire, S., Reis, D. A., Schafer, K. J. & Gaarde, M. B. High-harmonic generation from Bloch electrons in solids. Phys. Rev. A 91, 043839 (2015).
Kemper, A. F., Moritz, B., Freericks, J. K. & Devereaux, T. P. Theoretical description of high-order harmonic generation in solids. New J. Phys. 15, 023003 (2013).
Al-Naib, I., Sipe, J. E. & Dignam, M. M. High harmonic generation in undoped graphene: interplay of inter- and intraband dynamics. Phys. Rev. B 90, 245423 (2014).
Kelardeh, H. K., Apalkov, V. & Stockman, M. I. Graphene in ultrafast and superstrong laser fields. Phys. Rev. B 91, 045439 (2015).
Kumar, N. et al. Second harmonic microscopy of monolayer MoS2 . Phys. Rev. B 87, 161403 (2013).
Li, Y. et al. Probing symmetry properties of few-layer MoS2 and h-BN by optical second-harmonic generation. Nano Lett. 13, 3329–3333 (2013).
Malard, L. M., Alencar, T. V., Barboza, A. P. M., Mak, K. F. & de Paula, A. M. Observation of intense second harmonic generation from MoS2 atomic crystals. Phys. Rev. B 87, 201401 (2013).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343–350 (2014).
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014).
Chernikov, A. et al. Exciton binding energy and nonhydrogenic Rydberg series in monolayer WS2 . Phys. Rev. Lett. 113, 076802 (2014).
He, K. et al. Tightly bound excitons in monolayer WSe2 . Phys. Rev. Lett. 113, 026803 (2014).
Ye, Z. et al. Probing excitonic dark states in single-layer tungsten disulphide. Nature 513, 214–218 (2014).
Mak, K. F. et al. Tightly bound trions in monolayer MoS2 . Nat. Mater. 12, 207–211 (2013).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2 . Nano Lett. 10, 1271–1275 (2010).
Ellis, J. K., Lucero, M. J. & Scuseria, G. E. The indirect to direct band gap transition in multilayered MoS2 as predicted by screened hybrid density functional theory. Appl. Phys. Lett. 99, 261908 (2011).
Vampa, G. et al. All-optical reconstruction of crystal band structure. Phys. Rev. Lett. 115, 193603 (2015).
Acknowledgements
This project was supported primarily by the Air Force Office of Scientific Research under Grant Nos. FA9550-14-1-0108 and FA9550-14-1-0268. Additional support for Y.L. and T.F.H. was provided by the AMOS program, Chemical Sciences, Geosciences, and Biosciences Division, Basic Energy Sciences, U.S. Department of Energy under Contract No. DE-AC02-76-SFO0515 and by the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant No. GBMF4545. S.G. and Y.S.Y. acknowledge the support from the Office of Science Early Career Research Program. We thank P. H. Bucksbaum for useful discussions.
Author information
Authors and Affiliations
Contributions
H.L. and Y.L. contributed equally to this work, built the experimental set-up, carried out the measurements and analysed the data. D.A.R. and T.F.H. conceived the experiment. H.L., Y.L., Y.S.Y., S.G., T.F.H. and D.A.R. contribute to the interpretation of the data. All authors contributed to the discussions and the preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1563 kb)
Rights and permissions
About this article
Cite this article
Liu, H., Li, Y., You, Y. et al. High-harmonic generation from an atomically thin semiconductor. Nature Phys 13, 262–265 (2017). https://doi.org/10.1038/nphys3946
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3946
This article is cited by
-
Observation of interband Berry phase in laser-driven crystals
Nature (2024)
-
Light-wave-controlled Haldane model in monolayer hexagonal boron nitride
Nature (2024)
-
Topological high-harmonic spectroscopy
Communications Physics (2024)
-
Momentum-dependent intraband high harmonic generation in a photodoped indirect semiconductor
Communications Physics (2024)
-
Light control with Weyl semimetals
eLight (2023)