Abstract
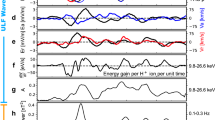
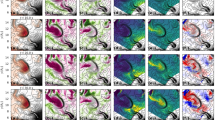
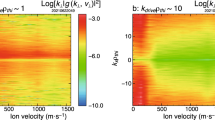
The solar wind is a supersonic magnetized plasma streaming far into the heliosphere. Although cooling as it flows, it is rapidly heated upon encountering planetary obstacles. At Earth, this interaction forms the magnetosphere and its sub-regions. The present paper focuses on particle heating across the boundary separating the shocked solar wind and magnetospheric plasma, which is driven by mechanisms operating on fluid, ion and electron scales. The cross-scale energy transport between these scales is a compelling and fundamental problem of plasma physics. Here, we present evidence of the energy transport between fluid and ion scales: free energy is provided in terms of a velocity shear generating fluid-scale Kelvin–Helmholtz instability. We show the unambiguous observation of an ion-scale magnetosonic wave packet, inside a Kelvin–Helmholtz vortex, with sufficient energy to account for observed ion heating. The present finding has universal consequences in understanding cross-scale energy transport, applicable to environments experiencing velocity shears during comparable plasma regimes.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Borovsky, J. E. & Cayton, T. E. Entropy mapping of the outer electron radiation belt between the magnetotail and geosynchronous orbit. J. Geophys. Res. 116, A06216 (2011).
Hasegawa, H., Fujimoto, M., Maezawa, K., Saito, Y. & Mukai, T. Geotail observations of the dayside outer boundary region: interplanetary magnetic field control and dawn-dusk asymmetry. J. Geophys. Res. 108, 1163 (2003).
Wing, S., Johnson, J. R., Newell, P. T. & Meng, C.-I. Dawn-dusk asymmetries, ion spectra, and sources in the northward interplanetary magnetic field plasma sheet. J. Geophys. Res. 110, A08205 (2005).
Dimmock, A. P., Nykyri, K., Karimabadi, H., Osmane, A. & Pulkkinen, T. I. A statistical study into the spatial distribution and dawn-dusk asymmetry of dayside magnetosheath ion temperatures as a function of upstream solar wind conditions. J. Geophys. Res. 120, 2767–2782 (2015).
Fairfield, D. H. et al. Geotail observations of the Kelvin–Helmholtz instability at the equatorial magnetotail boundary for parallel northward fields. J. Geophys. Res. 105, 21159–21174 (2000).
Hasegawa, H. et al. Transport of solar wind into Earth’s magnetosphere through rolled-up Kelvin–Helmholtz vortices. Nature 430, 755–758 (2004).
Nykyri, K. et al. Cluster observations of reconnection due to the Kelvin–Helmholtz instability at the dawnside magnetospheric flank. Ann. Geophys. 24, 2619–2643 (2006).
Taylor, M. G. G. T. et al. Spatial distribution of rolled up Kelvin–Helmholtz vortices at Earth’s dayside and flank magnetopause. Ann. Geophys. 30, 1025–1035 (2012).
Hwang, K.-J. et al. Kelvin–Helmholtz waves under southward interplanetary magnetic field. J. Geophys. Res. 116, A08210 (2011).
Yan, G. Q. et al. Kelvin–Helmholtz vortices observed by THEMIS at the duskside of the magnetopause under southward interplanetary magnetic field. Geophys. Res. Lett. 41, 4427–4434 (2014).
Kavosi, S. & Raeder, J. Ubiquity of Kelvin–Helmholtz waves at Earth’s magnetopause. Nat. Commun. 6, 7019 (2015).
Pope, S. A. et al. Giant vortices lead to ion escape from Venus and re-distribution of plasma in the ionosphere. Geophys. Res. Lett. 36, L07202 (2009).
Masters, A. et al. Cassini observations of a Kelvin–Helmholtz vortex in Saturn’s outer magnetosphere. J. Geophys. Res. 115, A07225 (2010).
Boardsen, S. A. et al. Observations of Kelvin–Helmholtz waves along the dusk-side boundary of Mercury’s magnetosphere during MESSENGER’s third flyby. Geophys. Res. Lett. 37, L12101 (2010).
Sundberg, T. et al. MESSENGER orbital observations of large-amplitude Kelvin–Helmholtz waves at Mercury’s magnetopause. J. Geophys. Res. 117, A04216 (2012).
Ganguli, G., Slinker, S., Gavrishchaka, V. & Scales, W. Low frequency oscillations in a plasma with spatially variable field-aligned flow. Phys. Plasmas 9, 2321–2329 (2002).
Nykyri, K. et al. Ion cyclotron waves in the high altitude cusp: CLUSTER observations at varying spacecraft separations. Geophys. Res. Lett. 30, 2263 (2003).
Nykyri, K. & Otto, A. Influence of the Hall term on KH instability and reconnection inside KH vortices. Ann. Geophys. 22, 935–949 (2004).
Nakamura, T. K., Hayashi, D., Fujimoto, M. & Shinohara, I. Decay of MHD-scale Kelvin–Helmholtz vortices mediated by parasitic electron dynamics. Phys. Rev. Lett. 92, 145001 (2004).
Nykyri, K. & Otto, A. Plasma transport at the magnetospheric boundary due to reconnection in Kelvin–Helmholtz vortices. Geophys. Res. Lett. 28, 3565–3568 (2001).
Hasegawa, H. et al. Kelvin–Helmholtz waves at the Earth’s magnetopause: multiscale development and associated reconnection. J. Geophys. Res. 114, A12207 (2009).
Rossi, C. et al. Two-fluid numerical simulations of turbulence inside Kelvin–Helmholtz vortices: intermittency and reconnecting current sheets. Phys. Plasmas 22, 122303 (2015).
Palermo, F., Faganello, M., Califano, F. & Pegoraro, F. Kelvin–Helmholtz vortices and secondary instabilities in super-magnetosonic regimes. Ann. Geophys. 29, 1169–1178 (2011).
Zieger, B. et al. Jet front-driven mirror modes and shocklets in the near-Earth flow-braking region. Geophys. Res. Lett. 38, L22103 (2011).
Hasegawa, H. et al. Single-spacecraft detection of rolled-up Kelvin–Helmholtz vortices at the flank magnetopause. J. Geophys. Res. 111, A09203 (2006).
Stasiewicz, K. et al. Small scale Alfvénic structure in the Aurora. Space Sci. Rev. 92, 423–533 (2000).
Stix, T. H. Waves in Plasmas (American Institute of Physics, 1992).
Krauss-Varban, D., Omidi, N. & Quest, K. B. Mode properties of low-frequency waves: kinetic theory versus Hall-MHD. J. Geophys. Res. 99, 5987–6009 (1994).
Roennmark, K. Waves in homogeneous, anisotropic multicomponent plasmas (WHAMP) Tech. Rep. (Kiruna Geophysical Institute, 1982).
Colpitts, C. A., Cattell, C. A., Kozyra, J. U. & Parrot, M. Satellite observations of banded vlf emissions in conjunction with energy-banded ions during very large geomagnetic storms. J. Geophys. Res. 117, A10211 (2012).
Perraut, S. et al. A systematic study of ULF waves above F/H plus/ from GEOS 1 and 2 measurements and their relationships with proton ring distributions. J. Geophys. Res. 87, 6219–6236 (1982).
Boardsen, S. A., Gallagher, D. L., Gurnett, D. A., Peterson, W. K. & Green, J. L. Funnel-shaped, low-frequency equatorial waves. J. Geophys. Res. 97, 14967–14976 (1992).
Meredith, N. P., Horne, R. B. & Anderson, R. R. Survey of magnetosonic waves and proton ring distributions in the Earth’s inner magnetosphere. J. Geophys. Res. 113, A06213 (2008).
Balikhin, M. A. et al. Observations of discrete harmonics emerging from equatorial noise. Nat. Commun. 6, 7703 (2015).
Walker, S. N. et al. Experimental determination of the dispersion relation of magnetosonic waves. J. Geophys. Res. 9632–9650 (2015).
Min, K. & Liu, K. Fast magnetosonic waves driven by shell velocity distributions. J. Geophys. Res. 120, 2739–2753 (2015).
Terasawa, T. & Nambu, M. Ion heating and acceleration by magnetosonic waves via cyclotron subharmonic resonance. Geophys. Res. Lett. 16, 357–360 (1989).
Peñano, J. R. & Ganguli, G. Ionospheric source for low-frequency broadband electromagnetic signatures. Phys. Rev. Lett. 83, 1343–1346 (1999).
Peñano, J. R. & Ganguli, G. Generation of ELF electromagnetic waves in the ionosphere by localized transverse dc electric fields: subcyclotron frequency regime. J. Geophys. Res. 105, 7441–7458 (2000).
Peñano, J. R. & Ganguli, G. Correction to “Generation of ELF electromagnetic waves in the ionosphere by localized transverse dc electric fields: subcyclotron frequency regime” by J. R. Peñano and G. Ganguli. J. Geophys. Res. 107, SIA 7-1–SIA 7-2 (2002).
Tejero, E. M. et al. Spontaneous electromagnetic emission from a strongly localized plasma flow. Phys. Rev. Lett. 106, 185001 (2011).
Ganguli, G., Tejero, E., Crabtree, C., Amatucci, W. & Rudakov, L. Generation of electromagnetic waves in the very low frequency band by velocity gradient. Phys. Plasmas 21, 012107 (2014).
Hunana, P. et al. Polarization and compressibility of oblique kinetic Alfvén waves. Astrophys. J. 766, 93 (2013).
Johnson, J. R., Cheng, C. Z. & Song, P. Signatures of mode conversion and kinetic Alfvén waves at the magnetopause. Geophys. Res. Lett. 28, 227–230 (2001).
Chaston, C. C. et al. Mode conversion and anomalous transport in Kelvin–Helmholtz vortices and kinetic Alfvén waves at the Earth’s magnetopause. Phys. Rev. Lett. 99, 175004 (2007).
Johnson, J. R. & Cheng, C. Z. Stochastic ion heating at the magnetopause due to kinetic Alfvén waves. Geophys. Res. Lett. 28, 4421–4424 (2001).
Nykyri, K. Impact of MHD shock physics on magnetosheath asymmetry and Kelvin–Helmholtz instability. J. Geophys. Res. 118, 5068–5081 (2013).
Nykyri, K. & Dimmock, A. Statistical study of the {ULF} pc4 pc5 range fluctuations in the vicinity of earths magnetopause and correlation with the low latitude boundary layer thickness. Adv. Space Res. 257–267 (2016).
Yao, Y., Chaston, C. C., Glassmeier, K.-H. & Angelopoulos, V. Electromagnetic waves on ion gyro-radii scales across the magnetopause. Geophys. Res. Lett. 38, L09102 (2011).
Foullon, C., Verwichte, E., Nakariakov, V. M., Nykyri, K. & Farrugia, C. J. Magnetic Kelvin–Helmholtz Instability at the Sun. Astrophys. J. Lett. 729, L8 (2011).
Horton, W., Perez, J. C., Carter, T. & Bengtson, R. Vorticity probes and the characterization of vortices in the Kelvin–Helmholtz instability in the large plasma device experiment. Phys. Plasmas 12, 022303 (2005).
Ongena, J., Koch, R., Wolf, R. & Zohm, H. Magnetic-confinement fusion. Nat. Phys. 12, 398–410 (2016).
Paschmann, G. & Daly, P. W. Analysis Methods for Multi-Spacecraft Data ISSI Scientific Reports Series SR-001, ESA/ISSI, Vol. 1. ISBN 1608-280X, 1998 1 (ISSI Scientific Reports Series, ESA Publications Division, 1998).
Otto, A. & Fairfield, D. H. Kelvin–Helmholtz instability at the magnetotail boundary: MHD simulation and comparison with Geotail observations. J. Geophys. Res. 105, 21175–21190 (2000).
Balikhin, M. A. et al. Experimental determination of the dispersion of waves observed upstream of a quasi-perpendicular shock. Geophys. Res. Lett. 24, 787–790 (1997).
Dimmock, A. P., Balikhin, M. A., Walker, S. N. & Pope, S. A. Dispersion of low frequency plasma waves upstream of the quasi-perpendicular terrestrial bow shock. Ann. Geophys. 31, 1387–1395 (2013).
Sonnerup, B. U. O. & Cahill, L. J. Jr Magnetopause structure and attitude from explorer 12 observations. J. Geophys. Res. 72, 171–173 (1967).
Laakso, H. et al. Cluster active archive: overview. Astrophys. Space Sci. Proc. 11, 3–37 (2010).
Acknowledgements
The work of T.W.M. and K.N. was supported by National Science Foundation Grants 0847120 and 1502774. The work of A.P.D. was supported by the Academy of Finland Grants 288472 and 267073/2013. The authors would like to thank M. A. Balikhin for valuable discussion. The authors would like to acknowledge the work performed by the Cluster FGM, EFW, CIS and PEACE instrument teams as well as the Cluster Science Archive and the Cluster Active Archive for the use of their data.
Author information
Authors and Affiliations
Contributions
K.N. provided the idea, initiated the study and guided the work of graduate student T.W.M., who identified the KH event from Cluster data, screened the data for plasma mixing regions and higher frequency plasma waves, analysed wave properties, created 2.5D MHD simulations of the event and prepared figures for the manuscript. A.P.D. computed the experimental dispersion relation using the two-spacecraft method. All authors contributed to the writing and editing of the manuscript and discussed the methods, results and scientific implications at all stages. All authors discussed the text and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1552 kb)
Rights and permissions
About this article
Cite this article
Moore, T., Nykyri, K. & Dimmock, A. Cross-scale energy transport in space plasmas. Nature Phys 12, 1164–1169 (2016). https://doi.org/10.1038/nphys3869
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3869
This article is cited by
-
Review of Mercury’s dynamic magnetosphere: Post-MESSENGER era and comparative magnetospheres
Science China Earth Sciences (2022)
-
Particle energization in space plasmas: towards a multi-point, multi-scale plasma observatory
Experimental Astronomy (2022)
-
Observing Kelvin–Helmholtz instability in solar blowout jet
Scientific Reports (2018)
-
Kelvin–Helmholtz Instability: Lessons Learned and Ways Forward
Space Science Reviews (2018)
-
A journey through scales
Nature Physics (2016)