Abstract
Numerical simulations are a versatile tool for providing insight into the complicated process of structure formation in cosmology1. This process is mainly governed by gravity, which is the dominant force on large scales. At present, a century after the formulation of general relativity2, numerical codes for structure formation still employ Newton’s law of gravitation. This approximation relies on the two assumptions that gravitational fields are weak and that they originate from non-relativistic matter. Whereas the former seems well justified on cosmological scales, the latter imposes restrictions on the nature of the ‘dark’ components of the Universe (dark matter and dark energy), which are, however, poorly understood. Here we present the first simulations of cosmic structure formation using equations consistently derived from general relativity. We study in detail the small relativistic effects for a standard lambda cold dark matter cosmology that cannot be obtained within a purely Newtonian framework. Our particle-mesh N-body code computes all six degrees of freedom of the metric and consistently solves the geodesic equation for particles, taking into account the relativistic potentials and the frame-dragging force. This conceptually clean approach is very general and can be applied to various settings where the Newtonian approximation fails or becomes inaccurate, ranging from simulations of models with dynamical dark energy3 or warm/hot dark matter4 to core collapse supernova explosions5.
Similar content being viewed by others
Main
The applicability of Newton’s law of gravitation in the context of cosmic structure formation has been discussed extensively in the recent literature6,7,8. In particular, it is now well understood that this simplified description is fairly accurate when applied within standard lambda cold dark matter (ΛCDM) cosmology where perturbations come entirely from non-relativistic matter. However, the situation is not satisfactory for two reasons. First, the quality of observational data is rapidly increasing, and upcoming galaxy surveys will eventually reach a precision where a naive treatment of the effects of spacetime geometry becomes insufficient9,10. Second, the true nature of dark matter and dark energy is not yet established. To study models beyond ΛCDM, some of which may feature relativistic sources of stress-energy, employing the Newtonian approximation is not always justified. A number of numerical codes have been developed for particular models11,12,13,14, yet a general framework would be desirable. Furthermore, Newtonian gravity is acausal and not sensitive to the presence of a cosmological horizon. Even if a judicious interpretation of the output of Newtonian simulations can cure this problem at the linear level, it comes back when one goes beyond linear perturbation theory, and it would be preferable to use the correct physics from the outset.
Moving from the absolute space and time of the Newtonian picture towards a general relativistic view where geometry is dynamical poses a significant conceptual challenge. Recent progress is owed to a suitable formulation of the relativistic setting in terms of a weak-field expansion which is well adapted for (but not restricted to) cosmological applications7,15,16. Based on these ideas we have developed a numerical code, gevolution, which uses the LATfield2 library17 and is designed to perform cosmological N-body simulations fully in the context of general relativity, evolving all six metric degrees of freedom. In brief, our approach can be summarized as follows.
We choose a suitable ansatz for the metric which is split into background and perturbations. We work in Poisson gauge where the perturbed Friedmann–Lemaître–Robertson–Walker metric is

where a denotes the scale factor of the background, xi are comoving coordinates on the spacelike hypersurfaces, and τ is conformal time. ϕ and Ψ are the Bardeen potentials that describe the scalar metric perturbations; Bi (also denoted as B) is transverse and is responsible for frame dragging; hij is transverse and traceless, it contains the two spin-2 degrees of freedom of gravitational waves.
We also assume that the perturbations of the metric, but not necessarily their derivatives, remain small on the scales of interest. This is a valid approximation for cosmological scales even when perturbations in the stress-energy tensor are large.
Einstein’s equations are then expanded in terms of the metric perturbations, but without a perturbative treatment of the stress-energy tensor. We include all terms linear in metric perturbations and go to quadratic order in terms which have two spatial derivatives acting on ϕ, Ψ. This weak-field expansion contains all six components of the metric correctly at leading order. To determine the evolution of the metric, we numerically solve the ‘00’ and the traceless part of the ‘ij’ Einstein equations:


Equation (2) is the generalization of the Newtonian Poisson equation (Δϕ = 4πGa2δρ) and contains additional relativistic terms. Here Δϕ and  are not required to be small—in fact, they become much larger than the background value
are not required to be small—in fact, they become much larger than the background value  inside dense regions. Equation (3) can be used to evolve all the non-Newtonian degrees of freedom of the metric: ϕ − Ψ, the two spin-1 degrees of freedom, B, and the two spin-2 helicities, hij. To do this, we decompose the equation into scalar, vector and tensor parts in Fourier space.
inside dense regions. Equation (3) can be used to evolve all the non-Newtonian degrees of freedom of the metric: ϕ − Ψ, the two spin-1 degrees of freedom, B, and the two spin-2 helicities, hij. To do this, we decompose the equation into scalar, vector and tensor parts in Fourier space.
The metric is then used to solve the equations of motion for matter (and possibly other degrees of freedom); collisionless particles propagate along geodesics in the perturbed geometry. This determines the evolution of the stress-energy tensor.
As a first application we choose standard ΛCDM cosmology. We expect only small effects in this case, but we can use these simulations to gain confidence in our new approach. We generate18 two halo catalogues containing ∼500,000 halos each, one using our relativistic approach and one with the traditional Newtonian approach as reference, starting from identical linear initial conditions. A Kolmogorov–Smirnov test shows no significant disagreement in the distributions of some 25 different halo properties such as mass, spin or shape parameters.
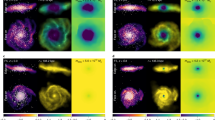
The largest non-Newtonian effect is frame dragging, which is associated with the spin-1 perturbation B. This perturbation is sourced by the curl part of the momentum density found, for example, in rotating massive objects. As long as perturbations are small this is a second-order effect which has been studied using perturbation theory19. The power spectrum for B has also been computed in the non-perturbative regime of structure formation using a post-Newtonian framework20 which is expected to give good agreement with our approach as long as one considers ΛCDM (ref. 16). These results are useful benchmarks for our code, but we now go beyond: our simulations track the full three-dimensional realization of B (see Fig. 1). We can therefore measure the actual frame-dragging force on individual particles.
Visualization of a simulation volume of (512 Mpc/h)3 at redshift z = 0. Dark matter halos are rendered as orange blobs scaled to the virial radius. a, Illustration of the spin-2 perturbation hij by applying it as affine transformation to spheroids of fixed radius; the shape and size of the resulting ellipsoids therefore indicates, respectively, the polarization and amplitude of the tensor perturbation. Note how the signal is dominated by long-wavelength perturbations that are significantly correlated with the matter distribution. b, Stream plot of the spin-1 perturbation B, indicating how ‘spacetime is dragged around’ by vortical matter flows. (The Supplementary Material contains movies that also show the time evolution of the simulation.)
Whereas the typical gravitational acceleration on Mpc scales is of the order of 10−9 cm s−2, frame dragging contributes only at the level of 10−14 cm s−2 (both numbers are mass-weighted r.m.s. values from our simulations at redshift zero), and the highest value we measure is some 10−12 cm s−2. Thus, for objects moving at 1,000 km s−1 (a typical peculiar velocity at those scales) the Δv due to frame dragging is no more than 1 km s−1. It should be noted that these numbers are scale dependent, as the acceleration is larger on smaller scales.
We compare our simulation results also with predictions21,22 from second-order perturbation theory for the power spectra of hij, of B and of ϕ − Ψ. The latter requires regularization in the infrared, which is implemented by the finite volume of the simulation.
To fully capture the amplitude of the non-Newtonian terms, it is important that the scale of matter–radiation equality is represented in the simulation volume. On the other hand, these terms are generated by nonlinearities and are therefore amplified at small scales. To obtain our results we had to cover at least three orders of magnitude in scale. Our largest simulation used a lattice with 4,0963 points, corresponding to 6.7 × 1010 particles as we always start with one particle per grid point. This simulation used 16384 CPUs on the Cray XC30 supercomputer Piz Daint; its 1088 time steps were completed in about 7 h, therefore totalling about 115 000 CPU hours.
Figure 2 shows the numerical power spectra at three redshifts. For these spectra we used eight simulations with lattices of 2,0483 points and two different box sizes, all starting at redshift z = 100. Four simulations had a box size of (2,048 Mpc/h)3, the other four were (512 Mpc/h)3. In the regime where it can be trusted we find excellent agreement with second-order perturbation theory, which demonstrates that our code produces valid results. At late times and on small scales, perturbation theory breaks down. Nonlinearities enhance the frame dragging by more than an order of magnitude at redshifts z = 1 and z = 0 and on scales k ≳ 1h/Mpc. In this regime its power spectrum is only a factor 10−4 times smaller than the one of the Newtonian potential. This means that frame dragging is potentially an order 1% effect. Tensor perturbations on the other hand, even though they are enhanced by more than three orders of magnitude, remain a feeble contribution. Of course these power spectra are not directly observable: when comparing calculations with observations a projection onto the light cone has to be performed. This has been studied within perturbation theory23, and one could implement this procedure also in our N-body code, for example, by ray-tracing photons through the simulation box.
Power spectra of the gravitational potential ϕ (top, violet), the frame-dragging potential B (second from top, blue), the difference between the relativistic potentials ϕ − Ψ (third from top, red) and the tensor perturbation hij (bottom, green) at redshifts z = 10, 1, 0. The black lines (dashed, dot-dashed, dot-dot-dashed, and dotted) indicate the corresponding results from second-order perturbation theory. As expected, the numerical results deviate from these perturbative extrapolations at low redshift and small scales. All perturbation variables are significantly enhanced on scales k ≳ 1h/Mpc at redshift z = 1 and below. Error bars indicate the random fluctuations from different realizations.
It should finally be noted that our framework jointly solves for background and perturbations in a self-consistent way. Therefore, we confirm that clustering has only a small effect on the expansion rate of the Universe. The non-Newtonian effects which we have quantified in the nonlinear regime of structure formation remain small within a ΛCDM Universe, but they may nevertheless be measurable in the future. The vorticity, which is related to frame dragging, is substantial on small scales and remains at the per cent level relative to the gradient velocity field even on large scales. This can lead to observable corrections in redshift–space distortions. A detailed analysis of this possibility is still missing.
For the first time, general relativity has been implemented as the theory of gravity in a cosmological N-body code, making it possible to feed these effects back into the dynamics. Our numerical framework will be particularly useful in scenarios where relativistic sources are present, such as models of dynamical dark energy, topological defects, or with relativistic particles such as neutrinos or warm dark matter. Such scenarios are expected to exhibit larger relativistic effects. Contrary to Newtonian schemes, we are also able to solve the full geodesic equation for arbitrary velocities, allowing for a realistic propagation of radiation or high-velocity particles.
Methods
A weak-field expansion is useful in situations where the metric perturbation variables ϕ, Ψ, Bi, hij defined in equation (1) are small, as is the case on cosmological scales. To get a tractable set of equations, we retain all terms which are linear in metric perturbations, but of the quadratic terms we keep only the most relevant ones. These are built from the scalar perturbations ϕ and Ψ only, and contain the highest possible number of spatial derivatives (two in this case, as all the partial differential equations are second order). This is enough to ensure that all six metric degrees of freedom are treated correctly at leading order, even in cases where some of them are strongly suppressed.
The implementation in gevolution adopts a particle-mesh scheme where the metric field is represented on a regular cubic lattice whereas matter takes the form of an N-body ensemble of particles that samples the six-dimensional phase space. The stress-energy tensor on the lattice is obtained by a particle-to-mesh projection and is used in Einstein’s equations to solve for the metric perturbations. Finally, the particles are evolved by interpolating the metric to the particle positions and integrating the geodesic equation. gevolution is built on top of the LATfield2 C++ framework17. LATfield2 distributes the fields and the particles over a two-dimensional process grid (using MPI). It also provides the Fast Fourier Transform which gevolution needs for solving equations (2) and (3).
Einstein’s equations.
We determine the metric perturbations using the time–time as well as the traceless space–space part of Einstein’s equations given in equations (2) and (3). The remaining four equations are redundant, but we can use them as consistency check. The stress-energy tensor is constructed in the perturbed geometry and may hence also contain some terms which are linear in the metric perturbations—these terms have to be taken into account to maintain consistency. For a ΛCDM cosmology, such as the one studied here, the stress-energy tensor is obtained numerically by appropriate particle-to-mesh projections which are ‘dressed’ by these geometric corrections.
We then solve for the metric variables by treating the quadratic terms in equations (2) and (3) as small perturbations. To this end, we simply estimate their value using the solutions taken from the previous time step and move them to the right-hand side. As the equations are then approximated as linear in the metric perturbations, we use Fourier methods16 to obtain the new solutions. This is convenient in particular as the gauge conditions can easily be implemented in Fourier space, where they reduce to local projection operations. One can check that the new solutions are stable by reinserting them into the quadratic terms and iterating the procedure.
Particle trajectories.
As dark matter is assumed to be collisionless, the particles move along geodesics. For non-relativistic velocities v = dx/dτ, the geodesic equation reads

where the B-dependent terms account for frame dragging. The integration of this equation can be simplified by writing  , which transforms equation (4) to
, which transforms equation (4) to

This new equation actually describes the acceleration as seen in a Gaussian orthonormal coordinate frame. Frame dragging, characterized by the last term, has to compete with the ‘Newtonian’ force ∇Ψ. We measure both forces individually in our simulations.
Supplementary Fig. 1 shows the mass-weighted r.m.s. value of the frame dragging acceleration  for simulations with different spatial resolutions. The simulation volume was (512 Mpc/h)3 in all cases, but we used lattice sizes from 5123 to 40963 points, reaching a best resolution of 125 kpc/h. The r.m.s. acceleration depends on the scale probed and therefore also on resolution—the frame-dragging acceleration is larger on smaller scales, but the main contribution comes from large scales. Supplementary Fig. 2 shows a more detailed stream plot of the spin-1 perturbation, revealing its long-range correlation and its correlation with the distribution of matter. At our best resolution we remain slightly above galactic scales. At smaller scales we expect baryonic effects to become important.
for simulations with different spatial resolutions. The simulation volume was (512 Mpc/h)3 in all cases, but we used lattice sizes from 5123 to 40963 points, reaching a best resolution of 125 kpc/h. The r.m.s. acceleration depends on the scale probed and therefore also on resolution—the frame-dragging acceleration is larger on smaller scales, but the main contribution comes from large scales. Supplementary Fig. 2 shows a more detailed stream plot of the spin-1 perturbation, revealing its long-range correlation and its correlation with the distribution of matter. At our best resolution we remain slightly above galactic scales. At smaller scales we expect baryonic effects to become important.
Power spectra.
In Fig. 2 we show the power spectra of the metric perturbations which are defined by



Here Pij = δij − kikj/k2 is the transverse projector and the spin-2 projection operator is given by Mijlm = PilPjm + PimPjl − PijPlm. These dimensionless power spectra measure the amplitude square of the metric perturbations at scale k per logk interval. To suppress finite-volume and resolution effects we measure only scales which are at least five times smaller than the box size and have a wavenumber which is at least five times smaller than the Nyquist frequency.
The second-order power spectra of ϕ − Ψ and of B decay as ∼k−3.7 on small scales, whereas the tensor spectrum decays as ∼k−7.3. Nonlinear evolution considerably flattens all the spectra around k ∼ 1h/ Mpc to slopes between −2 and −3.
Initial conditions.
Initial data is generated using a linear input power spectrum at initial redshift (we start at z = 100) which can be obtained by running a Boltzmann code24,25 for the model. We use CLASS with the default cosmological parameters which describe a ΛCDM model (Ωm = Ωc + Ωb = 0.312, our code at present has no special treatment for baryonic matter). The initial displacement of the particles is also computed at linear order, taking into account our choice of gauge15.
Code availability.
The gevolution code is available on a public Git repository: https://github.com/gevolution-code/gevolution-1.0.git. The required extension of the LATfield2 library is developed independently and is available on the repository: https://github.com/daverio/LATfield2.git.
References
Springel, V. et al. Simulating the joint evolution of quasars, galaxies and their large-scale distribution. Nature 435, 629–636 (2005).
Einstein, A. The field equations of gravitation. Sitz.ber. Preuss. Akad. Wiss. Berlin 1915, 844–847 (1915).
Noller, J., von Braun-Bates, F. & Ferreira, P. G. Relativistic scalar fields and the quasistatic approximation in theories of modified gravity. Phys. Rev. D 89, 023521 (2014).
Costanzi, M. et al. Cosmology with massive neutrinos III: the halo mass function and an application to galaxy clusters. JCAP 1312, 012 (2013).
Kotake, K. Multiple physical elements to determine the gravitational-wave signatures of core-collapse supernovae. C. R. Phys. 14, 318–351 (2013).
Chisari, N. E. & Zaldarriaga, M. Connection between Newtonian simulations and general relativity. Phys. Rev. D 83, 123505 (2011).
Green, S. R. & Wald, R. M. Newtonian and relativistic cosmologies. Phys. Rev. D 85, 063512 (2012).
Rigopoulos, G. & Valkenburg, W. On the accuracy of N-body simulations at very large scales. Mon. Not. R. Astron. Soc. 446, 677–682 (2015).
Yoo, J. & Zaldarriaga, M. Beyond the linear-order relativistic effect in galaxy clustering: second-order gauge-invariant formalism. Phys. Rev. D 90, 023513 (2014).
Bonvin, C. Isolating relativistic effects in large-scale structure. Class. Quantum Gravity 31, 234002 (2014).
Schmidt, F. Self-consistent cosmological simulations of DGP braneworld gravity. Phys. Rev. D 80, 043001 (2009).
Li, B., Zhao, G.-B., Teyssier, R. & Koyama, K. ECOSMOG: an efficient COde for simulating modified gravity. JCAP 1201, 051 (2012).
Puchwein, E., Baldi, M. & Springel, V. Modified-Gravity-GADGET: a new code for cosmological hydrodynamical simulations of modified gravity models. Mon. Not. R. Astron. Soc. 436, 348–360 (2013).
Llinares, C., Mota, D. F. & Winther, H. A. ISIS: a new N-body cosmological code with scalar fields based on RAMSES. Code presentation and application to the shapes of clusters. Astron. Astrophys. 562, A78 (2014).
Adamek, J., Daverio, D., Durrer, R. & Kunz, M. General relativistic N-body simulations in the weak field limit. Phys. Rev. D 88, 103527 (2013).
Adamek, J., Durrer, R. & Kunz, M. N-body methods for relativistic cosmology. Class. Quantum Gravity 31, 234006 (2014).
Daverio, D., Hindmarsh, M. & Bevis, N. Latfield2: a C++ library for classical lattice field theory. Preprint at http://arXiv.org/abs/1508.05610 (2015).
Behroozi, P. S., Wechsler, R. H. & Wu, H.-Y. The Rockstar phase-space temporal halo finder and the velocity offsets of cluster cores. Astrophys. J. 762, 109 (2013).
Lu, T. H.-C., Ananda, K., Clarkson, C. & Maartens, R. The cosmological background of vector modes. JCAP 0902, 023 (2009).
Bruni, M., Thomas, D. B. & Wands, D. Computing general relativistic effects from Newtonian N-body simulations: frame dragging in the post-Friedmann approach. Phys. Rev. D 89, 044010 (2014).
Ananda, K. N., Clarkson, C. & Wands, D. Cosmological gravitational wave background from primordial density perturbations. Phys. Rev. D 75, 123518 (2007).
Baumann, D., Steinhardt, P. J., Takahashi, K. & Ichiki, K. Gravitational wave spectrum induced by primordial scalar perturbations. Phys. Rev. D 76, 084019 (2007).
Bonvin, C. & Durrer, R. What galaxy surveys really measure. Phys. Rev. D 84, 063505 (2011).
Lewis, A., Challinor, A. & Lasenby, A. Efficient computation of cosmic microwave background anisotropies in closed Friedmann–Robertson–Walker models. Astrophys. J. 538, 473–476 (2000).
Blas, D., Lesgourgues, J. & Tram, T. The Cosmic Linear Anisotropy Solving System (CLASS). Part II: approximation schemes. JCAP 1107, 034 (2011).
Acknowledgements
We thank R. Teyssier and M. Bruni for discussions. This work was supported by the Swiss National Supercomputing Centre (CSCS) under project ID s546. The numerical simulations were carried out on Piz Daint at the CSCS and on the Baobab cluster of the University of Geneva. Financial support was provided by the Swiss National Science Foundation.
Author information
Authors and Affiliations
Contributions
J.A. worked out the equations in our approximation scheme and implemented the cosmological code gevolution. He also produced the figures. D.D. developed and implemented the particle handler for the LATfield2 framework. R.D. contributed to the development of the approximation scheme and the derivation of the equations. M.K. proposed the original idea. All authors discussed the research and helped with writing the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 886 kb)
Supplementary Movie 1
Supplementary Movie (MPG 10504 kb)
Supplementary Movie 2
Supplementary Movie (MPG 7958 kb)
Rights and permissions
About this article
Cite this article
Adamek, J., Daverio, D., Durrer, R. et al. General relativity and cosmic structure formation. Nature Phys 12, 346–349 (2016). https://doi.org/10.1038/nphys3673
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3673
This article is cited by
-
The averaging problem on the past null cone in inhomogeneous dust cosmologies
General Relativity and Gravitation (2023)
-
Testing general relativity with cosmological large scale structure
General Relativity and Gravitation (2022)
-
Beyond Schrödinger-Poisson: nonrelativistic effective field theory for scalar dark matter
Journal of High Energy Physics (2021)
-
The detection of relativistic corrections in cosmological N-body simulations
Celestial Mechanics and Dynamical Astronomy (2020)
-
Mathematical general relativity
General Relativity and Gravitation (2019)