Abstract
Nematic fluctuations and order play a prominent role in material classes such as the cuprates1, some ruthenates2 or the iron-based compounds3,4,5,6 and may be interrelated with superconductivity7,8,9,10,11. In iron-based compounds12 signatures of nematicity have been observed in a variety of experiments. However, the fundamental question as to the relevance of the related spin13, charge9,14 or orbital8,15,16 fluctuations remains open. Here, we use inelastic light (Raman) scattering and study Ba(Fe1−xCox)2As2 (0 ≤ x ≤ 0.085) for getting direct access to nematicity and the underlying critical fluctuations with finite characteristic wavelengths17,18,19,20,21. We show that the response from fluctuations appears only in B1g (x2 − y2) symmetry (1 Fe unit cell). The scattering amplitude increases towards the structural transition at Ts but vanishes only below the magnetic ordering transition at TSDW < Ts, suggesting a magnetic origin of the fluctuations. The theoretical analysis explains the selection rules and the temperature dependence of the fluctuation response. These results make magnetism the favourite candidate for driving the series of transitions.
Similar content being viewed by others
Main
The magneto-structural phase transition is among the most thoroughly studied phenomena in iron-based materials. When Fe is substituted by Co in BaFe2As2 the structural transformation at Ts precedes the magnetic ordering at TSDW < Ts (ref. 22). The nematic phase between Ts and TSDW is characterized by broken C4 symmetry but preserved O(3) spin rotational symmetry (no magnetic order). Nematic fluctuations are present even above Ts in the tetragonal phase, as has been demonstrated by both elastoresistance measurements4,6 and studies of the elastic constants23,24. In strained samples, one observes orbital ordering in the photoemission spectra25 and electronic nematicity by transport4,26. However, it is rather difficult to derive the dynamics and critical momentum typical for the underlying fluctuations and to identify which of the ordering phenomena drives the instabilities.
Raman scattering provides experimental access to all types of dynamic nematicity although only the charge sector has been studied in more detail9,14,27,28. However, also in the case of spin-driven nematic order the technique can play a prominent role for coupling to a two-spin operator whereas a four-spin correlation function is the lowest order contribution to the neutron cross-section5. We exploit this advantage here and study the low-energy Raman response of Ba(Fe1−xCox)2As2 experimentally and interpret the results in terms of a microscopic model for a spin-driven nematic phase. In addition to earlier work9,14,20 we study the temperature dependence of the response in the crucial range between Ts and TSDW in great detail and address the spectral shape and the selection rules enabling us to explain the structural and magnetic transitions in a unified microscopic picture.
We study Ba(Fe1−xCox)2As2 single crystals, having x = 0, x = 0.025 and x = 0.051 (see Methods), as a function of photon polarization in the temperature range 4.2 < T ≤ 300 K. For the symmetry assignment we use the 1 Fe unit cell in which the fluctuations appear in B1g symmetry. We use the appearance of twin boundaries and of the As A1g (x2 + y2) phonon line as internal thermometers for the structural and the magnetic phase transitions, respectively. In this way, Ts and TSDW can be determined with a precision of typically ±0.2 and ±1 K, respectively.
Figure 1 shows the Raman response Rχ′′(Ω, T) for Ba(Fe0.975Co0.025)2As2 for various temperatures in A1g and B1g (1 Fe per unit cell) symmetry. B2g spectra were measured only at a few temperatures and found to be nearly temperature independent in agreement with previous data14. Results for other doping levels x are shown in Supplementary Figs 2 and 3. The spectra comprise a superposition of several types of excitation including narrow phonon lines and slowly varying continua arising from electron–hole (e–h) pairs; hence, the continuum reflects the dynamical two-particle behaviour. The A1g and B1g spectra predominantly weigh out contributions from the central hole bands and the electron bands, respectively29. The symmetry-dependent initial slope τ0, μ(T) (μ = A1g, B1g, B2g) (see Fig. 1a, c) can be compared to transport data. [τ0, μ(T)]−1 corresponds to the static transport relaxation rate Γ0, μ(T) of the conduction electrons. The memory function method facilitates the quantitative determination of the dynamic relaxation Γ(Ω, T) in absolute energy units. The static limit can be obtained by extrapolation, Γ0, μ(T) = Γμ(Ω → 0, T) (see Methods and Supplementary Information III). In Fig. 1d we show the result for x = 0.025 corresponding to the spectra of Fig. 1a–c. The results for all doping levels studied are compiled in Supplementary Fig. 4 and compared to the scattering rates derived from the resistivities22.
a–c, Raman response Rχ′′(Ω, T) (raw data after division by the Bose–Einstein factor) in B1g above (a) and below (b) Ts, and A1g symmetry (c) at temperatures as indicated. The initial slopes shown in a and c as grey arrows are proportional to the static two-particle lifetime in symmetry μ = A1g, B1g. d, Raman relaxation rates Γ0, μ(T) in A1g (blue circles) and B1g (red diamonds) symmetry as a function of temperature (see Methods). The fluctuation range Ts < T < Tf and the nematic phase TSDW < T < Ts are indicated in green and magenta, respectively.
Figure 1d shows one of the central results: above approximately 200 K Γ0, μ(T) varies slowly and similarly in both symmetries. The more rapid decrease of Γ0, B1g(T) below 200 K is accompanied by a strong intensity gain in the range 20–200 cm−1 (see Fig. 1a) as observed before in similar samples9,14,28. The intensity gain indicates that there is an additional contribution superposed on the e–h continuum that, as will be shown below, arises from fluctuations. Therefore, the kink in Γ0, B1g(T) is labelled Tf and marks the crossover temperature below which nematic fluctuations can be observed by Raman scattering. At least for low doping, Tf is relatively well defined. The kink allows us to separate the two regimes of the low-energy response above and below Tf as being dominated by carrier excitations and fluctuations, respectively.
The additional B1g signal below Tf has to be treated in a way different from that in A1g symmetry and in B1g above Tf. As it is rather strong it can be separated out with little uncertainty by subtracting the e–h continuum. We approximate the continuum at Tf by an analytic function that is then determined for each temperature according to the variation of the resistivity and the A1g spectra and subtracted from all spectra at lower temperatures. The details are explained in Supplementary Information VII. The results of the subtraction procedure are shown in Fig. 2. The response increases rapidly towards Ts without however diverging, and the maximum moves to lower energies.
a,b, Results above Ts = 102.8 K (a) and between Ts and TSDW = 98 K (b). The red lines are theoretical predictions on the basis of Aslamazov–Larkin diagrams17 describing the exchange of a pair of fluctuations (for details see Supplementary Information IV and V).
As a surprise, the fluctuations do not disappear directly below Ts (Fig. 2b) as one would expect if long-ranged order would be established. Rather, the intensity decreases continuously and the maximum stays approximately pinned implying that the correlation length does not change substantially between the two transitions at Ts = 102.8 ± 0.2 K and TSDW = 98 ± 1 K. The persistence of the fluctuations down to TSDW strongly favours their magnetic origin.
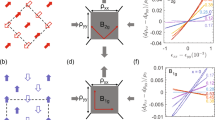
We first compare the data to the theoretical model for thermally driven spin fluctuations associated with the striped magnetic phase ordering along Qx = (π, 0) or Qy = (0, π). In leading order two non-interacting fluctuations carrying momenta Q and −Q are exchanged. Electronic loops (see Fig. 3 and Supplementary Fig. 5) connect the photons and the fluctuations and entail Q-dependent selection rules, which were derived along with the spectral response R0, μ(Ω) in ref. 17 and are summarized in Supplementary Information IV. In brief, because the response results from a sum over all electronic momenta close to the Fermi surface cancellation effects may occur if Q connects parts on different Fermi surface sheets having form factors γμ(k) with opposite sign. For the ordering vectors (π, 0) and (0, π) the resulting selection rules explain the enhancement of the signal in B1g symmetry and its absence in the A1g and B2g channels.
The paramagnetic coupling between fluctuations mediated by fermions is obtained by inserting quaternions into the leading-order diagram. The re-summed box  is shaded grey. The first index of the matrix B denotes the type α = X/Y of entering spin fluctuations, and the second index the type of exiting spin fluctuations.
is shaded grey. The first index of the matrix B denotes the type α = X/Y of entering spin fluctuations, and the second index the type of exiting spin fluctuations.
However, the lowest-order diagrams alone can account only for the spectral shape whereas the variation of the intensity around Ts remains unexplained. To describe this aspect, we consider the interaction of fluctuations among themselves and with the lattice, all of which becomes crucial in the vicinity of the nematic transition19,20.
The interactions between spin fluctuations can be represented by a series of quaternion paramagnetic couplings mediated by fermions inserted into the leading-order Aslamazov–Larkin diagrams as shown in Fig. 3. The inserted fermionic boxes effectively resemble the dynamic nematic coupling constant g of the theory.
We have analysed the problem by extending SU(2) → SU(N) and taking the large N limit. For small frequencies Ω and in the large-N limit, after re-summing an infinite number of such box-like Aslamazov–Larkin diagrams, the Raman response function  reads:
reads:

Equation (1) states that the Raman response is proportional to the electronic contribution to the susceptibility of the nematic order parameter,

χmag(q) represents the magnetic susceptibility, which diverges at TSDW. For g ≠ 0 χnemel(0) has a Curie-like |T − T∗|−1 divergence at T∗ ≥ TSDW.
If the spins (or charges) couple to the lattice the susceptibility of the nematic order parameter is given by4,16,20

where λsl denotes the magneto-elastic coupling, and c0s is the bare elastic constant. Obviously, χnem(0) diverges at higher temperature than χnemel(0). We identify Ts ≥ T∗ with the structural transition and conclude that the Raman response (equation (1)) develops only a maximum rather than a divergence at Ts in agreement with the experiment here and recent theoretical work19,20.
Close to Ts, we expect equation (1) to hold qualitatively also inside the nematic phase, TSDW < T < Ts. We argue13 that χnemel(0) and, according to equation (1), the Raman amplitude are smaller than in the disordered (tetragonal) state but different from zero. This explains the continuous reduction of the Raman response of spin fluctuations on entering the nematic state. One can also show that the A1g response gets even further suppressed if one includes collisions between the fluctuations20.
As shown in equation (1) the full Raman response  is proportional to the bare response R0, μ(Ω) and to the electronic nematic susceptibility χnemel(0). Hence, the spectral shape is essentially given by R0, μ(Ω), which is therefore used in Fig. 2 to fit the data, whereas the intensity is dominated by the prefactor |T − T∗|−1. As the theoretical model is valid only in the limit of small frequencies we argue that the initial slope reflects the temperature dependence of the intensity and is proportional to χnemel(0), at least close to the transition. For generally reflecting the spectral shape above TSDW (equation (1)), R0, B1g(Ω, T) enables us to directly extract the initial slope of the experimental spectra by plotting R0, B1g(Ω, T)/Ω for all temperatures (Supplementary Information VI). These results are compiled in Fig. 4 along with the variation of χnemel(0, T) expected from mean-field theory. For low doping, we find qualitative agreement in the ranges T > TSDW. For higher doping the interactions between fluctuations become dominant and the mean-field prediction breaks down (Fig. 4c).
is proportional to the bare response R0, μ(Ω) and to the electronic nematic susceptibility χnemel(0). Hence, the spectral shape is essentially given by R0, μ(Ω), which is therefore used in Fig. 2 to fit the data, whereas the intensity is dominated by the prefactor |T − T∗|−1. As the theoretical model is valid only in the limit of small frequencies we argue that the initial slope reflects the temperature dependence of the intensity and is proportional to χnemel(0), at least close to the transition. For generally reflecting the spectral shape above TSDW (equation (1)), R0, B1g(Ω, T) enables us to directly extract the initial slope of the experimental spectra by plotting R0, B1g(Ω, T)/Ω for all temperatures (Supplementary Information VI). These results are compiled in Fig. 4 along with the variation of χnemel(0, T) expected from mean-field theory. For low doping, we find qualitative agreement in the ranges T > TSDW. For higher doping the interactions between fluctuations become dominant and the mean-field prediction breaks down (Fig. 4c).
a–c, The initial slope is given in arbitrary units because only the temperature dependence matters. The error bars in b represent the differences originating in the subtraction of the e–h continuum. They are large below Ts because of surface contaminations and smaller than the size of the points above. The grey curves in a,b represent |T − T∗|−1 with T∗ < Ts (see text).
The Raman response was also studied at various other doping levels in the range 0 ≤ x ≤ 0.085. Up to 6.1% Co substitution fluctuations were observed. In contrast to other publications14 we were not able to clearly identify and isolate the response of fluctuations at 8.5% although the kink in the B1g relaxation rate used to define Tf is clearly observed (Supplementary Fig. 4). The results for χnemel(0) up to 5.1% are unambiguous and are represented as a colour scale on the phase diagram in Fig. 5. Our phase diagram compares rather well to that derived from the elastic constant m66 (ref. 6). In addition, we show Tf up to x = 0.085. The fluctuations can be observed over a temperature range of approximately 70–100 K. This is more than in most of the other experiments on unstrained samples and comparable to what is found in the cuprates18,30.
The full lines limiting the nematic phase (magenta) and the blue squares representing the transition temperature Tc of superconducting samples were derived in ref. 22. Grey diamonds represent doping and temperature positions of the current Raman data. The coloured field between Ts and Tf represents the initial slope of the spectra according to the colour scale on the right. Tf is a crossover and corresponds to χnemel(0) → 0.
Methods
Samples.
The single crystals of undoped31 and Co-substituted Ba(Fe1−xCox)2As2 were grown using a self-flux technique and have been characterized elsewhere22. The cobalt concentration was determined by microprobe analysis. Ts and TSDW are close to 134 K in the undoped sample and cannot be distinguished. At nominally x = 0.025 we find Ts = 102.8 ± 0.1 K and TSDW = 98 ± 1 K by directly observing the appearance of twin boundaries and a symmetry-forbidden phonon line, respectively (see Supplementary Information I for details). The extremely sharp transition at Ts having ΔTs ≍ 0.2 K indicates that the sample is very homogeneous in the area of the laser spot.
Raman experiment.
The experiments were performed with standard light scattering equipment. For excitation either a solid-state laser (Coherent, Sapphire SF 532-155 CW) or an Ar ion laser (Coherent, Innova 300) was used emitting at 532 or 514.5 nm, respectively. The samples were mounted on the cold finger of a He-flow cryostat in a cryogenically pumped vacuum. The laser-induced heating was determined experimentally (see Supplementary Information I) to be close to 1 K per milliwatt of absorbed power. The spectra represent the response Rχμ′′(Ω, T) (μ = A1g, B1g, A2g and B2g), which is obtained by dividing the measured (symmetry resolved) spectra by the Bose–Einstein factor {1 + n(T, Ω)} = [1 − exp(−ℏΩ/kBT)]−1. χμ′′(Ω, T) is the imaginary part of the response function, and R is an experimental constant that connects the observed photon count rates with the cross-section and the van Hove function and accounts for units. For simplicity, the symmetry index μ is dropped in most of the cases. The symmetry selection rules refer to the 1 Fe unit cell (see Supplementary Fig. 1), which is more appropriate for electronic and spin excitations.
Static relaxation rates.
Static relaxation rates Γ0, μ(T), with μ denoting the symmetry, are used in various places (see, for example, Fig. 1b),

Γ0, μ(T) can be considered a symmetry-resolved ‘Raman resistivity’ that can be compared to, for example, transport data32. As the scattering intensity and consequently R are not known in absolute units Γ0, μ(T) cannot directly be derived. The problem was solved a while ago by adopting the memory function method33,34 for Raman scattering35. Then Γ0, μ(T) can be derived by extrapolating the dynamic Raman relaxation rates Γμ(Ω, T) to zero energy. More details can be found in Supplementary Information III.
References
Ando, Y., Segawa, K., Komiya, S. & Lavrov, A. N. Electrical resistivity anisotropy from self-organized one dimensionality in high-temperature superconductors. Phys. Rev. Lett. 88, 137005 (2002).
Borzi, R. A. et al. Formation of a nematic fluid at high fields in Sr3Ru2O7 . Science 315, 214–217 (2007).
Chu, J.-H. et al. In-plane resistivity anisotropy in an underdoped iron arsenide superconductor. Science 329, 824–826 (2010).
Chu, J.-H., Kuo, H.-H., Analytis, J. G. & Fisher, I. R. Divergent nematic susceptibility in an iron arsenide superconductor. Science 337, 710–712 (2012).
Fernandes, R. M., Chubukov, A. V. & Schmalian, J. What drives nematic order in iron-based superconductors? Nature Phys. 10, 97–104 (2014).
Kuo, H.-H., Chu, J.-H., Kivelson, S. A. & Fisher, I. R. Ubiquitous signatures of nematic quantum criticality in optimally doped Fe-based superconductors. Preprint at http://arXiv.org/abs/1503.00402 (2015).
Lederer, S., Schattner, Y., Berg, E. & Kivelson, S. A. Enhancement of superconductivity near a nematic quantum critical point. Phys. Rev. Lett. 114, 097001 (2015).
Baek, S.-H. et al. Orbital-driven nematicity in FeSe. Nature Mater. 14, 210–214 (2014).
Thorsmølle, V. K. et al. Critical charge fluctuations in iron pnictide superconductors. Phys. Rev. Lett. Preprint at http://arXiv.org/abs/1410.6456 (2014).
Gallais, Y., Paul, I., Chauviere, L. & Schmalian, J. Nematic resonance in the Raman response of iron-based superconductors. Preprint at http://arXiv.org/abs/1504.04570 (2015).
Capati, M. et al. Electronic polymers and soft-matter-like broken symmetries in underdoped cuprates. Nature Commun. 6, 7691 (2015).
Kamihara, Y., Watanabe, T., Hirano, M. & Hosono, H. Communication iron-based layered superconductor La[O1−x F x ]FeAs (x = 0.05–0.12) with T c = 26 K. J. Am. Chem. Soc. 130, 3296 (2008).
Fernandes, R. M., Chubukov, A. V., Knolle, J., Eremin, I. & Schmalian, J. Preemptive nematic order, pseudogap, and orbital order in the iron pnictides. Phys. Rev. B 85, 024534 (2012).
Gallais, Y. et al. Observation of incipient charge nematicity in Ba(Fe1−x Co x )2As2 . Phys. Rev. Lett. 111, 267001 (2013).
Kontani, H., Saito, T. & Onari, S. Origin of orthorhombic transition, magnetic transition, and shear-modulus softening in iron pnictide superconductors: analysis based on the orbital fluctuations theory. Phys. Rev. B 84, 024528 (2011).
Kontani, H. & Yamakawa, Y. Linear response theory for shear modulus C 66 and Raman quadrupole susceptibility: evidence for nematic orbital fluctuations in Fe-based superconductors. Phys. Rev. Lett. 113, 047001 (2014).
Caprara, S., Di Castro, C., Grilli, M. & Suppa, D. Charge-fluctuation contribution to the Raman response in superconducting cuprates. Phys. Rev. Lett. 95, 117004 (2005).
Caprara, S. et al. Signatures of nematic quantum critical fluctuations in the Raman spectra of lightly doped cuprates. Phys. Rev. B 91, 205115 (2015).
Khodas, M. & Levchenko, A. Raman scattering as a probe of nematic correlations. Phys. Rev. B 91, 235119 (2015).
Karahasanovic, U. et al. Manifestation of nematic degrees of freedom in the Raman response function of iron pnictides. Phys. Rev. B 92, 075134 (2015).
Yamase, H. & Zeyher, R. Spin nematic fluctuations near a spin-density-wave phase. New J. Phys. 17, 073030 (2015).
Chu, J.-H., Analytis, J. G., Kucharczyk, C. & Fisher, I. R. Determination of the phase diagram of the electron-doped superconductor Ba(Fe1−x Co x )2As2 . Phys. Rev. B 79, 014506 (2009).
Yoshizawa, M. et al. Structural quantum criticality and superconductivity in iron-based superconductor Ba(Fe1−x Co x )2As2 . J. Phys. Soc. Jpn 81, 024604 (2012).
Böhmer, A. E. et al. Nematic susceptibility of hole-doped and electron-doped BaFe2As2 iron-based superconductors from shear modulus measurements. Phys. Rev. Lett. 112, 047001 (2014).
Yi, M. et al. Symmetry-breaking orbital anisotropy observed for detwinned Ba(Fe1−x Co x )2As2 above the spin density wave transition. Proc. Natl Acad. Sci. USA 108, 6878–6883 (2011).
Mirri, C. et al. Hysteretic behavior in the optical response of the underdoped Fe-arsenide Ba(Fe1−x Co x )2As2 in the electronic nematic phase. Phys. Rev. B 89, 060501 (2014).
Lee, W.-C., Zhang, S.-C. & Wu, C. Pairing state with a time-reversal symmetry breaking in FeAs-based superconductors. Phys. Rev. Lett. 102, 217002 (2009).
Choi, K.-Y. et al. Self-energy effects and electron–phonon coupling in Fe–As superconductors. J. Phys. Condens. Matter 22, 115802 (2010).
Mazin, I. I. et al. Pinpointing gap minima in Ba(Fe0.94Co0.06)2As2 via band-structure calculations and electronic Raman scattering. Phys. Rev. B 82, 180502 (2010).
Muschler, B. et al. Electron interactions and charge ordering in CuO2 compounds. Eur. Phys. J. Spec. Top. 188, 131–152 (2010).
Rotter, M., Tegel, M. & Johrendt, D. Superconductivity at 38 K in the iron arsenide (Ba1−x K x )Fe2As2 . Phys. Rev. Lett. 101, 107006 (2008).
Devereaux, T. P. & Hackl, R. Inelastic light scattering from correlated electrons. Rev. Mod. Phys. 79, 175–233 (2007).
Götze, W. & Wölfle, P. Homogeneous dynamical conductivity of simple metals. Phys. Rev. B 6, 1226–1238 (1972).
Allen, J. W. & Mikkelsen, J. C. Optical properties of CrSb, MnSb, NiSb, and NiAs. Phys. Rev. B 15, 2952–2960 (1977).
Opel, M. et al. Carrier relaxation, pseudogap, and superconducting gap in high-T c cuprates: a Raman scattering study. Phys. Rev. B 61, 9752–9774 (2000).
Acknowledgements
We acknowledge useful discussions with T. P. Devereaux, Y. Gallais, S. A. Kivelson, B. Moritz and I. Paul. Financial support for the work came from the German Research Foundation DFG through the Priority Program SPP 1458 (project nos HA 2071/7 and SCHM 1035/5), from the Bavarian Californian Technology Center BaCaTeC (project no. A5 [2012-2]), and from the Transregional Collaborative Research Center TRR 80. U.K. and J.S. were supported by the Helmholtz Association, through the Helmholtz postdoctoral grant PD-075 ‘Unconventional order and superconductivity in pnictides’. R.H. thanks the Stanford Institute for Materials and Energy Sciences (SIMES) at Stanford University and SLAC National Accelerator Laboratory for hospitality. Work in the SIMES at Stanford University and SLAC was supported by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering, under Contract No. DE-AC02-76SF00515.
Author information
Authors and Affiliations
Contributions
F.K., T.B., B.M., A.B. and D.J. contributed approximately equally to the experiments. U.K., J.S., S.C., M.G. and C.D.C. developed the theory. J.-H.C., J.G.A. and I.R.F. prepared and characterized the samples. F.K., T.B. and R.H. conceived the study. U.K., F.K., T.B. and R.H. prepared the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 2478 kb)
Rights and permissions
About this article
Cite this article
Kretzschmar, F., Böhm, T., Karahasanović, U. et al. Critical spin fluctuations and the origin of nematic order in Ba(Fe1−xCox)2As2. Nature Phys 12, 560–563 (2016). https://doi.org/10.1038/nphys3634
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3634
This article is cited by
-
An electronic nematic liquid in BaNi2As2
Nature Communications (2022)
-
Quantum critical fluctuations in an Fe-based superconductor
Communications Physics (2022)
-
Lattice-shifted nematic quantum critical point in FeSe1−xSx
npj Quantum Materials (2021)
-
Nematic fluctuations in iron-oxychalcogenide Mott insulators
npj Quantum Materials (2021)
-
Strange semimetal dynamics in SrIrO3
Nature Communications (2020)