Abstract
The field of ‘Valleytronics’ has recently been attracting growing interest as a promising concept for the next generation electronics, because non-dissipative pure valley currents with no accompanying net charge flow can be manipulated for computational use, akin to pure spin currents1. Valley is a quantum number defined in an electronic system whose energy bands contain energetically degenerate but non-equivalent local minima (conduction band) or maxima (valence band) due to a certain crystal structure. Specifically, spatial inversion symmetry broken two-dimensional honeycomb lattice systems exhibiting Berry curvature is a subset of possible systems that enable optical2,3,4,5, magnetic6,7,8,9 and electrical control of the valley degree of freedom10,11,12. Here we use dual-gated bilayer graphene to electrically induce and control broken inversion symmetry (or Berry curvature) as well as the carrier density for generating and detecting the pure valley current. In the insulating regime, at zero-magnetic field, we observe a large nonlocal resistance that scales cubically with the local resistivity, which is evidence of pure valley current.
Similar content being viewed by others
Main
Charge and spin are both well-defined quantum numbers in solids. Spintronics is a technology that uses the spin degree of freedom. The application range of spintronics has been largely expanded by the development of electrical techniques for generating and detecting the spin current1. The valley degree of freedom in solid crystals can be handled by controlling the occupation of the non-equivalent structures in the band, providing the novel concept of so-called valleytronics.
Among various material candidates for valleytronics, two-dimensional (2D) honeycomb lattice systems with broken spatial inversion symmetry, such as gapped graphene and transition metal dichalcogenide (TMDC), are predicted to be the most useful. These systems have two valleys, called K and K′. Optical2,3,4,5, magnetic6,7,8,9 and electrical 10,11,12 control of the valley has been demonstrated. In particular, Berry curvature, which emerges in these honeycomb lattice systems with broken spatial inversion symmetry, enables electrical control of the valley degree of freedom.
Berry curvature acts as an out-of-plane pseudo-magnetic field in momentum space and has opposite sign between the two valleys. Therefore, a transverse pure valley current is generated by means of the anomalous velocity, in analogy to a transverse electronic current being generated by means of the Lorentz force due to a magnetic field in real space13,14 (see Fig. 1d). This phenomenon is called the valley Hall effect10 and can be used to generate a valley current. The inverse valley Hall effect, which converts the valley current into a transverse electric field, allows the detection of the pure valley current.
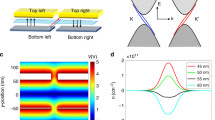
a, Band structure, Berry curvature and valley Hall conductivity of BLG. A band gap 2Δ and Berry curvature Ω emerge as a result of broken spatial inversion symmetry. The valley Hall conductivity σxyVH, which is calculated by integrating the Berry curvature, is constant in the bandgap. b, Schematic of the dual-gated BLG device. The top gate is a gold film, and the back gate is a p-doped silicon substrate. Two h-BN layers and a SiO2 film are used as gate insulators. Using these gates, the carrier density and perpendicular electric field (displacement field) are independently varied. Expanded image: Lattice structure of AB-stacked BLG. In the presence of a displacement field, an energy difference between the top and bottom layer emerges. Therefore spatial inversion symmetry is broken in this system, and both Berry curvature and a bandgap emerge. c, AFM image of the BLG device without the top h-BN. The light blue region indicates the area of the top gate. The BLG has a mobility of ∼15,000 cm2 V−1 s−1 at both 1.5 and 70 K. d, Schematic of the nonlocal resistance measurement and the nonlocal transport mediated by a pure valley current. The electric field driving the charge current in the left-hand circuit generates a pure valley current in the transverse direction by means of the valley Hall effect (VHE). This valley current is converted into an electric field or nonlocal voltage in the right-hand circuit by means of the inverse valley Hall effect (IVHE) to generate the nonlocal resistance.
The valley Hall effect was first reported for photo-generated electrons in monolayer MoS2 (ref. 11). However, the small inter-valley scattering length in this material prevents the detection of the pure valley current, which does not accompany the electronic current. Compared to TMDC, graphene has a much larger inter-valley scattering length owing to its higher crystal quality. Monolayer graphene on h-BN has more recently been used to generate and detect the pure valley current, where the crystal direction of the graphene was aligned to that of the h-BN such that the superlattice potential imposed by the h-BN structurally breaks the spatial inversion symmetry12. The valley Hall effect was analysed in detail with the carrier density as a parameter using metallic samples whose resistivity decreases as the temperature is lowered, but leaving unaddressed the insulating regime, which is more appropriate for investigating the pure valley current.
In this work we employed bilayer graphene (BLG) to generate and detect the valley current. We used a perpendicular electric field to break the spatial inversion symmetry and induce Berry curvature as well as a bandgap (see Fig. 1a). The dual-gated structure seen in Fig. 1b allows electrical and independent control of the perpendicular electric field and the carrier density15,16,17,18,19. This is in contrast to the monolayer graphene samples in ref. 12, where the monolayer graphene has to be structurally aligned with h-BN through a process of mechanical transfer. BLG valley Hall devices therefore show greater promise in terms of tunability of the valley current and applications to electronic devices. Indeed we show that independent control of the Fermi level and the bandgap enables us to prove the existence of the valley Hall effect in the insulating regime where the local resistivity increases with decreasing temperature. The significant advantage of the insulating system is that conversion from the electric field to the valley current is less dissipative than that in the metallic regime, as a much smaller current is injected. Such a regime has not been accessible with conventional spin or valley Hall systems.
In bilayer graphene with broken spatial inversion symmetry, the Berry curvature Ω and intrinsic valley Hall conductivity σxyVH are calculated as a function of the Fermi energy EF(refs 10,20,21):

and

where τz is the valley index (τz = −1 for K and +1 for K′), m is the effective mass in BLG without broken spatial inversion symmetry, e is the elementary charge, h is the Planck constant, and ℏ = h/2π. The Berry curvature Ω is defined only for |EF| ≥ Δ (half the bandgap, see Fig. 1a). σxyVH saturates at the maximum value 4e2/h when the Fermi level lies in the gap, because all occupied states in the valence band contribute to the valley Hall effect. Away from the gap—for example, when the Fermi energy lies above the gap—the conduction band, which has the opposite sign of Berry curvature to that of the valence band, contributes to reduce σxyVH.
To detect the pure valley current, the nonlocal resistance RNL was measured in the same scheme as is widely used in the spintronics field to detect pure spin current22,23,24,25,26. We observed a value of RNL at the charge neutrality point in the presence of a perpendicular electric field that was three orders of magnitude larger than the RNL due to the Ohmic contribution (explained later). We also found a cubic scaling relation between RNL and resistivity ρ (= 1/σxx), which is expected to appear when σxx is much larger than σxyVH in the intrinsic valley Hall effect. This cubic scaling was reproduced in multiple devices. From these findings we conclude that the origin of the observed large nonlocal resistance is the transport mediated by pure bulk valley current in a gapped state with electrically induced Berry curvature.
Figure 1b, c shows the schematic of the dual-gated BLG device and an AFM image of the device, respectively. BLG is encapsulated between two h-BN layers27 (see Methods) and gated through the h-BN layer from the top and from the bottom. The local and nonlocal resistance RL and RNL were derived from measurements of the four-terminal resistance Rij, kl, which is defined by the voltage between terminals i and j divided by the charge current injected between terminals k and l (see Fig. 1c, d). Unless mentioned, RL and RNL denote R57,38 and R45,67, respectively. The measurement was performed at 70 K using a low-frequency (around 1 Hz) lock-in technique, unless mentioned (see Methods and Supplementary Section I for details of the measurement).
Figure 2a, b shows the gate voltage dependence of RL and RNL, respectively. At the charge neutrality point (CNP), RL increases with the displacement field (D) (see Fig. 2a), reflecting the bandgap opening due to inversion symmetry breaking15,16,17,18,19,28. We found that RNL also increases with D around the CNP.
a,b, Gate voltage dependence of RL and RNL, respectively. The displacement fields from the back and top gate are defined as DBG = ɛBG(VBG − VBG0)/dBG and DTG = −ɛTG(VTG − VTG0)/dTG, respectively, where ɛBG(ɛTG) and dBG(dTG) are the relative dielectric constant and thickness of the back (top) gate, respectively and VBG0(VTG0) is the offset of the back (top) gate voltage under the top gated region due to environmental doping. The displacement field D is defined by the average of DBG and DTG.The red axis shows the scale of D. Inset: Schematic of the measurement configuration. The blue arrow shows the direction of charge flow. c, Comparison of the measured RNL (blue) with a calculation of the Ohmic contribution (magnified 1,000 times) (green). The RNL curve is extracted from the data along the direction of the green arrow in b at the highest D. The Ohmic contribution curve is calculated using the RL data along the direction of the green arrow in a at the highest D (see text).
In analogy with the spin Hall effect23 (Supplementary Section IX), RNL arising from the valley Hall and inverse valley Hall effects is given by

where σxyVH and lv are the valley Hall conductivity and the inter-valley scattering length, respectively. W and L are the width and length of the Hall bar channel. Local conductivity σxx is minimized at the CNP and with increasing D, thus enhancing RNL (equation (3)). For a given D, RNL is further maximized around the CNP owing to the maximal valley Hall conductivity σxyVH (equation (2)). We confirmed that RNL is unchanged when swapping the measurement terminals—that is, R45,67 ∼ R67,45 (Supplementary Section II). We also consider a contribution of trivial Ohmic resistance which is due to classical diffusive charge transport to the measured nonlocal resistance. The Ohmic contribution can be calculated using the van der Pauw formula RNL = ρ/πexp(−π(L/W)) (refs 12,24,25,26), where we define the resistivity ρ = RL(W/L), and is compared with the measured nonlocal resistance in Fig. 2c. The measured RNL is three orders of magnitude larger than the calculated Ohmic contribution. We therefore exclude the Ohmic contribution as the origin of the observed RNL.
In the gapped BLG, the electron conduction mechanism depends on the temperature T. At high T it is dominated by thermal activation across the bandgap, namely band transport, whereas at low T it is dominated by hopping conduction between impurity states15,17,18,19.
The temperature dependence of maximum ρ with respect to carrier density (ρmax) was measured for various displacement fields D (Fig. 3a, inset). We plot 1/ρmax as a function of 1/T for D = 0.55 V nm−1 as a typical example in Fig. 3a. The temperature dependence is strong at high T (> 79 K), reflecting band conduction, and weak at low T, reflecting hopping conduction. The temperature dependence over the whole range is reproduced well by a double exponential function:

where E1L (E2L) and ρ1 (ρ2) are the activation energy and the local resistivity, respectively for the high-T (low-T) regime. 2E1L indicates the bandgap size, and is around 80 meV at the highest D (Supplementary Section IV). The crossover temperature Tc between the high- and low-temperature regions is determined by the crossing point of the first and second term of equation (4), as shown in Fig. 3a. The temperature dependence of the maximum nonlocal resistance RNLmax was also measured (Fig. 3b, inset) and analysed with the following fitting function in the same way as for ρmax, as shown in Fig. 3b:

where E1NL (E2NL) is the activation energy and R1 (R2) is a fitted proportionality factor, respectively, for the high-T (low-T) regime. The temperature dependence is fairly similar to that of ρmax in Fig. 3a. We also plot the crossover temperature Tc for both 1/ρmax and 1/RNLmax as a function of D in Fig. 3c. The Tc for 1/ρmax divides the D–T plane into the band conduction region (light green) and the hopping conduction region (light red).
a,b, Typical data fitting using a double exponential function for 1/ρmax (a) and 1/RNLmax (b). The blue broken curve indicates the fitting curve. The green (red) line indicates the contribution from band (hopping) conduction. The crossover temperature Tc is defined by the crossing of the two lines. Inset: Temperature dependence of maximum ρ (a) and RNL (b) with respect to the carrier density. D is varied from 0.85 V nm−1 (red) to 0.01 V nm−1 (purple) in a and from 0.85 V nm−1 (red) to 0.17 V nm−1 (blue) in b with a constant interval. c, Tc derived from the data fitting as in a for 1/ρmax and b for 1/RNLmax. The error bars are due to the accuracy of the fitting. The light green (red) area is the region of band conduction (hopping conduction). The blue curve shows the fitting result for the nonlocal 1/Tc versus 1/D.
The critical temperatures Tc of 1/ρmax and 1/RNLmax coincide for D > 0.4 V nm−1, indicating that there is correlation of the crossover behaviour between the local and nonlocal transport. However, it deviates for D < 0.4 V nm−1 for the following two possible reasons. The first possible reason is underestimation of the Tc of the nonlocal transport in the low-D region. The nonlocal voltage becomes very small at high T and low D, making precise measurement of RNL difficult. In this regime, there are fewer measured points available for the fitting, resulting in the underestimation of Tc. The second possible reason is that the nonlocal transport by the valley current is less affected by charge puddles compared to the local transport, although we do not yet fully understand the reason for this observation.
One noticeable result is that the Tc of the nonlocal transport depends almost linearly on D for the entire region in Fig. 3c (see the blue curve; Supplementary Section V). This behaviour may indicate that the Tc is affected by the size of bandgap but less affected by the size of potential fluctuations due to charge puddles. Note that all four of the fitting parameters in equations (4) and (5) have a D dependence; therefore, obtaining an analytical relationship between D and Tc is not straightforward.
Another notable result is that the high-T activation energy E1 is different between the local and nonlocal transport (Supplementary Sections IV and V, see Supplementary Figs 7 and 8). This already implies there is no linear relation between RNL and ρ in our device. This observation is in contrast to a previous report on monolayer graphene12, where both activation energies were similar.
We now present the scaling relation between ρ and RNL at the CNP. Figure 4 is a plot of RNL versus ρ obtained for various displacement fields D. The crossover behaviour between the band conduction and the hopping conduction shows up again on this plot. In the band conduction region (ρ < 7 kΩ) we observe a clear cubic scaling relation (green line), whereas we observe saturation in the hopping conduction region (ρ > 7 kΩ). Similar cubic and saturating scaling relations are obtained for different physical conditions. The ρ versus RNL relation obtained for different carrier densities and temperatures at fixed displacement fields are shown in Supplementary Sections VI and VII, respectively. In addition, we observe a similar scaling relation for multiple devices (see Fig. 4 inset for one example).
Each data point is extracted from Fig. 2a, b for a different D value ranging from 0.22 to 0.85 V nm−1 at CNP. Inset: Scaling relation between the maximum ρ(ρmax) and RNL(RNLmax) as functions of the carrier density obtained from various D ranging from 0.51 to 0.75 V nm−1 (red points) and −0.50 to −0.76 V nm−1 (blue points) in another dual-gated bilayer graphene Hall bar device. The width and length of the Hall bar channel are 1 μm and 4.5 μm, respectively. Measurement was performed at 50 K. At lower temperatures, we also observed deviation from the cubic scaling for high displacement fields.
By assuming a constant inter-valley scattering length and replacing σxx with ρ−1 in equation (3), we derive the following scaling relation between RNL and ρ:

The cubic scaling between RNL and ρ holds for the constant valley Hall conductivity which is expected when the Fermi level is in the bandgap or near the CNP (see Fig. 1a) for the intrinsic valley Hall effect, σxyVH = 4e2/h. The observed cubic relation for small D in Fig. 4 is therefore consistent with the theoretical expectation, providing unambiguous evidence of the valley transport. Note that, at finite temperatures, σxyVH is reduced from 4e2/h. However, in the range of displacement fields used here, it stays almost constant with a value close to 4e2/h (see Supplementary Section X).
Using σxyVH = 4e2/h and substituting σxx = ρ−1 and the sample dimensions into equation (3), we obtain lv = 1.6 μm. This is comparable to the estimated inter-valley scattering length in previous works12,29. By using different sets of four terminals we observed a significantly increasing decay of RNL with L (Supplementary Section V), probably owing to valley relaxation due to edge scattering, as discussed in a weak localization study29.
We here note that equations (3) and (6) are valid only for σxx ≫ σxyVH (Supplementary Section IX). Otherwise we need to solve the conductance matrix and the diffusion equation of the entire Hall bar in a self-consistent way. Indeed, deviation from the cubic scaling in the large-D region observed in Fig. 4 may arise owing to the inapplicability of equations (3) and (6). However, it does not account for the saturation of RNL for large ρ (Supplementary Section IX). Another possible scenario to account for the saturation of RNL is the crossover of the conduction mechanism, as discussed in Fig. 3c. In studies of the anomalous Hall effect, the crossover between the metallic and the hopping transport regime has been experimentally studied, and the scaling relation σxy ∝ σxx1.6 has been reported in a wide range of materials13. If we apply this experimental rule for equation (6), we find RNL to be almost constant with ρ. Here, we are again cautious about the validity of equation (6) in this argument, because in the saturation region σxx < σxyVH for σxyVH = 4e2/h. However, by including extrinsic contributions—for example, the side-jump contribution10—σxyVH can be smaller than 4e2/h and σxx. In such a case, we can keep the above-described analogy with the anomalous Hall effect. Further experimental and theoretical investigations are needed into the valley Hall effect in the insulating regime30, where conventional formulae are not applicable.
We finally exclude another scenario that might account for the RNL observed here. In the gap of bilayer graphene, the presence of localized states along the edge resulting from the topological property of BLG has been predicted theoretically31. This might also contribute to the nonlocal transport. With a large displacement field or large bandgap, the bulk shunting effect is small and the conduction becomes dominated by the edge transport. In such a case, RNL should be proportional to the local resistance obtained by a four-terminal measurement (Supplementary Section X). This linear scaling does not fit any of the observed features (demonstrated in Fig. 4). We draw a linear scaling line in blue in Fig. 4, but this does not fit any of the observed features. Even when we consider the effect of bulk shunting, we find that the scaling is far from the cubic line (Supplementary Section X). So we exclude the possibility of edge transport as the origin of the observed RNL and conclude that it comes from the bulk valley current in the gap. Also the transport through the localized states along the edge was disproved by the measurement on a Corbino geometry device19.
We used a dual-gated BLG in the Hall bar geometry to electrically control the broken inversion symmetry of BLG, and hence the valley degree of freedom. We observed a large nonlocal resistance in the insulating regime at 70 K and revealed a cubic scaling between the nonlocal resistance and the local conductivity as an indication of pure valley current flow. The valley current is fully controlled by electrical gating, with the bandgap, the Fermi level and broken inversion symmetry as parameters. This will allow further studies on the underlying physics of the valley current, in particular for σxx < σxyVH, as well as applications for non-dissipative electronic devices. While preparing the manuscript, observation of the topological valley current along an AB–BA stacking domain wall in bilayer graphene has been reported32. This topological valley current along the domain wall also originates from the non-zero valley Hall conductivity (or non-zero valley Chern number) in the gap of bilayer graphene with broken spatial inversion symmetry.
Note added in proof:
We became aware that there is similar work related to valley current transport in dual-gated bilayer graphene33.
Methods
We used a mechanical exfoliation technique to prepare bilayer graphene (BLG) and h-BN flakes. The number of layers in each graphene flake on the SiO2/Si substrate was identified by optical contrast. The SiO2 was 285 nm thick, the Si was heavily p-doped and used for back gating. We transferred the BLG flakes onto h-BN flakes prepared on SiO2 using the PMMA transfer technique reported in ref. 34. Then Ti/Au (10 nm/190 nm) was deposited to make Ohmic contacts. BLG was etched into a Hall bar by means of an Ar plasma. After each transfer and lithography step, except for the step between the Ohmic contact deposition and Ar plasma etching, the device was annealed at 300 °C in an Ar/H2 atmosphere for a few hours to remove the resist residue. However, the PMMA residue could not be completely removed by annealing, so we used a mechanical cleaning technique35,36,37 utilizing an AFM in tapping mode. After shaping the Hall bar, an h-BN flake was transferred to the top of the BLG/h-BN stacking layer. Finally, Ti/Au (10 nm/190 nm) was deposited onto the h-BN/BLG/h-BN stacking layer to make the top gate. The thicknesses of the top and bottom h-BN layers measured by AFM were 21 nm and 35 nm, respectively.
Measurements were made using a low-frequency (around 1 Hz) lock-in technique. We found that current leakage through the input impedance of the voltage amplifiers causes an artefact in the nonlocal measurement. However, by using a simple circuit model, we confirmed that the error was not significant in this measurement (see Supplementary Section I). For the measurement shown in the inset of Fig. 4, we used home-made voltage amplifiers with a high input impedance to suppress the artefact further.
References
Jungwirth, T., Wunderlich, J. & Olejník, K. Spin Hall effect devices. Nature Mater. 11, 382–390 (2012).
Yao, W., Xiao, D. & Niu, Q. Valley-dependent optoelectronics from inversion symmetry breaking. Phys. Rev. B 77, 235406 (2008).
Cao, T. et al. Valley-selective circular dichroism of monolayer molybdenum disulphide. Nature Commun. 3, 887 (2012).
Zeng, H., Dai, J., Yao, W., Xiao, D. & Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nature Nanotech. 7, 490–493 (2012).
Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nature Nanotech. 7, 494–498 (2012).
Li, Y. et al. Valley splitting and polarization by the Zeeman effect in monolayer MoSe2 . Phys. Rev. Lett. 113, 266804 (2014).
MacNeill, D. et al. Breaking of valley degeneracy by magnetic field in monolayer MoSe2 . Phys. Rev. Lett. 114, 037401 (2015).
Srivastava, A. et al. Valley Zeeman effect in elementary optical excitations of monolayer WSe2 . Nature Phys. 11, 141–147 (2015).
Aivazian, G. et al. Magnetic control of valley pseudospin in monolayer WSe2 . Nature Phys. 11, 148–152 (2015).
Xiao, D., Yao, W. & Niu, Q. Valley-contrasting physics in graphene: Magnetic moment and topological transport. Phys. Rev. Lett. 99, 236809 (2007).
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014).
Gorbachev, R. V. et al. Detecting topological currents in graphene superlattices. Science 346, 448–451 (2014).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Oostinga, J. B., Heersche, H. B., Liu, X., Morpurgo, A. F. & Vandersypen, L. M. K. Gate-induced insulating state in bilayer graphene devices. Nature Mater. 7, 151–157 (2007).
Zhang, Y. et al. Direct observation of a widely tunable bandgap in bilayer graphene. Nature 459, 820–823 (2009).
Zou, K. & Zhu, J. Transport in gapped bilayer graphene: The role of potential fluctuations. Phys. Rev. B 82, 081407 (2010).
Taychatanapat, T. & Jarillo-Herrero, P. Electronic transport in dual-gated bilayer graphene at large displacement fields. Phys. Rev. Lett. 105, 166601 (2010).
Yan, J. & Fuhrer, M. S. Charge transport in dual gated bilayer graphene with Corbino geometry. Nano Lett. 10, 4521–4525 (2010).
Koshino, M. Electronic transport in bilayer graphene. New J. Phys. 11, 095010 (2009).
Zhang, F., Jung, J., Fiete, G. A., Niu, Q. & MacDonald, A. H. Spontaneous quantum Hall states in chirally stacked few-layer graphene systems. Phys. Rev. Lett. 106, 156801 (2011).
Valenzuela, S. O. & Tinkham, M. Direct electronic measurement of the spin Hall effect. Nature 442, 176–179 (2006).
Abanin, D. A., Shytov, A. V., Levitov, L. S. & Halperin, B. I. Nonlocal charge transport mediated by spin diffusion in the spin Hall effect regime. Phys. Rev. B 79, 035304 (2009).
Brüne, C. et al. Evidence for the ballistic intrinsic spin Hall effect in HgTe nanostructures. Nature Phys. 6, 448–454 (2010).
Abanin, D. A. et al. Giant nonlocality near the Dirac point in graphene. Science 332, 328–330 (2011).
Balakrishnan, J., Koon, G. K. W., Jaiswal, M., Neto, A. H. C. & Özyilmaz, B. Colossal enhancement of spin–orbit coupling in weakly hydrogenated graphene. Nature Phys. 9, 284–287 (2013).
Dean, C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nature Nanotech. 5, 722–726 (2010).
Ohta, T., Bostwick, A., Seyller, T., Horn, K. & Rotenberg, E. Controlling the electronic structure of bilayer graphene. Science 313, 951–954 (2006).
Tikhonenko, F. V., Horsell, D. W., Gorbachev, R. V. & Savchenko, A. K. Weak localization in graphene flakes. Phys. Rev. Lett. 100, 056802 (2008).
Lensky, Y. D., Song, J. C. W., Samutpraphoot, P. & Levitov, L. S. Topological valley currents in gapped Dirac materials. Phys. Rev. Lett. 114, 256601 (2015).
Li, J., Martin, I., Büttiker, M. & Morpurgo, A. F. Topological origin of subgap conductance in insulating bilayer graphene. Nature Phys. 7, 38–42 (2010).
Ju, L. et al. Topological valley transport at bilayer graphene domain walls. Nature 520, 650–655 (2015).
Sui, M. et al. Gate-tunable topological valley transport in bilayer graphene. Nature Phys. http://dx.doi.org/10.1038/nphys3485 (2015).
Taychatanapat, T., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Quantum Hall effect and Landau-level crossing of Dirac fermions in trilayer graphene. Nature Phys. 7, 621–625 (2011).
Jalilian, R. et al. Scanning gate microscopy on graphene: Charge inhomogeneity and extrinsic doping. Nanotechnology 22, 295705 (2011).
Goossens, A. M. et al. Mechanical cleaning of graphene. Appl. Phys. Lett. 100, 073110 (2012).
Lindvall, N., Kalabukhov, A. & Yurgens, A. Cleaning graphene using atomic force microscope. J. Appl. Phys. 111, 064904 (2012).
Acknowledgements
We acknowledge fruitful discussion with L. S. Levitov, J. C. W. Song, M. Koshino, M. Ezawa and N. Nagaosa. Y.S. acknowledges support from Japan Society for the Promotion of Science (JSPS) Research Fellowship for Young Scientists and JSPS Program for Leading Graduate Schools (MERIT). M.Y., K.W. and T.T. acknowledge support from JSPS Grant-in-Aid for Scientific Research on Innovative Areas ‘Science of Atomic Layers’. M.Y. acknowledges support from Canon Foundation. I.V.B. acknowledges support from JSPS International Research Fellowship. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan. T.T. acknowledges support from JSPS Grant-in-Aid for Scientific Research A (No. 26248061) and JSPS Innovative Areas ‘Nano Informatics’ (No. 25106006). S.T. acknowledges support from DFG-JST joint research project ‘Topological Electronics’ and JSPS Grant-in-Aid for Scientific Research S (No. 26220710).
Author information
Authors and Affiliations
Contributions
Y.S. conceived the experiment, designed the experiment with M.Y., fabricated the samples, conducted measurements and analysis, interpreted the data with M.Y., and wrote the manuscript with M.Y., I.V.B. and S.T. I.V.B. contributed to the measurements. T.T. and K.W. synthesized h-BN samples. M.Y. and S.T. directed the research. All authors discussed the results and the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 3160 kb)
Rights and permissions
About this article
Cite this article
Shimazaki, Y., Yamamoto, M., Borzenets, I. et al. Generation and detection of pure valley current by electrically induced Berry curvature in bilayer graphene. Nature Phys 11, 1032–1036 (2015). https://doi.org/10.1038/nphys3551
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3551
This article is cited by
-
Inheritance of the exciton geometric structure from Bloch electrons in two-dimensional layered semiconductors
Frontiers of Physics (2024)
-
Quantized valley Hall response from local bulk density variations
Communications Physics (2023)
-
Non-identical moiré twins in bilayer graphene
Nature Communications (2023)
-
Interlayer exciton dynamics of transition metal dichalcogenide heterostructures under electric fields
Nano Research (2023)
-
Strain engineering of electronic properties and anomalous valley hall conductivity of transition metal dichalcogenide nanoribbons
Scientific Reports (2022)