Abstract
The properties of two-dimensional transition metal dichalcogenides arising from strong spin–orbit interactions and valley-dependent Berry curvature effects have recently attracted considerable interest1,2,3,4,5,6,7. Although single-particle and excitonic phenomena related to spin–valley coupling have been extensively studied1,3,4,5,6, the effects of spin–valley coupling on collective quantum phenomena remain less well understood. Here we report the observation of superconducting monolayer NbSe2 with an in-plane upper critical field of more than six times the Pauli paramagnetic limit, by means of magnetotransport measurements. The effect can be interpreted in terms of the competing Zeeman effect and large intrinsic spin–orbit interactions in non-centrosymmetric NbSe2 monolayers, where the electron spin is locked to the out-of-plane direction. Our results provide strong evidence of unconventional Ising pairing protected by spin–momentum locking, and suggest further studies of non-centrosymmetric superconductivity with unique spin and valley degrees of freedom in the two-dimensional limit.
Similar content being viewed by others
Main
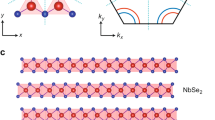
Monolayer transition metal dichalcogenide (TMD) of the hexagonal structure consists of a layer of transition metal atoms sandwiched between two layers of chalcogen atoms in the trigonal prismatic structure8 (Fig. 1a). It possesses out-of-plane mirror symmetry and broken in-plane inversion symmetry. The presence of 4d transition metal also gives rise to large spin–orbit interactions (SOIs). The mirror symmetry restricts the crystal field (ɛ) to the plane. The SOIs split the spin states at finite momentum k in the absence of inversion symmetry. They manifest as an effective magnetic field HSO(k) along the direction of k × ɛ, which is out of plane for the restricted two-dimensional (2D) motion of electrons in the plane. The electron spin is thus oriented in the out-of-plane direction and in opposite directions for electrons of opposite momenta1,2,3 (Fig. 1a). Such spin–momentum locking is destroyed in the bulk where inversion symmetry and spin degeneracy are restored1,2,7 (Fig. 1b). New valley- and spin-dependent phenomena including optical orientation of the valley polarization3,4 and the valley Hall effect5 have been recently demonstrated in group-VI TMD monolayers such as MoS2. The effect of spin–momentum locking on collective quantum phenomena in monolayer TMDs, however, remains an open area.
a,b, Illustration of spin–momentum locking in monolayer (a) and spin–layer locking in bilayer/bulk (b) NbSe2. First row: monolayer NbSe2 consists of a layer of Nb atoms (blue balls) sandwiched between two layers of Se atoms (yellow balls) in the trigonal prismatic structure. Bulk 2H-NbSe2 is made of monolayers stacked in the ABAB…sequence. Second row: Brillouin zone in the in-plane direction and Fermi surface near the Γ, K and K′ point. The Fermi surface is spin split in the monolayer and is spin degenerate in the bilayer/bulk. c, Optical image of a bilayer NbSe2 device capped by a thin h-BN layer for environmental protection. The scale bar corresponds to 5 μm. Current was excited through electrode S and D; voltage drop was measured across A and B. d, Temperature dependence of the normalized four-point resistance R for a typical bulk, bilayer and monolayer NbSe2 device from 2.1 to 300 K.
In this work, we demonstrate very high in-plane upper critical fields induced by spin–momentum locking in superconducting monolayers of group-V TMD niobium diselenide (NbSe2). This was achieved through transport and magnetotransport studies of high-quality NbSe2 devices of varying layer thickness. Bulk 2H-NbSe2 is a well-studied type II anisotropic multiband superconductor with a zero-field critical temperature TC0 ≈ 7 K (refs 9,10,11,12,13,14). Superconductivity in atomically thin NbSe2 (refs 15,16) and samples down to the monolayer thickness17,18 has also been observed recently. Monolayer NbSe2 can be viewed as heavily hole-doped monolayer MoSe2 (refs 8,19): the Fermi surface is composed of one pocket at the Γ point and two pockets at the K and the K′ point of the Brillouin zone with each pocket spin split into two pockets by the SOIs (ref. 19; Fig. 1a); the spin splitting around the Γ point is much smaller than that at the K (K′) point19 and the spin–momentum locking effects are dominated by the K (K′) pockets.
In conventional superconductors, superconductivity can be quenched under a sufficiently high external magnetic field by the orbital11,20 and spin Zeeman effect21,22. They are originated from the coupling between the electron momentum and the magnetic field (for example, vortex formation) and from spin alignment by the magnetic field, respectively. In the limit of monolayer thickness, the interlayer coupling vanishes and the orbital effect is absent for an in-plane magnetic field H∥. The in-plane upper critical field (critical field at zero temperature) Hc20∥ is thus determined by direct spin-flip, known as the Pauli paramagnetic limit HP ≈ 1.84 TC0 (in tesla for TC0 in kelvin) for isotropic BCS superconductors21,22. Under this field the Zeeman splitting energy matches the superconducting energy gap, or equivalently, the binding energy of a Cooper pair. Spin–momentum locking and the consequent pairing of the K and K′ electrons with spin locked to the two opposite out-of-plane directions (Fig. 1a), referred to as Ising pairing, is expected to significantly enhance the in-plane paramagnetic field23,24,25 in monolayer NbSe2.
In our experiment, we fabricated monolayer and few-layer samples of NbSe2 by mechanical exfoliation of 2H-NbSe2 single crystals followed by direct transfer onto SiO2/Si substrates with pre-patterned electrodes and encapsulation by thin layers of hexagonal boron nitride (see Methods). The sample thickness was determined with monolayer accuracy by optical spectroscopy, particularly, the frequency shift of the interlayer shear mode17. The crystal symmetry is characterized by optical second-harmonic generation. (See Supplementary Section 1 for details on optical characterization.) Figure 1c is an optical image of a representative device (bilayer in this case). The temperature dependence of the normalized four-point resistance R(T)/R(300 K) at zero magnetic field is shown in Fig. 1d from 2 to 300 K for a typical bulk, bilayer and monolayer device. (See Supplementary Section 2 for original data and more devices.) All samples show a metallic behaviour with phonon-limited transport at high temperature (with R ∝ T) and disorder-limited transport at low temperature (with R approaching a constant value) before reaching the superconducting state. The residual resistance ratio evaluated using the room-temperature resistance and the normal-state resistance right above the superconducting transitionRn (taken at 8 K) varies from ∼30 in the bulk to ∼10 in the monolayer device. The square resistance per layer (at 8 K) was estimated to be ≈ 200 Ω for the bilayer of Fig. 1c and similar values were estimated for other devices. These values are much smaller than h/4e2 ≈ 6,450 Ω, where a disorder-induced superconductor–insulator transition emerges26. Here e is the electron charge and h is the Planck constant. Our samples are therefore in the low-disorder regime compared with similar layered compounds studied previously16 and the disorder effects on TC0 are expected to be small26.
Figure 2a shows the temperature dependence near the superconducting transition of the resistance normalized by Rn for NbSe2 samples of varying thickness N. Superconductivity is observed for all samples down to the monolayer thickness. A significant drop in the transition temperature accompanied with a significant broadening is observed for N < 4 (∼2.6 nm). The broadening can be attributed to enhanced thermal fluctuations in two dimensions20,27 when the sample thickness falls below the bulk out-of-plane coherence length of 2.7 nm (ref. 10). We have used the Aslamazov–Larkin formula28 to determine TC0 (solid lines, Fig. 2a), which is close to the temperature corresponding to 0.5Rn. We have also performed current excitation measurements to investigate the importance of phase fluctuations, and the Berezinskii–Kosterlitz–Thouless transition temperature27 is found to be close to T(0.01Rn). Figure 2b summarizes the N-dependence of TC0, T(0.5Rn) and T(0.01Rn). The monotonic dependence of TC0 on N can be accounted for by the decreasing interlayer Cooper pairing29,30 (as evidenced by the linear dependence of [ln(TC0(N)) − ln(TC0(N = 1))]−1 on [cos(π/(N + 1))]−1 in the inset of Fig. 2b). Effects on TC0 from the competing charge-density-wave order, which is enhanced with decreasing N, are thus likely to be weak in NbSe2 (ref. 14). (See Supplementary Sections 3 and 4 for details on the study of the characteristics of 2D superconductivity in NbSe2).
a, Temperature dependence of the resistance for NbSe2 samples of varying thickness N. The resistance is normalized to the normal-state value right above the superconducting transition. The solid lines are fits to the Aslamazov–Larkin formula for R(T)/Rn > 0.5. b, Layer number N dependence of T(0.5Rn),T(0.01Rn), and TC0. The inset shows the dependence of [ln(TC0(N)) − ln(TC0(N = 1))]−1 on[cos(π/(N + 1))]−1 (symbols), where TC0(N = 1) ≈ 3.0 K. Dashed lines are the best fit to a linear dependence (inset) and its representation as TC0(N).
With the above understanding of the nature of superconductivity in 2D NbSe2, we now study its magnetic response. Figure 3a–c shows the temperature dependence of the four-point resistance for a bulk, trilayer and monolayer sample under both out-of-plane (H⊥) and in-plane magnetic fields (H∥). A second monolayer device with two-point measurements up to 20 T is also included. For all samples, we normalize the temperature by the corresponding TC0, and the resistance by Rn. We define the critical temperature TC under a finite magnetic field Hc2 as the temperature corresponding to 50% of Rn, in accordance with the zero-field convention. For two-point measurements, as shown in Fig. 3c, we assign TC0 as the temperature at which a rapid resistance drop occurs while the sample is cooled from the normal state. It is clear that for all samples superconductivity is more susceptible to H⊥ than to H∥ and the magnetic anisotropy is significantly larger in atomically thin samples than in the bulk. (For the angular dependence study of the magnetic response refer to Supplementary Section 5.)
a–c, Temperature dependence of the d.c. resistance for a bulk (a), trilayer (b) and monolayer (c) NbSe2 device under out-of-plane (H⊥, top row) and in-plane (H∥, bottom row) magnetic fields. The inset of c shows the two-point resistance of a second monolayer device under in-plane magnetic fields. The crossing of the two dashed lines is used to determine TC. Devices are labelled by their numbers.
We summarize the Hc2–TC phase diagram for differing sample thickness N in Fig. 4 for both H⊥ (open symbols) and H∥ (filled symbols). For comparison, we normalize the critical field Hc2 by the BCS Pauli paramagnetic limit HP and the critical temperature TC by TC0 for each sample. For out-of-plane fields, our experiment shows a linear Hc2⊥–TC dependence that is largely thickness independent. The result can be explained by considering the orbital effect, that is, overlaps of vortex cores, as the major quenching mechanism. Hc20⊥ is determined by the combined effect of in-plane coherence length and transport mean free path20. Whereas the coherence length increases with reducing thickness (because of the reduction in TC0), the mean free path decreases as the material becomes more disordered. The net effect is a weak Hc2⊥–TC dependence on N. The measured upper critical field for bulk NbSe2Hc20⊥ ≈ 4 T (≪HP) agrees well with the reported value9,10.
The critical field Hc2/HP as a function of transition temperature TC/TC0 for NbSe2 samples of differing thickness under both out-of-plane H⊥ (open symbols) and in-plane H∥ (filled symbols) magnetic fields. Filled circles and triangles represent data acquired from different devices (see Supplementary Section 2). The dashed line corresponds to the Pauli paramagnetic limit. The solid blue line is the best fit to the solution of the pair breaking equation. The solid green line is a linear fit. The inset shows the zero-bias peak area and width as a function of H∥ at 0.36 K obtained from differential conductance measurements in a monolayer device. The result shows that superconductivity in monolayer NbSe2 survives under H∥ = 31.5 T.
In contrast, for in-plane fields, the Hc2∥–TC dependence near TC0 in the monolayer is much steeper than in the bulk and follows a square root instead of a linear dependence. More significantly, the monolayer upper critical field Hc20∥ far exceeds its Pauli limit HP whereas Hc20∥ ≳ HP in the bulk. We note that large enhancements of Hc20∥ (≫HP) have been observed in other systems9,31,32,33,34,35 including two recent experiments on MoS2 crystals gated by ionic liquids36,37. Many mechanisms have been discussed including strong coupling38,39, modified electron g-factor20,23, interaction effects38,40,41, remnant magnetic susceptibility at low temperatures20,21,22, spin–orbit scattering from impurities31,32,42,43,44 and intrinsic SOIs (refs 23,24,25,35,36,37). The observed large enhancement of Hc20∥ in monolayer NbSe2 can be understood as a special case of intrinsic SOI effects predicted for non-centrosymmetric superconductors23,24,25. In particular, the relevant spin–orbit field for monolayer NbSe2 with D3h symmetry can be derived following refs 23,25

Here H0 is the magnitude of the spin–orbit field at the K (K′) point, a = 0.35 nm (ref. 8) is the in-plane lattice constant, and  denotes the out-of-plane unit vector. As mentioned above, the field at the K (K′) pocket far exceeds that around the Γ pocket19 and dominates the magnetic field response of superconductivity. Neglecting trigonal warping, the spin–orbit field at the Fermi surface for the K (or K′) pocket is approximately a constant
denotes the out-of-plane unit vector. As mentioned above, the field at the K (K′) pocket far exceeds that around the Γ pocket19 and dominates the magnetic field response of superconductivity. Neglecting trigonal warping, the spin–orbit field at the Fermi surface for the K (or K′) pocket is approximately a constant  (or
(or  ) with HSO ≲ H0.
) with HSO ≲ H0.
In the absence of the orbital effect, Hc20∥ is determined by the alignment of spin by the external field. The upper critical field can be estimated by noting that the in-plane component of the spin magnetic moment is reduced to ∼(H∥/HSO)μB with μB denoting the Bohr magneton. The ratio H∥/HSO originates from a competition between HSO, which locks the electron spin to the out-of-plane direction, and H∥, which tilts the spin towards the in-plane direction25. Pair breaking occurs when the modified Zeeman energy ∼(H∥2/HSO)μB (known as van Vleck paramagnetism24,25) overcomes the superconducting gap (that is, (H∥2/HSO)μB ∼ HPμB). It thus yields the following estimate for  , which can greatly exceed HP if HSO ≫ HP for strong SOIs.
, which can greatly exceed HP if HSO ≫ HP for strong SOIs.
To analyse the entire Hc2∥–TC phase diagram, we introduce the pair breaking equation20 for monolayer NbSe2 with the spin–momentum locking effect incorporated

Here ψ(x) is the digamma function. Near TC0, equation (2) can be reduced to (1 − (TC/TC0)) = ((Hc2∥)2/HSOHP), which describes well the observed square-root dependence of  . We fit the experimental Hc2∥ − TC dependence to the solution of equation (2) with HSO as a free parameter. The best fit (blue line, Fig. 4) gives the spin–orbit field HSO ≈ 660 T, or equivalently, the total spin splitting energy 2ΔSO = 2μBHSO ≈ 76 meV. This value agrees well with the values from ab initio calculations for the Fermi surface around the K (K′) point of the Brillouin zone (∼70–80 meV; ref. 19), where the effect of SOIs on Cooper pairing is the strongest. The upper critical field is determined from equation (2) to be Hc20∥ ≈ 35 T, which is more than six times HP. To verify this value, we have performed independent differential conductance measurements of a monolayer at 0.3 K up to H∥ = 31.5 T. (See Supplementary Section 6 for details.) A zero-bias peak originated from Andreev reflections at the normal metal–superconductor contact was observed. With increasing magnetic field, the zero-bias peak diminishes continuously, corresponding to a shrinking superconducting gap, and becomes very weak at 31.5 T (inset of Fig. 4). This result suggests that Hc20∥ ≳ 31.5 T, consistent with the result from equation (2).
. We fit the experimental Hc2∥ − TC dependence to the solution of equation (2) with HSO as a free parameter. The best fit (blue line, Fig. 4) gives the spin–orbit field HSO ≈ 660 T, or equivalently, the total spin splitting energy 2ΔSO = 2μBHSO ≈ 76 meV. This value agrees well with the values from ab initio calculations for the Fermi surface around the K (K′) point of the Brillouin zone (∼70–80 meV; ref. 19), where the effect of SOIs on Cooper pairing is the strongest. The upper critical field is determined from equation (2) to be Hc20∥ ≈ 35 T, which is more than six times HP. To verify this value, we have performed independent differential conductance measurements of a monolayer at 0.3 K up to H∥ = 31.5 T. (See Supplementary Section 6 for details.) A zero-bias peak originated from Andreev reflections at the normal metal–superconductor contact was observed. With increasing magnetic field, the zero-bias peak diminishes continuously, corresponding to a shrinking superconducting gap, and becomes very weak at 31.5 T (inset of Fig. 4). This result suggests that Hc20∥ ≳ 31.5 T, consistent with the result from equation (2).
Finally, we briefly comment on the Hc2∥–TC phase diagram for the few-layer and bulk sample. As N increases, interlayer coupling kicks in, which destroys perfect Ising pairing and introduces orbital effects, both of which decrease the upper critical field Hc20∥. However, for layer thickness much smaller than the out-of-plane penetration depth (∼23 nm; ref. 10), the orbital effect is strongly suppressed20. Similar Hc2∥–TC dependences are observed for few-layer samples with Hc20∥ > 3HP in both bilayer and trilayer NbSe2. The observation of Hc20∥ ≫ HP in few-layer NbSe2 samples suggests a weak coupling between the layers. Indeed, as long as the interlayer-coupling constant (t⊥ ≈ (ℏvF⊥π)/2c ≈ 10 meV, estimated using vF⊥ ≈ 104 ms−1 for the out-of-plane Fermi velocity45 and c ≈ 0.64 nm for the interlayer distance8 in bulk NbSe2) is small compared with the spin splitting energy 2ΔSO ≈ 76 meV, the out-of-plane spin is still approximately a good quantum number. The electron spin, instead of being locked to the momentum, is now locked to each individual layer, which also protects superconductivity under a parallel magnetic field25. Such a spin–layer locking has been observed in related centrosymmetric group-VI TMDs (refs 6,7) and heavy-Fermion superconductor–normal-metal superlattices46. On the other hand, in the bulk limit, the orbital effect dominates the phase diagram as for the case of out-of-plane fields. The estimated in-plane upper critical field Hc20∥ ≈ 17 T (from 70% of the linear extrapolation of the Hc2∥–TC dependence at zero temperature47) is about 4 times higher than Hc20⊥ and is in good agreement with the reported value9,10. We note that the above discussion on the magnetic response of few-layer samples is very qualitative. More detailed experimental and theoretical studies are warranted for a full understanding of the interplay between spin–layer locking and orbital effects, and of the importance of the complex Fermi surface of NbSe2 (refs 13,14). We further note that studies of interplay between SOIs and superconductivity in atomically thin materials may also lead to 2D topological superconductivity48.
Methods
Sample preparation and device fabrication.
High-quality 2H-NbSe2 single crystals were grown from Nb metal wires of 99.95% purity and Se pellets of 99.999% purity by iodine 99.8% vapour transport in a gradient of 730–700 °C in a sealed quartz tube for 21 days. A very slight excess of Se was introduced (typically 0.2% of the charge) to ensure stoichiometry in the resulting crystals. Thin flakes were mechanically exfoliated from bulk single crystals on silicone elastomer polydimethylsiloxane stamps. Atomically thin samples of good geometry were first identified by optical microscopy and then transferred onto silicon substrates (covered by a 280 nm layer of thermal oxide) with pre-patterned Au electrodes. To minimize the environmental effects on the samples, we limited their exposure to air to <1 h. Hexagonal boron nitride (h-BN) thin films of 10–20 nm thickness were introduced as a capping layer for further protection. The sample thickness was determined according to their shear mode frequency by Raman spectroscopy17. The crystal quality was characterized by polarized optical second-harmonic generation. (See Supplementary Section 1 for more details.)
Electrical characterization.
Transport and magnetotransport measurements were carried out in a Physical Property Measurement System down to 2.1 K and up to 9 T. For higher magnetic field measurements up to 31.5 T, a Janis He-3 cryostat with base temperature of 0.3 K was employed. Unless specifically mentioned, longitudinal electrical resistance was acquired using a four-point geometry with excitation current limited to 1 μA to avoid heating and high-bias effects. (Dependence on the excitation current was performed to study the fluctuation effects in two dimensions.) The devices were mounted on a rotation stick, which allows alignment of the sample plane with the external magnetic field with high accuracy (<0.5° error). Multiple devices were prepared and measured. All yielded consistent results for samples of the same thickness.
References
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nature Phys. 10, 343–350 (2014).
Xiao, D., Liu, G.-B., Feng, W., Xu, X. & Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nature Nanotech. 7, 494–498 (2012).
Zeng, H., Dai, J., Yao, W., Xiao, D. & Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nature Nanotech. 7, 490–493 (2012).
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014).
Jones, A. M. et al. Spin-layer locking effects in optical orientation of exciton spin in bilayer WSe2 . Nature Phys. 10, 130–134 (2014).
Riley, J. M. et al. Direct observation of spin-polarized bulk bands in an inversion-symmetric semiconductor. Nature Phys. 10, 835–839 (2014).
Mattheiss, L. F. Band structures of transition-metal-dichalcogenide layer compounds. Phys. Rev. B 8, 3719–3740 (1973).
Foner, S. & McNiff, E. J. Upper critical fields of layered superconducting NbSe2 at low temperature. Phys. Lett. A 45, 429–430 (1973).
de Trey, P., Gygax, S. & Jan, J. P. Anisotropy of Ginzburg–Landau parameter κ in NbSe2 . J. Low Temp. Phys. 11, 421–434 (1973).
Hess, H. F., Robinson, R. B., Dynes, R. C., Valles, J. M. & Waszczak, J. V. Scanning-tunneling-microscope observation of the Abrikosov flux lattice and the density of states near and inside a fluxoid. Phys. Rev. Lett. 62, 214–216 (1989).
Huang, C. L. et al. Experimental evidence for a two-gap structure of superconducting NbSe2: A specific-heat study in external magnetic fields. Phys. Rev. B 76, 212504 (2007).
Yokoya, T. et al. Fermi surface sheet-dependent superconductivity in 2H-NbSe2 . Science 294, 2518–2520 (2001).
Rahn, D. J. et al. Gaps and kinks in the electronic structure of the superconductor 2H-NbSe2 from angle-resolved photoemission at 1 K. Phys. Rev. B 85, 224532 (2012).
Frindt, R. F. Superconductivity in ultrathin NbSe2 layers. Phys. Rev. Lett. 28, 299–301 (1972).
Staley, N. E. et al. Electric field effect on superconductivity in atomically thin flakes of NbSe2 . Phys. Rev. B 80, 184505 (2009).
Xi, X. et al. Strongly enhanced charge-density-wave order in monolayer NbSe2 . Nature Nanotech. 10, 765–769 (2015).
Cao, Y. et al. Quality heterostructures from two-dimensional crystals unstable in air by their assembly in inert atmosphere. Nano Lett. 15, 4914–4921 (2015).
Johannes, M. D., Mazin, I. I. & Howells, C. A. Fermi-surface nesting and the origin of the charge-density wave in NbSe2 . Phys. Rev. B 73, 205102 (2006).
Tinkham, M. Introduction to Superconductivity 2nd edn (McGraw-Hill, 1996).
Chandrasekhar, B. S. A note on the maximum critical field of high-field superconductors. Appl. Phys. Lett. 1, 7–8 (1962).
Clogston, A. M. Upper limit for critical field in hard superconductors. Phys. Rev. Lett. 9, 266–267 (1962).
Bauer, E. & Sigrist, M. Non-centrosymmetric Superconductors: Introduction and Overview (Springer, 2012).
Sigrist, M. Introduction to unconventional superconductivity in non-centrosymmetric metals. AIP Conf. Proc. 1162, 55–97 (2009).
Youn, S. J. et al. Role of strong spin–orbit coupling in the superconductivity of the hexagonal pnictide SrPtAs. Phys. Rev. B 85, 220505(R) (2012).
Fiory, A. T. & Hebard, A. F. Electron mobility, conductivity, and superconductivity near the metal-insulator transition. Phys. Rev. Lett. 52, 2057–2060 (1984).
Beasley, M. R., Mooij, J. E. & Orlando, T. P. Possibility of vortex-antivortex pair dissociation in two-dimensional superconductors. Phys. Rev. Lett. 42, 1165–1168 (1979).
Aslamazov, L. G. & Larkin, A. I. The influence of fluctuation pairing of electrons on conductivity of normal metal. Phys. Lett. A 26, 238–239 (1968).
Li, Q. et al. Interlayer coupling effect in high-Tc superconductors probed by YBa2Cu3O7−x/PrBa2Cu3O7−x superlattices. Phys. Rev. Lett. 64, 3086–3089 (1990).
Schneider, T., Gedik, Z. & Ciraci, S. Transition temperature of superconductor–insulator superlattices. Europhys. Lett. 14, 261–266 (1991).
Prober, D. E., Schwall, R. E. & Beasley, M. R. Upper critical fields and reduced dimensionality of the superconducting layered compounds. Phys. Rev. B 21, 2717–2733 (1980).
Tedrow, P. M. & Meservey, R. Critical magnetic field of very thin superconducting aluminum films. Phys. Rev. B 25, 171–178 (1982).
Lee, I. J., Chaikin, P. M. & Naughton, M. J. Exceeding the Pauli paramagnetic limit in the critical field of (TMTSF)2PF6 . Phys. Rev. B 62, 14669–14672 (2000).
Klemm, R. A. Layered Superconductors Vol. 1 (Oxford Univ. Press, 2012).
Kimura, N. et al. Extremely high upper critical field of the noncentrosymmetric heavy Fermion superconductor CeRhSi3 . Phys. Rev. Lett. 98, 197001 (2007).
Saito, Y. et al. Superconductivity protected by spin-valley locking in gate-tuned MoS2. Preprint at http://arXiv.org/abs/1506.04146 (2015).
Lu, J. M. et al. Two dimensional Ising superconductivity in gated MoS2. Preprint at http://arXiv.org/abs/1506.07620 (2015).
Agosta, C. C. et al. Experimental and semiempirical method to determine the Pauli-limiting field in quasi-two-dimensional superconductors as applied to κ-(BEDT-TTF)2Cu(NCS)2: Strong evidence of a FFLO state. Phys. Rev. B 85, 214514 (2012).
Rainer, D. & Bergmann, G. Temperature dependence of Hc2 and κ1 in strong coupling superconductors. J. Low Temp. Phys. 14, 501–519 (1974).
Orlando, T. P. & Beasley, M. R. Pauli limiting and the possibility of spin fluctuations in the A15 superconductors. Phys. Rev. Lett. 46, 1598–1601 (1981).
Matsuda, Y. & Shimahara, H. Fulde–Ferrell–Larkin–Ovchinnikov state in heavy fermion superconductors. J. Phys. Soc. Jpn 76, 051005 (2007).
Maki, K. Effect of Pauli paramagnetism on magnetic properties of high-field superconductors. Phys. Rev. 148, 362–369 (1966).
Werthamer, N. R., Helfand, E. & Hohenberg, P. C. Temperature and purity dependence of superconducting critical field, Hc2. III. Electron spin and spin–orbit effects. Phys. Rev. 147, 295–302 (1966).
Klemm, R. A., Luther, A. & Beasley, M. R. Theory of upper critical field in layered superconductors. Phys. Rev. B 12, 877–891 (1975).
Kiss, T. et al. Charge-order-maximized momentum-dependent superconductivity. Nature Phys. 3, 720–725 (2007).
Goh, S. K. et al. Anomalous upper critical field in CeCoIn5/YbCoIn5 superlattices with a Rashba-type heavy Fermion interface. Phys. Rev. Lett. 109, 157006 (2012).
Saint-James, D., Sarma, G. & Thomas, E. J. Type II Superconductivity (Pergamon, 1969).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Acknowledgements
We thank M. H. W. Chan for fruitful discussions. This work was supported by the US Department of Energy, Office of Basic Energy Sciences (contract No. DESC0013883 (K.F.M.) and DESC0012635 (J.S.)). Optical spectroscopy was supported by the National Science Foundation (NSF) under Award No. DMR-1410407. The NHMFL is supported by the NSF Cooperative Agreement No. DMR-1157490 and the State of Florida. K.T.L. is supported by HKUST3/CRF/13G and the Croucher Innovation Grant. The work in Lausanne was supported by the Swiss National Science Foundation. We also acknowledge support from the NSF MRSEC under Award No. DMR-1420451 (Z.W.) and the MRI-2D Center at Penn State University (X.X.).
Author information
Authors and Affiliations
Contributions
J.S. and K.F.M. designed the experiments. X.X. and Z.W. performed the experiments with the assistance of W.Z. at the Penn State Physics Low Temperature Laboratory, and of J.-H.P. at the National High Magnetic Field Laboratory. X.X., Z.W., J.S. and K.F.M. analysed the data and co-wrote the paper. K.T.L. contributed to the interpretation of the results. H.B. and L.F. contributed NbSe2 crystals. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 23345 kb)
Rights and permissions
About this article
Cite this article
Xi, X., Wang, Z., Zhao, W. et al. Ising pairing in superconducting NbSe2 atomic layers. Nature Phys 12, 139–143 (2016). https://doi.org/10.1038/nphys3538
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3538
This article is cited by
-
Thickness dependence of superconductivity in layered GeP5
Rare Metals (2024)
-
Superconducting tunnel junctions with layered superconductors
Quantum Frontiers (2024)
-
Atomically Substitutional Engineering of Transition Metal Dichalcogenide Layers for Enhancing Tailored Properties and Superior Applications
Nano-Micro Letters (2024)
-
Interplay between the atomic structures and superconductivity of two-monolayer Pb films
Science China Physics, Mechanics & Astronomy (2024)
-
Superconducting dome by tuning through a van Hove singularity in a two-dimensional metal
npj 2D Materials and Applications (2023)