Abstract
Research on high-temperature superconducting cuprates is at present focused on identifying the relationship between the classic ‘pseudogap’ phenomenon1,2 and the more recently investigated density wave state3,4,5,6,7,8,9,10,11,12,13. This state is generally characterized by a wavevector Q parallel to the planar Cu–O–Cu bonds4,5,6,7,8,9,10,11,12,13 along with a predominantly d-symmetry form factor14,15,16 (dFF-DW). To identify the microscopic mechanism giving rise to this state17,18,19,20,21,22,23,24,25,26,27,28,29, one must identify the momentum-space states contributing to the dFF-DW spectral weight, determine their particle–hole phase relationship about the Fermi energy, establish whether they exhibit a characteristic energy gap, and understand the evolution of all these phenomena throughout the phase diagram. Here we use energy-resolved sublattice visualization14 of electronic structure and reveal that the characteristic energy of the dFF-DW modulations is actually the ‘pseudogap’ energy Δ1. Moreover, we demonstrate that the dFF-DW modulations at E = −Δ1 (filled states) occur with relative phase π compared to those at E = Δ1 (empty states). Finally, we show that the conventionally defined dFF-DW Q corresponds to scattering between the ‘hot frontier’ regions of momentum-space beyond which Bogoliubov quasiparticles cease to exist30,31,32. These data indicate that the cuprate dFF-DW state involves particle–hole interactions focused at the pseudogap energy scale and between the four pairs of ‘hot frontier’ regions in momentum space where the pseudogap opens.
Similar content being viewed by others
Main
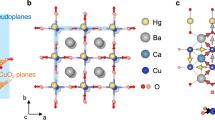
A conventional ‘Peierls’ charge density wave (CDW) in a metal results from particle–hole interactions which open an energy gap at specific regions of k-space that are connected by a common wavevector Q. This generates a modulation in the density of free charge at Q along with an associated modulation of the crystal lattice parameters. Such CDW states are now very well known33. In principle, a density wave modulating at Q can also exhibit a ‘form factor’ (FF) with different possible symmetries34,35 (see Supplementary Section 1). This is relevant to the high-temperature superconducting cuprates because numerous researchers have recently proposed that the ‘pseudogap’ regime1,2 (PG in Fig. 1a) contains an unconventional density wave with a d-symmetry form factor17,18,19,20,21,22,23,24,25,26,27,28,29. The basic phenomenology of such a state is that intra-unit-cell (IUC) symmetry breaking renders the Ox and Oy sites within each CuO2 unit-cell electronically inequivalent, and that this inequivalence is then modulated periodically at wavevector Q parallel to (1,0);(0,1). The real-space (r-space) schematic of such a d-symmetry FF density wave (dFF-DW) at Qx, as shown in Fig. 1b, exemplifies periodic modulations at the Ox sites that are π out of phase with those at the Oy sites. Such a state is then described by A(r) = D(r)cos(φ(r) + φ0(r)), where A(r) represents whatever is the modulating electronic degree of freedom, φ(r) = Qx ⋅ r is the DW spatial phase at location r, φ0(r) represents disorder related spatial phase shifts, and D(r) is the magnitude of the d-symmetry form factor14,21,23. To distinguish between the various microscopic mechanisms proposed for the Q = (Q, 0); (0, Q) dFF-DW state of cuprates17,18,19,20,21,22,23,24,25,26,27,28,29, it is essential to establish its atomic-scale phenomenology, including the momentum space (k-space) eigenstates contributing to its spectral weight, the relationship (if any) between modulations occurring above and below the Fermi energy, whether the modulating states in the DW are associated with a characteristic energy gap, and how the dFF-DW evolves with doping.
a, Schematic phase diagram of hole-doped cuprates. The pseudogap regime has been identified by, for example, suppression of uniform magnetic susceptibility and electronic specific heat, and the appearance of a truncated Fermi surface, referred to as the ‘Fermi arc’1,2. The dome-shaped region of d-symmetry Cooper-paired high-temperature superconductivity is universally accepted. More recently, an unusual density wave state has been detected by bulk probes4,5,6,7,8,9,10,11,12,13 in the region indicated schematically in pink; its modulations are now known to have a d-symmetry form factor14,15,16. The range of hole density, p, in which d-symmetry form factor density waves are studied in this paper is indicated by the white double-headed arrow. b, Schematic of the electronic structure in a cuprate dFF-DW. Grey dots represent the Cu sites and correspond to the white dots in c. The Ox and Oy sites within each CuO2 unit-cell are electronically inequivalent, as represented by a colour scale ranging from yellow through white to blue. The schematic DW modulates horizontally with wavelength λ, or with wavevector Qx (horizontally), and with period 4a0. The periodic modulations at Ox sites are π out of phase with those at Oy sites, as seen by considering the two trajectories marked φx and φy (Supplementary Section 1). c, Measured Z(r, 150 meV) at T > Tc in the pseudogap phase of Bi2Sr2CaCu2O8 at hole density p ∼ 8%. Two periods of dFF-DW modulation at Qx that correspond directly to the schematic in b are shown. Thus, to observe the dFF-DW state, sublattice-phase-resolved imaging is required and achieved here in the pseudogap regime. The transparent overlay shows the relationship between locations of Cu, Ox,Oy atoms in the CuO2 plane and the dFF-DW, whose wavevector here is along the x-direction
To visualize such phenomena directly as in Fig. 1c, we use sublattice-phase-resolved imaging of the electronic structure14 of the CuO2 plane. Both the scanning tunnelling microscope (STM) tip–sample differential tunnelling conductance dI/dV (r, E = eV) ≡ g(r, E) and the tunnel-current I(r, E) are measured at bias voltage V = E/e and with sub-unit-cell spatial resolution. Because the density of electronic states N(r, E) is related to the differential conductance as g(r, E) ∝ [eIs/N(r, E′)dE′]N(r, E), with Is and Vs being arbitrary parameters and the denominator N(r, E′)dE′ unknown, valid imaging of N(r, E) is challenging (Supplementary Section 2). However, one can suppress these serious systematic ‘set-point’ errors by using R(r, E) = I(r, E)/I(r, −E) or Z(r, E) = g(r, E)/g(r, −E); this allows distances, wavelengths and spatial phases of electronic structure to be measured accurately. The unprocessed g(r, E) acquired for and analysed in this paper are measured over very large fields of view (to achieve high phase precision in Fourier analysis), simultaneously maintain deeply sub-unit-cell precision measurements in r (to achieve high precision in sublattice segregation), and are taken over a wide range of energies E with fine energy spacing, so that energy dependences of d-symmetry FF modulations may be accurately determined. We then calculate each sublattice-phase-resolvedZ(r, E) image and separate it into three: the first, Cu(r), contains only the measured values of Z(r) at Cu sites, whereas the other two, Ox(r) and Oy(r), contain only the measurements at the x/y-axis oxygen sites. Phase-resolved Fourier transforms of the Ox(r) and Oy(r) sublattice images14,  ;
;  , are used to determine the form factor symmetry for modulations at any q
, are used to determine the form factor symmetry for modulations at any q



where the superscript Z identifies the type of sublattice-resolved data used. Specifically for a DW occurring at Q, one can then evaluate the magnitude of its d-symmetry form factor  and its s′- and s-symmetry form factors
and its s′- and s-symmetry form factors  and
and  , respectively. Studies of non-energy-resolved R(r, E) images using this approach have revealed that the DW modulations in the Ox(r) and Oy(r) sublattice images of electronic structure in underdoped Bi2Sr2CaCu2O8+x and Ca2−xNaxCuO2Cl2 consistently exhibit a relative phase of π and therefore a predominant d-symmetry form factor14; X-ray scattering studies15,16 yield the same conclusion for two other cuprates, YBa2Cu3O7−x and Bi2Sr2−xLaxCuO6+δ.
, respectively. Studies of non-energy-resolved R(r, E) images using this approach have revealed that the DW modulations in the Ox(r) and Oy(r) sublattice images of electronic structure in underdoped Bi2Sr2CaCu2O8+x and Ca2−xNaxCuO2Cl2 consistently exhibit a relative phase of π and therefore a predominant d-symmetry form factor14; X-ray scattering studies15,16 yield the same conclusion for two other cuprates, YBa2Cu3O7−x and Bi2Sr2−xLaxCuO6+δ.
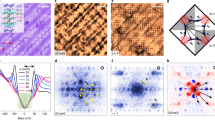
Such X-ray scattering studies now generally report a short-ranged density wave with wavevector centred around Q = (Q, 0); (0, Q) occurring approximately in the pink shaded regions11,12,13 of the schematic phase diagram in Fig. 1a. Figure 1b, c exemplifies the predominately d-symmetry form factor14,15,16 of this DW when imaged directly. One obstacle to understanding this dFF-DW state is that large-field-of-view sublattice-resolved images of cuprate electronic structure14 never look like an ideal long-range ordered version of Fig. 1b. Instead, Fig. 2a shows a typical Z(r, 150 meV) image of p = 8% Bi2Sr2CaCu2O8+x, for T ≪ Tc in the superconducting phase, whereas Fig. 2b shows the equivalent Z(r, 150 meV) for T > Tc in the cuprate pseudogap phase. Although elements indistinguishable from Fig. 1c can be seen in 2a, b, no long-range order is obvious. Therefore, to explore the spatial arrangements of the dFF-DW in such electronic-structure images, we analyse  , which is a robust sublattice-phase-resolved measure of the d-symmetry form factor (Supplementary Section 3). Analysis of Fig. 2a, b in this fashion yields Fig. 2c, d; both clearly exhibit the dFF-DW maxima at the two inequivalent wavevectors Qx and Qy. Fourier filtering these two
, which is a robust sublattice-phase-resolved measure of the d-symmetry form factor (Supplementary Section 3). Analysis of Fig. 2a, b in this fashion yields Fig. 2c, d; both clearly exhibit the dFF-DW maxima at the two inequivalent wavevectors Qx and Qy. Fourier filtering these two  from Fig. 2a, b for only those regions surrounding Qx and Qy (within dashed circles) generates two complex-valued r-space images Dx(r), Dy(r)
from Fig. 2a, b for only those regions surrounding Qx and Qy (within dashed circles) generates two complex-valued r-space images Dx(r), Dy(r)

where Λ−1 is the characteristic length scale over which variations in Dx(r), Dy(r) can be resolved, and is set by the filter width in Fourier space.
a, Measured Z(r, 150 meV) at T ≪ Tc in the superconducting phase of hole density p ∼ 8%-doped Bi2Sr2CaCu2O8+x (T ∼ 4.2 K). These complex spatial features involve modulations that comprehensively maintain a relative phase of π betweenOx and Oy in a disordered d-symmetry FF density wave. b, Measured Z (r, 150 meV) at T > Tc in the pseudogap phase of hole density p ∼ 8%-doped Bi2Sr2CaCu2O8 (T ∼ 45 K). Although correlation lengths are shorter, the dFF-DW phenomena are otherwise indistinguishable from observations at T ≪ Tc. c, The d-symmetry form factor power spectral density  determined from sublattice-phase-resolved analysis of data in a. Two primary DW peaks at Qx and Qy exist with this d-symmetry form factor, as identified by dashed circles. d, The d-symmetry FF power spectral density
determined from sublattice-phase-resolved analysis of data in a. Two primary DW peaks at Qx and Qy exist with this d-symmetry form factor, as identified by dashed circles. d, The d-symmetry FF power spectral density  determined from sublattice-phase-resolved analysis of data in b. Again, two primary DW peaks at Qx and Qy exist with this d-symmetry form factor, showing that the q-space structure of dFF-DW phenomenology is identical in the pseudogap phase and in the superconducting phase. e,f, Using only the regions within the dashed circles in c,d, the r-space amplitudes of the dFF-DW in a,b are calculated for modulations along Qx from (5), and along Qy from (6). Then using F(r) = (|Dx(r)| − |Dy(r)|)/(|Dx(r) +| Dy(r) |) (see Supplementary Section 3) regions primarily modulating along y-axis with −1.0 < F(r) < −0.3 are shaded blue. Regions primarily modulating along x-axis with +0.3 < F(r) < +1.0 are shaded orange. g, Domain configuration of unidirectional dFF-DW modulations contained in Fig. 1a at T ≪ Tc. The unidirectionality colour scale for F(r) demonstrated in e,f is overlaid on the data in a. The dashed circle shows the r-space radius equivalent to the q-space filter used to generate the Dx, y(r) images by Fourier filtering (see Supplementary Section 4). h, Domain configuration of unidirectional dFF-DW modulations contained in Fig. 1b at T > Tc. The unidirectionality colour scale for F(r) demonstrated in e,f is overlaid on the data in b. The dashed circle has same definition as in g.
determined from sublattice-phase-resolved analysis of data in b. Again, two primary DW peaks at Qx and Qy exist with this d-symmetry form factor, showing that the q-space structure of dFF-DW phenomenology is identical in the pseudogap phase and in the superconducting phase. e,f, Using only the regions within the dashed circles in c,d, the r-space amplitudes of the dFF-DW in a,b are calculated for modulations along Qx from (5), and along Qy from (6). Then using F(r) = (|Dx(r)| − |Dy(r)|)/(|Dx(r) +| Dy(r) |) (see Supplementary Section 3) regions primarily modulating along y-axis with −1.0 < F(r) < −0.3 are shaded blue. Regions primarily modulating along x-axis with +0.3 < F(r) < +1.0 are shaded orange. g, Domain configuration of unidirectional dFF-DW modulations contained in Fig. 1a at T ≪ Tc. The unidirectionality colour scale for F(r) demonstrated in e,f is overlaid on the data in a. The dashed circle shows the r-space radius equivalent to the q-space filter used to generate the Dx, y(r) images by Fourier filtering (see Supplementary Section 4). h, Domain configuration of unidirectional dFF-DW modulations contained in Fig. 1b at T > Tc. The unidirectionality colour scale for F(r) demonstrated in e,f is overlaid on the data in b. The dashed circle has same definition as in g.
Their magnitudes


represent the local amplitudes of dFF-DW modulations along Qx and Qy, respectively. Any unidirectional domain arrangements of the dFF-DW state can then be determined by introducing

which is designed to identify regions where the dFF-DW modulation is primarily along the x-axis or the y-axis, depending on the sign of F(r) (Supplementary Section 4). Figure 2e, f shows how regions of −1.0 < F(r) < −0.3 (shaded blue) are primarily modulating along y-axis whereas regions +0.3 < F(r) < +1.0 (shaded orange) are primarily modulating along x-axis (those with −0.3 < F(r) < +0.3 shaded white appear at boundaries). Figure 2g, h reveals the results of this analysis for the data in Fig. 2a, b respectively. Overall, the system is configured into spatial regions within which the dFF-DW along only one direction is dominant. By overlaying the colour scale for F(r) on the data in Fig. 2a, b to create Fig. 2g, h, one can see directly the unidirectional region configurations derived from equation (7). These observations of coexisting nanoscale unidirectional regions are in reasonable agreement with deductions from related X-ray studies36 of YBa2Cu3O7−x. Finally, because the data in Fig. 2b and Fig. 2h were measured at T > Tc (pink region Fig. 1a), this demonstrates directly that the cuprate dFF-DW appears first in the non-superconducting ‘pseudogap’ regime.
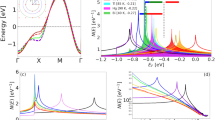
A conventional CDW state opens a gap in the energy spectrum of k-space electronic eigenstates with the maximum spectral weight of modulating states occurring at the edges of this energy gap33. But which energy gap (if any) is associated with the dFF-DW state found in underdoped cuprates is unknown. Figure 3a shows how a typical tunnelling conductance spectrum representative of strongly underdoped cuprates exhibits two characteristic energies30,31,32. Whereas the lower-energy scale Δ0 represents the maximum energy at which Bogoliubov quasiparticle excitations exist30,31,32 (see Fig. 3b), the higher-energy scale (dashed blue line) is the cuprate ‘pseudogap’ as determined from its comparison with the doping dependence of the pseudogap scale in tunnelling and photoemission. To identify the energy dependence of the cuprate dFF-DW states, we measure Z(r, |E|), and from it calculate  ,
,  and
and  . Figure 3c shows the measured power spectral density of the d-symmetry FF modulations
. Figure 3c shows the measured power spectral density of the d-symmetry FF modulations  , with the wavevectors near Qx and Qy indicated by red circles. Adopting the common convention in X-ray studies9,10,11,16 for estimating the DW wavevector magnitude |Q|, we measure
, with the wavevectors near Qx and Qy indicated by red circles. Adopting the common convention in X-ray studies9,10,11,16 for estimating the DW wavevector magnitude |Q|, we measure  along a line in the high-symmetry directions (1,0):(0,1) passing through the region of the dFF-DW peak and fit these data to a background plus Gaussian; the peak positions of the two Gaussians are then assigned to be the values of Qx and Qy. It is important to appreciate, however, that a wide range of Q values can actually be detected under each peak in
along a line in the high-symmetry directions (1,0):(0,1) passing through the region of the dFF-DW peak and fit these data to a background plus Gaussian; the peak positions of the two Gaussians are then assigned to be the values of Qx and Qy. It is important to appreciate, however, that a wide range of Q values can actually be detected under each peak in  and in X-ray scattering intensities; it remains to be determined whether these broad peaks with incommensurate maxima are due to domains of continuously incommensurate dFF-DW or domains of commensurate dFF-DW separated by discommensuration37. Nevertheless, Fig. 3b plots the energy dependence of the dFF-DW wavevectors (blue line) determined in this way for a p = 0.06 sample. Such information was not previously available from measurements of the modulation wavevectors from STM images lacking sublattice-phase-resolved segregation14 into
and in X-ray scattering intensities; it remains to be determined whether these broad peaks with incommensurate maxima are due to domains of continuously incommensurate dFF-DW or domains of commensurate dFF-DW separated by discommensuration37. Nevertheless, Fig. 3b plots the energy dependence of the dFF-DW wavevectors (blue line) determined in this way for a p = 0.06 sample. Such information was not previously available from measurements of the modulation wavevectors from STM images lacking sublattice-phase-resolved segregation14 into  and
and  . Figure 3e shows the measured k-space locus where Bogoliubov quasiparticles exist30,31,32 as a function of hole density. When the dispersive ‘octet’ of Bogoliubov scattering interference disappears, a transition occurs to an ultra-slow dispersing density wave modulation (Fig. 3b). In Fig. 3d, the doping dependence of the conventional Qx, Qy of the d-symmetry form factor modulations is shown using blue symbols, while the shortest wavevectors interconnecting the measured k-space regions where Bogoliubov scattering interference disappears (Fig. 3e) are indicated by using coloured symbols referring to each hole density in Fig. 3e. These data demonstrate directly that the conventionally determined Qx, Qy of the dFF-DW state correspond to the locations in k-space of these arc tips. Finally, in Fig. 3f we show the measured energy dependences of the amplitudes of the s-, s′- and d-form factor modulations, SZ(E), S′Z(E) and DZ(E), determined by integrating over the region of q-space enclosed by solid red circles in Fig. 3c (Supplementary Section 5). The d-symmetry form factor is negligible for modulations in the low-energy range that contains only Bogoliubov quasiparticles (and which we now see is dominated by s′-symmetry form factors), but it rapidly becomes intense at higher energy and reaches maximum at the pseudogap energy scale, which for this sample is Δ1 ∼ 90 meV. This reveals that the characteristic energy of electronic-structure modulations in the cuprate d-symmetry FF density wave is actually the pseudogap energy.
. Figure 3e shows the measured k-space locus where Bogoliubov quasiparticles exist30,31,32 as a function of hole density. When the dispersive ‘octet’ of Bogoliubov scattering interference disappears, a transition occurs to an ultra-slow dispersing density wave modulation (Fig. 3b). In Fig. 3d, the doping dependence of the conventional Qx, Qy of the d-symmetry form factor modulations is shown using blue symbols, while the shortest wavevectors interconnecting the measured k-space regions where Bogoliubov scattering interference disappears (Fig. 3e) are indicated by using coloured symbols referring to each hole density in Fig. 3e. These data demonstrate directly that the conventionally determined Qx, Qy of the dFF-DW state correspond to the locations in k-space of these arc tips. Finally, in Fig. 3f we show the measured energy dependences of the amplitudes of the s-, s′- and d-form factor modulations, SZ(E), S′Z(E) and DZ(E), determined by integrating over the region of q-space enclosed by solid red circles in Fig. 3c (Supplementary Section 5). The d-symmetry form factor is negligible for modulations in the low-energy range that contains only Bogoliubov quasiparticles (and which we now see is dominated by s′-symmetry form factors), but it rapidly becomes intense at higher energy and reaches maximum at the pseudogap energy scale, which for this sample is Δ1 ∼ 90 meV. This reveals that the characteristic energy of electronic-structure modulations in the cuprate d-symmetry FF density wave is actually the pseudogap energy.
a, The tunnelling density of states spectrum g(E = eV) = dI/dV (E) typical of underdoped cuprates shown for the p ∼ 6% samples presented in this paper. The energy Δ0 beyond which Bogoliubov QPI does not exist31,32 and the pseudogap energy Δ1 are indicated. b, The energy dispersion of seven dispersive modulations characteristic of Bogoliubov quasiparticle excitations of a d-wave superconductor (q1…q7) shown as red triangles, except for q1 and q5 which are plotted as red circles. These Bogoliubov quasiparticle interference modulations are all simultaneously observable only below the energy Δ0, as indicated by dashed red line (refs 30,31,32); here we demonstrate that they exhibit a predominantly s’-symmetry form factor, indicated by the red colour. At energies above Δ0, the electronic-structure images evolve quickly to consist of only non-dispersive Qxd and Qyd wavevectors of the d-symmetry form factor DW. We plot the dispersion of these modulations by showing the energy dependence of the maxima in  as blue squares, with the blue bars representing the one σ width of each such peak. The same physical modulations when analysed using
as blue squares, with the blue bars representing the one σ width of each such peak. The same physical modulations when analysed using  appear as the non-dispersive Qxs′ and Qys′ wavevectors shown as red circles, with the red bars representing the one σ width of each such peak. c, Measured
appear as the non-dispersive Qxs′ and Qys′ wavevectors shown as red circles, with the red bars representing the one σ width of each such peak. c, Measured  for samples studied herein. The Qxd and Qyd wavevectors of the d-symmetry form factor DW are indicated by two red circles; the data of relevance for determining the energy/momentum dependence of the dFF-DW modulations is contained within each circle. d, Measured doping dependence of the conventionally defined Qx and Qy of the d-symmetry form factor DW in underdoped Bi2Sr2CaCu2O8+xis shown using blue symbols. The measured doping dependence of the q-vector linking tips of arcs beyond which the signature of Bogoliubov quasiparticles disappears (e and refs 30,31,32) is shown by all other colours. e, Measured doping dependence of the wavevectors interconnecting the k-space arc tips at which Bogoliubov quasiparticle signatures disappear (b and refs 30,31,32). f, Measured energy dependence of S′(E), where q is integrated over the region inside the solid red circles in c, is shown in red. Measured energy dependence of S(E), where q is integrated over the region inside the solid red circles in c, is shown in black. Measured energy dependence of the d-symmetry form factor D(E), where q is integrated over the region inside the solid red circles in c, is shown in blue (Supplementary Section 4). These data reveal that the dFF-DW spectral weight is concentrated at energies surrounding ∼90 meV, which, at this hole density, is the independently measured pseudogap energy scale Δ1 (see a), and is indicated on all relevant panels by a dashed blue line.
for samples studied herein. The Qxd and Qyd wavevectors of the d-symmetry form factor DW are indicated by two red circles; the data of relevance for determining the energy/momentum dependence of the dFF-DW modulations is contained within each circle. d, Measured doping dependence of the conventionally defined Qx and Qy of the d-symmetry form factor DW in underdoped Bi2Sr2CaCu2O8+xis shown using blue symbols. The measured doping dependence of the q-vector linking tips of arcs beyond which the signature of Bogoliubov quasiparticles disappears (e and refs 30,31,32) is shown by all other colours. e, Measured doping dependence of the wavevectors interconnecting the k-space arc tips at which Bogoliubov quasiparticle signatures disappear (b and refs 30,31,32). f, Measured energy dependence of S′(E), where q is integrated over the region inside the solid red circles in c, is shown in red. Measured energy dependence of S(E), where q is integrated over the region inside the solid red circles in c, is shown in black. Measured energy dependence of the d-symmetry form factor D(E), where q is integrated over the region inside the solid red circles in c, is shown in blue (Supplementary Section 4). These data reveal that the dFF-DW spectral weight is concentrated at energies surrounding ∼90 meV, which, at this hole density, is the independently measured pseudogap energy scale Δ1 (see a), and is indicated on all relevant panels by a dashed blue line.
As a function of energy, the transition from Bogoliubov quasiparticle interference (QPI) modulations to dFF-DW modulations occurs in an unusual fashion. Although Bogoliubov QPI is observed as expected everywhere on the Fermi surface in overdoped cuprates32, in underdoped samples it evolves as expected only until the energy E ≈ Δ0, at which the terminations of the Bogoliubov coherent k-space arcs (Fig. 3e) are observed30,31,32. Here, the set of seven dispersive scattering interference modulations q1, q2, …q7 signifying Bogoliubons31 (Supplementary Section 5) disappears in a narrow energy window during which dispersion of the two surviving modulations q1(E) and q5(E) comes to a halt, leaving the ultra-slow dispersing dFF-DW modulations with q1∗ ≈ q1(Δ0) and q5∗ ≈ q5(Δ0) (see Fig. 3b and refs 30,31,32). The intensity of these non-dispersive modulations first becomes detectable at Δ0 and, as we show below, reaches an intense maximum at Δ1, all the while maintaining the same wavevectors Qxd and Qyd, as shown in Fig. 3b. We refer to this k-space region where Bogoliubov quasiparticles yield to modulations of a dFF-DW as the ‘hot frontier’ (we thank S. A. Kivelson for proposing the term ‘hot frontier’ to describe the k-space phenomenology of the cuprate dFF-DW as observed using spectroscopic imaging STM) to distinguish it from the colloquial ‘hot spots’ beyond which, in a conventional density wave, dispersive quasiparticle states would reappear. In cuprates, this does not occur and, instead, the ‘hot frontiers’ define the k-space limit beyond which only dFF-DW modulations are detected30,31,32 using spectroscopic imaging STM (blue in Fig. 3b).
Key information on the microscopic cause of any DW state is also contained in the relationship between modulations of states above and below the Fermi energy. For example, mixing via interactions of states with momenta k1 and k2 generates modulations at wavevector Q = k1–k2. The wavefunctions of any resulting DW would then form bonding/anti-bonding states below/above the Fermi level which are proportional to ± . The related densities of these states would then exhibit modulations governed by | ± = 2(1 ± cos(Q ⋅ r)). In such scenarios, the DW modulations above the Fermi energy should always be π out of phase with the equivalent ones below. To explore this issue in Bi2Sr2CaCu2O8+x, we show in Fig. 4a, b the measured g(r, +94 meV) from filled states and g(r, −94 meV) from empty states, respectively, each at the characteristic energy of the dFF-DW (Fig. 3f and Supplementary Section 6); avoidance of the set-point error is discussed in Supplementary Section 6. For these two images the sublattice-phase-resolved  equation (1) are calculated and reveal a predominantly d-symmetry form factor modulation with wavevectors near Qx and Qy in Fig. 4a, b. Next, by Fourier filtering these two
equation (1) are calculated and reveal a predominantly d-symmetry form factor modulation with wavevectors near Qx and Qy in Fig. 4a, b. Next, by Fourier filtering these two  for regions surrounding Qy, we determine the complex-valued Dy(r), and thus the spatial phase of dFF-DW modulation along Qy as
for regions surrounding Qy, we determine the complex-valued Dy(r), and thus the spatial phase of dFF-DW modulation along Qy as

a, Differential tunnelling conductance image g(r, +94 meV) measured above EF near the pseudogap energy +Δ1. The colour scale is reversed compared to b. b, Differential tunnelling conductance image g(r, −94 meV) measured below EF near the pseudogap energy −Δ1. The colour scale is reversed compared to a. c, The spatial phase of the dFF-DW modulating along the y-direction φy(r, E) is calculated using equation (8) from g(r, +94 meV) data in a. The dashed circle shows the r-space radius equivalent to the q-space filter used to generate the φx, y(r, E) images by Fourier filtering (see Supplementary Section 6). d, The spatial phase of the dFF-DW modulating along the y-direction φy(r, E) is calculated using equation (9) from g(r, −94 meV) data in b. e,f, From the field of view of a and b, we show the energy dependence of the relative phase of g(r, −E) and g(r, +E) modulations along the y-axis (Supplementary Section 5): φy(r, +E) − φy(r, −E) when averaged over every pair of identical pixel locations r (e); similarly for relative phase of g(r, −E) and g(r, +E) for modulations along the x-axis: φx(r, +E) − φx(r, −E) (f). The low-energy modulations at +E and −E are in phase spatially and so have a relative phase difference of 0. As the pseudogap energy Δ1 is approached and the dFF-DW phenomena emerge, the relative spatial phase of empty state and filled state dFF-DW modulations varies wildly in the narrow energy grange shaded grey, and the quickly develops a robust phase shift of π.
This is shown for E = +94 meV in Fig. 4c and for E = −94 meV in Fig. 4d. Visual comparison reveals that these two φy(r, ±E) images are out of phase with each other by π. And, indeed, the spatial-average value of φy(r, +E) − φy(r, −E) as a function of E (over the whole field of view of A and B) is shown in Fig. 4e. It reveals that, whereas the relevant Qx and Qy components of g(r, +E) and g(r, −E) images are in phase with each other at low energy, they rapidly evolve at |E| > 70 meV and become globally π out of phase at |E| ∼ Δ1 (Fig. 4a, b). The shaded region indicates evolution through a situation where some areas exhibit φ ∼ 0 and some φ ∼ π, but this is quickly resolved on reaching the pseudogap energy Δ1. Similar analysis for the particle–hole symmetry in phases φx(r, ± E) of Qx modulations

yields a virtually identical result (Fig. 4f). These phenomena also occur throughout the underdoped regions of the phase diagram (Supplementary Section 6.III), demonstrating that, in the cuprate dFF-DW state, a phase difference of π exists between spatial modulations of the filled states below energy E ∼ −Δ1 and the empty states above E ∼ +Δ1.
To summarize: by introducing techniques to determine the energy/momentum and doping dependence of modulation form factor symmetry, we find that the predominantly d-symmetry form factor density wave exists throughout the underdoped region of the Bi2Sr2CaCu2O8 phase diagram (Fig. 3d), including in the pseudogap regime T > Tc (Figs 1c and 2b). The spatial arrangements are primarily in the form of nanoscale regions, each containing a primarily unidirectional dFF-DW (Fig. 2g, h). The conventionally defined wavevectors Qx and Qy of the dFF-DW state evolve with doping as determined by the four shortest scattering vectors linking the k-space regions beyond which Bogoliubov quasiparticle excitations are non-existent (Fig. 3d, e) and at which the pseudogap emerges. Further, we demonstrate that, as determined in terms of tunnelling probabilities, the dFF-DW state is particle–hole antisymmetric, in the sense that a phase difference of π exists between spatial modulations of the filled states (E ∼ −Δ1) and the empty states (E ∼ +Δ1) (Fig. 4e, f). Perhaps most significantly, we show that the characteristic energy of the cuprate dFF-DW state is actually the pseudogap energy Δ1 (Fig. 3f).
These data provide clear evidence that the cuprate d-symmetry form factor density wave state involves particle–hole interactions, and that these occur primarily very near wavevectors interconnecting the ‘hot frontiers’ in k-space at which the pseudogap emerges30,31,32. Moreover, the dFF-DW electronic-structure modulations have a characteristic energy scale which is the pseudogap energy. This intimate connection of the dFF-DW state with the pseudogap electronic structure is consistent with the fact that this state is found only within the pseudogap regime11,12,13. Of course, electron–lattice interactions can also play a significant role, with the coupling to the B1g modes long being of foremost interest19,20,38. Strong interactions of this mode with the electrons39 ultimately leading to static, finite-Q lattice distortions with d-symmetry form factor15 have recently been discovered in association with the cuprate dFF-DW state. Nevertheless, electron–lattice interactions are not by themselves sufficient to explain the phase diagram of the dFF-DW (refs 11,12,13) because, for example, they also exist in the overdoped regime where the dFF-DW is absent. Moreover, theoretical models involving k-space instabilities26,27,29,40 which are consistent with the results herein, emphasize that a density wave with this Q and form factor symmetry cannot emerge from a large Fermi surface; instead, a pre-existing reorganization of k-space due to the pseudogap would be required. Overall, our data support a microscopic picture in which the exotic electronic structure of the pseudogap is parent to the dFF-DW state and not vice versa, where the energy scale and wavevectors of the dFF-DW are intimately linked to those of the pseudogap, and in which the d-symmetry DW competes directly for spectral weight with the d-symmetry superconductor at the k-space ‘hot frontier’ between superconductivity and the pseudogap.
References
Orenstein, J. & Millis, A. J. Advances in the physics of high-temperature superconductivity. Science 288, 468–474 (2000).
Norman, M. R., Pines, D. & Kallin, C. The pseudogap: Friend or foe of high Tc? Adv. Phys. 54, 715–733 (2005).
Wu, T. et al. Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3Oy. Nature 477, 191–194 (2011).
Chang, J. et al. Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67 . Nature Phys. 8, 871–876 (2012).
Ghiringhelli, G. et al. Long-range incommensurate charge fluctuations in (Y, Nd)Ba2Cu3O6+x . Science 337, 821–825 (2012).
Achkar, A. J. et al. Distinct charge orders in the planes and chains of ortho-III-ordered YBa2Cu3O6+δ superconductors identified by resonant elastic X-ray scattering. Phys. Rev. Lett. 109, 167001 (2012).
Torchinsky, D. H., Mahmood, F., Bollinger, A. T., Božović, I. & Gedik, N. Fluctuating charge-density waves in a cuprate superconductor. Nature Mater. 12, 387–391 (2013).
Blackburn, E. et al. X-ray diffraction observations of a charge-density-wave order in superconducting ortho-II YBa2Cu3O6.54 single crystals in zero magnetic field. Phys. Rev. Lett. 110, 137004 (2013).
Comin, R. et al. Charge order driven by Fermi-arc instability in Bi2Sr2−xLaxCuO6+δ . Science 343, 390–392 (2014).
da Silva Neto, E. H. et al. Ubiquitous interplay between charge ordering and high-temperature superconductivity in cuprates. Science 343, 393–396 (2014).
Blanco-Canosa, S. et al. Resonant X-ray scattering study of charge-density wave correlations in YBa2Cu3O6+x . Phys. Rev. B 90, 054513 (2014).
Hücker, M. et al. Competing charge, spin, and superconducting orders in underdoped YBa2Cu3Oy . Phys. Rev. B 90, 054514 (2014).
Blackburn, E. X-ray diffraction studies of charge density waves in cuprate superconductors: A brief review. Physica B 460, 132–135 (2014).
Fujita, K. et al. Direct phase-sensitive identification of a d-form factor density wave in underdoped cuprates. Proc. Natl Acad. Sci. USA 111, E3026–E3032 (2014).
Forgan, E. M. et al. The nature of the charge density waves in under-doped YBa2Cu3O6.54 revealed by X-ray measurements of the ionic displacements. Preprint at http://arXiv.org/abs/1504.01585 (2015).
Comin, R. et al. The symmetry of charge order in cuprates. Nature Mater. 14, 796–800 (2015).
Li, J.-X., Wu, C.-Q. & Lee, D.-H. Checkerboard charge density wave and pseudogap of high-Tc cuprate. Phys. Rev. B 74, 184515 (2006).
Seo, K., Chen, H.-D. & Hu, J. d-wave checkerboard order in cuprates. Phys. Rev. B 76, 020511 (2007).
Fu, H. C., Honerkampand, C. & Lee, D.-H. Renormalization group study of the electron–phonon interaction in high-Tc cuprates. Europhys. Lett. 75, 146–152 (2006).
Newns, D. M. & Tsuei, C. C. Fluctuating Cu–O–Cu bond model of high-temperature superconductivity. Nature Phys. 3, 184–191 (2007).
Sachdev, S. & La Placa, R. Bond order in two-dimensional metals with antiferromagnetic exchange interactions. Phys. Rev. Lett. 111, 027202 (2013).
Davis, J. C. & Lee, D.-H. Concepts relating magnetic interactions, intertwined electronic orders, and strongly correlated superconductivity. Proc. Natl Acad. Sci. USA 110, 17623–17630 (2013).
Allais, A., Bauer, J. & Sachdev, S. Density wave instabilities in a correlated two-dimensional metal. Phys. Rev. B 90, 155114 (2014).
Fischer, M. H., Wu, S., Lawler, M., Paramekanti, A. & Kim, E.-A. Nematic and spin-charge orders driven by hole-doping a charge-transfer insulator. New J. Phys. 16, 093057 (2014).
Pépin, C., de Carvahlo, V. S., Kloss, T. & Montiel, X. Coexistence of pseudo-gap and charge order at the hot spots in cuprate superconductors. Phys. Rev. B 90, 195207 (2014).
Chowdhury, D. & Sachdev, S. Density wave instabilities of fractionalized Fermi liquids. Phys. Rev. B 90, 245136 (2014).
Atkinson, W. A., Kampf, A. & Bulut, S. Charge order in the pseudogap phase of cuprate superconductors. New J. Phys. 17, 013025 (2015).
Yamakawa, Y. & Kontani, H. Spin-fluctuation-driven nematic charge-density-wave in cuprate superconductors: Charge-orbital-spin multimode fluctuations caused by vertex corrections. Phys. Rev. Lett. 114, 257001 (2015).
Zhang, L. & Mei, J.-W. Reconstructed Fermi surface and quantum oscillation of doped resonating valence bond state with incommensurate charge order in underdoped cuprates. Preprint at http://arXiv.org/abs/1408.6592 (2014).
Kohsaka, Y. et al. How Cooper pairs vanish approaching the Mott insulator in Bi2Sr2CaCu2O8+δ . Nature 454, 1072–1078 (2008).
Fujita, K. et al. Spectroscopic imaging scanning tunneling microscopy studies of electronic structure in the superconducting and pseudogap phases of cuprate high-Tc superconductors. J. Phys. Soc. Jpn 81, 011005 (2011).
Fujita, K. et al. Simultaneous transitions in cuprate momentum-space topology and electronic symmetry breaking. Science 344, 612–616 (2014).
Grüner, G. Density Waves in Solids 31–70 (Westview Press, 1994).
Nayak, C. Density-wave states of nonzero angular momentum. Phys. Rev. B 62, 4880–4889 (2000).
Metlitski, M. A. & Sachdev, S. Quantum phase transitions of metals in two spatial dimensions. I. Ising-nematic order. Phys. Rev. B 82, 075127 (2010).
Comin, R. et al. Broken translational and rotational symmetry via charge stripe order in underdoped YBa2Cu3O6+y . Science 347, 1335–1339 (2015).
Burk, B. et al. Charge-density-wave domains in 1 T-TaS2 observed by satellite structure in scanning-tunneling-microscopy images. Phys. Rev. Lett. 66, 3040–3043 (1991).
Mishra, V. & Norman, M. A strong-coupling critique of spin fluctuation driven charge order in undoped cuprates. Phys. Rev. B 92, 060507(R) (2015).
Le Tacon, M. et al. Inelastic X-ray scattering in YBa2Cu3O6.6 reveals giant phonon anomalies and elastic central peak due to charge-density-wave formation. Nature Phys. 10, 52–58 (2014).
Kloss, T. et al. SU(2) symmetry in a realistic spin-fermion model for cuprate superconductors. Phys. Rev. B 91, 205124 (2015).
Acknowledgements
We acknowledge and thank H. Alloul, D. Chowdhury, R. Comin, A. Damascelli, E. Fradkin, D. Hawthorn, S. Hayden, J. E. Hoffman, M.-H. Julien, D. H. Lee, M. Norman and C. Pepin for helpful discussions and communications. We are especially grateful to S. A. Kivelson for key scientific discussions and advice. Experimental studies were supported by the Center for Emergent Superconductivity, an Energy Frontier Research Center, headquartered at Brookhaven National Laboratory and funded by the US Department of Energy under DE-2009-BNL-PM015, as well as by a Grant-in-Aid for Scientific Research from the Ministry of Science and Education (Japan) and the Global Centers of Excellence Program for Japan Society for the Promotion of Science. C.K.K. acknowledges support under the FlucTeam Program at Brookhaven National Laboratory (Contract DE-AC02-98CH10886). S.D.E., J.C.D. and A.P.M. acknowledge the support of EPSRC through the Programme Grant ‘Topological Protection and Non-Equilibrium States in Correlated Electron Systems’. Theoretical studies at Cornell University were supported by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Science and Engineering under Award DE-SC0010313. Theoretical studies at Harvard University were supported by NSF Grant DMR-1103860 and by the Templeton Foundation. Research at Perimeter Institute is supported by the Government of Canada through Industry Canada and by the Province of Ontario through the Ministry of Research and Innovation. The data and/or materials supporting this publication can be accessed at http://dx.doi.org/10.17630/f17227bc-3045-40d6-b289-30a4c1a8966c.
Author information
Authors and Affiliations
Contributions
M.H.H., S.D.E., C.K.K. and K.F. carried out the experiments; K.F., H.E. and S.U. synthesized and characterized the samples; M.H.H., S.D.E. and K.F. developed and carried out analysis; E.-A.K., M.J.L. and S.S. provided theoretical guidance; A.P.M. and J.C.D. supervised the project and wrote the paper with key contributions from M.H.H., S.D.E., C.K.K. and K.F. The manuscript reflects the contributions and ideas of all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 7770 kb)
Rights and permissions
About this article
Cite this article
Hamidian, M., Edkins, S., Kim, C. et al. Atomic-scale electronic structure of the cuprate d-symmetry form factor density wave state. Nature Phys 12, 150–156 (2016). https://doi.org/10.1038/nphys3519
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3519
This article is cited by
-
Electronic stripe patterns near the fermi level of tetragonal Fe(Se,S)
npj Quantum Materials (2023)
-
Low-energy gap emerging from confined nematic states in extremely underdoped cuprate superconductors
npj Quantum Materials (2023)
-
Dynamic electron correlations with charge order wavelength along all directions in the copper oxide plane
Nature Communications (2021)
-
Atomically-resolved interlayer charge ordering and its interplay with superconductivity in YBa2Cu3O6.81
Nature Communications (2021)
-
Dictionary learning in Fourier-transform scanning tunneling spectroscopy
Nature Communications (2020)