Abstract
The Carnot cycle imposes a fundamental upper limit to the efficiency of a macroscopic motor operating between two thermal baths1. However, this bound needs to be reinterpreted at microscopic scales, where molecular bio-motors2 and some artificial micro-engines3,4,5 operate. As described by stochastic thermodynamics6,7, energy transfers in microscopic systems are random and thermal fluctuations induce transient decreases of entropy, allowing for possible violations of the Carnot limit8. Here we report an experimental realization of a Carnot engine with a single optically trapped Brownian particle as the working substance. We present an exhaustive study of the energetics of the engine and analyse the fluctuations of the finite-time efficiency, showing that the Carnot bound can be surpassed for a small number of non-equilibrium cycles. As its macroscopic counterpart, the energetics of our Carnot device exhibits basic properties that one would expect to observe in any microscopic energy transducer operating with baths at different temperatures9,10,11. Our results characterize the sources of irreversibility in the engine and the statistical properties of the efficiency—an insight that could inspire new strategies in the design of efficient nano-motors.
Similar content being viewed by others
Main
The Carnot cycle consists of two isothermal processes, where the working substance is respectively in contact with thermal baths at different temperatures Th and Tc, connected by two adiabatic processes, where the substance is isolated and heat is not delivered nor absorbed. An external parameter is changed in such a way that the whole cycle is carried out reversibly. Following this scheme, one could devise a progressing miniaturization of a Carnot engine and eventually reproduce the cycle with a single Brownian particle. In fact, a variety of thermodynamic processes and even a complete Stirling cycle have been already implemented in the mesoscale using micro-manipulation techniques3,4,5,12,13,14. Interestingly, the exchange of energy between the particle and its surrounding environment becomes stochastic at the microscale and yet one can rigorously define work, heat and efficiency, within the framework of the recently developed stochastic thermodynamics6,7.
The experimental realization of a Carnot cycle with a single Brownian particle has remained elusive owing to the difficulties of implementing an adiabatic process. In particular, it is not clear how to isolate a particle from the surrounding fluid15. A more feasible strategy is to simultaneously change the temperature and the external parameter keeping constant the Shannon entropy of the particle. However, the necessary fine-tuning of the temperature is an experimental challenge as well. Here we construct a Brownian Carnot engine putting forward an experimental technique that allows precise control of both the effective temperature and the accessible volume of a single microscopic particle (see Methods and refs 16,17,18). We use a particle with an inherent electric charge and apply a noisy electrostatic force that mimics a thermal bath. In this way, we can achieve temperatures ranging from room temperature (no electrostatic force) up to hundreds or even thousands of kelvins, far above the boiling point of water.
The working substance of our engine is a single optically trapped colloidal particle immersed in water14. For small displacements x from the trap equilibrium position, the optical potential is harmonic, U(x, t) = κx(t)2/2, with stiffness κ. The Hamiltonian or total energy of the particle is H = κx2/2 + p2/(2m), with p = m(dx/dt) being the linear momentum of the particle and m the mass of the particle. The conjugated force for the external parameter κ is Fκ(t) ≡ ∂H/∂κ = x2(t)/2. As a result, the work necessary to implement a change dκ in the external parameter, dW(t) = Fκ(t)dκ, and the heat or energy transfer from the thermal bath to the particle, dQ(t) = dH(t) − dW(t), are fluctuating quantities.
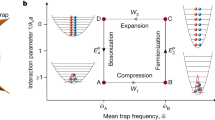
The Carnot cycle is implemented by modifying the stiffness κ and the environment temperature T (Fig. 1a, b) and consists of two isothermal processes (T is kept constant and κ changes, blue and red curves in Fig. 1b) and two adiabatic processes (T and κ change keeping T2/κ constant14, green and magenta curves in Fig. 1b). We measure different thermodynamic quantities (temperature, stiffness, heat, work and Shannon entropy, see Methods) under both equilibrium and non-equilibrium driving (Fig. 1b–d). The effective temperature of the particle is obtained from the average potential energy, Tpart(t) ≡ κ(t)〈x(t)2〉/k, and can differ from the environment temperature T for non-quasistatic protocols. The Tpart − κ diagram of the engine (Fig. 1b) shows larger fluctuations in the quasistatic equilibrium protocol, because the average is taken over a smaller number of cycles. In the non-equilibrium protocol, the most irreversible steps are the expansions, where the particle remains colder (that is, more confined19) than the environment. As in a macroscopic gas, the expansion is dominated by an entropic force, namely, the tendency of the gas to fill the available space. In the case of the single Brownian particle, the expansion is driven by thermal fluctuations that allow the particle to move farther away from the centre of the trap. On the other hand, the compression is driven by the trap confining force, which allows the particle to react more rapidly and to follow the equilibrium temperature even in fast cycles in the adiabatic compression. In the isothermal compression, however, we observe a fast initial increase of the temperature of the particle due to the increase of the stiffness. The Fκ − κ diagram (Fig. 1c) resembles the Clapeyron pressure versus volume diagram of a Carnot cycle performed with an ideal gas20. The Tpart − S diagram of the particle (Fig. 1d) is a rectangle where all of the entropy changes in the system occur in the two isothermal steps. This diagram also gives information about the nature of the irreversibility for a fast driving (open symbols): the effective temperature of the particle in the isothermal processes suggests the presence of an irreversible flow of energy between the reservoir and the particle, resembling the endo-reversible engine introduced by Curzon and Ahlborn21,22. During a cycle of duration τ, the working substance of the engine exchanges heat with the different thermal baths it is put in contact with, and under appropriate conditions it is able to extract work. We call Wτ and Qτ the work exerted on the particle and the heat transferred from the environment to the particle along a cycle, respectively. The exchanged heat equals Qτ = ΔHτ − Wτ. Both work and heat along the whole cycle (Fig. 2a) converge to their quasistatic averages 〈 ⋅ ∞〉 following 〈Wτ〉 = 〈W∞〉 + Σss/τ (ref. 23). Here, 〈W∞〉 is the quasistatic value of the work done per cycle and the term Σss/τ accounts for the (positive) dissipation, which decays to zero like 1/τ (ref. 24). In the case of the average heat per cycle, 〈Qτ〉, we find that the dissipative term is negative, that is, 〈Qτ〉 = 〈Q∞〉 − Σss/τ with Σss > 0.
a, Time evolution of the experimental protocol. b–d, Thermodynamic diagrams of the engine: (1) isothermal compression (blue); (2) adiabatic compression (magenta); (3) isothermal expansion (red); (4) adiabatic expansion (green). Solid lines are the analytical values in the quasistatic limit. Filled symbols are obtained from ensemble averages over cycles of duration τ = 200 ms; open symbols are obtained for τ = 30 ms. The black arrow indicates the direction of the operation of the engine. b, Tpart − κ diagram. c, Clapeyron diagram. The area within the cycle is equal to the mean work obtained during the cycle. d, Tpart–S diagram. The entropy changes only in the isothermal steps.
a, Ensemble averages of stochastic work (〈Wτ〉, blue stars) and heat (〈Qτ〉, red pluses) transferred in one cycle as a function of the cycle duration. Green crosses are the average total energy change of the working substance 〈ΔHτ〉. Thin lines are fits to A + B/τ. b, Power output Pτ = −〈Wτ〉/τ (black diamonds, left axis) and long-term efficiency ητ (yellow hexagons, right axis) as a function of the inverse of the cycle time. The black curve is a fit Pτ = (〈W∞〉 + Σss/τ)/τ, yielding 〈W∞〉 = (−0.38 ± 0.01)kTc and Σss = (5.7 ± 0.3)kTc ms with a reduced chi-square of χred2 = 1.08. The solid yellow line is a fit to ητ = (ηC + τW/τ)/(1 + τQ/τ), which yields η∞ = (0.92 ± 0.06)ηC,τW = (−11 ± 2) ms,τQ = (−0.6 ± 6.0) ms with χred2 = 0.76. Yellow dash–dot line is the Curzon–Ahlborn efficiency  , which is in excellent agreement with the location of the maximum power (vertical black dashed line). Ensemble averages are done over 50 s and error bars are obtained with a statistical significance of 90%.
, which is in excellent agreement with the location of the maximum power (vertical black dashed line). Ensemble averages are done over 50 s and error bars are obtained with a statistical significance of 90%.
To quantify the performance of the engine, we analyse its power output and efficiency. First, we measure the power output as the mean total work exchanged during a cycle divided by the total duration of the cycle (Fig. 2b), Pτ = −〈Wτ〉/τ. For τ = 10 ms, 〈Wτ〉 is positive, the particle behaves as a heat pump and the power is negative. For larger values of τ the power increases, becoming positive, and eventually reaches a maximum value Pmax = 6.34 kTc s−1. Above that maximum, Pτ decreases monotonically when increasing the cycle length. The data of Pτ versus τ fit well to the expected law Pτ = −(〈W∞〉 + Σss/τ)/τ. The efficiency is given by the ratio between the extracted work and the input of heat, which is usually considered as the heat flowing from the hot thermal bath to the system. In our experiment, however, there is a non-zero fluctuating heat in the adiabatic steps, which must be taken into account in the definition of the stochastic efficiency of the engine during a finite number of cycles. Here we will consider this heat as input (see Methods for alternative definitions of the efficiency). We define Wτ(i) as the sum of the total work exerted on the particle along i ≥ 1 cycles of duration τ, and Qα, τ(i) as the sum over i cycles of the heat transferred to the particle in the αth subprocess (α = 1,2,3,4, see Fig. 1). We therefore introduce the following definition of stochastic efficiency:

The long-term efficiency of the motor is given by ητ ≡ ητ(i) with i → ∞. In the quasistatic limit, the average heat in the adiabatic processes vanishes yielding η∞ = ηC ≡ 1 − Tc/Th ≃ 0.43 (Fig. 2b). Moreover, the standard efficiency at maximum power, η∗ ≃ (0.25 ± 0.05), is in agreement with the Curzon–Ahlborn expression for finite-time cycles  (refs 21,25).
(refs 21,25).
Very recently, much attention has been drawn to the statistical properties of the efficiency of stochastic engines. Using fluctuation theorems, it was shown that the probability density function (PDF) of the efficiency of an autonomous or symmetrically driven engine has a local minimum precisely at the Carnot value ηC (ref. 26). For non-symmetric driving protocols, such as our Carnot cycle, there are several theoretical predictions concerning the PDF as well as the large deviation function of the stochastic efficiency10,11. To test some of these predictions, we measure the PDF ρτ, i(η) of the stochastic efficiency ητ(i) (Methods). Close to equilibrium, near the maximum power output of the engine, the distribution is bimodal when summing over several cycles9,11 (Fig. 3). Indeed, local maxima of ρτ, i(η) appear above standard efficiency for large values of i. Another universal feature tested here is that the tails of the distribution follow a power law, ρτ, i(η → ± ∞) ∼ η−2 (inset of Fig. 3)11,27. In the Supplementary Information, we discuss in detail and provide further experimental tests of other universal properties of the PDF and the large deviation function of the stochastic efficiency. We have realized the first Brownian Carnot engine with a single microscopic particle as a working substance that is able to transform the heat transferred from thermal fluctuations into mechanical work, characterizing both its mean behaviour and fluctuations. At slow driving, our engine attains the fundamental limit of Carnot efficiency. The maximum power performed by our engine is ∼250 larger than that of previous micro-engines3 and only one order of magnitude below the power developed by some biological molecular motors such as myosin2. Our results could be exploited in the design of new biologically inspired nano-engines28 or artificial nanorobots29. In vacuum, trapping techniques could benefit from our study of the efficiency fluctuations to build engines capable of outperforming Carnot efficiency30,31,32.
Contour plot of the PDF of the efficiency ρτ=40 ms, i(η) computed summing over i = 1 to400 cycles (left axis). The long-term efficiency (averaged over τexp = 50 s) is shown with a vertical blue dashed line. Super Carnot efficiencies appear even far from quasistatic driving. Inset: tails of the distribution for ρτ=40 ms, 10(η) (blue pluses, positive tail; red stars, negative tail). The green line is a fit to a power law to all the data shown, whose exponent is γ = (−1.9 ± 0.3).
Methods
Experimental set-up.
Polystyrene microspheres of diameter 1 μm (G. Kisker-Products for Biotechnology) are diluted in deionized and filtered water to a final concentration of a few spheres per millilitre. The spheres are inserted into a custom-made electrophoretic fluid chamber with two electrodes. A Gaussian white noise signal is generated with an independent generator (Tabor electronics, WW1071). The external noise is modulated by a custom-made voltage multiplier (100 kHz bandwidth) with a signal (VT) generated by a dual generator (Tabor electronics, dual channel WW5062). The output signal of the multiplier is amplified 1,000 times with a high-voltage power amplifier (TREK, 623B) before being applied to the electrodes.
The optical potential is generated by a 980 nm laser beam which is inserted through an oil immersion objective (Nikon, CFI PL FL × 100 NA 1.30) into the fluid chamber. The detection of the motion of the particle is achieved by an additional 532 nm laser beam that is passed through the trapping objective. The forward scattered light is collected by an additional microscope objective (×10, NA = 0.10), and its back focal-plane field distribution is analysed by a quadrant position detector (New Focus 2911) at an acquisition rate of 2 kHz. A laser controller (Arroyo Instruments 4210) allows the management of the optical power at a maximum rate of 250 kHz using an external voltage Vκ. The trap stiffness depends linearly on the optical power and can be controlled at the same rate as it. The signal sent to the laser controller (Vκ) is also generated by the dual generator, and is hence synchronized with VT.
Experimental protocol.
The electronic control of the protocol allows us to implement it at different cycle times without loss of resolution, ranging from τ = 10 ms to τ = 200 ms, during τexp = 50 s. For simplicity, we impose a time-symmetric protocol for the stiffness, {κ(t)}t=0τ with κ(t) = κ(τ − t). The stiffness increases quadratically with time from t = 0 to t = τ/2 and decreases at the same rate from τ/2 to τ. We fix the minimum and maximum values of the stiffness, κI = κ(0) = (2.0 ± 0.2) pN μm−1 and κIII = κ(τ/2) = (20.0 ± 0.2) pN μm−1 respectively. For convenience, we define κII = κ(τ/4) = (6.5 ± 0.2) pN μm−1. The geometry of the Carnot cycle imposes the value of κIV = (κIII/κII)κI = κ(τ∗) = (6.2 ± 0.2) pN μm−1, where τ∗ yields  . The temperature of the particle remains constant at the isothermal steps: TI = TII = Tc = 300 K during t ∈ [0, τ/2] and TIII = TIV = Th = 525 K during t ∈ [τ/2, τ∗]. Along the adiabatic steps, the temperature changes smoothly while T2(t)/κ(t) remains constant to ensure that the total Shannon entropy of the system is conserved14,33.
. The temperature of the particle remains constant at the isothermal steps: TI = TII = Tc = 300 K during t ∈ [0, τ/2] and TIII = TIV = Th = 525 K during t ∈ [τ/2, τ∗]. Along the adiabatic steps, the temperature changes smoothly while T2(t)/κ(t) remains constant to ensure that the total Shannon entropy of the system is conserved14,33.
Data analysis.
For each cycle of duration τ, we sample the position of the bead with respect to the centre along the x axis set by the direction of the external field. In all cases, we measure trajectories of the position {xt}t=0τ with sampling rate 2 kHz (Δt = 5 ms) along τexp = 50 s. The stochastic work exerted to the particle in the interval of time [t, t + Δt] in a single realization is given by


where ° denotes the Stratonovich product (ref. 6) and Fκ(xt, t) = ∂U(xt, t)/∂κt = xt2/2 is the generalized force conjugated to the control parameter κ. The stochastic heat transferred in [t, t + Δt] from the effective thermal bath to the particle is calculated using the first law of thermodynamics:

where dUt = (1/2)(κt+Δtxt+Δt2 − κtxt2) is the change in potential energy, dEkin, t = (m/2)(vt+Δt2 − vt2) is the kinetic energy change, and dWt is given by equation (2). Equation (3) equals Sekimoto’s celebrated expression for microscopic heat6. Both work and heat along the elementary processes in the cycle are calculated by summing the contributions of equations (2) and (3) from the beginning to the end of the process. The kinetic energy of the particle (of mass m and friction coefficient γ) at time t, vt, is calculated from the time-averaged velocity at time t,  :
:

where  is a correction factor that depends on the acquisition frequency f = 1/Δt and on the physical parameters of the system at time t:
is a correction factor that depends on the acquisition frequency f = 1/Δt and on the physical parameters of the system at time t:

where fp = γ/m, fκ = κt/2πγ,  and
and  (refs 13,14).
(refs 13,14).
The Shannon entropy of the particle at time t, St, is measured as the sum of the positional and kinetic entropy, St = Sx, t + Sv, t. Here, Sx, t = −k∫ dxt ρ(xt, t)lnρ(xt, t), where ρ(xt, t) is the PDF to observe trajectories that pass through xt at time t along the experiment. The distribution ρ(xt, t) is estimated from the histogram of xt using a regular binning of 25 bins in the interval [−3σ(xt), 3σ(xt)], with σ(xt) being the standard deviation of the position at time t. The same procedure is applied to determine Sv, t = −k∫ dvt ρ(vt, t)lnρ(vt, t), binning in the interval [−3σ(vt), 3σ(vt)] in this case, with vt being determined using equations (4) and (5).
For a given cycle of duration τ, we first calculate the distribution of ητ(i) for i = [1,2,3, …, 400] cycles. For each value of i, the PDFρ(η(i)) is estimated as follows: we first compute the values of ητ(i) (equation (1) in the main text) along the experiment as the ratio of the work summed over i consecutive cycles over the heat summed over the same i cycles. This procedure is repeated along all of the cycles of the experiment. The distributions shown in Fig. 3 are calculated using a kernel density routine in MATLAB R2013a by partitioning the data in regular bins ranging from −5ηC to 5ηC of width 0.02ηC. The tails of the distribution (inset of Fig. 3) are sampled using a binning of width 0.4ηC.
Efficiency fluctuations in the quasistatic limit.
The traditional definition of efficiency for a heat engine operating between two thermal baths is the ratio between work extracted in the cycle and heat absorbed during the hot isothermal,

If heat is exchanged during other steps different from isothermals, even if only because of fluctuations, it may be relevant to reflect this in the efficiency. Thus, these two other definitions for the efficiency are possible:

For example, ητ2, (i) is the type of efficiency usually considered when the heat in step 2 (the step just before the hot isothermal expansion) is exchanged with the hot bath, as in the microscopic Stirling motor3 (with step 2 corresponding to the isochoric heating in this case).
The corresponding long-term efficiencies are obtained with the limits i → ∞ and τ → ∞:

where W∞ = limi→∞(W∞(i)/i), and the same for the heat. Theoretically, these three definitions of long-term efficiency converge to Carnot efficiency, as heat exchanges in the adiabatic steps vanish on average. However, the experimental long-term efficiencies do not coincide for large τ (data not shown). Carnot efficiency is approached best by η3 in the quasistatic limit. This can be understood by noting that η3 is the quantity with the smallest fluctuations around ηC of the three in this limit. Thus, when averaging over a finite number of cycles this approaches Carnot efficiency faster.
We can analyse the fluctuations of η3 in the quasistatic limit by noting that the work is delta distributed. Then, the denominator in η3 can be expressed using the first law applied to the process 2 → 3 → 4, as

where W is the total work in the cycle and W1 is work in the cold isothermal, both deterministic quantities. Here I and II refer to the initial and final state of the system during the subprocess 1. This yields

where HII–HI is the total energy difference between the initial and final state in the cold isothermal and is the only fluctuating quantity in the expression. The quasistatic averages of the work in the cold isothermal and in the cycle are equal to

and then

The distribution of the internal energy change is given by

with βc = 1/kTc. From this, we can compute the variance of HI − HII, which reads

This gives a variance for η3 of

and for the relative fluctuation

Equivalently, the variance of η1 in the quasistatic limit reads

Fluctuations on η1 are a factor Th/Tc stronger than those of η3 and values for η1 computed from averages of a small finite number of cycles will in general be less reliable than those of η3. When considering the intermediate case of η2, the variance can be shown to be equal to

Our theoretical results predict that the width of the long-term efficiencies satisfy Δη3 ≲ Δη2 ≪ Δη1, which indicates than when estimating efficiencies η3 is expected to have the least experimental error associated with fluctuations.
References
Carnot, S. Annales scientifiques de l’École Normale Supérieure Vol. 1, 393–457 (Société mathématique de France, 1872).
Howard, J. Mechanics of Motor Proteins and The Cytoskeleton (Sinauer Associates Sunderland, 2001).
Blickle, V. & Bechinger, C. Realization of a micrometre-sized stochastic heat engine. Nature Phys. 8, 143–146 (2012).
Roldán, E., Martínez, I. A., Parrondo, J. M. R. & Petrov, D. Universal features in the energetics of symmetry breaking. Nature Phys. 10, 457–461 (2014).
Koski, J. V., Maisi, V. F., Pekola, J. P. & Averin, D. V. Experimental realization of a szilard engine with a single electron. Proc. Natl Acad. Sci. USA 111, 13786–13789 (2014).
Sekimoto, K. Lecture Notes in Physics Vol. 799 (Springer Verlag, 2010).
Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 75, 126001 (2012).
Wang, G. M., Sevick, E. M., Mittag, E., Searles, D. J. & Evans, D. J. Experimental demonstration of violations of the second law of thermodynamics for small systems and short time scales. Phys. Rev. Lett. 89, 050601 (2002).
Polettini, M., Verley, G. & Esposito, M. Efficiency statistics at all times: Carnot limit at finite power. Phys. Rev. Lett. 114, 050601 (2015).
Verley, G., Willaert, T., Van den Broeck, C. & Esposito, M. Universal theory of efficiency fluctuations. Phys. Rev. E 90, 052145 (2014).
Gingrich, T. R., Rotskoff, G. M., Vaikuntanathan, S. & Geissler, P. L. Efficiency and large deviations in time-asymmetric stochastic heat engines. New J. Phys. 16, 102003 (2014).
Toyabe, S., Sagawa, T., Ueda, M., Muneyuki, E. & Sano, M. Experimental demonstration of information-to-energy conversion and validation of the generalized jarzynski equality. Nature Phys. 6, 988–992 (2010).
Roldán, E., Martínez, I. A., Dinis, L. & Rica, R. A. Measuring kinetic energy changes in the mesoscale with low acquisition rates. Appl. Phys. Lett. 104, 234103 (2014).
Martínez, I. A., Roldán, É, Dinis, L., Petrov, D. & Rica, R. A. Adiabatic processes realized with a trapped Brownian particle. Phys. Rev. Lett. 114, 120601 (2015).
Crooks, G. E. & Jarzynski, C. Work distribution for the adiabatic compression of a dilute and interacting classical gas. Phys. Rev. E 75, 021116 (2007).
Martínez, I. A., Roldán, É, Parrondo, J. M. R. & Petrov, D. Effective heating to several thousand kelvins of an optically trapped sphere in a liquid. Phys. Rev. E 87, 032159 (2013).
Mestres, P., Martinez, I. A., Ortiz-Ambriz, A., Rica, R. A. & Roldan, E. Realization of nonequilibrium thermodynamic processes using external colored noise. Phys. Rev. E 90, 032116 (2014).
Bérut, A., Petrosyan, A. & Ciliberto, S. Energy flow between two hydrodynamically coupled particles kept at different effective temperatures. Europhys. Lett. 107, 60004 (2014).
Gieseler, J., Deutsch, B., Quidant, R. & Novotny, L. Subkelvin parametric feedback cooling of a laser-trapped nanoparticle. Phys. Rev. Lett. 109, 103603 (2012).
Feynman, R., Leighton, R. & Sands, M. The Feynman Lectures on Physics 2nd edn, Vol. 1 (Addison-Wesley, 1963).
Curzon, F. & Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 43, 22–24 (1975).
Ouerdane, H., Apertet, Y., Goupil, C. & Lecoeur, P. Continuity and boundary conditions in thermodynamics: From Carnot’s efficiency to efficiencies at maximum power. Eur. Phys. J. Spec. Top. 224, 839–864 (2015).
Sekimoto, K. & Sasa, S.-i. Complementarity relation for irreversible process derived from stochastic energetics. J. Phys. Soc. Jpn 66, 3326–3328 (1997).
Bonanca, M. V. S. & Deffner, S. Optimal driving of isothermal processes close to equilibrium. J. Chem. Phys. 140, 244119 (2014).
Esposito, M., Kawai, R., Lindenberg, K. & Van den Broeck, C. Efficiency at maximum power of low-dissipation Carnot engines. Phys. Rev. Lett. 105, 150603 (2010).
Verley, G., Esposito, M., Willaert, T. & den Broeck, C. V. The unlikely Carnot efficiency. Nature Commun. 5, 5721 (2014).
Proesmans, K., Cleuren, B. & Van den Broeck, C. Stochastic efficiency for effusion as a thermal engine. Europhys. Lett. 109, 20004 (2015).
Sarikaya, M., Tamerler, C., Jen, A. K.-Y., Schulten, K. & Baneyx, F. Molecular biomimetics: Nanotechnology through biology. Nature Mater. 2, 577–585 (2003).
Douglas, S. M., Bachelet, I. & Church, G. M. A logic-gated nanorobot for targeted transport of molecular payloads. Science 335, 831–834 (2012).
Roßnagel, J., Abah, O., Schmidt-Kaler, F., Singer, K. & Lutz, E. Nanoscale heat engine beyond the Carnot limit. Phys. Rev. Lett. 112, 030602 (2014).
Gieseler, J., Quidant, R., Dellago, C. & Novotny, L. Dynamic relaxation of a levitated nanoparticle from a non-equilibrium steady state. Nature Nanotech. 9, 358–364 (2014).
Millen, J., Deesuwan, T., Barker, P. & Anders, J. Nanoscale temperature measurements using non-equilibrium Brownian dynamics of a levitated nanosphere. Nature Nanotech. 9, 425–429 (2014).
Sekimoto, K., Takagi, F. & Hondou, T. Carnot’s cycle for small systems: Irreversibility and cost of operations. Phys. Rev. E 62, 7759–7768 (2000).
Acknowledgements
I.A.M., É.R., D.P. and R.A.R. acknowledge financial support from Fundació Privada Cellex Barcelona. I.A.M., D.P. and R.A.R. acknowledge financial support from grant NanoMQ (FIS2011-24409, MINECO). I.A.M. acknowledges financial support from the European Research Council Grant OUTEFLUCOP. É.R., L.D. and J.M.R.P. acknowledge financial support from grant ENFASIS (FIS2011-22644, MINECO) and TerMic (FIS2014-52486-R, MINECO). We wish to acknowledge the work of S. Corcuff at the earliest stage of the project and fruitful discussions with R. Brito. D. Petrov passed away on 3 February 2014. He initiated the development of this project while he was the leader of the Optical Tweezers group at ICFO. We mourn the loss of a great colleague and friend.
Author information
Authors and Affiliations
Contributions
I.A.M. designed the experiment, obtained all experimental data and analysed experimental data. É.R. designed the experiment, analysed experimental data and supported theoretical aspects. L.D. supported theoretical aspects. D.P. proposed and established the project, and supervised the experiment. J.M.R.P. proposed and established the project and developed its theoretical aspects. R.A.R. supported and supervised the experiment. All authors discussed the results and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 617 kb)
Rights and permissions
About this article
Cite this article
Martínez, I., Roldán, É., Dinis, L. et al. Brownian Carnot engine. Nature Phys 12, 67–70 (2016). https://doi.org/10.1038/nphys3518
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3518
This article is cited by
-
Heating and cooling are fundamentally asymmetric and evolve along distinct pathways
Nature Physics (2024)
-
Overcoming power-efficiency tradeoff in a micro heat engine by engineered system-bath interactions
Nature Communications (2023)
-
Introduction to quantum thermodynamic cycles
Journal of Chemical Sciences (2023)
-
One-particle engine with a porous piston
Scientific Reports (2022)
-
Tunable Brownian magneto heat pump
Scientific Reports (2022)