Abstract
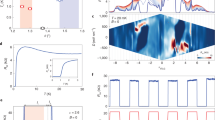
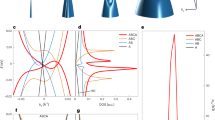
A class of multilayered functional materials has recently emerged in which the component atomic layers are held together by weak van der Waals forces that preserve the structural integrity and physical properties of each layer. An exemplar of such a structure is a transistor device in which relativistic Dirac fermions can resonantly tunnel through a boron nitride barrier, a few atomic layers thick, sandwiched between two graphene electrodes. An applied magnetic field quantizes graphene’s gapless conduction and valence band states into discrete Landau levels, allowing us to resolve individual inter-Landau-level transitions and thereby demonstrate that the energy, momentum and chiral properties of the electrons are conserved in the tunnelling process. We also demonstrate that the change in the semiclassical cyclotron trajectories, following an inter-layer tunnelling event, is analogous to the case of intra-layer Klein tunnelling.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
References
Liu, Y., Bian, G., Miller, T. & Chiang, T.-C. Visualizing electronic chirality and Berry phases in graphene systems using photoemission with circularly polarized light. Phys. Rev. Lett. 107, 166803 (2011).
Katsnelson, M. I., Novoselov, K. S. & Geim, A. K. Chiral tunnelling and the Klein paradox in graphene. Nature Phys. 2, 620–625 (2006).
Young, A. F. & Kim, P. Quantum interference and Klein tunnelling in graphene heterojunctions. Nature Phys. 5, 222–226 (2009).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Britnell, L. et al. Field-effect tunneling transistor based on vertical graphene heterostructures. Science 335, 947–950 (2012).
Mishchenko, A. et al. Twist-controlled resonant tunnelling in graphene/boron nitride/graphene heterostructures. Nature Nanotech. 9, 808–813 (2014).
Fallahazad, B. et al. Gate-tunable resonant tunneling in double bilayer graphene heterostructures. Nano Lett. 15, 428–433 (2015).
Britnell, L. et al. Resonant tunnelling and negative differential conductance in graphene transistors. Nature Commun. 4, 1794 (2013).
Feenstra, R. M., Jena, D. & Gu, G. Single-particle tunneling in doped graphene–insulator–graphene junctions. J. Appl. Phys. 111, 043711 (2012).
Zhao, P., Feenstra, R. M., Gu, G. & Jena, D. SymFET: A proposed symmetric graphene tunneling field-effect transistor. IEEE Trans. Electron Devices 60, 951–957 (2013).
Brey, L. Coherent tunneling and negative differential conductivity in a graphene/h-BN/graphene heterostructure. Phys. Rev. Appl. 2, 014003 (2014).
Vasko, F. T. Resonant and nondissipative tunneling in independently contacted graphene structures. Phys. Rev. B 87, 075424 (2013).
Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Coulomb barrier to tunneling between parallel two-dimensional electron systems. Phys. Rev. Lett. 69, 3804 (1992).
Leadbeater, M. L., Sheard, F. W. & Eaves, L. Inter-Landau-level transitions of resonantly tunnelling electrons in tilted magnetic fields. Semicond. Sci. Technol. 6, 1021–1024 (1991).
Lee, G. H. et al. Electron tunneling through atomically flat and ultrathin hexagonal boron nitride. Appl. Phys. Lett. 99, 243114 (2011).
Lopes dos Santos, J. M. B., Peres, N. M. R. & Castro Neto, A. H. Graphene bilayer with a twist: Electronic structure. Phys. Rev. Lett. 99, 256802 (2007).
Mele, E. J. Commensuration and interlayer coherence in twisted bilayer graphene. Phys. Rev. B 81, 161405 (2010).
Bistritzer, R. & MacDonald, A. H. Transport between twisted graphene layers. Phys. Rev. B 81, 245412 (2010).
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 122337 (2011).
Shon, N. & Ando, T. Quantum transport in two-dimensional graphite system. J. Phys. Soc. Jpn 67, 2421–2429 (1998).
Zheng, Y. & Ando, T. Hall conductivity of a two-dimensional graphite system. Phys. Rev. B 65, 245420 (2002).
Zhang, Y., Tan, Y. W., Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 438, 201–204 (2005).
Li, G., Luican, A. & Andrei, E. Y. Scanning tunneling spectroscopy of graphene on graphite. Phys. Rev. Lett. 102, 176804 (2009).
Fu, Y.-S. et al. Imaging the two-component nature of Dirac–Landau levels in the topological surface state of Bi2Se3 . Nature Phys. 10, 815–819 (2014).
Miller, D. L. et al. Real-space mapping of magnetically quantized graphene states. Nature Phys. 6, 811–817 (2010).
Zhang, Y. et al. Landau-level splitting in graphene in high magnetic fields. Phys. Rev. Lett. 96, 136806 (2006).
Li, G., Luican-Mayer, A., Abanin, D., Levitov, L. & Andrei, E. Y. Evolution of Landau levels into edge states in graphene. Nature Commun. 4, 1744 (2013).
Luican-Mayer, A. et al. Screening charged impurities and lifting the orbital degeneracy in graphene by populating Landau levels. Phys. Rev. Lett. 112, 036804 (2013).
Ponomarenko, L. A. et al. Density of states and zero Landau level probed through capacitance of graphene. Phys. Rev. Lett. 105, 136801 (2010).
Pratley, L. & Zülicke, U. Magnetotunneling spectroscopy of chiral two-dimensional electron systems. Phys. Rev. B 88, 245412 (2013).
Pratley, L. & Zülicke, U. Valley filter from magneto-tunneling between single and bi-layer graphene. Appl. Phys. Lett. 104, 082401 (2014).
Pershoguba, S. S., Abergel, D. S. L., Yakovenko, V. M. & Balatsky, A. V. Effects of a tilted magnetic field in a Dirac double layer. Phys. Rev. B 91, 085418 (2015).
Acknowledgements
This work was supported by the EU Graphene Flagship Programme and ERC Synergy Grant, Hetero2D. M.T.G. acknowledges The Leverhulme Trust for support of an Early Career Fellowship. V.I.F. acknowledges support of a Royal Society Wolfson Research Merit Award. E.E.V. and S.V.M. were supported by NUST ”MISiS” (grant K1-2015-046) and RFBR (15-02-01221 and 14-02-00792).
Author information
Authors and Affiliations
Contributions
Y.C. and A.V.K., fabricated the devices. E.E.V., A.M., O.M., A.P., K.S.N., A.V.K., M.J.Z. and L.E., designed and/or carried out the experiments. M.T.G., T.M.F., L.E., E.E.V., A.M., S.V.M., J.R.W., V.I.F., K.S.N. and A.K.G., undertook the interpretation of the data. M.T.G. performed the calculations. M.T.G., T.M.F. and L.E. wrote the manuscript with contributions from the other authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 2438 kb)
Supplementary Movie
Supplementary Movie 1 (AVI 4890 kb)
Rights and permissions
About this article
Cite this article
Greenaway, M., Vdovin, E., Mishchenko, A. et al. Resonant tunnelling between the chiral Landau states of twisted graphene lattices. Nature Phys 11, 1057–1062 (2015). https://doi.org/10.1038/nphys3507
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3507
This article is cited by
-
A magnetically-induced Coulomb gap in graphene due to electron-electron interactions
Communications Physics (2023)
-
Time, momentum, and energy resolved pump-probe tunneling spectroscopy of two-dimensional electron systems
Nature Communications (2023)
-
Gate- versus defect-induced voltage drop and negative differential resistance in vertical graphene heterostructures
npj Computational Materials (2022)
-
Observation of interaction-induced phenomena of relativistic quantum mechanics
Communications Physics (2021)
-
Topologically distinct Weyl fermion pairs
Scientific Reports (2021)