Thermodynamic signature of a magnetic-field-driven phase transition within the superconducting state of an underdoped cuprate

Abstract

More than a quarter century after the discovery of the high-temperature superconductor (HTS) YBa₂Cu₃O_6+δ (YBCO; ref. 1), studies continue to uncover complexity in its phase diagram. In addition to HTS and the pseudogap^2,3, there is growing evidence for multiple phases with boundaries which are functions of temperature (T), doping (p) and magnetic field^4,5,6,7,8. Here we report the low-temperature electronic specific heat (C_elec) of YBa₂Cu₃O_6.43 and YBa₂Cu₃O_6.47 (p = 0.076 and 0.084) up to a magnetic field (H) of 34.5 T, a poorly understood region of the underdoped H–T–p phase space. We observe two regimes in the low-temperature limit: below a characteristic magnetic field H′ ≈ 12–15 T, C_elec/T obeys an expected H^1/2 behaviour^9,10; however, near H′ there is a sharp inflection followed by a linear-in-H behaviour. H′ rests deep within the superconducting phase and, thus, the linear-in-H behaviour is observed in the zero-resistance regime¹¹. In the limit of zero temperature, C_elec/T is proportional to the zero-energy electronic density of states. At one of our dopings, the inflection is sharp only at lowest temperatures, and we thus conclude that this inflection is evidence of a magnetic-field-driven quantum phase transition.

Main

In elemental metals, the total low-temperature specific heat has the well-known form C = γT + βT³—a sum of a linear term due to the electrons (C_elec) and a cubic term due to the phonons. For ideal, perfectly clean $d_{x^2-y^2}$ superconductors, this form must be modified to C(H = 0, T) = αT² + βT³ owing to the linear electronic density of states that arises from the presence of symmetry-enforced nodal lines along which the momentum-dependent superconducting gap, Δ_k, vanishes linearly with slope dΔ_k/dk = v_Δ (ref. 12). Experimental measurements of the low-temperature specific heat of HTS cuprates in magnetic fields applied along the c-axis have found that C_elec(H, T) = γ(H)T (refs 13,14), consistent with theoretically predicted scaling for d-wave quasiparticles experiencing an ‘orbital’ Doppler shift from superconducting vortices: γ(H) − γ(H = 0) ∼ H^1/2/v_Δ (ref. 9).

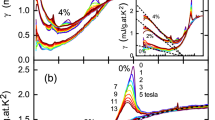
We have measured the specific heat of samples of YBa₂Cu₃O_6.47 (abbreviated according to the convention YBCO6.47) with T_c = 49 K and YBCO6.43 with T_c = 41 K, corresponding to hole dopings p = 0.084 and 0.076, respectively¹⁵. The total specific heat (C) for H < H′ strongly resembles previously reported results for YBCO6.56 (ref. 16). That is, for YBCO6.47, between 1 K and 8 K, we find C_elec(H < H′)/T = γ(H = 0) + A_cH^1/2, with H′ = 12 T, γ(H = 0) = 2.1 mJ mol⁻¹ K⁻² (Fig. 1) and A_c = 0.6 mJ mol⁻¹ K⁻² T^−1/2 (Fig. 2). The phonon term, β = 0.38 mJ mol⁻¹ K⁻⁴, varies negligibly (< 1%) over the full range of H (Fig. 1). Our second doping, YBCO6.43, also approximately follows C_elec(H < H′)/T = γ(H = 0) + A_cH^1/2 below 3 K, with H′ = 12 T, γ(H = 0) = 2.5 mJ mol⁻¹ K⁻² (Fig. 1) and A_c = 0.6 mJ mol⁻¹ K⁻² T^−1/2 (Fig. 2). The data from YBCO6.43 in Figs 1d and 2b have a greater dependence on temperature than the data for YBCO6.47 in Figs 1b and 2a, yet they still follow the more general scaling law for d-wave superconductivity (ref. 10) below H′ ≈ 15 T (Fig. 3). For both YBCO6.43 and YBCO6.47, the values of A_c are within experimental error of the value measured for YBCO6.56 of A_c = 0.57 mJ mol⁻¹ K⁻² T^−1/2 (ref. 16; see Supplementary Table 1 and Supplementary Fig. 8). At a further intermediate doping of p = 0.097, YBCO6.51, we have measured similar samples up to 15 T and also find γ(H = 0) = 2.3 mJ mol⁻¹ K⁻² and A_c = 0.64 mJ mol⁻¹ K⁻² T^−1/2 (see Supplementary Table 1 and Supplementary Figs 9 and 10). We infer from these A_c values that v_Δ ≈ 0.15–0.17 eV Å (refs 17,18) and is insensitive to doping, despite the fact that the onset of finite resistance occurs at a magnetic field (H_R) that is a factor of ∼1.5 higher in YBCO6.43 and YBCO6.47 than YBCO6.56 at low temperatures¹¹ (see Supplementary Information). The value of v_Δ in YBCO for p = 0.08–0.10 is strikingly similar to two other materials at the same dopings: in Bi₂Sr₂CaCu₂O_8+δ (BSCCO), as shown by scanning tunnelling microscopy (STM; ref. 19) and angle-resolved photoemission spectroscopy (ARPES) (v_Δ ≈ 0.11–0.12 eV Å; ref. 20), as well as values of A_c from the specific heat of La_2−xSr_xCuO₄ (ref. 21), from which we determine v_Δ ≈ 0.16 eV Å (refs 17,18). This constant magnitude of v_Δ for underdoped YBCO, with T_c ranging from 41 K to 59 K, which is similar to two other cuprates with T_c varying from 20 K (underdoped LSCO; refs 17,18) to 92 K (near-optimum-doped BSCCO; ref. 20), strongly implies that the pairing scale (inferred from v_Δ) does not determine T_c for underdoped cuprates. v_Δ is relatively constant over the range of dopings recently studied by means of the specific heat (p = 0.075–0.1, see Supplementary Table 1) and yet roughly a factor of two larger than v_Δ measured at optimal doping, despite T_c in the latter being greater than 90 K. That is, the energy gap is larger even though T_c is lower in the underdoped samples studied here.

Figure 1: Temperature dependence of the specific heat.

a, Total C/T versusT² for YBCO6.47 at H = 0 T (black) and 34.5 T (blue) with linear fits (red) to determine γ(H = 0) = 2.2 mJ mol⁻¹ K⁻², β(H = 0) = 0.381 mJ mol⁻¹ K⁻⁴ and β(H = 34.5 T) = 0.382 mJ mol⁻¹ K⁻⁴. b, ΔC_elec/T versus T for YBCO6.47 at various fields. c, As in a, but for YBCO6.43, giving γ(H = 0) = 2.5 mJ mol⁻¹ K⁻², β(H = 0) = 0.407 mJ mol⁻¹ K⁻⁴ and β(H = 34.5 T) = 0.411 mJ mol⁻¹ K⁻⁴. d, As in b, but for YBCO6.43. Error bars in plots are ± one standard deviation for a single data collection (see Supplementary Methods). The arrows in b indicate the approximate position of the resistive transition for H ≥ 29 T as reported for YBCO6.47 (ref. 11).

Figure 2: Field dependence of electronic specific heat.

a, ΔC_elec/T versus H for YBCO6.47. The dashed black curve and line are guides to the eye, given by ΔC_elec/T = 0.6 mJ mol⁻¹ K⁻² T^−1/2 × H^1/2 and ΔC_elec/T = 0.17 mJ mol⁻¹ K⁻² T⁻¹ × H, respectively, where H is given in tesla. b, ΔC_elec/T versus H for YBCO6.43. Again, the dashed curve and line are guides to the eye: ΔC_elec/T = 0.6 mJ mol⁻¹ K⁻² T^−1/2 × H^1/2 and ΔC_elec/T = 0.155 mJ mol⁻¹ K⁻² T⁻¹ × H, respectively. Error bars in plots are ± one standard deviation for a single data collection (see Supplementary Methods).

Figure 3: Scaling plot.

Data from Fig. 1d plus the 2.5 K data from Fig. 2b (red circles) plotted to test for SL scaling for d-wave superconductivity (ref. 10). The data collapse within error for T ≤ 7 K, provided H ≤ 15 T. The dashed black curve traces an approximate scaling function. The legend lists fixed-field curves that follow scaling below ≈7 K. The dotted vertical line indicates an anomaly consisting of a maximum at T/H^1/2 ≈ 1 K T^−1/2 at all fields. The red arrow indicates the upturn in the 2.5 K data. Error bars in plots are ± one standard deviation for a data collection.

We now note that the predicted H = 0 superconducting term C ∼ αT² is not clearly evident; however, we can conclude α < 0.2 mJ mol⁻¹ K⁻³ (see Supplementary Methods). We note further that other specific heat^13,14 and ARPES (ref. 22) measurements are consistent with this upper bound, given that α = 18ζ(3)k_B³n_lab(1/πℏ²v_Fv_Δ) (ref. 12), where v_F is the Fermi velocity, ζ(x) is the Riemann zeta function, ab is the area of the a–b plane per unit cell, and n_l = 2 is the number of CuO₂ layers per mole (see Supplementary Information).

The most striking feature uncovered by the present study is the obvious deviation from ΔC_elec = C_elec(H, T) − C_elec(H = 0, T) ∼ H^1/2 (see Supplementary Methods) characterized by a low-temperature inflection point and subsequent ΔC_elec ∼ H behaviour, as seen in Fig. 2. This approximately linear-in-H behaviour, unprecedented for HTS cuprates, leads to ΔC_elec(H = 34.5 T)/T ≈ 5–6 mJ mol⁻¹ K⁻² (Fig. 1b), roughly twice the value observed in YBCO6.56 at any H ≤ 45 T (ref. 16). Two key facts are evident: (1) a larger specific heat exists at the lower dopings, YBCO6.43 and YBCO6.47, than at the higher doping, YBCO6.56. This is perhaps counterintuitive because superconductivity is more robust at the lower dopings, thus one might expect a larger superconducting gap, which would ordinarily lead to a lower specific heat. That is, at T ≈ 1 K, H_R ≈ 45 T for YBCO6.43 and YBCO6.47, whereas H_R < 35 T for YBCO6.56 (refs 11,16; see Supplementary Information). (2) In YBCO6.56, over any portion of the magnetic field range measured, all evidence points to the absence of linear-in-H enhancement of C_elec above the fit extrapolated from low-field data¹⁶. Moreover, ΔC_elec/T is essentially independent of temperature in YBCO6.47, even for data crossing into the resistive regime at H_R(T), indicated by the arrows in Fig. 1b (ref. 11). The magnetic field dependence of ΔC_elec/T is also not affected by H_R(T). These facts, taken together, make it unlikely that H′ and H_R(T) mark the mean-field suppression of the superconducting gap by a magnetic field. In addition, the abruptness of the change at H′ is at odds with the smoothness expected in the magnetic field suppression of the order parameter of a d-wave superconductor²³.

In Fig. 3, we re-plot the YBCO6.43 data to test for a more general d-wave scaling (SL scaling) predicted by Simon and Lee¹⁰. All data below H′ = 15 T scale within the scatter between 1 and 7 K. The breakdown in scaling above 15 T is most clearly visible in the marked upturn in the 2.5 K trace (Fig. 3), which represents a sharp deviation from scaling. Note that all data for H ≥ 18 T are above H′, and do not scale. A broad maximum centred near 1 K T^−1/2 exists for all fields. The quotient T/H^1/2 is proportional to the ratio of the orbital magnetic length over the thermal length, suggesting the maximum may arise from superconducting vortices: in fact, a similar anomaly in the low-temperature C_elec of d-wave superconductors has been predicted as a consequence of magnetic sub-bands resulting from the periodicity of the vortex lattice²⁴. We re-plot the ∼2 K data of Fig. 2a in Fig. 4a to demonstrate the breakdown of orbital scaling at H′, and to clearly illustrate the sharpness of the transition between the two regimes. The plot depicts a scenario in which the orbital effect, ΔC_elec(H)/T ∝ H^1/2/v_Δ, is responsible for the observed ΔC_elec(H)/T over the entire magnetic field range. Such a scenario would necessitate a field-dependent v_Δ^eff(H) ∝ TH^1/2/ΔC_elec(H) (where v_Δ^eff is an effective field-dependent parameter such that, for H → 0, v_Δ^eff = v_Δ) that is more or less a piecewise function: v_Δ^eff is largely independent of field below H′, followed by a sudden drop at H′ that asymptotes to v_Δ^eff ∝ 1/H^1/2 (Fig. 4a). As v_Δ^eff is proportional to the magnitude of the superconducting order parameter, this further disfavours a mean-field scenario involving suppression of the gap by H (ref. 23).

Figure 4: Calculated effective electronic velocity parameters.

a, Re-plotting of the data in Fig. 2a as v_Δ^eff versusH, (v_Δ ∝ TH^1/2/ΔC_elec for ideal d-wave superconductors with constant v_F^eff). The colour scheme is the same as in Fig. 2a, and dashed lines are again defined by ΔC_elec/T = 0.17 mJ mol⁻¹ K⁻² T⁻¹ × H and ΔC_elec/T = 0.6 mJ mol⁻¹ K⁻² T^−1/2 × H^1/2. Error bars represent ± one standard deviation for one data collection, recalculated for the quantity TH^1/2/ΔC_elec. b, Alternative scenario assuming fixed v_Δ, showing calculated v_F^eff (ref. 18) with both orbital and Zeeman effects included. The value of v_F^eff belowH′ is determined from the thermal conductivity³⁰. The drop in v_F^eff implies an enhanced quasiparticle mass above H′.

Instead, it is natural to think of Zeeman splitting giving rise to linear-in-H specific heat, which can result from Zeeman splitting of d-wave quasiparticles at sufficiently high fields²⁵. In such a case, the high-field slope ΔC_elec(H)/TH ∼ (v_Fv_Δ)⁻¹, and—assuming a g-factor of 2—our value for this slope, ≈0.16 mJ mol⁻¹ K⁻² T⁻¹, determines α ≈ 0.37 mJ mol⁻¹ K⁻³ (refs 12,25). This violates our established zero-field bound on α by almost a factor of two, and requires a marked drop in the product v_F^effv_Δ^eff over a small field range around H′ for this Zeeman scenario to be internally consistent.

Figure 4b presents this second scenario, with fixed v_Δ (determined from A_c, the prefactor of the square root H) and a field-dependent v_F^eff calculated to fit the low-temperature data. The magnitude of v_F^eff decreases by at least a factor of three from its low-field value, suggesting the sudden onset of a mass enhancement at H′. The phase diagram of YBCO (Fig. 5) supports this picture and provides a scenario for understanding the observed phase transition: in the resistive state, using pulsed magnetic fields above 50 T, quantum oscillations (QO; ref. 26) and resistivity measurements²⁷ have been interpreted in terms of a metal-to-insulator transition (MIT) near YBCO6.47, with a divergent cyclotron mass, m^∗ (ref. 26). In light of Fig. 4b, we propose that this enhanced mass is a field-sensitive phenomenon, which increases rapidly at H′ and drives the system into a Zeeman-dominated regime. We note that v_F^eff/v_Δ ≈ 2/3 above 20 T (see Supplementary Information), a violation of the requirement that v_F ≫ v_Δ in the orbital-scaling regime, providing a further quantitative indication that the high-field regime is physically distinct from the low-field regime.

Figure 5: Phase diagram of YBCO.

The sections represent the H–p plane for T → 0 and the T–p plane for H → 0. Orange/white rectangles represent the range of the present measurements, and the black rectangle represents ref. 16. Orange and white represent the range of d-wave scaling (that is, C_elec/T ∼ H^1/2) and linear-in-H behaviour, respectively. H′ marks the phase transition. Superconductivity (SC) phase boundaries (blue curves) are from refs 11,15. Metal-to-insulator (MIT) boundary (green/yellow) was determined from resistivity²⁷ and QO (ref. 26). Charge density wave (CDW) was established via NMR (ref. 7) (purple, red circle/line) and X-rays^8,30 (pink, blue circle/line, CDW may extend below p = 0.08 (ref. 28)). Spin density wave (red) at H = 0, as determined by neutron scattering⁶ (green squares) and μSR (refs 4,5) (green circles), vanishes near p = 0.08.

A proposed quantum critical point at p = 0.08 (refs 27,28), linked to the high-field mass enhancement²⁶, has been associated in YBCO with the boundary of a spin density wave (SDW) phase seen by means of neutron diffraction and muon spin rotation (μSR; refs 5,6; Fig. 5), whose order is enhanced by magnetic field⁶. Our high-field state may be linked to this SDW and its associated critical point. Indeed, a field-driven transition to a SDW state—coexisting with SC—has been reported in the cuprates, although this observation was in a different material (La_2−xSr_xCuO₄) at a much higher doping (p = 0.14; ref. 29). Unfortunately, the most comprehensive survey of the specific heat of La_2−xSr_xCuO₄ (ref. 21) does not include a sample at a doping that would traverse this reported phase boundary. A neutron scattering or nuclear magnetic resonance (NMR) experiment in YBCO at these dopings and magnetic fields might provide further evidence of SDW order underlying the magnetic-field-driven phase transition that we report here.