Abstract
From the self-organization of the cytoskeleton to the synchronous motion of bird flocks, living matter has the extraordinary ability to behave in a concerted manner1,2,3,4. The Boltzmann equation for self-propelled particles is frequently used in silico to link a system’s meso- or macroscopic behaviour to the microscopic dynamics of its constituents5,6,7,8,9,10. But so far such studies have relied on an assumption of simplified binary collisions owing to a lack of experimental data suggesting otherwise. We report here experimentally determined binary-collision statistics by studying a recently introduced molecular system, the high-density actomyosin motility assay11,12,13. We demonstrate that the alignment induced by binary collisions is too weak to account for the observed ordering transition. The transition density for polar pattern formation decreases quadratically with filament length, indicating that multi-filament collisions drive the observed ordering phenomenon and that a gas-like picture cannot explain the transition of the system to polar order. Our findings demonstrate that the unique properties of biological active-matter systems require a description that goes well beyond that developed in the framework of kinetic theories.
Similar content being viewed by others
Main
Unlike animals that possess interactions such as spatial cognition or hierarchical dispositions14,15,16, the interactions of reconstituted11,12,13,17,18 or synthetic19,20,21,22 model systems stem purely from physical interactions among the constituents. Although weak alignment forces have been proposed to be sufficient for the polar ordering transitions11, no experimental data are available that quantify the interaction rules between the constituents. Owing to the lack of experimental data for such interaction rules, microscopic studies assume either an average rule over the particles in the neighbourhood23,24, or that all binary interactions lead to perfect polar alignment5.
Here we provide the angle-resolved binary-collision statistics for a paradigmatic experimental active system; the actomyosin motility assay. The experimental system consists of only two main components: actin filaments and non-processive motor proteins heavy meromyosin (HMM; refs 11, 12, 13, 25). Actin filaments move on a lawn of HMM by consumption of adenosine triphosphate (ATP) at a constant speed of approximately 4 μm s−1, which is ensured in the experiment by using high ATP concentrations. The orientation of a single filament motion is determined solely by the head, and the motion itself exhibits no long-term directionality, where the randomness of the system is generated by the pushing of the motors.
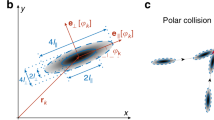
To obtain the binary-collision statistics, the experiments are conducted under dilute conditions with filament densities between 0.005ρc and 0.06ρc, where ρc ≈ 5 filaments μm−2 is the critical density for the disorder–order transition11. Only short filaments with L = 2–5 μm are considered, to ensure that collisions are binary and also that the collision angles can be unambiguously defined, which becomes difficult for longer filaments owing to the intrinsic bending of the filaments. When two filaments encounter each other, for the majority of the collision events the filaments readily cross each other. Despite the frequent crossing events, we observe various tendencies in the binary collisions: polar alignment, anti-polar alignment and events where the filament orientation hardly changes (Fig. 1a–c). To quantify these tendencies we measure the incoming angle θ12 = θ1–θ2 along with the outgoing angle θ12′ = θ1′–θ2′ (Fig. 1d; see Methods). Binary collisions alone are extracted and all non-binary collisions are neglected. All filament densities in the dilute regime demonstrate similar quantitative behaviour for the experimentally obtained binary-collision statistics θ12′(θ12) (Fig. 2a), where unaffected collisions, θ12′ = θ12, are represented by a diagonal line in the diagram. The similarity in the behaviours indicates that there are no significant spatial correlations between the filaments for the dilute densities considered.
a, Scatter plot of θ12′(θ12). Red open squares and blue solid circles represent ρlow = 0.005ρc and ρhigh = 0.06ρc, respectively. Green solid line represents the collisions that are unaffected (θ12′ = θ12). Here, the numbers of collisions investigated are Nlow = 1,113 and Nhigh = 646. b, Incoming angle statistics. Red solid line corresponds to the Boltzmann scattering cylinder for rods with slender-rod assumption L ≫ d. Error bars:  . c, Mean plot of a via binning by θ12. Green dashed line represents unaffected collisions. Indication of weak polar bias where θ12′ < θ12 for highly acute θ12. Error bars: Standard deviation. d, Skewness of θ12′ distribution with respect to θ12. Positive and negative skewness correspond to polar and anti-polar alignment, respectively. Skewness of 2 corresponds to an exponential distribution. In b–d, ρ = ρlow.
. c, Mean plot of a via binning by θ12. Green dashed line represents unaffected collisions. Indication of weak polar bias where θ12′ < θ12 for highly acute θ12. Error bars: Standard deviation. d, Skewness of θ12′ distribution with respect to θ12. Positive and negative skewness correspond to polar and anti-polar alignment, respectively. Skewness of 2 corresponds to an exponential distribution. In b–d, ρ = ρlow.
The distribution P(θ12) of the incoming angle exhibits an asymmetric shape which is consistent with the Boltzmann scattering cylinder for rods8,9 when considering the assumption of slender rods (Supplementary Information), which gives P(θ12) ∝ Γ(θ12) = 2Lv0|sin(θ12/2)| ⋅ |sinθ12| (see red line in Fig. 2b). Here, L denotes the filament length and v0 is the filament speed. The limiting case of slender rods is justified as actin filaments have a length of L = 2–5 μm and a diameter of d ≈ 8 nm. The Boltzmann scattering cylinder Γ describes the frequency of collisions between propelled particles of constant speed as a function of the relative angle θ12, which is derived by geometric considerations. Owing to the large aspect ratio, incoming angles close to 0° and 180° are less likely for slender rods, and the corresponding distribution is asymmetric.
Averaging the experimentally obtained binary-collision statistics θ12′(θ12), we see that although most events for incoming angles θ12 > 80° are indeed largely unaffected by the collision, at highly acute θ12 a clear polar bias can be recognized: θ12′ is smaller than θ12 (Fig. 2c). The distribution of θ12′(θ12) is significantly skewed towards polar outcomes for highly acute θ12 and anti-polar outcomes for θ12 close to 180° (Fig. 2d). Because of this strong skewness, all data points of the experimental binary-collision statistics, and not just the average and standard deviation, are required to make a proper prediction on the existence of transition to polar order. Using the average of the collision statistics can lead to the loss of important information concerning the collision events, and ultimately cause a wrong prediction on the existence of polar order7.
To connect the microscopic dynamics to the meso- or macroscopic pattern formation and ordering transition in active systems, the Boltzmann equation for propelled particles has been successfully applied5,6,7,8,9,10. The Boltzmann equation describes the mesoscopic particle motion and maps the pre-collision states onto the post-collision states, which enables the analytical prediction of the onset to polar order. It determines the time evolution of the one-particle distribution function f(r, θ, t), where r are the coordinates, θ is the particle orientation and t is time:

The streaming term,  , accounts for the movement of particles with velocity
, accounts for the movement of particles with velocity  , where v0 denotes the constant speed and
, where v0 denotes the constant speed and  . Angular fluctuations are described as Dθ∂θ2f (see refs 20, 26), with Dθ denoting the angular diffusion constant. The collision integral,
. Angular fluctuations are described as Dθ∂θ2f (see refs 20, 26), with Dθ denoting the angular diffusion constant. The collision integral,  , captures the effect of binary filament collisions and the filament geometry. It consists a two-particle density f(2)(r, θ1, θ2, t), which can be written in the absence of correlations as f(2)(r, θ1, θ2, t) = f(r, θ1, t)f(r, θ2, t). The collision integral
, captures the effect of binary filament collisions and the filament geometry. It consists a two-particle density f(2)(r, θ1, θ2, t), which can be written in the absence of correlations as f(2)(r, θ1, θ2, t) = f(r, θ1, t)f(r, θ2, t). The collision integral  plays a key role as the experimentally obtained data enter this term, which determines whether a transition to polar order exists or not.
plays a key role as the experimentally obtained data enter this term, which determines whether a transition to polar order exists or not.  can be divided into a loss (−) and a gain (+),
can be divided into a loss (−) and a gain (+),  , (ref. 7):
, (ref. 7):


where we omitted time and space dependencies for brevity. The gain and loss contributions are derived from integrating over all possible pre-collision orientations of the particles. A collision occurs with a frequency given by the Boltzmann collision cylinder for rods, Γ(θ12), and changes the orientation according to θj → θj + ηj(θ12) = θj′, j ∈ {1,2}, where ηj denotes the angular change of the jth particle orientation. For a given relative pre-collision angle θ12, the orientation of particle j changes by ηj(θ12) with probability pj(ηj|θ12)dηj. The experimental scattering statistics (Fig. 2a) is equivalently expressed in terms of pj(ηj|θ12) (Fig. 3a, b; Supplementary Information). If the filaments are indistinguishable, two important symmetry properties of pj need to be satisfied: particle exchange symmetry p1(η1|θ12) = p2(η2|−θ12) and mirror symmetry p1(−η1|θ12) = p1(η1|−θ12), where the same argument applies for p2. Indeed both are obeyed in the experimentally obtained binary-collision statistics of the actomyosin motility assay system (Fig. 3c, d and Supplementary Information). This indicates that experimental uncertainties, such as the narrow filament length distribution, do not influence or bias the binary-collision statistics.
Equations (1)–(3) are now analysed in terms of Fourier modes, where all Fourier coefficients are determined by the comprehensive binary-collision statistics pj (ref. 7). The Fourier representation is a good starting point to derive the homogeneous and linearized equations for the coarse-grained momentum g, ∂tg = ν g. The calculation also yields the coefficients ν in terms of pj. The equations for the momentum become unstable for ν > 0, thus the transition density of polar order corresponds to ν = 0 (refs 5, 26). Specifically, the coefficient  , where
, where  contains the comprehensive binary-collision statistics pj (Fig. 3a, b). See Supplementary Information for the detailed mathematical expressions. Importantly, for the onset of polar order (ν > 0),
contains the comprehensive binary-collision statistics pj (Fig. 3a, b). See Supplementary Information for the detailed mathematical expressions. Importantly, for the onset of polar order (ν > 0),  must be positive.
must be positive.
Using the experimental data (Figs 2b and 3a, b), we find  for binning of Δθ12 = 15° and Δη = 15° (see Supplementary Information for details on the computation of
for binning of Δθ12 = 15° and Δη = 15° (see Supplementary Information for details on the computation of  using experimental data). The negative sign of
using experimental data). The negative sign of  computed from the experimental data is robust against binning of η and θ (Supplementary Information). This implies that the binary-collision description is insufficient to explain the ordering transition in the experimental system for any density ρ, and the isotropic state is linearly stable. This statement is independent of the value of the rotational diffusion constant Dθ as it opposes the formation of polar order, expressed by a negative sign in ν. We test the consistency of our results with analytic predictions for a well-established theoretical model system where rods interact by half-angle alignment (ηj = θi/2 − θj/2; refs 5, 6), which results in
computed from the experimental data is robust against binning of η and θ (Supplementary Information). This implies that the binary-collision description is insufficient to explain the ordering transition in the experimental system for any density ρ, and the isotropic state is linearly stable. This statement is independent of the value of the rotational diffusion constant Dθ as it opposes the formation of polar order, expressed by a negative sign in ν. We test the consistency of our results with analytic predictions for a well-established theoretical model system where rods interact by half-angle alignment (ηj = θi/2 − θj/2; refs 5, 6), which results in  (Supplementary Information), agreeing well with refs 6, 7.
(Supplementary Information), agreeing well with refs 6, 7.
Although we show that polar order cannot be reached when neglecting angular correlations (molecular chaos), small locally aligned filament clusters could still trigger the onset of polar order by binary collisions7,27. To model such weak orientational correlations we write f(2)(r, θ1, θ2, t) = χ(θ12)f(r, θ1, t)f(r, θ2, t), where χ(θ12) characterizes the precursor angular correlations; for χ = 1, angular correlations are absent, leading to the assumption of molecular chaos. Led by recent studies of angular correlations in a self-propelled particle system7, we emulate angular correlations as χ(θ12) = 1 + A/θ12, where A is a free parameter that determines the strength of orientational correlations. For A = 0, correlations are absent, whereas large A values correspond to small, locally aligned filament clusters. We find that using different strengths of angular pair-correlations A does not change the negative sign of the kinetic coefficient (Supplementary Information). This implies that even a collection of pre-formed weakly aligned filaments, which collide accordingly to the experimental data pj (Fig. 3a, b), cannot cause the system to order. It effectively augments the dealigning contributions, causing  to decrease with increasing magnitude of χ. We conclude that, independent of the assumptions of zero noise and molecular chaos, the pattern formation observed in the motility assay cannot be explained solely by a succession of binary filament collisions.
to decrease with increasing magnitude of χ. We conclude that, independent of the assumptions of zero noise and molecular chaos, the pattern formation observed in the motility assay cannot be explained solely by a succession of binary filament collisions.
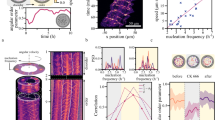
The transition to polar order seen in the experiment can, however, be understood by multi-particle collisions: Already for densities one order of magnitude below the transition density, binary collisions are rare, characterized by the experimentally determined ratio R = nbinary/nall of binary collisions nbinary to all collisions nall (Fig. 4a). At ρ = 0.06ρc less than 10% of all collisions are binary. Thus, for densities close to the transition density ρc, filaments predominantly encounter multi-particle collisions.
a, Ratio R = nbinary/nall of binary collisions nbinary to all collisions nall. Grey shaded region indicates the ordered phase. b–d, Filament length dependence on transition density ρc. b, At filament density ρ ≈ 16 filaments μm−2, long filaments form polar ordered active clusters. White arrows show examples of cluster motion direction. c, For short filaments at the same density as b, no polar order emerges. In b,c, scale bars are 100 μm. d, Log–log plot of ρc(L), showing an approximately quadratic dependence. Solid line shows best fit of L1.71. Error bars: Standard deviation for both ρc and L. Inset: Degree of multi-filament collisions ρcL2 against filament length L.
More importantly, multi-filament collisions are essential for the transition to polar order, which is manifest in the dependence of the transition density on the filament length. At a given filament density ρ ≈ 16 filaments μm−2, long filaments with length Llong = 4–7 μm are able to form polar structures (Fig. 4b), whereas an assay of short filaments with length Lshort = 0.5–3 μm remain in the isotropic state (Fig. 4c). Yet, at a higher concentration ρ ≈ 30 filaments μm−2, short filaments are able to create clusters. At this higher concentration of filaments, the long-filament system is already in the density-wave regime11.
As the exact nature of the length dependence on the transition density ρc indicates the microscopic mechanism of the transition, we systematically vary the average filament lengths from 2–10 μm and determine ρc (Fig. 4d). For a gas of propelled particles, where binary collisions are dominant (equations (1)–(3)), the transition density is defined by ν = 0; hence, ρc is expected to scale with 1/L (see Supplementary Equation 8). Thus, in this slender-rod limit, the collision probability is determined only by the length of the collision partner. Yet, we observe here an approximately quadratic behaviour for ρc(L) (Fig. 4d), ruling out the gas-like picture for this system. At the transition density ρc, the total number of simultaneous collisions for a filament of length L is constant: ρcL2 ≈ 200–300 (Fig. 4d inset). Importantly, this implies that it is the total number of simultaneous collisions and not the filament length itself which defines the order transition.
The presented results challenge our current understanding on the polar ordering transition in active systems. Such polar ordering transition is not determined purely by the number of particles in the system, but rather by the degree of multi-particle collisions. Systems governed by such features could well be described by kinetic models that incorporate collisions of arbitrary numbers of partners28,29 or go beyond Boltzmann’s mean-field assumption of molecular chaos30. The uniqueness of the actomyosin motility assay, which enables access to all microscopic interactions and parameters, sets a quantitative basis for further development of our understanding of ordering phenomena in this diverse class of materials.
Methods
Assay preparation.
We used standard protocols to prepare the actin filaments and heavy meromyosin (HMM) motor proteins. Fluorescently labelled filaments stabilized with Alexa Fluor 488 phalloidin were used to visualize filaments with a fluorescence microscope. Flow chambers built from nitrocellulose-coated coverslips were incubated with HMM (0.05 μg ml−1). Bovine serum albumin was used to passivate the surfaces inside the chamber after the incubation with HMM, then a dilute solution of actin filaments (binary collision: approximately 10–100 nM, filament length dependency: approximately 3–10 μM) was introduced. We added 2 mM ATP to enable the HMM to drive the filaments and a standard antioxidant buffer supplement was used to prevent oxidation of the fluorophore. Filament length was adjusted by shearing. For details of protein and assay chamber preparations, refer to Supplementary Information.
Imaging.
A Leica DMI 6000B inverted microscope was used to acquire data. A ×100 oil objective (NA: 1.4) was used for the binary-collision experiments and a ×40 oil objective (NA: 1.25) for the filament length dependency experiment. Images of resolution 1,344 × 1,024 pixels at a time resolution of 0.13 s were captured with a charge-coupled device (CCD) camera (C4742-95, Hamamatsu) attached to a ×1 (for binary collisions) and ×0.35 (for filament length dependency) camera mount.
Data analysis.
For the binary-collision experiments, filaments are identified by labelling connected components in the binary images and then are skeletonized, using Matlab. A cubic spline fit is applied to the skeletonized filaments to obtain coordinates for the filament contour. The coordinates for the filament head are used to determine θ1,2 and θ1,2′. A collision is defined from when two filaments touch each other, until they are separated. Any collision events involving three or more filaments are classified as non-binary. See Supplementary Information for more details.
References
Karsenti, E. Self-organization in cell biology: A brief history. Nature Rev. Mol. Cell Biol. 9, 255–262 (2008).
Fletcher, D. A. & Mullins, R. D. Cell mechanics and the cytoskeleton. Nature 463, 485–492 (2010).
Couzin, I. D. & Krause, J. Self-organization and collective behavior in vertebrates. Adv. Study Behav. 32, 1–109 (2003).
Vicsek, T. & Zafeiris, A. Collective motion. Phys. Rep. 517, 71–140 (2012).
Bertin, E., Droz, M. & Grégoire, G. Boltzmann and hydrodynamic description for self-propelled particles. Phys. Rev. E 74, 022101 (2006).
Bertin, E., Droz, M. & Grégoire, G. Hydrodynamic equations for self-propelled particles: Microscopic derivation and stability analysis. J. Phys. A 42, 445001 (2009).
Hanke, T., Weber, C. A. & Frey, E. Understanding collective dynamics of soft active colloids by binary scattering. Phys. Rev. E 88, 052309 (2013).
Weber, C. A., Thüroff, F. & Frey, E. Role of particle conservation in self-propelled particle systems. New J. Phys. 15, 045014 (2013).
Thüroff, F., Weber, C. A. & Frey, E. Critical assessment of the Boltzmann approach to active systems. Phys. Rev. Lett. 111, 190601 (2013).
Thüroff, F., Weber, C. A. & Frey, E. Numerical treatment of the Boltzmann equation for self-propelled particle systems. Phys. Rev. X 4, 041030 (2014).
Schaller, V., Weber, C., Semmrich, C., Frey, E. & Bausch, A. R. Polar patterns of driven filaments. Nature 467, 73–77 (2010).
Butt, T. et al. Myosin motors drive long range alignment of actin filaments. J. Biol. Chem. 285, 4964–4974 (2010).
Hussain, S., Molloy, J. E. & Khan, S. M. Spatiotemporal dynamics of actomyosin networks. Biophys. J. 105, 1456–1465 (2013).
Ward, A. J., Sumpter, D. J. T., Couzin, I. D., Hart, P. J. B. & Krause, J. Quorum decision-making facilitates information transfer in fish shoals. Proc. Natl Acad. Sci. USA 105, 6948–6953 (2008).
Nagy, M., Ákos, Z., Biro, D. & Vicsek, T. Hierarchical group dynamics in pigeon flocks. Nature 464, 890–894 (2010).
Attanasi, A. et al. Information transfer and behavioural inertia in starling flocks. Nature Phys. 10, 691–696 (2014).
Zhang, H. P., Be’er, A., Florin, E. L. & Swinney, H. L. Collective motion and density fluctuations in bacterial colonies. Proc. Natl Acad. Sci. USA 107, 13626–13630 (2010).
Sumino, Y. et al. Large-scale vortex lattice emerging from cocollective moving microtubules. Nature 483, 448–452 (2012).
Narayan, V., Ramaswamy, S. & Menon, N. Long-lived giant number fluctuations in a swarming granular nematic. Science 317, 105–108 (2007).
Aranson, I. S., Volfson, D. & Tsimring, L. S. Swirling motion in a system of vibrated elongated particles. Phys. Rev. E 75, 051301 (2007).
Kudrolli, A., Lumay, G., Volfson, D. & Tsimring, L. S. Swarming and swirling in self-propelled polar granular rods. Phys. Rev. Lett. 100, 058001 (2008).
Deseigne, J., Dauchot, O. & Chaté, H. Collective motion of vibrated polar disks. Phys. Rev. Lett. 105, 098001 (2010).
Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I. & Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226–1229 (1995).
Grégoire, G. & Chaté, H. Onset of collective and cohesive motion. Phys. Rev. Lett. 92, 025702 (2004).
Sheetz, M. P., Chasan, R. & Spudich, J. A. ATP-dependent movement of myosin in vitro: Characterization of a quantitative assay. J. Cell Biol. 99, 1867–1871 (1984).
Aranson, I. S. & Tsimring, L. S. Pattern formation of microtubules and motors: Inelastic interaction of polar rods. Phys. Rev. E 71, 050901 (2005).
Weber, C. A., Schaller, V., Bausch, A. R. & Frey, E. Nucleation-induced transition to collective motion in active systems. Phys. Rev. E 86, 030901 (2012).
Ihle, T. Kinetic theory of flocking: Derivation of hydrodynamic equations. Phys. Rev. E 83, 030901 (2011).
Ihle, T. Large density expansion of hydrodynamic theory for self-propelled particles. Preprint at http://arXiv.org/abs/1501.03570 (2015).
Chou, Y.-L. & Ihle, T. Active matter beyond mean-field: Ring-kinetic theory for self-propelled particles. Phys. Rev. E 91, 022103 (2015).
Acknowledgements
This research was supported by the European Research Council in the framework of the Advanced Grant 289714-SelfOrg, Deutsche Forschungsgemeinschaft via project No. B2 within the SFB No. 863, and the German Excellence Initiative via the programme ‘NanoSystems Initiative Munich’ (NIM).
Author information
Authors and Affiliations
Contributions
R.S., C.A.W., E.F. and A.R.B. designed the project. R.S. and A.R.B. performed and designed all experiments. C.A.W. and E.F. theoretically analysed the experimental data. All authors participated in interpreting the experimental and theoretical results and in writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1115 kb)
Rights and permissions
About this article
Cite this article
Suzuki, R., Weber, C., Frey, E. et al. Polar pattern formation in driven filament systems requires non-binary particle collisions. Nature Phys 11, 839–843 (2015). https://doi.org/10.1038/nphys3423
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3423
This article is cited by
-
Collective migration reveals mechanical flexibility of malaria parasites
Nature Physics (2022)
-
Non-reciprocal phase transitions
Nature (2021)
-
Organizing bacterial vortex lattices by periodic obstacle arrays
Communications Physics (2020)
-
C. elegans collectively forms dynamical networks
Nature Communications (2019)
-
Active matter at the interface between materials science and cell biology
Nature Reviews Materials (2017)