Abstract
Single-atom-resolved detection in optical lattices using quantum-gas microscopes1,2 has enabled a new generation of experiments in the field of quantum simulation. Although such devices have been realized with bosonic species, a fermionic quantum-gas microscope has remained elusive. Here we demonstrate single-site- and single-atom-resolved fluorescence imaging of fermionic potassium-40 atoms in a quantum-gas microscope set-up, using electromagnetically-induced-transparency cooling3,4. We detected on average 1,000 fluorescence photons from a single atom within 1.5 s, while keeping it close to the vibrational ground state of the optical lattice. A quantum simulator for fermions with single-particle access will be an excellent test bed to investigate phenomena and properties of strongly correlated fermionic quantum systems, allowing direct measurement of ordered quantum phases5,6,7,8,9 and out-of-equilibrium dynamics10,11, with access to quantities ranging from spin–spin correlation functions to many-particle entanglement12.
Similar content being viewed by others
Main
The ability to observe and control quantum systems at the single-particle level has revolutionized the field of quantum optics over recent decades. At the same time, the possibility to trap atoms in well-controlled engineered environments in optical lattices has proved to be a powerful tool for the investigation of strongly correlated quantum systems13. It was only recently that the great challenge to have full single-site resolution and single-atom control in optical lattices was overcome by the development of quantum-gas microscopes1,2. These have been realized with bosonic 87Rb (refs 1, 2) and 174Yb atoms14. However, until this work and that presented in refs 15, 16, single-site resolution for fermions has remained elusive.
Some of the most interesting effects in many-body quantum systems are due to the properties of strongly interacting Fermi gases. Within solid-state physics, the fermionic nature of the electron is vital to understand a range of phenomena, such as electron pairing in superconductivity, and quantum magnetism (including colossal magnetoresistance). However, some of the properties of many-body fermionic quantum systems are very challenging to compute, even with the most advanced numerical methods, due to the antisymmetric nature of the wavefunction, and the resulting sign problem for quantum Monte Carlo methods17. A quantum simulator for fermions with single-particle resolution would be an excellent test bed to investigate many of the phenomena and properties of strongly correlated fermionic quantum systems. Such a fermionic quantum-gas microscope will provide the possibility to probe quantities that are difficult to access directly, such as spin–spin correlation functions or string order18. It would allow the study of out-of-equilibrium dynamics, the spreading of correlations10 and the build-up of entanglement in many-particle fermionic quantum systems12. It could perform quantum simulation of the Fermi–Hubbard model, which is conjectured to capture the key mechanism behind high-Tc superconductors, allowing researchers to gain insight into electronic properties that could potentially be applied in future materials engineering.
To achieve single-site-resolved detection of individual atoms on the lattice, it is desirable to maximize the fluorescence yield while at the same time maintaining a negligible particle loss rate and preventing the atoms from hopping between lattice sites. These conditions can be efficiently achieved by simultaneously laser cooling the atoms to sub-Doppler temperatures while detecting the fluorescence photons emitted during this process. However, cooling of fermionic alkaline atoms in optical lattices is challenging, as their low mass and small excited-state hyperfine splitting make it more difficult to obtain low temperatures using the standard technique of polarization-gradient cooling.
In this work, we achieved single-atom-resolved fluorescence imaging of 40K using electromagnetically-induced-transparency (EIT) cooling3,4. This technique has been used to efficiently cool trapped ions19 and to manipulate individual neutral atoms in an optical cavity20,21. EIT cooling is similar to grey molasses, recently used to cool atoms and enhance density in free-space atomic samples22,23. Both methods rely on the existence of a spectrally narrow, Fano-like line profile and dark resonances arising from quantum interference in a Λ-like level scheme. In confining potentials with quantized vibrational levels, as is the case in our optical lattice, the narrow absorption line can selectively excite red-sideband transitions that cool the atomic motion by removing one vibrational quantum, while carrier and blue-sideband excitations are suppressed. We present EIT cooling as an alternative to Raman sideband cooling techniques24, which have been applied to image atomic clouds25 and individual atoms26, and which have been used recently by other research groups to achieve single-site imaging of fermionic potassium15 or lithium16, independently of the work presented here.
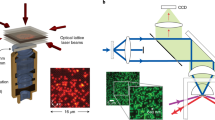
The key component of our experimental set-up is a high-resolution optical microscope2 (Fig. 1a) with numerical aperture (NA) = 0.68, providing a diffraction-limited resolution of 580 nm (full-width at half-maximum, FWHM) at the wavelength of the 4S1/2 → 4P1/2 transition, λD1 = 770.1 nm (D1-line). We prepared a sample of cold fermionic 40K atoms within the focal plane of the microscope (Methods) in a three-dimensional (3D) optical lattice (wavelength λ = 1,064 nm). To implement the EIT cooling scheme, we tuned both coupling and probe beams (Rabi frequencies ΩC and ΩP) close to the D1-line (see atomic level scheme in Fig. 1b). The coupling light was blue-detuned by Δ = 10Γ (Γ = 2π × 6.0 MHz is the linewidth of the 4P excited states) from the F = 9/2 → F′ = 7/2 transition in the lattice; similarly, the probe beam was detuned by Δ = 10Γ from the F = 7/2 → F′ = 7/2 transition. Both pump and probe beams were derived from the same laser by passing the light through an electro-optical modulator (EOM), which generates sidebands at the frequency of the ground-state hyperfine splitting, Δhfs = 2π × 1.2858 GHz. A retroreflected EIT beam in σ+ − σ− configuration is overlapped with each of the optical lattice beams in the x- and y-directions (Fig. 1a) to provide cooling in the horizontal plane. We avoided the use of vertical EIT beams to prevent stray light along the imaging axis. Instead, we used an off-resonant two-photon Raman transition red-detuned by ΔR = 2π × 8 GHz from the 4S1/2 → 4P3/2 transition (D2-line at 767.7 nm) to couple the motional states between the vertical and horizontal lattice axes (Methods). One Raman beam was aligned vertically and the other beam horizontally at a 45° angle between the x- and y-axes (Fig. 1a). We blocked the stray light of the vertical Raman beam with narrowband interference filters (Alluxa) placed in front of the electron multiplying charge-coupled device (EMCCD) camera, which detects fluorescence photons scattered from the EIT beams on the D1 line.
a, Fermionic 40K atoms in an optical lattice were observed using fluorescence detection with a high-resolution optical microscope (NA = 0.68, working distance = 12.8 mm; see ref. 2). The optical lattice (red dots) is composed of two retroreflected beams in the x- and y-axes, and a vertical beam retroreflected from the coated vacuum window. Retroreflected EIT cooling beams (blue) were overlapped with the horizontal optical lattice. Raman beams (green) were used to couple the motional states in the z-axis to the horizontal plane. Atoms were prepared in the focal plane of the microscope objective (inset). b, Level scheme of the relevant states of 40K, with off-resonant Raman beams (green) and near-resonant (detuning Δ) EIT coupling and probe beams (Rabi frequencies ΩC and ΩP, blue) with relative detuning Δhfs + δ.
Our cooling scheme allowed us to image individual 40K atoms in a sparsely populated thermal cloud (Fig. 2a) with an excellent signal-to-noise ratio. We detected on average 1,000(400) (where the number in parentheses denotes the 1σ uncertainty of the last digits) fluorescence photons per atom within an illumination time of 1.5 s using a lattice depth of kB × 245(20) μK (kB is Boltzmann’s constant) on all axes (Methods). Taking into account the collection efficiency of 8.6% of our imaging system (Methods), we calculated a corresponding atomic fluorescence rate of 8(3) × 103 photons s−1. This is large enough to unambiguously identify the presence or absence of an atom for each lattice site (Fig. 2b and Methods); however, it is more than a factor of ten smaller than those obtained in the quantum-gas-microscope set-ups with 87Rb (refs 1, 2). Our measured point-spread function, obtained by averaging 640 fluorescence images of individual atoms (Fig. 2e), has a FWHM of 630(10) nm, close to the diffraction-limited resolution of the microscope objective (Fig. 2d).
a, Fluorescence image of a dilute cloud of 40K atoms in the optical lattice (1.5 s exposure time with EIT cooling). b, 10 μm × 10 μm subsection of a; white dots mark the lattice sites. c, Magnified subsection of a showing an individual atom. d, Horizontal (red circles) and vertical (blue squares) profiles through the centre of the averaged single-atom images shown in e, fitted (horizontal only) with a Gaussian profile (red dashed line). The grey line shows the diffraction-limited point-spread function (PSF) of the microscope objective. e, Measured point-spread function using 640 single-atom images as presented in c, averaged using subpixel shifting1.
To characterize the cooling process, we determined the cloud width (measured using absorption images after rapid release from the lattice potential, Methods) for increasing durations of exposure to the EIT and Raman beams. The cooling results in a decrease of the cloud width to a stationary value, with a time constant of 0.42(2) ms in the horizontal plane and 1.7(2) ms in the vertical direction (Fig. 3a). These time constants correspond to cooling rates of 6(1) ℏω ms−1 and 0.8(3) ℏω ms−1 respectively, where ω = 2π × 300(12) kHz is the spacing of vibrational levels in all three lattice axes. From our measured Rabi frequencies, ΩC = 2π × 4.8(1) MHz, ΩP = 2π × 1.6(1) MHz (Methods), we estimated the width of the narrow line in the Fano profile,  kHz (ref. 4). This value gives an upper limit for the combined scattering rate, γ+/2, on the red sideband for both horizontal axes; our observed cooling (and fluorescence) rates are about a factor of three less. The cooling rate in the vertical direction is different, as there are no vertical EIT beams, instead, cooling is achieved by transferring vibrational excitation quanta via Raman transitions from the vertical axis to the cooled horizontal axes (Methods). Without the Raman beams we observed no cooling in the vertical axis, but instead an increase of the vertical cloud width with time (Fig. 3a), caused by heating due to spontaneously emitted photons from the EIT beams. We estimated a mean number of vibrational quanta of 0.9(1) in each horizontal axis, after 5 ms of cooling, by measuring the steady-state expansion energy with time-of-flight imaging (Methods).
kHz (ref. 4). This value gives an upper limit for the combined scattering rate, γ+/2, on the red sideband for both horizontal axes; our observed cooling (and fluorescence) rates are about a factor of three less. The cooling rate in the vertical direction is different, as there are no vertical EIT beams, instead, cooling is achieved by transferring vibrational excitation quanta via Raman transitions from the vertical axis to the cooled horizontal axes (Methods). Without the Raman beams we observed no cooling in the vertical axis, but instead an increase of the vertical cloud width with time (Fig. 3a), caused by heating due to spontaneously emitted photons from the EIT beams. We estimated a mean number of vibrational quanta of 0.9(1) in each horizontal axis, after 5 ms of cooling, by measuring the steady-state expansion energy with time-of-flight imaging (Methods).
a, Expansion width of the atomic cloud after 1 ms time-of-flight, normalized to the initial width, for varying durations of EIT cooling. Cooling was observed in the y-axis (green squares). In the z-axis, we observed cooling with Raman beams present (green diamonds) and heating without (yellow triangles). b, Expansion width in y-axis as a function of two-photon detuning δ, after 1.5 ms of EIT cooling. c, Atom numbers versus δ, after 1.5 ms (red circles), 30 ms (blue triangles) and 300 ms (orange diamonds) of EIT cooling, measured with absorption imaging. d, Integrated fluorescence counts versus δ during exposure times of 1.5 ms (red circles), 30 ms (blue triangles), 300 ms (orange diamonds) and 2,000 ms (grey squares) during EIT cooling. Each datapoint in a–d is the average of five independent measurements, and the error bars represent the standard deviation.
We studied the characteristics of EIT cooling in our experiment by measuring the cloud width, after 1.5 ms of cooling, as a function of the two-photon detuning δ. On resonance, δ = 0, cooling works most efficiently (Fig. 3b), as the atoms are pumped into the dark state and their lifetime is significantly enhanced (Fig. 3c). However, at negative detuning, δ < 0, we predominantly drive carrier and blue-sideband transitions which heat the atoms (Fig. 3b). For δ ≠ 0, heating resulted in atom loss over timescales of milliseconds. Maximizing the number of fluorescence photons for the single-atom imaging necessitates a compromise between a long lifetime (atoms in the dark state) and a large scattering rate. This can be seen in a shift of the maximum of fluorescence counts with increasing accumulation time (Fig. 3d), from the position of strong heating (δ < 0) towards resonance (δ = 0), where most efficient cooling is achieved. Note that Fig. 3c and d compare the atom number and the fluorescence counts of the complete cloud without layer preparation, to match the conditions of Fig. 3a and b. However, the spatially varying light shift due to the Gaussian intensity profile of the lattice beams causes a position-dependent detuning Δ. As a consequence, optimum conditions for EIT cooling are met only in the central 70 × 70 lattices sites, where Δ changes by less than 20 MHz. This fact causes loss of atoms outside the area of most efficient cooling, resulting in a reduced lifetime for the full cloud of 6.6(5) s. The lifetime of the atoms inferred by measuring fluorescence from the central 70 × 70 lattice sites is 30(4) s (see Supplementary Fig. 1).
We investigated in more detail to what extent the atoms are lost and move in the lattice during the imaging process. For this purpose, we recorded two successive fluorescence images of the same atoms with 500 ms exposure time each, and a 500 ms separation between the two images. From each of the images we determined the atom distribution on the lattice using a deconvolution algorithm (Methods), providing us with a binary map of the lattice site occupation. To estimate hopping, we calculated the fraction of atoms, h, that appeared on previously empty lattice sites as well as the fraction of atoms lost, l, from the first to the second image (Fig. 4). Varying δ, we measured hopping fractions as low as h = 3.5(1.5)% and observed that l increased from 4.2(1.9)% at δ = 0 to larger values for δ ≠ 0. We attribute this increased loss to the less efficient cooling due to the absence of a dark state, as discussed above (Fig. 3c). Even at δ = 0, both loss and hopping could result from off-resonant excitation by the EIT and Raman beams to the 4P1/2 and 4P3/2 excited states. Both 4P states experience a light shift more than five times greater and opposite to the ground-state light shift, due to the proximity of the lattice wavelength to the 4P → 3D resonance at 1,180 nm. In our case, the use of blue-detuned EIT beams ensures that the atoms preferentially scatter off a trapped dressed state. However, an atom resonantly excited to the 4P state experiences a repulsive potential which causes the excited-state wavepacket to expand rapidly in space. During the subsequent spontaneous emission the atoms can decay into a high vibrational state or a high band in which the atoms are no longer bound to the lattice sites. These hot atoms can now move across the lattice, and then potentially be recooled and bound to a different lattice site. We are currently investigating this heating process in more detail using numerical simulations of the full quantum evolution of an atom on a few lattice sites.
Fraction of atoms, h, appearing (blue squares) on a previously empty site in the second of two successive fluorescence images (500 ms exposure time, 500 ms delay between the two images), normalized to the number of atoms in the first image. Also shown is the fraction of atoms, l, that has disappeared between the two images (red dots). The panels show binary maps of the lattice site occupations of the first (red circles) and second image (blue squares). They show regions of 20 × 20 lattice sites; however, the data is analysed in a region of 70 × 70 sites. Each data point results from the average of ten fluorescence images; the error bars represent the standard deviation.
The single-site-resolved detection of 40K in an optical lattice will open the path to the study of strongly correlated fermionic quantum systems with unprecedented insight into their properties. In particular, our new technique will allow the study of strongly correlated phases in the Fermi–Hubbard model, for example, counting thermal excitations in fermionic Mott insulators27,28 and directly probing local entropy distributions2, or detecting the propagation of correlations after quenches10. The quantum-gas microscope will also enable manipulation of the system on a local scale with single-site addressing resolution29, allowing deterministic preparation of non-thermal initial states30 and probing the ensuing dynamics. This would allow, for example, further investigation of intriguing phenomena in Luttinger liquid theory, such as spin–charge separation31 and the growth of many-body spatial entanglement12. The high-resolution microscope could also be used to implement proposals for removing high-entropy regions by locally modifying the confining potential32 to attain low-entropy states. The fermionic quantum-gas microscope is an ideal tool to detect the onset of antiferromagnetic ordering5,6,7,8,9 with single-site resolution, by directly measuring the spin–spin correlations. In different lattice geometries these measurements would allow the study of, for example, both equilibrium properties and out-of-equilibrium dynamics in frustrated spin systems11.
Methods
Loading of 40K atoms into the optical lattice.
Our experimental sequence started with an atomic beam of 40K produced by a 2D magneto-optical trap (MOT) loaded from 10−7 mbar of potassium vapour (our atomic source is enriched to 3% 40K). This atomic beam passes through a differential pumping section to a standard 3D MOT, which captures 2 × 108 atoms in 4 s. The atoms were further cooled in an optical molasses and loaded into an optical dipole trap formed by two beams of 100 W each (beam radius w0 = 150 μm, wavelength 1,070 nm) crossing at an angle of 15°. The atoms were then loaded into a translatable optical tweezer (beam radius w0 = 50 μm, 18 W power) and moved 13 cm within 1.5 s to within the field-of-view of the high-resolution microscope2. We initially transferred 1 × 106 40K atoms from the single-beam trap into a crossed optical dipole trap, which is formed by the optical lattice beams with their retroreflectors blocked by mechanical shutters, and evaporatively cooled the atoms to T = 4.0(1) μK. We then transferred the sample into the vertical optical lattice (beam radius w0 = 60 μm) and subsequently switched on both horizontal optical lattices (w0 = 75 μm) with the retroreflectors unblocked. The lattice depth was determined by measuring the frequency of the blue-sideband transitions in the lattice using Raman transitions. Driving this sideband results in an increase of the cloud width after time-of-flight. The error of the lattice depth cited in the main text is the 1/e-width of the excitation peak of the spectrum.
Preparation of 2D atomic samples.
To prepare a thin sample within the focal plane of the microscope, we used a position-dependent microwave transition in a vertical magnetic field gradient2 of ∂B/∂z = 80 G cm−1. This gradient results in a shift of the ground-state hyperfine transition |F = 9/2, mF = −9/2〉 → |F = 7/2, mF = −7/2〉 of 20 kHz μm−1. We initially optically pumped the atoms into the |F = 9/2, mF = −9/2〉 state while holding them in a shallow 3D optical lattice, before applying a microwave sweep (HS1-pulse29 of 5 kHz width) to transfer atoms out of one selected layer into the |F = 7/2, mF = −7/2〉 state. All atoms remaining in F = 9/2 were then removed using a circularly polarized resonant laser beam on the F = 9/2 → F′ = 11/2 cycling transition of the D2 line. The microwave transfer and removal processes have an overall efficiency of >90%, resulting in residual atoms in the F = 7/2 manifold across all layers. To remove these atoms, we optically pumped the atoms back to the initial |F = 9/2, mF = −9/2〉 state and again performed a microwave transfer followed by a removal pulse. Using this technique, we were able to prepare about 100 atoms in a single layer of the 3D optical lattice, with a negligible population in other layers. Note that for the images in Fig. 2, we prepared two adjacent layers within the depth of focus of the imaging system, to increase the number of atoms visible. For the data sets presented in Fig. 3, we used absorption images of the full atomic cloud, without single-layer preparation. The atoms are initially in F = 9/2, but once the EIT cooling beams are switched on, the population is predominantly in state F = 7/2.
Analysis of fluorescence images.
To analyse our fluorescence images, we used procedures and computer algorithms based on earlier work2. The precise orientation of the lattice angles, 47.599(3)° and −42.833(3)° with respect to the horizontal baseline of the Fig. 2a, b, and the magnification (5.133 pixels on the CCD camera correspond to λ/2 at the atoms; λ = 1,064 m is the lattice wavelength) were determined by evaluating the mutual distances between 600 isolated atoms from several fluorescence images (see Supplementary Information of ref. 2). Lattice angles and spacings were taken as the input for our deconvolution algorithm2, which uses the averaged point-spread function from Fig. 2e to determine the occupation of the lattice sites. To estimate the average fluorescence rate, we summed the number of counts from a 3 × 3 pixel area centred on each occupied lattice site, and converted this value to a photon number. The resulting histogram of the detected photon number follows a Gaussian distribution of mean 1,000 and standard deviation of 400. The same analysis performed on the empty lattice sites yielded a photon number of less than 200.
Our imaging system has a total fluorescence collection efficiency of 8.6%, given by the objective’s solid angle of Ω/(4π) = 13%, the 80% transmission through the objective, lenses and interference filters, and the 83% quantum efficiency of the EMCCD camera (Andor iXon 897).
Characterization of EIT cooling.
We determined the kinetic energy of a cloud of atoms in time-of-flight measurements after a rapid release from the lattice potential. The initial change in kinetic energy due to the EIT and Raman beams was different for the horizontal and vertical axes, with a horizontal cooling rate of 83(14) μK ms−1 during the first 150 μs and a vertical cooling rate of 12(4) μK ms−1 during the first 400 μs. After a hold time of 5 ms with EIT cooling, the atoms maintained constant horizontal and vertical expansion energies of 10.0(2) μK and 14.8(2) μK. These kinetic energies correspond to mean excitation numbers of 0.9(1) and 1.6(1), respectively, for a harmonic oscillator potential with a trap frequency ω = 2π × 300(12) kHz.
We determined the combined Rabi frequencies of all EIT beams by measuring the off-resonant scattering rate of one beam, with the EOM switched off. The coupling and probe beam Rabi frequencies, ΩC = 2π × 4.8(1) MHz and ΩP = 2π × 1.6(1) MHz, are determined by the modulation depth of the EOM (25% of the power in the first sideband) and by taking into account the transition strengths. The values of the Rabi frequencies do not take into account the fact that there could be different distributions of the magnetic sublevels during this measurement compared with EIT cooling in the lattice.
Raman coupling of motional axes.
In our set-up, we achieved cooling of the vertical axis by transferring its vibrational excitation quanta, via Raman transitions, to the cooled horizontal axes33. We used two Raman beams of identical frequency, such that the exchange of vibrational quanta between two axes is a resonant two-photon process. The Rabi frequency for the transition |nx, nz + 1〉 → |nx + 1, nz〉 can be calculated as ΩR = Ω0〈nx + 1, nz |eiδk⋅r| nx, nz + 1〉, where nx and nz are the vibrational quantum numbers, δ k = k1 − k2 is the momentum transfer from the Raman beams, and Ω0 is the two-photon Rabi frequency of the carrier transition. Expanding the exponential yields  , where we have used the Lamb–Dicke factors
, where we have used the Lamb–Dicke factors  For our parameters, ηx = 0.118(2), ηz = 0.168(3), with
For our parameters, ηx = 0.118(2), ηz = 0.168(3), with  nm the width of the ground-state wavepacket of the harmonic oscillator in directions j = x, z; m is the mass of a 40K atom. We estimate a Rabi frequency of ΩR = 2π × 27(2) kHz by measuring how the vertical expansion width after 0.5 ms of cooling changes as a function of the detuning between the two Raman beams.
nm the width of the ground-state wavepacket of the harmonic oscillator in directions j = x, z; m is the mass of a 40K atom. We estimate a Rabi frequency of ΩR = 2π × 27(2) kHz by measuring how the vertical expansion width after 0.5 ms of cooling changes as a function of the detuning between the two Raman beams.
References
Bakr, W. S., Gillen, J. I., Peng, A., Fölling, S. & Greiner, M. A quantum gas microscope for detecting single atoms in a Hubbard-regime optical lattice. Nature 462, 74–77 (2009).
Sherson, J. F. et al. Single-atom-resolved fluorescence imaging of an atomic Mott insulator. Nature 467, 68–72 (2010).
Morigi, G., Eschner, J. & Keitel, C. H. Ground state laser cooling using electromagnetically induced transparency. Phys. Rev. Lett. 85, 4458–4461 (2000).
Morigi, G. Cooling atomic motion with quantum interference. Phys. Rev. A 67, 033402 (2003).
Snoek, M., Titvinidze, I., Töke, C., Byczuk, K. & Hofstetter, W. Antiferromagnetic order of strongly interacting fermions in a trap: Real-space dynamical mean-field analysis. New J. Phys. 10, 093008 (2008).
Paiva, T., Scalettar, R., Randeria, M. & Trivedi, N. Fermions in 2D optical lattices: Temperature and entropy scales for observing antiferromagnetism and superfluidity. Phys. Rev. Lett. 104, 066406 (2010).
Simon, J. et al. Quantum simulation of antiferromagnetic spin chains in an optical lattice. Nature 472, 307–312 (2011).
Greif, D., Uehlinger, T., Jotzu, G., Tarruell, L. & Esslinger, T. Short-range quantum magnetism of ultracold fermions in an optical lattice. Science 340, 1307–1310 (2013).
Hart, R. A. et al. Observation of antiferromagnetic correlations in the Hubbard model with ultracold atoms. Nature 519, 211–214 (2015).
Cheneau, M. et al. Light-cone-like spreading of correlations in a quantum many-body system. Nature 481, 484–487 (2012).
Eisert, J., Friesdorf, M. & Gogolin, C. Quantum many-body systems out of equilibrium. Nature Phys. 11, 124–130 (2015).
Pichler, H., Bonnes, L., Daley, A. J., Läuchli, A. M. & Zoller, P. Thermal versus entanglement entropy: A measurement protocol for fermionic atoms with a quantum gas microscope. New J. Phys. 15, 063003 (2013).
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008).
Miranda, M., Inoue, R., Okuyama, Y., Nakamoto, A. & Kozuma, M. Site-resolved imaging of ytterbium atoms in a two-dimensional optical lattice. Phys. Rev. A 91, 063414 (2015).
Cheuk, L. W. et al. A quantum gas microscope for fermionic atoms. Phys. Rev. Lett. 114, 193001 (2015).
Parsons, M. F. et al. Site-resolved imaging of fermionic 6Li in an optical lattice. Phys. Rev. Lett. 114, 213002 (2015).
Troyer, M. & Wiese, U.-J. Computational complexity and fundamental limitations to fermionic quantum Monte Carlo simulations. Phys. Rev. Lett. 94, 170201 (2005).
Endres, M. et al. Observation of correlated particle-hole pairs and string order in low-dimensional Mott insulators. Science 334, 200–203 (2011).
Roos, C. F. et al. Experimental demonstration of ground state laser cooling with electromagnetically induced transparency. Phys. Rev. Lett. 85, 5547–5550 (2000).
Mücke, M. et al. Electromagnetically induced transparency with single atoms in a cavity. Nature 465, 755–758 (2010).
Kampschulte, T. et al. Electromagnetically-induced-transparency control of single-atom motion in an optical cavity. Phys. Rev. A 89, 033404 (2014).
Fernandes, D. R. et al. Sub-Doppler laser cooling of fermionic 40 K atoms in three-dimensional gray optical molasses. Europhys. Lett. 100, 63001 (2012).
Grier, A. T. et al. Λ-enhanced sub-Doppler cooling of lithium atoms in D1 gray molasses. Phys. Rev. A 87, 063411 (2013).
Hamann, S. E. et al. Resolved-sideband Raman cooling to the ground state of an optical lattice. Phys. Rev. Lett. 80, 4149–4152 (1998).
Patil, Y. S., Chakram, S., Aycock, L. M. & Vengalattore, M. Nondestructive imaging of an ultracold lattice gas. Phys. Rev. A 90, 033422 (2014).
Lester, B. J., Kaufman, A. M. & Regal, C. A. Raman cooling imaging: Detecting single atoms near their ground state of motion. Phys. Rev. A 90, 011804 (2014).
Jördens, R., Strohmaier, N., Günter, K., Moritz, H. & Esslinger, T. A Mott insulator of fermionic atoms in an optical lattice. Nature 455, 204–207 (2008).
Schneider, U. et al. Metallic and insulating phases of repulsively interacting fermions in a 3D optical lattice. Science 322, 1520–1525 (2008).
Weitenberg, C. et al. Single-spin addressing in an atomic Mott insulator. Nature 471, 319–324 (2011).
Fukuhara, T. et al. Quantum dynamics of a mobile spin impurity. Nature Phys. 9, 235–241 (2013).
Kollath, C., Schollwöck, U. & Zwerger, W. Spin-charge separation in cold Fermi gases: A real time analysis. Phys. Rev. Lett. 95, 176401 (2005).
Bernier, J.-S. et al. Cooling fermionic atoms in optical lattices by shaping the confinement. Phys. Rev. A 79, 061601(R) (2009).
Steinbach, J., Twamley, J. & Knight, P. L. Engineering two-mode interactions in ion traps. Phys. Rev. A 56, 4815–4825 (1997).
Acknowledgements
We thank G. Morigi, A. Daley and A. Buyskikh for fruitful discussions. We acknowledge the contribution of A. Schindewolf, N. Sangouard and J. Hinney during the construction of the experiment. We acknowledge support by EU (ERC-StG FERMILATT, SIQS, Marie Curie Fellowship to E.H.), EPSRC, Scottish Universities Physics Alliance (SUPA).
Author information
Authors and Affiliations
Contributions
E.H., J.H., D.A.C., B.P. and S.K. performed the experiments and data analysis. All authors contributed to the design and set-up of the experiment and to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 166 kb)
Rights and permissions
About this article
Cite this article
Haller, E., Hudson, J., Kelly, A. et al. Single-atom imaging of fermions in a quantum-gas microscope. Nature Phys 11, 738–742 (2015). https://doi.org/10.1038/nphys3403
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3403
This article is cited by
-
Quantized valley Hall response from local bulk density variations
Communications Physics (2023)
-
An unsupervised deep learning algorithm for single-site reconstruction in quantum gas microscopes
Communications Physics (2023)
-
Quantum simulations with ultracold atoms in optical lattices: past, present and future
Journal of the Korean Physical Society (2023)
-
Holographic imaging of an array of submicron light scatterers at low photon numbers
Applied Physics B (2023)
-
A scheme to create and verify scalable entanglement in optical lattice
npj Quantum Information (2022)