Abstract
Heisenberg interactions are ubiquitous in magnetic materials and play a central role in modelling and designing quantum magnets. Bond-directional interactions1,2,3 offer a novel alternative to Heisenberg exchange and provide the building blocks of the Kitaev model4, which has a quantum spin liquid as its exact ground state. Honeycomb iridates, A2IrO3 (A = Na, Li), offer potential realizations of the Kitaev magnetic exchange coupling, and their reported magnetic behaviour may be interpreted within the Kitaev framework. However, the extent of their relevance to the Kitaev model remains unclear, as evidence for bond-directional interactions has so far been indirect. Here we present direct evidence for dominant bond-directional interactions in antiferromagnetic Na2IrO3 and show that they lead to strong magnetic frustration. Diffuse magnetic X-ray scattering reveals broken spin-rotational symmetry even above the Néel temperature, with the three spin components exhibiting short-range correlations along distinct crystallographic directions. This spin- and real-space entanglement directly uncovers the bond-directional nature of these interactions, thus providing a direct connection between honeycomb iridates and Kitaev physics.
Similar content being viewed by others
Main
Iridium (IV) ions with pseudospin-1/2 moments form in Na2IrO3, a quasi-two-dimensional (2D) honeycomb network, which is sandwiched between two layers of oxygen ions that frame edge-shared octahedra around the magnetic ions and mediate superexchange interactions between neighbouring pseudospins (Fig. 1a). Owing to the particular spin–orbital structure of the pseudospin5,6, the isotropic part of the magnetic interaction is strongly suppressed in the 90° bonding geometry of the edge-shared octahedra2,3, thereby allowing otherwise subdominant bond-dependent anisotropic interactions to play the main role and manifest themselves at the forefront of magnetism. This bonding geometry, common to many transition-metal oxides, in combination with the pseudospin that arises from strong spin–orbit coupling gives rise to an entirely new class of magnetism beyond the traditional paradigm of Heisenberg magnets. On a honeycomb lattice, for instance, the leading anisotropic interactions take the form of the Kitaev model3, which is a rare example of exactly solvable models with non-trivial properties such as Majorana fermions and non-Abelian statistics, and with potential links to quantum computing4.
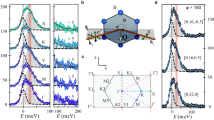
a, Honeycomb layers of Ir4+ in the monoclinic Bravais lattice. Green, yellow and blue planes show Ir2O6 plaquettes normal to the local x-, y- and z-axes (black arrows), respectively, which point along three nearest-neighbour Ir–O bonds in an octahedron. Ir–Ir bonds are labelled following the plaquettes they belong to. Na+ is not shown for clarity. Blue arrows show the spins in the static zigzag order propagating along the b direction. Spins are antiparallel between the layers (not shown). b, Illustration of the scattering geometry. Shown in blue is the scattering plane defined by the incident (ki) and outgoing (kf) wavevector (red arrows). Green arrows show the X-ray polarizations. The azimuth, Ψ, is defined as the angle between the a-axis and the scattering plane. c, Ψ-dependence of the magnetic Bragg peak (blue filled circle) intensity at (0, 1, 3.5) measured in the σ–π′ channel. The black hexagon is the Brillouin zone of the honeycomb net. The red solid line shows the best fitting result to the data with Θ = 44.3°, with a standard error of ±1.24°. We note that the actual error may be larger owing to systematic errors arising from factors such as changes in the beam footprint on the sample. Green and blue lines shows the calculated Ψ dependence for Θ = 40° and 50°, respectively. d–f, H, K and L scans, respectively, of the magnetic Bragg peak at (0, 1, 6.5) for selected temperatures. g, Temperature dependence of the correlation lengths along the a-, b- and c-axes from Gaussian fitting to the scans. Error bars represent the standard deviation in the fitting procedure. The solid lines are guides to the eye.
Realization of the Kitaev model is now being intensively sought out in a growing number of materials7,8,9,10,11,12,13, including 3D extensions of the honeycomb Li2IrO3, dubbed ‘hyper-honeycomb’7 and ‘harmonic-honeycomb’8, and 4d transition-metal analogues such as RuCl3 (ref. 12) and Li2RhO3 (ref. 13). Although most of these are known to magnetically order at low temperature, they exhibit a rich array of magnetic structures, including zigzag14,15,16, spiral17 and other more complex non-coplanar structures18,19 that are predicted to occur in the vicinity of the Kitaev quantum spin liquid (QSL) phase20,21,22,23, which hosts many degenerate ground states frustrated by three bond-directional Ising-type anisotropies. All of these magnetic orders are captured in an extended version of the Kitaev model written as

which includes, in addition to the Kitaev term K, the Heisenberg exchange J, which may be incompletely suppressed in the superexchange process and/or arise from a direct exchange process21, and the symmetric off-diagonal exchange term Γ, which is symmetry-allowed even in the absence of lattice distortions23,24,25. This ‘minimal’ Hamiltonian couples pseudospins S (hereafter referred to as ‘spin’) only on nearest-neighbour bonds 〈ij〉, neglecting further-neighbour couplings, which may be non-negligible. The bond-directional nature of the K and Γ terms is reflected in the spin components [α ≠ β ≠ γ ∈ (x, y, z)] which they couple for a given bond (γ ∈ x-, y-, z-bonds; Fig. 1a). For example, the K term couples only the spin component normal to the Ir2O6 plaquette containing the particular bond. Despite these extra terms that may account for finite-temperature magnetic orders in the candidate materials, the fact that the Kitaev QSL phase has a finite window of stability against these perturbations20,25 calls for investigation of competing phases and a vigorous search for the Kitaev QSL phase.
Although the notion of magnetic frustration induced by competing bond-directional interactions is compelling, it remains a theoretical construct without an existence proof for such interactions in a real-world material. Moreover, theories for iridium compounds based on itinerant electrons suggest alternative pictures26,27,28. In principle, measurement of the dynamical structure factor through inelastic neutron scattering (INS) or resonant inelastic X-ray scattering (RIXS) provides the most direct access to the Hamiltonian describing the magnetic interactions. However, a fully momentum- and energy-resolved dynamical structure factor thus far remains elusive for any of the candidate materials; RIXS suffers from insufficient energy resolution29 and INS is at present limited by unavailability of large-volume single crystals15. In this Letter, we take a new approach using diffuse magnetic X-ray scattering to provide direct evidence for predominant bond-directional interactions in Na2IrO3 through the measurement of equal-time correlations of spin components above the ordering temperature (TN = 12–15 K, see Supplementary Fig. 1).
We start by establishing the spin orientation in the static zigzag order14,15,16 below TN, as shown in Fig. 1a, using standard resonant magnetic X-ray diffraction. In this measurement, the X-ray polarization projects out a certain spin component; the intensity depends on the spin orientation through the relation I ∝ | kf ⋅ S | 2 for the σ–π′ channel measured, where kf is the scattered X-ray wavevector (Fig. 1b). Figure 1c shows the intensity variation as the sample is rotated about the ordering wavevector Q = (0, 1, 3.5) by an azimuthal angle Ψ, which causes S to precess around Q. Earlier studies14,16 have established that S is constrained to lie in the ac-plane, so this measurement of I(Ψ) determines the spin orientation by resolving the tilting angle Θ of S with respect to the a-axis. The best fitting result with Θ = 44.3° indicates that the magnetic easy axis is approximately half way between the cubic x- and y-axes (Fig. 1a). This static spin orientation is a compromise among all anisotropic interactions present in the system, and is strongly tied to the magnetic structure because of their bond-directional nature. To see this point, consider, for example, the K term: in the zigzag structure propagating along the b direction, where the spins are antiferromagnetically aligned on the z-bond and ferromagnetically aligned on the x-bond and y-bond, a ferromagnetic (antiferromagnetic) K favours spins pointing perpendicular to (along) the z-axis for a pair of spins on the z-bond, and along (perpendicular to) the x-axis and y-axis for the pairs on the x-bond and y-bond, respectively.
The zigzag order is one of the many magnetic states (including the aforementioned spiral and non-coplanar structures) that are classically degenerate in the pure Kitaev limit30 and comprise the micro-states in the QSL phase. Away from the pure Kitaev limit, depending on their energy separations, signatures of other magnetic states and their associated magnetic anisotropies may become observable in the paramagnetic phase through diffuse magnetic scattering. In particular, zigzag orders propagating in two other directions, ±120° rotated from the static one, are expected for a honeycomb net with C3 symmetry. (The actual 3D crystal structure has an only approximate C3 symmetry because of a monoclinic distortion, which singles out one propagation direction for the long-range ordered state (along b direction) out of the three possible under the ideal C3 symmetry15.)
With other magnetic correlations possibly emerging at high temperature in mind, we follow the temperature evolution of the zigzag order. Figure 1d–f shows H, K and L scans, respectively, of the magnetic Bragg peak at Q = (0, 1, 6.5) for selected temperatures. Figure 1g shows the correlation lengths along the a-, b- and c-axes as a function of temperature. As the temperature increases above TN, the zigzag correlations diminish rather isotropically, despite dominant 2D couplings in the honeycomb net. This 3D characteristic of the magnetic correlations contrasts with that of the quasi-2D Heisenberg antiferromagnet Sr2IrO4, which exhibits 2D long-range correlations well above TN (ref. 31), and implies that the critical temperature in Na2IrO3 is limited by the anisotropic interactions rather than the interlayer coupling; the Mermin–Wagner theorem requires either the symmetry to be lower than SU(2) or the dimension to be higher than 2D for a finite-temperature phase transition. The zigzag correlations survive on a length scale of several nanometres (approximately three unit cells wide) above TN, but the peak intensities drop by two orders of magnitude. To isolate such small signals from the background, we used an experimental set-up that maximizes the signal-to-noise ratio, as described in the Methods.
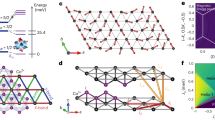
Figure 2a maps the diffuse scattering intensity over a region in momentum space encompassing a full Brillouin zone of the honeycomb net, at several different Ψ angles to resolve the spin components (see Supplementary Fig. 2). These maps integrate the dynamic structure factor over the range 0 ≤ ω ≤ 100 meV, covering the entire range of magnetic excitations, and serve as an excellent approximation for the equal-time correlation  (α = x, y, z). When averaged over the three spin components, the intensity map (Fig. 2c) indeed shows three zigzag correlations above TN, with peaks at Q = ±(0, 1), ±(0.5, 0.5) and ±(0.5, −0.5) of equal intensities, confirming the near-ideal C3 symmetry. However, the spin-component-resolved maps, shown in Fig. 2b, manifestly break the C3 symmetry. The system is left invariant only when C3 rotation is performed simultaneously in the real space and in the spin space—that is, cyclic permutation of spin indices. This ‘global’ C3 symmetry implies a strong entanglement between the real space and the spin space. Specifically, the full azimuthal dependence of each zigzag state, shown in Fig. 2d, closely follows the curves simulated for spin orientation fixed relative to the propagation direction, as depicted in Fig. 2e. In other words, specifying a spin component amounts to fixing the momentum direction and vice versa. This one-to-one correspondence between the spin space and the real space is a direct consequence of the bond-dependent nature of the anisotropic exchange terms.
(α = x, y, z). When averaged over the three spin components, the intensity map (Fig. 2c) indeed shows three zigzag correlations above TN, with peaks at Q = ±(0, 1), ±(0.5, 0.5) and ±(0.5, −0.5) of equal intensities, confirming the near-ideal C3 symmetry. However, the spin-component-resolved maps, shown in Fig. 2b, manifestly break the C3 symmetry. The system is left invariant only when C3 rotation is performed simultaneously in the real space and in the spin space—that is, cyclic permutation of spin indices. This ‘global’ C3 symmetry implies a strong entanglement between the real space and the spin space. Specifically, the full azimuthal dependence of each zigzag state, shown in Fig. 2d, closely follows the curves simulated for spin orientation fixed relative to the propagation direction, as depicted in Fig. 2e. In other words, specifying a spin component amounts to fixing the momentum direction and vice versa. This one-to-one correspondence between the spin space and the real space is a direct consequence of the bond-dependent nature of the anisotropic exchange terms.
a, Intensity plots in the HK-plane (L varying between 6.5 and 7) measured at T = 17 K for selected azimuth angles summing π–σ′ and π–π′ channels, sensitive to spin components parallel to ki and perpendicular to the scattering plane, respectively. For example, Ψ = 0° measures the sum of correlations Sxx and Syy. The dashed hexagon indicates the first Brillouin zone of the honeycomb net. b, Spin-component-resolved equal-time correlations extracted from a. c, Spin-component-integrated equal-time correlations extracted from a. Peaks are located at Q = ±(0, 1), ±(0.5, 0.5), and ±(0.5, −0.5). d, Ψ-dependence of the diffuse peak intensities for Samples 1 (open symbol) and 2 (closed symbol). Solid lines show the calculated Ψ-dependence for x-, y- and z-zigzag states shown in e for the π–σ′ and π–π′ polarization channels summed. e, Zigzag orders propagating along three equivalent directions. Blue zigzag is the static structure, and green and yellow zigzags are generated by 120° rotation of the blue zigzag.
Qualitatively, it is immediately seen that the anisotropic interactions dominate over the isotropic interactions and the system is very far away from the pure Heisenberg limit, in which case the spatial correlations must be spin-component-independent with three zigzag peaks having equal intensities by symmetry (as in the spin-averaged correlation shown in Fig. 2c preserving C3 symmetry). A measure of how close the system is to either the Heisenberg or the Kitaev limits is provided by the intensity ratio of the weakest peak to the two bright peaks in the spin-component-resolved correlations (Fig. 2b). To quantify this measure, represented by a variable linearly interpolating between these two limits, ξ, requires specifying the Hamiltonian, which is not precisely known. For an estimation at a semi-quantitative level, we adopt a simple Hamiltonian that neglects all anisotropic terms beyond the K term. (This in turn requires including further-neighbour Heisenberg couplings J2 and J3 to stabilize the zigzag order32, which we take to be equal to J1 for simplicity.) Figure 3 shows the simulated patterns for selected ξ. It is clear that the observed diffuse pattern is consistent with the simulated pattern for the large ξ limit. In fact, the observed intensity ratio of ≍0.2 is even smaller than calculated (Fig. 3) for the largest ξ in the zigzag phase, which confirms the predominant anisotropic interactions.
The Kitaev–Heisenberg model including up to third nearest-neighbour Heisenberg interactions was considered. ξ interpolates between the pure Heisenberg model and the pure Kitaev model via J1 = J2 = J3 = 1 − ξ and K = −ξ. A ferromagnetic K with finite J1, J2 and J3 stabilizes the zigzag state for most values of ξ. The black curve shows the spectral asymmetry, defined as the ratio of spectral weight at Q = (0.5, 0.5) to that at Q = (0, 1). Images show equal-time correlations  obtained by exact diagonalization using a 24-site cluster and plotted in the extended Brillouin zone for selected ξ. The correlations for y and z components (not shown) can be generated by ±120° rotations of the images shown.
obtained by exact diagonalization using a 24-site cluster and plotted in the extended Brillouin zone for selected ξ. The correlations for y and z components (not shown) can be generated by ±120° rotations of the images shown.
Interpreted within this model, our calculations would imply that the system is very close to the Kitaev limit. However, it is becoming increasingly evident that other anisotropic terms beyond the Kitaev interaction do play a role22,23. This is, in fact, evident from the static spin not pointing along one of the cubic axes favoured by the K term; all other anisotropic terms conspire to rotate the spin away from the principal axes. This in turn suggests that the zigzag structure is further stabilized by other anisotropic terms. The zigzag correlations survive at least up to ∼70 K (see Supplementary Fig. 3), which is in accord with the observation that coherent spin waves15 disperse up to ≍5 meV. This energy scale coincides with the temperature scale (≍100 K) below which the magnetic susceptibility deviates from the Curie–Weiss behaviour33. This energy scale is, however, still far too small in comparison with the energy (≍100 meV) spanned by the magnetic excitations (Fig. 4), suggesting that the zigzag order is an emergent phenomenon. Despite the macroscopic degeneracy in the Kitaev QSL phase being reduced down to three zigzags, the high-energy Kitaev interactions leave their signature in the low-energy sector: the three spin components, each carrying its own zigzag, compete and melt the long-range order at a temperature much lower than that suggested by the Weiss temperature (ΘW), leading to a large frustration parameter33 (≡ΘW/TN) approximately equal to 8.
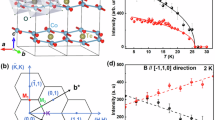
RIXS spectra recorded at T = 9 K and Ψ = 180°.Q = (0, 1), (0.5, 0.5) and (0.5, −0.5), shown as blue, green and yellow filled symbols, respectively, marked on the Brillouin zone of the honeycomb net and colour-coded with the spectra. At this Ψ angle, S lies approximately along kf and π–σ′ and π–π′ channels measure the two spin components transverse to S. For comparison, the inset shows the diffuse map at T = 17 K for the same Ψ angle, generated by rotating the Ψ = 60° data shown in Fig. 2a clockwise by 120°.
The fluctuations among three zigzag states remain even below TN, albeit with subtle spectral changes (Supplementary Fig. 3d), implying that they are primarily quantum rather than thermal fluctuations. At Ψ = 180° (Fig. 4), the intensity remains highest at Q = ±(0.5, 0.5) and Q = ±(0.5, −0.5), away from the Bragg peaks at Q = ±(0, 1), and peaked at zero energy within the energy resolution of 24 meV. Note that this scattering geometry probes two spin components transverse to the static component. A profound consequence of the unusual nature of the fluctuations is that the soft excitations are located away from the Bragg peak15. This is a notable exception to the universality held in conventional magnets that spin waves emanate from Bragg peaks by virtue of the Goldstone theorem, and magnetic anisotropy is manifested as a spin-wave gap, even in systems with extremely large magnetic anisotropy34. By contrast, the spin gap in our system is small (unresolved in our spectra and estimated to be smaller than 2 meV from INS data15) in comparison with the overall energy scale of the system, despite the fact that the magnetism is dominated by the anisotropic terms. Rather, the anisotropy is manifested as the separation of the long-wavelength spin waves from the Bragg peaks, which is a natural consequence of each spin component exhibiting its own real-space correlations. Our results directly reveal the key building blocks of the Kitaev model in Na2IrO3, and establish a new design strategy for the long-sought quantum spin liquids via the bond-directional magnetic coupling.
Methods
Single-crystal growth.
Single crystals of Na2IrO3 were grown following two different recipes using Na2CO3 flux (Sample 1) and self-flux (Sample 2). For Sample 1, a mixture of Na2CO3 and IrO2 with a molar ratio of 50:1 was melted at 1,050 °C for 6 h followed by fast cooling at a rate of 100 °C h−1 down to 1,000 °C, slow cooling at a rate of 1 °C h−1 down to 800 °C and furnace cooling to room temperature in sequence. Hexagonal pillar-shaped crystals with typical dimensions of 0.2 mm × 0.2 mm × 0.4 mm were obtained after dissolving Na2CO3 flux in acetone and water. For Sample 2, powders of Na2CO3 were mixed with 10–20% excess IrO2 and were calcined at 700 °C for 24 h. Single crystals were grown on top of a powder matrix in a subsequent heating at 1,050 °C. Plate-like crystals with typical dimensions of 5 mm × 5 mm × 0.1 mm were physically extracted.
Resonant X-ray scattering.
Incident X-rays were tuned to the Ir L3 edge (11.2145 keV). The resonant X-ray diffraction experiments were carried out at the 6 ID-B beamline of the Advanced Photon Source. The polarization analysis was performed in the vertical scattering geometry using a pyrolytic graphite analyser probing the σ–π′ channel. The RIXS was performed at ID20 of the European Synchrotron Radiation Facility. The total instrumental energy resolution of 24 meV was achieved with a monochromator and a diced spherical analyser made from Si (844) and a position-sensitive area detector placed on a Rowland circle with a 2 m radius. The diffuse magnetic scattering was performed using the RIXS spectrometers at the 9 ID, 27 ID and 30 ID (MERIX) beamlines of the Advanced Photon Source, where a monochromator of 90 meV bandwidth was used for an order-of-magnitude higher incident photon flux than that from the Si (844) monochromator. In these experiments, a horizontal scattering geometry was used with the π-incident X-ray polarization measuring the sum of π–σ′ and π–π′ channels. The 2θ angle was fixed at 90° to minimize the contribution from Thompson elastic scattering. As a result, L values in the HK maps shown in Fig. 2a vary in the range between 6.5 and 7. The in-plane momentum resolution of the RIXS spectrometer was ±0.048 Å−1. The use of RIXS spectrometers rejecting all inelastically scattered X-rays outside of the 100 meV energy window centred at the elastic line led to a significant improvement in the signal-to-noise ratio. A typical counting time of 2 h was required for a map shown inFig. 2.
References
van Vleck, J. H. On the anisotropy of cubic ferromagnetic crystals. Phys. Rev. 52, 1178–1198 (1937).
Khaliullin, G. Orbital order and fluctuations in Mott insulators. Prog. Theor. Phys. Suppl. 160, 155–202 (2005).
Jackeli, G. & Khaliullin, G. Mott insulators in the strong spin–orbit coupling limit: From Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009).
Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006).
Kim, B. J. et al. Novel Jeff = 1/2 Mott state induced by relativistic spin–orbit coupling in Sr2IrO4 . Phys. Rev. Lett. 101, 076402 (2008).
Kim, B. J. et al. Phase-sensitive observation of a spin–orbital Mott state in Sr2IrO4 . Science 323, 1329–1332 (2009).
Takayama, T. et al. Hyper-honeycomb iridate β-Li2IrO3 as a platform for Kitaev magnetism. Phys. Rev. Lett. 114, 077202 (2015).
Modic, K. A. et al. Realization of a three-dimensional spin-anisotropic harmonic honeycomb iridate. Nature Commun. 5, 4203 (2014).
Kimchi, I. & Vishwanath, A. Kitaev–Heisenberg models for iridates on the triangular, hyperkagome, kagome, fcc, and pyrochlore lattices. Phys. Rev. B 89, 014414 (2014).
Hermanns, M. & Trebst, S. Quantum spin liquid with a Majorana Fermi surface on the three-dimensional hyperoctagon lattice. Phys. Rev. B 89, 235102 (2014).
Lee, S. B., Jeong, J-S., Hwang, K. & Kim, Y. B. Emergent quantum phases in a frustrated J1–J2 Heisenberg model on the hyperhoneycomb lattice. Phys. Rev. B 90, 134425 (2014).
Plumb, K. W. et al. α-RuCl3: A spin–orbit assisted Mott insulator on a honeycomb lattice. Phys. Rev. B 90, 041112 (2014).
Luo, Y. et al. Li2RhO3: A spin-glassy relativistic Mott insulator. Phys. Rev. B 87, 161121 (2013).
Liu, X. et al. Long-range magnetic ordering in Na2IrO3 . Phys. Rev. B 83, 220403 (2011).
Choi, S. K. et al. Spin waves and revised crystal structure of honeycomb iridate Na2IrO3 . Phys. Rev. Lett. 108, 127204 (2012).
Ye, F. et al. Direct evidence of a zigzag spin-chain structure in the honeycomb lattice: A neutron and X-ray diffraction investigation of single-crystal Na2IrO3 . Phys. Rev. B 85, 180403 (2012).
Reuther, J., Thomale, R. & Rachel, S. Spiral order in the honeycomb iridate Li2IrO3 . Phys. Rev. B 90, 100405 (2014).
Biffin, A. et al. Noncoplanar and counterrotating incommensurate magnetic order stabilized by Kitaev interactions in γ-Li2IrO3 . Phys. Rev. Lett. 113, 197201 (2014).
Biffin, A. et al. Unconventional magnetic order on the hyperhoneycomb Kitaev lattice in β-Li2IrO3: Full solution via magnetic resonant X-ray diffraction. Phys. Rev. B 90, 205116 (2014).
Chaloupka, J., Jackeli, G. & Khaliullin, G. Kitaev–Heisenberg model on a honeycomb lattice: Possible exotic phases in iridium oxides A2IrO3 . Phys. Rev. Lett. 105, 027204 (2010).
Chaloupka, J., Jackeli, G. & Khaliullin, G. Zigzag magnetic order in the iridium oxide Na2IrO3 . Phys. Rev. Lett. 110, 097204 (2013).
Lee, E. K-H. & Kim, Y. B. Theory of magnetic phase diagrams in hyperhoneycomb and harmonic-honeycomb iridates. Phys. Rev. B 91, 064407 (2015).
Rau, J. G., Lee, E. K-H. & Kee, H-Y. Generic spin model for the honeycomb iridates beyond the Kitaev limit. Phys. Rev. Lett. 112, 077204 (2014).
Katukuri, V. M. et al. Kitaev interactions between j = 1/2 moments in honeycomb Na2IrO3 are large and ferromagnetic: Insights from ab initio quantum chemistry calculations. New J. Phys. 16, 013056 (2014).
Yamaji, Y., Nomura, Y., Kurita, M., Arita, R. & Imada, M. First-principles study of the honeycomb-lattice iridates Na2IrO3 in the presence of strong spin–orbit interaction and electron correlations. Phys. Rev. Lett. 113, 107201 (2014).
Shitade, A. et al. Quantum spin Hall effect in a transition metal oxide Na2IrO3 . Phys. Rev. Lett. 102, 256403 (2009).
Mazin, I. I., Jeschke, H. O., Foyevtsova, K., Valenti, R. & Khomskii, D. I. Na2IrO3 as a molecular orbital crystal. Phys. Rev. Lett. 109, 197201 (2012).
Kim, C. H., Kim, H. S., Jeong, H., Jin, H. & Yu, J. Topological quantum phase transition in 5d transition metal oxide Na2IrO3 . Phys. Rev. Lett. 108, 106401 (2012).
Gretarsson, H. et al. Magnetic excitation spectrum of Na2IrO3 probed with resonant inelastic X-ray scattering. Phys. Rev. B 87, 220407 (2013).
Price, C. & Perkins, N. B. Finite-temperature phase diagram of the classical Kitaev–Heisenberg model. Phys. Rev. B 88, 024410 (2013).
Fujiyama, S. et al. Two-dimensional Heisenberg behavior of Jeff = 1/2 isospins in the paramagnetic state of the spin–orbital Mott insulator Sr2IrO4 . Phys. Rev. Lett. 108, 247212 (2012).
Kimchi, I. & You, Y-Z. Kitaev–Heisenberg-J2-J3 model for the iridates A2IrO3 . Phys. Rev. B 84, 180407 (2011).
Singh, Y. & Gegenwart, P. Antiferromagnetic Mott insulating state in single crystals of the honeycomb lattice material Na2IrO3 . Phys. Rev. B 82, 064412 (2010).
Kim, J. et al. Large spin-wave energy gap in the bilayer iridate Sr3Ir2O7: Evidence for enhanced dipolar interactions near the Mott metal–insulator transition. Phys. Rev. Lett. 109, 157402 (2012).
Acknowledgements
Work in the Materials Science Division of Argonne National Laboratory (sample preparation, characterization, and contributions to data analysis) was supported by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Science and Engineering Division. Use of the Advanced Photon Source, an Office of Science User Facility operated for the US Department of Energy (DOE) Office of Science by Argonne National Laboratory, was supported by the US DOE under Contract No. DE-AC02-06CH11357. K.M. acknowledges support from UGC-CSIR, India. Y.S. acknowledges DST, India for support through Ramanujan Grant #SR/S2/RJN-76/2010 and through DST grant #SB/S2/CMP-001/2013. J.C. was supported by ERDF under project CEITEC (CZ.1.05/1.1.00/02.0068) and EC 7th Framework Programme (286154/SYLICA).
Author information
Authors and Affiliations
Contributions
B.J.K. conceived the project. S.H.C., J-W.K., J.K. and B.J.K. performed the experiment with support from Y.C., T.G., A.A-Z., M.M.S. and M.K. H.Z. and K.M. grew the single crystals; C.C.S., C.D.M. and K.M. characterized the samples under the supervision of J.F.M. and Y.S. S.H.C., J-W.K. and B.J.K. analysed the data. J.C. performed the numerical calculations. J.C., G.J. and G.K. developed the theoretical model. All authors discussed the results. B.J.K. led the manuscript preparation with contributions from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 585 kb)
Rights and permissions
About this article
Cite this article
Hwan Chun, S., Kim, JW., Kim, J. et al. Direct evidence for dominant bond-directional interactions in a honeycomb lattice iridate Na2IrO3. Nature Phys 11, 462–466 (2015). https://doi.org/10.1038/nphys3322
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3322
This article is cited by
-
Kitaev spin-orbital bilayers and their moiré superlattices
npj Quantum Materials (2023)
-
A magnetic continuum in the cobalt-based honeycomb magnet BaCo2(AsO4)2
Nature Materials (2023)
-
Theory of the Kitaev model in a [111] magnetic field
Nature Communications (2022)
-
Giant stress response of terahertz magnons in a spin-orbit Mott insulator
Nature Communications (2022)
-
Proximate ferromagnetic state in the Kitaev model material α-RuCl3
Nature Communications (2021)