Abstract
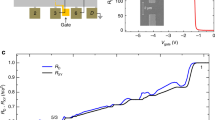
The fractional quantum Hall (FQH) effect emerges in high-quality two-dimensional electron systems exposed to a magnetic field when the Landau-level filling factor, νe, takes on a rational value. Although the overwhelming majority of FQH states have odd-denominator fillings, the physical properties of the rare and fragile even-denominator states are most tantalizing in view of their potential relevance for topological quantum computation. For decades, GaAs has been the preferred host for studying these even-denominator states, where they occur at νe = 5/2 and 7/2. Here we report an anomalous series of quantized even-denominator FQH states outside the realm of III–V semiconductors in the MgZnO/ZnO 2DES electron at νe = 3/2 and 7/2, with precursor features at 9/2; all while the 5/2 state is absent. The effect in this material occurs concomitantly with tunability of the orbital character of electrons at the chemical potential, thereby realizing a new experimental means for investigating these exotic ground states.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Das Sarma, S. & Pinczuk, A. (eds) Perspectives in the Quantum Hall Effects (John Wiley, 1997).
Suen, Y. W., Engel, L. W., Santos, M. B., Shayegan, M. & Tsui, D. C. Observation of a ν = 1/2 fractional quantum Hall state in a double-layer electron system. Phys. Rev. Lett. 68, 1379–1382 (1992).
Eisenstein, J. P., Boebinger, G. S., Pfeiffer, L. N., West, K. W. & Song, H. New fractional quantum Hall state in double-layer two-dimensional electron systems. Phys. Rev. Lett. 68, 1383–1386 (1992).
Luhman, D. et al. Observation of a fractional quantum Hall state at ν = 1/4 in a wide GaAs quantum well. Phys. Rev. Lett. 101, 266804 (2008).
Liu, Y. et al. Fractional quantum Hall effect at ν = 1/2 in hole systems confined to GaAs quantum wells. Phys. Rev. Lett. 112, 046804 (2014).
Liu, Y. et al. Even-denominator fractional quantum Hall effect at a Landau level crossing. Phys. Rev. B 89, 165313 (2014).
Wiedmann, S., Gusev, G. M., Bakarov, A. K. & Portal, J. C. Emergent fractional quantum Hall effect at even denominator ν = 3/2 in a triple quantum well in tilted magnetic fields. J. Phys. Conf. Ser. 334, 012026 (2011).
Ki, D-K., Fal’ko, V., Abanin, D. A. & Morpurgo, A. Observation of even-denominator fractional quantum Hall effect in suspended bilayer graphene. Nano Lett. 14, 2135–2139 (2014).
Willett, R. et al. Observation of an even-denominator quantum number in the fractional quantum Hall effect. Phys. Rev. Lett. 59, 1776–1779 (1987).
Pan, W. et al. Exact quantization of the even-denominator fractional quantum Hall state at ν = 5/2 Landau level filling factor. Phys. Rev. Lett. 83, 3530–3533 (1999).
Eisenstein, J. P., Cooper, K. B., Pfeiffer, L. N. & West, K. W. Insulating and fractional quantum Hall states in the first excited Landau level. Phys. Rev. Lett. 88, 076801 (2002).
Halperin, B. I. Theory of the quantized Hall conductance. Helv. Phys. Acta 56, 75–102 (1983).
Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989).
Scarola, V. W., Park, K. & Jain, J. K. Cooper instability of composite fermions. Nature 406, 863–865 (2000).
Moore, G. & Read, N. Nonabelions in the fractional quantum Hall effect. Nucl. Phys. B 360, 362–396 (1991).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Stern, A. Non-Abelian states of matter. Nature 464, 187–193 (2010).
Lilly, M. P., Cooper, K. B., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Evidence for an anisotropic state of two-dimensional electrons in high Landau levels. Phys. Rev. Lett. 82, 394–397 (1999).
Fogler, M. M. & Koulakov, A. A. Laughlin liquid to charge-density-wave transition at high Landau levels. Phys. Rev. B 55, 9326–9329 (1997).
Rezayi, E. H., Haldane, F. D. M. & Yang, K. Charge-density-wave ordering in half-filled high Landau levels. Phys. Rev. Lett. 83, 1219–1222 (1999).
Tsukazaki, A. et al. Observation of the fractional quantum Hall effect in an oxide. Nature Mater. 9, 889–893 (2010).
Vakili, K. et al. Spin-dependent resistivity at transitions between integer quantum Hall states. Phys. Rev. Lett. 94, 176402 (2005).
Gamez, G. & Muraki, K. ν = 5/2 fractional quantum Hall state in low-mobility electron systems: Different roles of disorder. Phys. Rev. B 88, 075308 (2013).
De Poortere, E. P., Tutuc, E., Papadakis, S. J. & Shayegan, M. Resistance spikes at transitions between quantum Hall ferromagnets. Science 290, 1546–1549 (2000).
Jungwirth, T. & MacDonald, A. H. Resistance spikes and domain wall loops in Ising quantum ferromagnets. Phys. Rev. Lett. 87, 216801 (2001).
MacDonald, A. H. & Girvin, S. M. Collective excitations of fractional Hall states and Wigner crystallization in higher Landau levels. Phys. Rev. B 33, 4009–4013 (1986).
Choi, H. C., Kang, W., Das Sarma, S., Pfeiffer, L. N. & West, K. W. Activation gaps of fractional quantum Hall effect in the second Landau level. Phys. Rev. B 77, 081301 (2008).
Du, R. R. et al. Fractional quantum Hall effect around ν = 3/2: Composite fermions with a spin. Phys. Rev. Lett. 75, 3926–3929 (1995).
Pan, W. et al. Strongly anisotropic electronic transport at Landau level filling factor ν = 9/2 and ν = 5/2 under a tilted magnetic field. Phys. Rev. Lett. 83, 820–823 (1999).
Lilly, M. P., Cooper, K. B., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Anisotropic states of two-dimensional electron systems in high Landau levels: Effect of an in-plane magnetic field. Phys. Rev. Lett. 83, 824–827 (1999).
Sodemann, I. & MacDonald, A. H. Theory of native orientational pinning in quantum Hall nematics. Preprint at http://arXiv.org/abs/1307.5489 (2013).
Papić, Z. & Abanin, D. A. Topological phases in the zeroth Landau level of bilayer graphene. Phys. Rev. Lett. 112, 046602 (2014).
Falson, J., Maryenko, D., Kozuka, Y., Tsukazaki, A. & Kawasaki, M. Magnesium doping controlled density and mobility of two-dimensional electron gas in MgxZn1−xO/ZnO heterostructures. Appl. Phys. Express 4, 091101 (2011).
Acknowledgements
We thank K. v. Klitzing, T. Arima, R. Morf, M. Shayegan, Y. Liu and V. Scarola for discussions. This work was partly supported by Grant-in-Aids for Scientific Research (S) No. 24226002 from MEXT, Japan, ‘Funding Program for World-Leading Innovative R&D on Science and Technology (FIRST)’ Program from the Japan Society for the Promotion of Science (JSPS) initiated by the Council for Science and Technology Policy and the German Ministry of Science and Education (BMBF). J.F. acknowledges the support of the Marubun Research Promotion Foundation.
Author information
Authors and Affiliations
Contributions
J.F. grew the heterostructure. J.F., B.F. and D.Z. performed the low-temperature measurements. J.F. analysed the data. J.F. and J.H.S. wrote the manuscript with input from all authors. All authors discussed the results and planned the experiments with J.F., D.M., Y.K., A.T. and M.K. initiating the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 7933 kb)
Rights and permissions
About this article
Cite this article
Falson, J., Maryenko, D., Friess, B. et al. Even-denominator fractional quantum Hall physics in ZnO. Nature Phys 11, 347–351 (2015). https://doi.org/10.1038/nphys3259
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3259
This article is cited by
-
Electronic Structure of a Wide Quantum Wire in a Magnetic Field at ν = 1
International Journal of Theoretical Physics (2024)
-
Size dependence- and induced transformations- of fractional quantum Hall effects under tilted magnetic fields
Scientific Reports (2022)
-
Competing correlated states around the zero-field Wigner crystallization transition of electrons in two dimensions
Nature Materials (2022)
-
Ultra-high-quality two-dimensional electron systems
Nature Materials (2021)
-
Odd- and even-denominator fractional quantum Hall states in monolayer WSe2
Nature Nanotechnology (2020)