Abstract
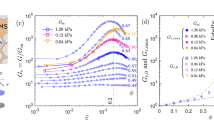
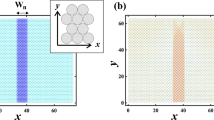
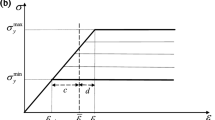
From bone and wood to concrete and carbon fibre, composites are ubiquitous natural and synthetic materials. Eshelby’s inclusion theory describes how macroscopic stress fields couple to isolated microscopic inclusions, allowing prediction of a composite’s bulk mechanical properties from a knowledge of its microstructure. It has been extended to describe a wide variety of phenomena from solid fracture to cell adhesion. Here, we show experimentally and theoretically that Eshelby’s theory breaks down for small liquid inclusions in a soft solid. In this limit, an isolated droplet’s deformation is strongly size-dependent, with the smallest droplets mimicking the behaviour of solid inclusions. Furthermore, in opposition to the predictions of conventional composite theory, we find that finite concentrations of small liquid inclusions enhance the stiffness of soft solids. A straightforward extension of Eshelby’s theory, accounting for the surface tension of the solid–liquid interface, explains our experimental observations. The counterintuitive stiffening of solids by fluid inclusions is expected whenever inclusion radii are smaller than an elastocapillary length, given by the ratio of the surface tension to Young’s modulus of the solid matrix. These results suggest that surface tension can be a simple and effective mechanism to cloak the far-field elastic signature of inclusions.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Change history
08 January 2015
In the text following equation 7, the expression describing the limit where stiffening occurs was incorrect and should have read: surface tension dominates over elasticity (R « ϒ /E ). This has now been corrected in the online versions of the Article.
References
Ashby, M. F. Overview no. 80: On the engineering properties of materials. Acta Metall. 37, 1273–1293 (1989).
Höhler, R. & Cohen-Addad, S. Rheology of liquid foam. J. Phys. Condens. Matter 17, R1041 (2005).
Eshelby, J. D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. A 241, 376–396 (1957).
Hashin, Z. & Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 11, 127–140 (1963).
Mori, T. & Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 21, 571–574 (1973).
Rice, J. R. A path independent integral and the approximate analysis of strain concentration by notches and cracks. J. Appl. Mech. 35, 379–386 (1968).
Budiansky, B. & O’Connell, R. J. Elastic moduli of a cracked solid. Int. J. Solids Struct. 12, 81–97 (1976).
Hutchinson, J. Elastic-plastic behaviour of polycrystalline metals and composites. Proc. R. Soc. Lond. A 319, 247–272 (1970).
Berveiller, M. & Zaoui, A. An extension of the self-consistent scheme to plastically-flowing polycrystals. J. Mech. Phys. Solids 26, 325–344 (1978).
Jensen, K. E., Weitz, D. A. & Spaepen, F. Local shear transformations in deformed and quiescent hard-sphere colloidal glasses. Phys. Rev. E 90, 042305 (2014).
Zemel, A., Rehfeldt, F., Brown, A. E. X., Discher, D. E. & Safran, S. A. Optimal matrix rigidity for stress-fibre polarization in stem cells. Nature Phys. 6, 468–473 (2010).
Schwarz, U. S. & Safran, S. A. Physics of adherent cells. Rev. Mod. Phys. 85, 1327–1381 (2013).
Gurtin, M. E. & Murdoch, A. I. A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 57, 291–323 (1975).
Palierne, J. F. Linear rheology of viscoelastic emulsions with interfacial tension. Rheol. Acta 29, 204–214 (1990).
Brisard, S., Dormieux, L. & Kondo, D. Hashin–Shtrikman bounds on the shear modulus of a nanocomposite with spherical inclusions and interface effects. Comput. Mater. Sci. 50, 403–410 (2010).
Shuttleworth, R. The surface tension of solids. Proc. Phys. Soc. A 63, 444–457 (1950).
Hui, C-Y. & Jagota, A. Surface tension, surface energy, and chemical potential due to their difference. Langmuir 29, 11310–11316 (2013).
Needham, D. & Hochmuth, R. A sensitive measure of surface stress in the resting neutrophil. Biophys. J. 61, 1664–1670 (1992).
Lecuit, T. & Lenne, P-F. Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nature Rev. Mol. Cell Biol. 8, 633–644 (2007).
Mora, S. et al. Solid drops: Large capillary deformations of immersed elastic rods. Phys. Rev. Lett. 111, 114301 (2013).
Style, R. W. & Dufresne, E. R. Static wetting on deformable substrates, from liquids to soft solids. Soft Matter 8, 7177–7184 (2012).
Style, R. W., Che, Y., Wettlaufer, J. S., Wilen, L. A. & Dufresne, E. R. Universal deformation of soft substrates near a contact line and the direct measurement of solid surface stresses. Phys. Rev. Lett. 110, 066103 (2013).
Style, R. W. et al. Patterning droplets with durotaxis. Proc. Natl Acad. Sci. USA 110, 12541–12544 (2013).
Nadermann, N., Hui, C-Y. & Jagota, A. Solid surface tension measured by a liquid drop under a solid film. Proc. Natl Acad. Sci. USA 110, 10541–10545 (2013).
Karpitschka, S., Das, S., Andreotti, B. & Snoeijer, J. Dynamic contact angle of a soft solid. Preprint at http://arXiv.org/abs/1406.5547v1 (2014).
Bostwick, J. B., Shearer, M. & Daniels, K. E. Elastocapillary deformations on partially-wetting substrates: Rival contact-line models. Soft Matter 10, 7361–7369 (2014).
Style, R. W., Hyland, C., Boltyanskiy, R., Wettlaufer, J. S. & Dufresne, E. R. Surface tension and contact with soft elastic solids. Nature Commun. 4, 2728 (2013).
Salez, T., Benzaquen, M. & Raphael, E. From adhesion to wetting of a soft particle. Soft Matter 9, 10699–10704 (2013).
Xu, X., Jagota, A. & Hui, C-Y. Effects of surface tension on the adhesive contact of a rigid sphere to a compliant substrate. Soft Matter 10, 4625–4632 (2014).
Cao, Z., Stevens, M. J. & Dobrynin, A. V. Adhesion and wetting of nanoparticles on soft surfaces. Macromolecules 47, 3203–3209 (2014).
Mora, S., Phou, T., Fromental, J-M., Pismen, L. M. & Pomeau, Y. Capillarity driven instability of a soft solid. Phys. Rev. Lett. 105, 214301 (2010).
Chen, D., Cai, S., Suo, Z. & Hayward, R. C. Surface energy as a barrier to creasing of elastomer films: An elastic analogy to classical nucleation. Phys. Rev. Lett. 109, 038001 (2012).
Yang, F. Size-dependent effective modulus of elastic composite materials: Spherical nanocavities at dilute concentrations. J. Appl. Phys. 95, 3516–3520 (2004).
Sharma, P. & Ganti, S. Size-dependent eshelbyõs tensor for embedded nano-inclusions incorporating surface/interface energies. J. Appl. Mech. 71, 663–671 (2004).
Ducloue, L., Pitois, O., Goyon, J., Chateau, X. & Ovarlez, G. Coupling of elasticity to capillarity in soft aerated materials. Soft Matter 10, 5093–5098 (2014).
Cox, R. G. The deformation of a drop in a general time-dependent fluid flow. J. Fluid Mech. 37, 601–623 (1969).
Chakrabarti, A. & Chaudhury, M. K. Direct measurement of the surface tension of a soft elastic hydrogel: Exploration of elastocapillary instability in adhesion. Langmuir 29, 6926–6935 (2013).
Style, R. W., Wettlaufer, J. S. & Dufresne, E. R. Surface tension and the mechanics of liquid inclusions in compliant solids. Soft Matter (in the press). Preprint at http://arXiv.org/abs/1409.1998 (2014).
Duan, H. L., Wang, J., Huang, Z. P. & Karihaloo, B. L. Eshelby formalism for nano-inhomogeneities. Proc. R. Soc. A 461, 3335–3353 (2005).
Wang, J., Duan, H., Huang, Z. & Karihaloo, B. A scaling law for properties of nano-structured materials. Proc. R. Soc. A 462, 1355–1363 (2006).
Park, S. J. et al. Visualization of asymmetric wetting ridges on soft solids with X-ray microscopy. Nature Commun. 5, 4369 (2014).
Duan, H. L., Yi, X., Huang, Z. P. & Wang, J. A unified scheme for prediction of effective moduli of multiphase composites with interface effects. part i: Theoretical framework. Mech. Mater. 39, 81–93 (2007).
Milton, G. W., Briane, M. & Willis, J. R. On cloaking for elasticity and physical equations with a transformation invariant form. New J. Phys. 8, 248 (2006).
Bückmann, T., Thiel, M., Kadic, M., Schittny, R. & Wegener, M. An elasto-mechanical unfeelability cloak made of pentamode metamaterials. Nature Commun. 5, 4130 (2014).
Dickinson, E. Emulsion gels: The structuring of soft solids with protein-stabilized oil droplets. Food Hydrocolloids 28, 224–241 (2012).
Hill, R. A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 13, 213–222 (1965).
Brisard, S., Dormieux, L. & Kondo, D. Hashin–Shtrikman bounds on the bulk modulus of a nanocomposite with spherical inclusions and interface effects. Comput. Mater. Sci. 48, 589–596 (2010).
Brown, R., Prajapati, R., McGrouther, D., Yannas, I. & Eastwood, M. Tensional homeostasis in dermal fibroblasts: Mechanical responses to mechanical loading in three-dimensional substrates. J. Cell. Physiol. 175, 323–332 (1998).
Zemel, A., Bischofs, I. & Safran, S. Active elasticity of gels with contractile cells. Phys. Rev. Lett. 97, 128103 (2006).
Campàs, O. et al. Quantifying cell-generated mechanical forces within living embryonic tissues. Nature Methods 11, 183–189 (2014).
Acknowledgements
We thank J. Fernandez-Garcia for the ionic liquids, and T. Kodger and R. Diebold for advice in preparing silicone. We also thank J. Singer, M. Rooks, F. Spaepen, S. Mukhopadhyay, P. Howell and A. Goriely for helpful conversations. We gratefully acknowledge funding from the National Science Foundation (CBET-1236086) to E.R.D., the Yale University Bateman Interdepartmental Postdoctoral Fellowship to R.W.S., and the John Simon Guggenheim Foundation, the Swedish Research Council and a Royal Society Wolfson Research Merit Award to J.S.W.
Author information
Authors and Affiliations
Contributions
R.W.S., R.B., B.A., K.E.J., H.P.F. and E.R.D. designed experiments. R.W.S., B.A. and R.B. acquired data. R.W.S. and E.R.D. analysed data. R.W.S., J.S.W. and E.R.D. developed the theory. R.W.S., J.S.W. and E.R.D. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 1306 kb)
Rights and permissions
About this article
Cite this article
Style, R., Boltyanskiy, R., Allen, B. et al. Stiffening solids with liquid inclusions. Nature Phys 11, 82–87 (2015). https://doi.org/10.1038/nphys3181
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3181
This article is cited by
-
Elastic microphase separation produces robust bicontinuous materials
Nature Materials (2024)
-
A liquid inclusion having an n-fold axis of symmetry in an infinite isotropic elastic matrix
Continuum Mechanics and Thermodynamics (2024)
-
Green’s functions for an anisotropic elastic matrix containing an elliptical incompressible liquid inclusion
Zeitschrift für angewandte Mathematik und Physik (2024)
-
Temperature Dependence of Elastic Properties of Al-Mg-Si Direct-Chill-Cast AA6111 Alloy at Near-Solidus Temperatures
Journal of Materials Engineering and Performance (2024)
-
Vascular smooth muscle-inspired architecture enables soft yet tough self-healing materials for durable capacitive strain-sensor
Nature Communications (2023)