Abstract
Sixty years ago, Karplus and Luttinger pointed out that quantum particles moving on a lattice could acquire an anomalous transverse velocity in response to a force, providing an explanation for the unusual Hall effect in ferromagnetic metals1. A striking manifestation of this transverse transport was then revealed in the quantum Hall effect2 where the plateaux depicted by the Hall conductivity were attributed to a topological invariant characterizing the Bloch bands: the Chern number3. Until now, topological transport associated with non-zero Chern numbers has only been observed in electronic systems2,4,5. Here we use the transverse deflection of an atomic cloud in response to an optical gradient to measure the Chern number of artificially generated Hofstadter bands6. These topological bands are very flat and thus constitute good candidates for the realization of fractional Chern insulators7. Combining these deflection measurements with the determination of the band populations, we obtain an experimental value for the Chern number of the lowest band νexp = 0.99(5). This first Chern-number measurement in a non-electronic system is facilitated by an all-optical artificial gauge field scheme, generating uniform flux in optical superlattices.
Similar content being viewed by others
Main
One of the most challenging goals in the context of artificial gauge fields is to implement experimental probes revealing the non-trivial topology of energy bands. This would open the path towards the realization of novel topological states of matter in a wide class of physical settings, ranging from cold atoms to polariton gases8,9,10,11. Considering cold atoms in optical lattices, it has been shown theoretically that transport measurements could allow a determination of the Chern number characterizing topological Bloch bands8,12,13. Although earlier experiments used local cyclotron orbits to detect the artificial gauge field structure at the single-plaquette level14,15, observing the entire cloud dynamics or determining the Chern number of the underlying bands has remained out of reach. Here we load ultracold bosonic atoms into Hofstadter bands, and we report on the direct detection of the cloud’s spatial motion as a response to an applied force. Using a novel band-mapping technique, we track the populations of the Hofstadter bands over time. We observe that the flatness of the bands leads to homogeneous populations within individual bands, through interactions and finite temperatures. For short times, heating and non-adiabatic interaction effects are limited, and the detected transverse Hall drift is in agreement with exact diagonalization studies12,13. Combined with independent band-population measurements, we extract the Chern number of the lowest Hofstadter band from our experimental data. Our work represents the first determination of a topological invariant characterizing two-dimensional Bloch bands using ultracold atoms, and complements other studies based on atom interferometric16,17 and collective-mode18 measurements.
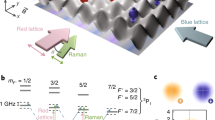
Our optical-lattice set-up realizes the celebrated Harper–Hofstadter Hamiltonian6, which describes the motion of particles on a square lattice penetrated by a uniform magnetic flux Φ per unit cell (see also the original works by Harper19 and Azbel20). An atom that hops around a closed loop of the optical lattice picks up a geometric phase, which mimics the Aharonov–Bohm phase of a charged particle in a magnetic field. The artificial flux is thus produced by engineering complex tunnelling matrix elements with space-dependent (Peierls) phases6, through the laser-assisted-tunnelling method introduced by Jaksch and Zoller21 and subsequent works9,22,23,24,25. The present scheme controls tunnelling along the x direction and uses two main ingredients: a staggered potential with energy offset Δ between neighbouring sites, inhibiting bare tunnelling along x, together with a resonant modulation of frequency ω = Δ/ℏ, restoring the hopping in a controlled way. Using a simple time-dependent optical potential, which simultaneously triggers the hopping on all the links, naturally produces a staggered flux distribution14. To rectify the flux, we implement a new all-optical driving scheme that uses two pairs of laser beams to control the laser-induced tunnelling on successive links independently, hence producing a uniform flux Φ = π/2 per unit cell (Fig. 1a). The lowest band of the corresponding energy spectrum has a Chern number ν1 = +1 and is thus topologically equivalent to the lowest Landau level. Moreover, this band exhibits a large flatness ratio of Egap/Ebw ≃ 7, where Egap is the energy gap to the second band and Ebw the bandwidth. In contrast to previous experiments generating uniform flux in optical lattices15,26, the present scheme does not rely on magnetic field gradients, and therefore offers a higher degree of experimental control.
a, The set-up consists of a two-dimensional optical lattice with lattice constant a = λs/2 and tunnel couplings Jx, Jy between neighbouring sites. Bare tunnelling is inhibited along x by a staggered potential, creating an offset Δ between grey and white sites. Two further pairs of laser beams (red and blue arrows), with wavevectors |kij| ≃ kL = π/(2a) (i = {r, b} and j = {1,2}) and resonant frequency difference ωi = ωi2 − ωi1 = ±Δ/ℏ, are used to restore tunnelling. Each pair consists of two beams, one running-wave (along y) and one retro-reflected beam (along x, arrows with lighter shading). Tunnelling on red and blue links is controlled independently by the i = r and i = b beams, respectively, hence generating a rectified flux Φ = π/2 per plaquette (aligned along −êz). The magnetic unit cell (grey shaded area) is four times larger than the usual lattice unit cell. b, The Chern number is extracted from the transverse displacement of the atomic cloud in response to an external force generated by an optical gradient.
The experimental set-up consists of an ultracold gas of 87Rb atoms that is loaded into a two-dimensional lattice created by two orthogonal standing waves with wavelength λs = 767 nm. The atoms are confined in the perpendicular direction by a weak harmonic potential using an optical dipole trap. A further standing wave with twice the wavelength λL = 2λs is superimposed along x to create the staggered potential (Fig. 1a), with an energy offset Δ much larger than the bare tunnelling Jx. The modulation restoring resonant tunnelling is created by two further pairs of far-detuned laser beams, each pair generating a moving potential of the form Vi(x, y, t) = κ cos(kLx + φi)cos(−kLy ± ωt), where κ is the driving amplitude, kL = 2π/λL, and ω = Δ/ℏ. The relative phases φi are adjusted so as to control successive links independently (Fig. 1a). In the high-frequency limit ℏω ≫ Jx, Jy, this system can be described by an effective time-independent Hamiltonian27,28,29,30,31, whose dominant contributions reproduce the Harper–Hofstadter Hamiltonian (Methods)

where the Landau gauge was chosen to describe the system6. Here  annihilates (creates) a particle on site (m, n), where the position in the lattice is defined as
annihilates (creates) a particle on site (m, n), where the position in the lattice is defined as  , with m, n integers and
, with m, n integers and  the unit vectors. In the limit Δ ≫ κ, the effective coupling strengths are given by
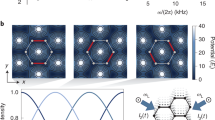
the unit vectors. In the limit Δ ≫ κ, the effective coupling strengths are given by  and Jyeff ≃ Jy; the experimental parameters were chosen such that Jxeff ≈ Jyeff ≡ J. Higher-order corrections to the effective Hamiltonian lead to a local renormalization of the hopping along y, which for our experimental parameters κ/(ℏω) can lead to modifications of the tunnelling up to 0.3Jy (Methods and Supplementary Information). In the presence of the effective flux Φ = π/2, the magnetic unit cell is four times larger than the standard unit cell (Fig. 1a). Consequently the first magnetic Brillouin zone (FBZ) is reduced, and the energy bands split into four subbands3,6. Because the two middle bands touch at the Dirac points (Fig. 2b), the energy spectrum is partitioned into three isolated bands, labelled as Eμ, with Chern numbers νμ. We stress that the central ‘super-band’ contains twice the number of states as compared to the other two bands.
and Jyeff ≃ Jy; the experimental parameters were chosen such that Jxeff ≈ Jyeff ≡ J. Higher-order corrections to the effective Hamiltonian lead to a local renormalization of the hopping along y, which for our experimental parameters κ/(ℏω) can lead to modifications of the tunnelling up to 0.3Jy (Methods and Supplementary Information). In the presence of the effective flux Φ = π/2, the magnetic unit cell is four times larger than the standard unit cell (Fig. 1a). Consequently the first magnetic Brillouin zone (FBZ) is reduced, and the energy bands split into four subbands3,6. Because the two middle bands touch at the Dirac points (Fig. 2b), the energy spectrum is partitioned into three isolated bands, labelled as Eμ, with Chern numbers νμ. We stress that the central ‘super-band’ contains twice the number of states as compared to the other two bands.
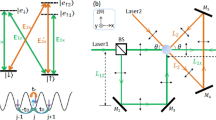
a, Schematic drawing of the Hofstadter-like optical lattice with an additional staggered detuning δ along x and y. b, Energy spectrum as a function of the staggered detuning. For a detuning larger than 2J the bands are topologically trivial, with Chern numbers νμ = 0. At the transition point, the bandgaps close and the system enters a topologically non-trivial phase, where the Chern number of the lowest band ν1 = +1. For vanishing detuning δ = 0, the system realizes the Harper–Hofstadter model with flux Φ = π/2. Note that the vertical energy axis is rescaled for each spectrum.
To load the atoms into the lowest Hofstadter band, we developed an experimental sequence using an auxiliary superlattice potential (Methods), which introduces a staggered detuning δ along both directions: along x, the offset between neighbouring sites is increased away from the resonance condition to Δ + δ, whereas it is simply given by δ along y (Fig. 2a). Importantly, the unit cell of the square lattice with staggered potentials along both directions is equivalent to the magnetic unit cell of the Harper–Hofstadter model; thus, the number of energy bands is preserved during the loading sequence. For δ > 2J the topology of the bands is trivial, all Chern numbers are zero, and the atoms populate the lowest band (low-energy sites of the superlattice). When crossing the topological phase transition at δ = 2J, the spectral gaps close at a single point in the FBZ and the system enters the topologically non-trivial regime, where the lowest band E1 has a Chern number ν1 = +1. Finally, for δ = 0 we realize the Harper–Hofstadter model with flux Φ = π/2 (Fig. 2b).
Recently, several methods were proposed to probe the topological nature of energy bands with cold atoms, exploiting Bloch oscillations and other transport measurements12,13,28. In the presence of a constant force  , atoms on a lattice undergo Bloch oscillations along the direction of the force; this longitudinal motion is captured by the band velocity vμband = ∂kEμ/ℏ. Moreover, when the energy bands have non-zero Berry curvature, the cloud also experiences a net perpendicular (Hall) drift (Fig. 1b); this transverse motion is described by a further contribution to the velocity, denoted vμx (ref. 32). For a particle in a state |uμ(k)〉 of the μth band, this ‘anomalous’ contribution to the velocity reads
, atoms on a lattice undergo Bloch oscillations along the direction of the force; this longitudinal motion is captured by the band velocity vμband = ∂kEμ/ℏ. Moreover, when the energy bands have non-zero Berry curvature, the cloud also experiences a net perpendicular (Hall) drift (Fig. 1b); this transverse motion is described by a further contribution to the velocity, denoted vμx (ref. 32). For a particle in a state |uμ(k)〉 of the μth band, this ‘anomalous’ contribution to the velocity reads

where Ωμ(k) is the Berry curvature of the band32. The effects associated with the anomalous velocity vμx can be isolated by uniformly populating the bands, which averages out any contribution from the band velocity, ∫∂Eμ/∂kx, yd2k = 0. This could be directly realized with fermionic atoms by setting the Fermi energy within a spectral gap13, in analogy with the integer quantum Hall effect. Here we consider an incoherent distribution of bosonic atoms, where the population within each band is homogeneous in k-space, an assumption which has been validated independently (Supplementary Information). In the absence of inter-band transitions, the contribution of the μth band to the centre-of-mass (COM) motion perpendicular to the force can be written in terms of the Chern number of the μth band νμ = ∫ FBZΩμd2k/(2π),

where the factor 4a2 is the area of the magnetic unit cell (Fig. 1a) and τB = h/(Fa) is the characteristic timescale for Bloch oscillations. In our experiments, we applied an optical dipole force along y (Methods) and measured the COM-evolution of the atomic cloud in situ for opposite directions of the flux Φ, which were then subtracted to obtain the differential shift x(t, Φ) − x(t, − Φ) = 2x(t). For short evolution times, an almost linear differential displacement is observed (Fig. 3a), whereas for longer times it saturates owing to band repopulation (Fig. 3b, c). We note that the deflection is symmetric with respect to the direction of the applied force (black and grey data points in Fig. 3b), as expected from theory. Furthermore, we measured the COM-motion for Φ = 0 (light blue data points in Fig. 3b) and for a staggered-flux distribution (dark blue data points in Fig. 3b); neither measurement shows any significant displacement, which is consistent with a Chern number of zero (Methods).
The differential shifts were measured after loading the atoms in the Hofstadter bands (Φ = π/2, J/h = 75(3) Hz) and applying an external force F = ±F êy (Fa/h = 38.4(8) Hz). The value of the differential shift was evaluated after averaging ten images per sign of the flux ±Φ and subsequently subtracting the COM-positions of the atomic cloud. Henceforth we define this as one data set. Each data point is an average of five data sets and the error bars depict the error of the mean. a, The black solid line is a linear fit to the data for t ≤ 35 ms. Taking into account the measured initial band populations ημ0 = {0.55(6), 0.31(3), 0.13(3)} and using equation (2) yields the value νexp = 0.9(2). The dashed line depicts the ideal evolution for ν1 = 1 and the same initial band populations. The green shaded area illustrates the corresponding numerical simulations. These numerics are based on the Hamiltonian in equation (1) supplemented by small higher-order corrections (Supplementary Information). b, The black (faded grey) data points show the evolution for longer times and opposite directions of the applied force F = ±F êy. The small images on the right show typical experimental data obtained after subtracting the averaged images of one data set for ±Φ. a.u., arbitrary units. The blue data points were taken in lattice configurations with trivial topology, Φ = 0 (light blue) and Φ = (−1)mπ/2 (dark blue); the blue solid lines are guides to the eye. The solid black and grey lines show a fit to our data using equation (3) combined with the filling factor γ(t), which was evaluated using the measured band populations ημ(t) shown in (c) and fitted with an exponential. This provides an experimental Chern number νexp = 1.05(12) (black) and νexp = 0.98(12) (grey). c, Evolution of the band populations ημ(t) = N(μ)/Ntot, defined as the fraction of particles in band μ. Each data point is an average of two individual measurements and the error bars denote the standard deviation of the data points. The colour code illustrates the connection to the Hofstadter bands shown in Fig. 2b.
The band-mapping sequence, which is basically the reversed loading sequence as illustrated in Fig. 2b, allows us to measure the band populations of the different Hofstadter bands during the dynamics (Fig. 3c). For large detuning δ, tunnelling is inhibited along both directions and the populations of the Hofstadter bands map onto those of the two-dimensional superlattice, where standard detection techniques can be used to evaluate the band populations ημ (Methods and Supplementary Information)33. The contribution of all atoms in different bands to the mean COM-displacement can be written as

where the filling factor γ0 is given by the initial band populations ημ0 (Fig. 3c). This result is obtained by invoking the particle–hole symmetry inherent to the Harper–Hofstadter model (that is, ν1 = ν3), together with the fact that the sum of Chern numbers necessarily vanishes, ∑μνμ = 0; we have also taken into account that the middle band contains twice the number of states as compared to the other two bands; its contribution to x(t) is thus proportional to ν2(η2/2) = − ν1η2 (Supplementary Information). As a result, the COM-displacement in equation (2) is determined only by the initial band populations ημ0 and the Chern number of the lowest band ν1, under the assumption that the band populations are constant over time, which is reasonable for short times. Comparing the short-time trajectories of the atomic cloud x(t) in Fig. 3a with the equation of motion equation (2), together with the measured initial filling factor γ0, provides a first reasonable experimental value for the Chern number of the lowest band as νexp = 0.9(2). In particular, for short times, we find good agreement between the theoretical predictions based on the effective Hamiltonian and the experimental data.
We now present a more precise Chern-number measurement based on a long-time analysis, which takes into account the repopulation of atoms between the three Hofstadter bands (Fig. 3c). One possible reason for this repopulation is the presence of Landau–Zener transitions, which are neglected in equation (2) but captured well by the numerical simulations (green shaded area in Fig. 3a). However, we observe similar repopulation timescales in the absence of the force, most probably due to heating of the atoms caused by the periodic driving. To capture the band-repopulation effects, we benefit from the measured filling factor γ(t) = η1(t) − η2(t) + η3(t) and model the dynamics according to the modified equations of motion

By fitting this equation to the experimental data x(t), with the Chern number being the only fit parameter, we obtain an experimental value for the Chern number of the lowest band

Here we averaged over four independent Chern-number measurements, two for each direction of the gradient to avoid systematic errors (see inset of Fig. 4a). The stated uncertainty is the standard deviation obtained from these measurements. This shows that including our time-resolved band-mapping data into our modelling of the transverse Hall drift leads to a very good understanding of the full time dynamics, and allows us to extract the value of the Chern number with high accuracy. The applied force was chosen to be strong enough to accurately detect the displacement, but weak enough to limit nonlinear effects and Landau–Zener-induced inter-band transitions.
a, For each value of the gradient, we measured the full time evolution of the differential shift and filling factor γ(t) (similar to the evolution shown in Fig. 3b, c) to extract the value of the Chern number. The solid line is a guide to the eye to highlight the saturation to νexp ≈ 1 for small gradients. The green data point depicts the experimentally determined Chern number νexp = 0.99(5) for ±Fa/h = 38.4(8) Hz, for which a larger number of measurements were taken, as shown in the inset. b, The differential shift versus detuning was measured after four different times t = (20,50,100,150) ms for Fa/h = 38.4(8) Hz to fit the Chern number based on the measured filling factor γ(t). The topological phase transition, which is expected at δ = 2J for the model (Fig. 2b), is smoothened owing to experimental uncertainties (green solid curve). The blue shaded area illustrates the range of transition points δ = 1.77(14)J given by the second-order correction, for our experimental parameters κ/(ℏω) = 0.58(2) (Methods and Supplementary Information). The green and blue curves are calculated taking into account the experimental uncertainty in the detuning (0.4J, horizontal error bars), which is determined experimentally by typical drifts and fluctuations of the resonance frequency. All data points include an average of five data sets for each time step for the differential shift and two measurements for γ(t). As in (a) the green data point depicts the experimentally determined Chern number νexp = 0.99(5) for δ = 0. All vertical error bars show the uncertainty resulting from the fit error of γ(t).
The dependence of our Chern-number measurement with respect to the force was studied in more detail, as shown in Fig. 4a. For gradient strengths smaller than the bandgap, Fa < Egap ≈ 1.5J, the experimental value for the Chern number saturates to νexp ≈ 1, indicating that it can be determined reliably for small forces. For very strong forces, Fa > Egap, our model breaks down and the experimental value νexp decreases to zero.
Finally, we characterized the topological phase transition, which is expected for a staggered detuning of δ = 2J (Fig. 2). For this analysis, we set the gradient amplitude to the value Fa = 38.4(8) Hz × h = 0.51(1)J, which is well below the bandgap for δ = 0. In agreement with theory, we observe that the experimental value for the Chern number decreases to zero across the phase transition (Fig. 4b). We note that Landau–Zener transitions to higher bands become more important when approaching the transition (gap-closing point); however, this should not affect the measurement because the band repopulation is taken into account, according to equation (3). The smoothened transition is most probably due to the experimental uncertainties in the resonance condition (green solid line in Fig. 4b). Furthermore, second-order corrections to the effective Hamiltonian shift the transition point to a mean value of δ ≈ 1.8J for our experimental parameters κ/(ℏω) = 0.58(2) (solid blue line and shaded region in Fig. 4b, see Methods and Supplementary Information).
In conclusion, we have successfully implemented a method to measure the Chern number in a cold-atom set-up, which can be generalized to a wide range of non-electronic systems, including ion traps9, photonic crystals10 and polaritons11. Although our measurement accommodates dynamical transitions to higher bands, which we attribute to the lattice modulation used to engineer the topological band structure, our results highlight the necessity to further deepen the understanding of heating processes in periodically driven quantum systems. Minimizing heating effects and clarifying the role of interactions in these modulated systems will be crucial in view of reaching topological strongly correlated states in Chern bands, such as fractional Chern insulators7.
Recently we have become aware of related measurements showing signatures of the Berry curvature in periodically modulated honeycomb optical lattices34.
Methods
Loading sequence.
The experimental sequence started by loading a Bose–Einstein condensate of 87Rb atoms within 150 ms into a two-dimensional optical superlattice. Along each of the axes two standing waves were superimposed with λs = 767 nm and λL = 2λs. The relative phase between them was chosen such that a lattice potential with staggered energy offsets Δ + δx along x and δy along y, with δx ≈ δy ≡ δ and δ < Δ, was created. The lattice depths were Vy = 10(1) Ers, VyL = 1.75(5) ErL, Vx = 6.0(2) Ers and VxL = 5.25(16) ErL, with Erα = ℏ2kα2/(2m), α = {s, L}. At this point of the sequence all atoms were loaded into the low-energy sites. The two pairs of beams used for the modulation were then switched on in 30 ms, with a frequency difference ωr = −ωb = ±Δ/ℏ; at this stage, no resonant tunnelling between neighbouring sites was induced, owing to the offset detuning δ. After that, we ramped down the long lattices within 30 ms to VyL = 0 ErL and VxL = 3.25(10) ErL, which corresponds to δ = 0. For these values, resonant laser-assisted tunnelling along x and bare tunnelling along y occurred, simultaneously creating a homogeneous flux Φ = ±π/2 (aligned along  ) depending on the sign of the modulation frequency. We checked that all lattice sites were equally populated after the loading sequence.
) depending on the sign of the modulation frequency. We checked that all lattice sites were equally populated after the loading sequence.
Loading sequence for lattice set-up with trivial topology.
The loading sequence described above is also used to load the atoms into the staggered flux lattice. The only difference is that the modulation is switched on with a frequency difference ωr = ωb = ±Δ/ℏ, which results in a flux Φ = ±(−1)mπ/2.
The sequence for the lattice without flux was performed in a similar manner. It started by loading the atoms into a two-dimensional superlattice with lattice depths Vx = Vy = 10(1) Ers, VxL = VyL = 1.75(5) ErL within 150 ms. Subsequently, the long lattices were decreased to zero within 30 ms. In this way a simple square lattice configuration without flux and a tunnel coupling of J/h = 75(3) Hz along both directions was realized.
Optical gradient.
The optical gradient used to induce Bloch oscillations along y was realized using a further laser beam with wavelength λz = 844 nm. It was focused at the atom position to a waist of about 125 μm and aligned such that the atomic cloud is located at the maximum slope of the Gaussian beam profile along y. Along x the beam was centred on the atom position. The strength of the gradient was determined through independent measurements of Bloch oscillations in a one-dimensional lattice with Vy = 10(1) Ers.
Band-mapping sequence.
To measure the populations in different Hofstadter bands, we reversed our loading sequence described above and ramped up the long lattices to VyL = 1.75(5) ErL and VxL = 5.25(16) ErL, respectively, within 30 ms. At this point of the sequence, tunnelling is off-resonant along both directions, and the Hofstadter bands map onto the bands of the usual 2D superlattice. We then suddenly switched off the modulation and used standard detection techniques to infer the momentum distribution and band populations (Supplementary Information).
The effective Hamiltonian.
The set-up is described by a time-dependent Hamiltonian  , where the static part
, where the static part  includes the nearest-neighbour hopping terms, the staggered lattice potential (with energy offset Δ + δ along x, and δ along y) and the external confinement. The main offset Δ ≫ Jx is chosen so as to inhibit the tunnelling along the x direction. The time-periodic modulation
includes the nearest-neighbour hopping terms, the staggered lattice potential (with energy offset Δ + δ along x, and δ along y) and the external confinement. The main offset Δ ≫ Jx is chosen so as to inhibit the tunnelling along the x direction. The time-periodic modulation  with frequency ω is created by two pairs of laser beams, and it is resonant with the offset ω = Δ/ℏ; it simultaneously restores the tunnelling along x and generates space-dependent Peierls phases, effectively creating a uniform flux Φ = 2π(1/4) per plaquette. The modulation also modifies the tunnelling matrix elements along the y direction. In the high-frequency limit, ℏω ≫ Jx, Jy, the system is described well by the effective Harper–Hofstadter Hamiltonian in equation (1). Adding weak higher-order corrections to the latter, and considering a non-zero staggered detuning δ ≪ Δ, leads to a Hamiltonian, whose momentum representation is given by the 4 × 4 matrix
with frequency ω is created by two pairs of laser beams, and it is resonant with the offset ω = Δ/ℏ; it simultaneously restores the tunnelling along x and generates space-dependent Peierls phases, effectively creating a uniform flux Φ = 2π(1/4) per plaquette. The modulation also modifies the tunnelling matrix elements along the y direction. In the high-frequency limit, ℏω ≫ Jx, Jy, the system is described well by the effective Harper–Hofstadter Hamiltonian in equation (1). Adding weak higher-order corrections to the latter, and considering a non-zero staggered detuning δ ≪ Δ, leads to a Hamiltonian, whose momentum representation is given by the 4 × 4 matrix

where κ is the modulation strength, J/h ≈ 75 Hz is the effective tunnelling amplitude, ϕ0 is the phase of the modulation relative to the underlying lattice (Supplementary Information), and the lattice spacing is a = 1. In the experiment, κ/(ℏω) ≈ 0.58, so that the inhomogeneous corrections to the hopping along the y direction (that is, h1 and h2) are not negligible.
References
Karplus, R. & Luttinger, J. M. Hall effect in ferromagnetics. Phys. Rev. 95, 1154–1160 (1954).
Von Klitzing, K. The quantized Hall effect. Rev. Mod. Phys. 58, 519–531 (1986).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).
Dean, C. R. et al. Hofstadter’s butterfly and the fractal quantum Hall effect in moiré superlattices. Nature 497, 598–602 (2013).
Ponomarenko, L. A. et al. Cloning of Dirac fermions in graphene superlattices. Nature 497, 594–597 (2013).
Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976).
Parameswaran, S. A., Roy, R. & Sondhi, S. L. Fractional quantum Hall physics in topological flat bands. C. R. Phys. 14, 816–839 (2013).
Goldman, N., Juzeliunas, G., Ohberg, P. & Spielman, I. B. Light-induced gauge fields for ultracold atoms. Preprint at http://arXiv.org/abs/1308.6533 (2013)
Bermudez, A., Schaetz, T. & Porras, D. Synthetic gauge fields for vibrational excitations of trapped ions. Phys. Rev. Lett. 107, 150501 (2011).
Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).
Carusotto, I. & Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 85, 299–366 (2013).
Price, H. M. & Cooper, N. R. Mapping the Berry curvature from semiclassical dynamics in optical lattices. Phys. Rev. A 85, 033620 (2012).
Dauphin, A. & Goldman, N. Extracting the Chern number from the dynamics of a Fermi gas: Implementing a quantum Hall bar for cold atoms. Phys. Rev. Lett. 111, 135302 (2013).
Aidelsburger, M. et al. Experimental realization of strong effective magnetic fields in an optical lattice. Phys. Rev. Lett. 107, 255301 (2011).
Aidelsburger, M. et al. Realization of the Hofstadter Hamiltonian with ultracold atoms in optical lattices. Phys. Rev. Lett. 111, 185301 (2013).
Atala, M. et al. Direct measurement of the Zak phase in topological Bloch bands. Nature Phys. 9, 795–800 (2013).
Abanin, D. A., Kitagawa, T., Bloch, I. & Demler, E. Interferometric approach to measuring band topology in 2D optical lattices. Phys. Rev. Lett. 110, 165304 (2013).
LeBlanc, L. J. et al. Observation of a superfluid Hall effect. Proc. Natl Acad. Sci. USA 109, 10811–10814 (2012).
Harper, P. G. Single band motion of conduction electrons in a uniform magnetic field. Proc. Phys. Soc. A 68, 879–892 (1955).
Azbel, M. Y. Energy spectrum of a conduction electron in a magnetic field. Zh. Eksp. Teor. Fiz. 46, 929–946 (1964) [Sov. Phys. JETP 19, 634–645 (1964)]
Jaksch, D. & Zoller, P. Creation of effective magnetic fields in optical lattices: The Hofstadter butterfly for cold neutral atoms. New J. Phys. 5, 56 (2003).
Gerbier, F. & Dalibard, J. Gauge fields for ultracold atoms in optical superlattices. New J. Phys. 12, 033007 (2010).
Mueller, E. J. Artificial electromagnetism for neutral atoms: Escher staircase and Laughlin liquids. Phys. Rev. A 70, 041603 (2004).
Kolovsky, A. R. Creating artificial magnetic fields for cold atoms by photon-assisted tunneling. Europhys. Lett. 93, 20003 (2011).
Baur, S. K., Schleier-Smith, M. H. & Cooper, N. R. Dynamic optical superlattices with topological bands. Phys. Rev. A 89, 051605 (2014).
Miyake, H., Siviloglou, G. A., Kennedy, C. J., Burton, W. C. & Ketterle, W. Realizing the Harper Hamiltonian with laser-assisted tunneling in optical lattices. Phys. Rev. Lett. 111, 185302 (2013).
Sørensen, A. S., Demler, E. & Lukin, M. D. Fractional quantum Hall states of atoms in optical lattices. Phys. Rev. Lett. 94, 086803 (2005).
Goldman, N. & Dalibard, J. Periodically-driven quantum systems: Effective Hamiltonians and engineered gauge fields. Phys. Rev. X 4, 031027 (2014).
Bukov, M., D’Alessio, L. & Polkovnikov, A. Universal high-frequency behavior of periodically driven systems: From dynamical stabilization to Floquet engineering. Preprint at http://arXiv.org/abs/1407.4803 (2014)
Lignier, H. et al. Dynamical control of matter-wave tunneling in periodic potentials. Phys. Rev. Lett. 99, 220403 (2007).
Struck, J. et al. Quantum simulation of frustrated classical magnetism in triangular optical lattices. Science 333, 996–999 (2011).
Xiao, D., Chang, M-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Nascimbène, S. et al. Experimental realization of plaquette resonating valence-bond states with ultracold atoms in optical superlattices. Phys. Rev. Lett. 108, 205301 (2012).
Jotzu, G. et al. Experimental realisation of the topological Haldane model. Preprint at http://arXiv.org/abs/1406.7874 (2014)
Acknowledgements
We acknowledge fruitful discussions with J. Dalibard and also with A. Dauphin, P. Gaspard, F. Gerbier, F. Grusdt, I. Carusotto, T. Ozawa and H. Price. This work was supported by NIM, the EU (UQUAM, SIQS) and EPSRC Grant No. EP/K030094/1. M.Aidelsburger was further supported by the Deutsche Telekom Stiftung, M.L. by ExQM and N.G. by the Université Libre de Bruxelles and the FRS-FNRS (Belgium).
Author information
Authors and Affiliations
Contributions
M.Aidelsburger, M.L. and C.S. performed the experiment. All authors contributed to the design of the experiment, the theoretical and data analysis, and to the writing of the paper. I.B. and N.G. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 1120 kb)
Rights and permissions
About this article
Cite this article
Aidelsburger, M., Lohse, M., Schweizer, C. et al. Measuring the Chern number of Hofstadter bands with ultracold bosonic atoms. Nature Phys 11, 162–166 (2015). https://doi.org/10.1038/nphys3171
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3171
This article is cited by
-
Injection spectroscopy of momentum state lattices
Communications Physics (2024)
-
Realization of a fractional quantum Hall state with ultracold atoms
Nature (2023)
-
Quantization and its breakdown in a Hubbard–Thouless pump
Nature Physics (2023)
-
Simulating Chern insulators on a superconducting quantum processor
Nature Communications (2023)
-
Quantized fractional Thouless pumping of solitons
Nature Physics (2023)