Abstract
Quantum entanglement is the central resource behind quantum information science, from quantum computation and simulation1,2 to enhanced metrology3 and secure communication1. These applications require the quantum control of large networks of qubits to realize gains and speed increases over conventional devices. However, propagating entanglement becomes difficult or impossible as the system grows in size. Here, we demonstrate the first step in a modular approach4 to scaling entanglement by using complementary quantum buses on a collection of three atomic ion qubits stored in two remote ion trap modules. Entanglement within a module is achieved with deterministic near-field interactions through phonons5, and remote entanglement between modules is achieved with a probabilistic interaction through photons6. This minimal system allows us to address generic issues in the synchronization of entanglement with multiple buses. It points the way towards a modular large-scale quantum information architecture that promises less spectral crowding and thus potentially less decoherence as the number of qubits increases4. We generate this modular entanglement faster than the observed remotely entangled qubit-decoherence rate, showing that entanglement can be scaled simply by adding more modules.
Similar content being viewed by others
Main
Small modules of qubits have been entangled through native local interactions in many physical platforms, such as trapped atomic ions through their Coulomb interaction5, Rydberg atoms through their electric dipoles7,8, nitrogen-vacancy centres in diamond through their magnetic dipoles9, and superconducting Josephson junctions through capacitive or inductive couplings10,11. However, each of these systems is confronted with practical limits to the number of qubits that can be reliably controlled, stemming from inhomogeneities, the complexity and density of the interactions between the qubits, or quantum decoherence. Scaling beyond these limits can be achieved by invoking a second type of interaction that can extend the entanglement to other similar qubit modules. Such an architecture should therefore exploit both the local interactions within the qubit modules, and also remote interactions between modules (an example architecture is shown in Fig. 1). One promising approach is to directly move qubits between different modules12,13, but this approach is limited by the difficulty of moving qubits over large distances. Optical interfaces provide ideal buses for extending entanglement between modules14,15, as optical photons can propagate over macroscopic distances with negligible loss. Several qubit systems have been entangled through remote optical buses, such as atomic ions16, neutral atoms17 and nitrogen-vacancy centres in diamond18.
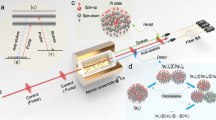
a, Two modules separated by ∼1 m each contain an ion trap. High numerical aperture objectives couple spontaneously emitted photons from a single atom into a single-mode optical fibre. The photons from atoms in separate traps interfere on a 50/50 beamsplitter (BS), are sorted by polarizing beamsplitters (PBS), then detected by photomultiplier tubes (PMTs). Coincident detection of photons on specific PMT pairs heralds entanglement of atomic spins (Methods). b, Schematic of a large-scale, modular quantum network of trapped ions. Ion trap modules (red boxes) confine atoms coupled together through their Coulomb bus, and entanglement within modules is accomplished with the application of spin-dependent forces on the trapped atoms4. Probabilistic, heralded entanglement is generated between modules via interference of emitted photons from each module. A reconfigurable N × N cross-connect switch links arbitrary modules. Photon interference occurs at fibre beamsplitters, and a single-photon detector array heralds entanglement of atomic spins between modules.
In the experiment reported here, we juxtapose local phonon and remote photon entanglement buses using trapped atomic ion qubits, balancing the requirements of each interface within the same qubit system. The observed entanglement rate within and between modules is faster than the observed entangled qubit-decoherence rate. This is critical in quantum modular architectures because the required resource scaling is superexponential in the ratio of decoherence rate to entanglement rate4. This ratio is observed to be 0.2 in this experiment, many orders of magnitude lower than previous experiments demonstrating remote entanglement17,18,19. Overcoming the resource scaling requirement makes trapped ions a leading candidate for realizing a quantum network.
The qubits in this experiment are defined by the two hyperfine ‘clock’ states, |F = 0, mF = 0〉 ≡ |0〉 and |F = 1, mF = 0〉 ≡ |1〉, which are separated by ω0 = 2π × 12.64282 GHz in the 2S1/2 manifold of trapped 171Yb+ atoms. Laser cooling, optical pumping, and readout occur via standard state-dependent fluorescence techniques20. The qubits are trapped in two independent modules separated by ∼1 m, as shown in Fig. 1a. (The ion traps, light collection optics and interferometer could in principle be part of a modular, scalable architecture, as shown in Fig. 1b.)
To generate remote entanglement between atoms in physically separated ion trap modules, we synchronously excite each atom with a resonant fast laser pulse16. A fraction of the resulting spontaneously emitted light is collected into an optical fibre, with each photon’s polarization (σ+ or σ−) entangled with its parent atom owing to atomic selection rules (Fig. 2a). Each photon passes through a quarter-wave plate that maps circular to linear polarization (σ+ → H and σ− → V), and then the two photons interfere on a 50/50 beamsplitter, where detectors monitor the output (see Fig. 1a and Methods)19. We select the two-photon Bell states of light |HV〉 + |VH〉, where ϕD is 0 or π depending on which pair of detectors registers the photons21. Finally, a series of microwave pulses transfers the atoms into the {|0〉, |1〉} basis (Fig. 2b), ideally resulting in the heralded entangled state of the two remote atomic qubits |01〉 + |10〉.
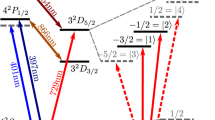
a, Resonant excitation scheme and single-photon emission in an Yb+ atom system. After optically pumping the atoms to the |F, mF〉 = |0,0〉 state of the 2S1/2 manifold, a frequency-doubled, mode-locked Ti:sapphire laser excites the atom to the |1,0〉 state of the 2P1/2 manifold, whereby the atom decays to the |1, ±1〉 states via emission of σ∓ polarized photons into optical fibres. b, After interference of the two photons on a 50/50 non-polarizing beamsplitter, we apply a series of microwave transfer pulses to transfer the entangled state to the clock basis, resulting in the state |01〉 + |10〉, where ϕAB is the intermodular phase. c, We entangle atomic spins within module A through spin-dependent optical dipole forces using off-resonant lasers (purple arrows)5,23.
The intermodular phase is given by

In this equation, the phase evolves with the difference in qubit splittings between module A and B, ΔωAB = ω0, A − ω0, B ≈ 2π × 2.5 kHz, owing to controlled Zeeman shifts20. The stable geometric phase factors kcΔτ < 10−2 and kΔx < 10−2 result from the difference in excitation time Δτ < 100 ps and difference in path length Δx < 3 cm between each atom and the beamsplitter. Here c is the speed of light and k ∼ 0.33 m−1 is the wavenumber associated with the energy difference of the photon decay modes (here, the energy difference between σ+ and σ− photons). The final contribution is the stable phase difference of the microwave transfer pulses ΔϕT across the modules.
In previous experiments, entanglement between remote atom spins at rates of 0.002 s−1 was accomplished using atom–photon frequency entanglement22, and at rates of 0.026 s−1 using atom–photon polarization entanglement19. Here, we greatly increase the single-photon collection efficiency by using high numerical aperture microscope objectives and detecting two out of four Bell states of light emitted by the atoms to achieve a heralded entanglement rate of 4.5 s−1 (Methods).
Given a heralded photon coincidence event, we verify entanglement between ion trap modules by measuring atomic state populations and coherences following standard two-qubit tomography protocols23. We measure an average entangled Bell state fidelity of 0.78 ± 0.03. Imperfect mode matching at the beamsplitter contributes 0.08 ± 0.02 to the infidelity. The measured atom–photon polarization entanglement is 0.92 per ion trap, which contributes 0.15 to the remote entangled state infidelity. We attribute the atom–photon polarization infidelity to spatially inhomogeneous rotations of the photon polarization, polarization-dependent loss, and multiple excitations of the remote atoms from imperfect pulse picking of resonant fast laser pulses. Combining imperfect ion–photon polarization entanglement with imperfect mode matching at the beamsplitter yields an expected fidelity of 0.79 ± 0.02, consistent with observation. This fidelity could be improved with the use of fibre beamsplitters to improve spatial mode matching of the photons. In addition, the use of phase masks could correct polarization error introduced by optical elements associated with single-photon collection and transmission. Electro-optic pulse pickers with higher extinction ratios could reduce errors associated with multiple excitations of remote atoms in different modules.
Because the phase of the entangled state evolves in time (second term of equation (1)), the remote atomic entanglement coherence time can be measured with Ramsey spectroscopy. Unlike a Ramsey experiment with a single atom, this measurement is not sensitive to long-term stability of the local oscillator20,24. We measure the remote entangled state coherence time by repeating the above experiment with constant transfer pulse phase ΔϕT while varying the Ramsey zone delay before a final π/2 microwave rotation. We use a spin-echo pulse in the middle of the Ramsey zone delay to account for slow magnetic field gradient drifts, and measure an entanglement coherence time of 1.12 s, well in excess of the required time to create remote entanglement between modules (Fig. 3c). Our experiment thus crosses the threshold where fault-tolerant error correction can propagate entanglement without a superexponential overhead in resources4.
a, Populations of two remote atoms after heralding entanglement between modules. After detecting the photon Bell states (ϕD = 0 or π), microwave transfer pulses rotate the remote atom populations to the {|0〉, |1〉} basis. Subsequent detection of the remotely entangled atoms results in measurement of odd parity, P(01) + P(10), with high probability. b, Phase coherent time evolution of the remote entangled state with the application of an intermodular magnetic field gradient. After heralding remote entanglement between modules and applying microwave transfer pulses, the addition of a time delay before a π/2 rotation on both atoms results in an out-of-phase oscillatory behaviour of the remote atom entangled state with ϕD = 0 or π (blue squares and red circles respectively, see equation (1)). c, Remote entangled state coherence and generation probability versus time. We measure the remote entangled state coherence time by adding a Ramsey zone delay in the presence of an intermodular magnetic field gradient before application of a spin-echo pulse and a π/2 microwave rotation, as described in the text. The decay of the fidelity from the measured loss of phase coherence of the entangled state points to magnetic field gradient noise as the dephasing mechanism. A fit to an exponential function yields a coherence time of 1.12 s. The probability of generating entanglement after a given time interval is shown in red. A fit to an exponential function gives the average remote entanglement rate 4.5 s−1. Error bars in a–c (not shown for clarity) are ±1.4% due to state detection error (Methods).
In addition to using a photonic interconnect between ion traps, we use the Coulomb-coupled transverse phonon modes of the atoms to create entanglement within one module (Fig. 2c). Off-resonant laser beams drive stimulated Raman transitions between the qubit levels and impart spin-dependent forces detuned from the phonon modes. Following conventional Coulomb gate protocols5,25, after a certain time the motion returns to its original state (Methods), and the four two-qubit basis states are ideally mapped to the following entangled states

where ϕA is the intramodular phase from this optical Raman process in module A (ref. 26). This phase depends on the relative optical phase of two non-copropagating lasers. Using the above gate operation on two Doppler-cooled atoms within a module ( ), we create the state |00〉 − |11〉 with a fidelity of 0.85 ± 0.01, excluding detection error, as shown in Fig. 4a, b. Cooling below the Doppler limit was not implemented in this experiment to keep the experimental repetition rate high for fast generation of remote entanglement. Higher-fidelity Coulomb gates may be achieved by better control of the RF amplitude applied to the ion trap and through the use of ground state cooling to reduce sensitivity to small detuning errors from the trapped atoms’ sidebands of motion.
), we create the state |00〉 − |11〉 with a fidelity of 0.85 ± 0.01, excluding detection error, as shown in Fig. 4a, b. Cooling below the Doppler limit was not implemented in this experiment to keep the experimental repetition rate high for fast generation of remote entanglement. Higher-fidelity Coulomb gates may be achieved by better control of the RF amplitude applied to the ion trap and through the use of ground state cooling to reduce sensitivity to small detuning errors from the trapped atoms’ sidebands of motion.
a, After preparing the atoms in the state |00〉 and applying an entangling gate through phonons within a module (equation (2)), we measure the parity of the entangled state following π/2 qubit rotations with variable phase ϕ with respect to the intramodular phase ϕA of the two atoms. The amplitude of the parity oscillation is 0.79 ± 0.02 and the fidelity of the entangled state is 0.85 ± 0.01 excluding state detection errors. b, Populations of two atoms in ion trap module A after remote entanglement between atoms 2 and 3 followed by entanglement between atoms 1 and 2, as described in the text. After measuring the resulting three-particle state (equation (3)), if the remote atom is in the state |1〉, atoms 1 and 2 should be in an even parity state. If the remote atom is in the state |0〉, atoms 1 and 2 should be in an odd parity state. We observe this correlation with the remote atom with probability 0.71 ± 0.04 and 0.75 ± 0.05, respectively, after averaging over detection of the entangled photon states. c, Parity oscillation of atoms 1 and 2 conditioned on detecting the remote atom in the state |1〉B (red squares) and |0〉B (blue circles). After remote entanglement between modules and entanglement within one module, we apply a Raman π/2 rotation with variable phase ϕ to atoms 1 and 2 in module A and measure the state of all three atoms. If the remote atom is in the state |0〉B, a π/2 rotation on atoms 1 and 2 maps |ψ1ψ2〉A = |01〉A − i |10〉A to a state with zero average parity for any phase ϕ of the rotation. If the remote atom is in the state |1〉B, a π/2 rotation with variable phase ϕ of |ψ1ψ2〉A = |00〉A − |11〉A maps the parity of this state to cos(ϕA − 2ϕ). We observe such a parity oscillation correlated with the state of the remote atom. The fidelity of the two-qubit entangled state |00〉A − |11〉A conditioned on detecting the remote atom in |ψ3〉B = |1〉B is 0.63 ± 0.03. Error bars in a–c are the fit error of experimental histograms of the two qubits’ four basis states.
We now describe the integration of both photonic and phononic buses to generate entangled three-particle states. The three atoms are first prepared in the state |ψ1ψ2〉A |ψ3〉B = |00〉A |0〉B, with atoms 1 and 2 in module A and the remote atom 3 in module B (Fig. 1a). After heralding entanglement between atom 2 in module A and atom 3 in module B using photons, we re-initialize atom 1 to the state |0〉A with an individual addressing optical pumping beam, and then we entangle atoms 1 and 2 within module A using phonons. Ideally, this produces the state

In the above state, the parity of any pair of atoms is correlated with the spin state of the third atom. We take advantage of this property to probe the parity of atoms 1 and 2 in module A, and correlate it with the state of remote atom 3 in module B. After making photon and phonon connections between the atoms, we apply a π/2 Raman rotation to atoms 1 and 2 with a variable phase ϕ, followed by state detection of all three atoms. When the remote atom is measured in state |ψ3〉B = |1〉, the spin parity of atoms 1 and 2 in module A is Π = Πc cos(ϕA − 2ϕ). When the remote atom is measured in state |ψ3〉 = |0〉B, the atoms in module A should be mapped to a state with zero average parity, regardless of the phase of the π/2 Raman rotation. We observe this correlation with a remote entangled state generation rate of ∼4 s−1, as shown in Fig. 4b, c. The fidelity of detecting the state |00〉A − |11〉A of atoms 1 and 2 conditioned on detecting the remote atom 3 in the state |1〉B is 0.63 ± 0.03.
Scaling this architecture to many modules can vastly simplify the complexity of phases to be tracked and controlled. For N ≫ 1 modules each with n ≫ 1 qubits and m ≪ n optical ports at each module, the number of overall phases is reduced by a factor of 1/N + (m/n)2 compared to that for a fully connected set of nN qubits4. Of course, in a modular architecture there may be overheads associated with the reduced connectivity, but it will be useful to have flexibility in this trade-off.
The intermodular phase ϕAB in the experiment is easily controlled by setting the phase difference of microwave rotations between the two modules. The intramodular phase ϕA is determined by the optical phase difference of the two Raman lasers and is passively stable for a single entangling experiment for typical gate times of the order of 100 μs. Tracking and controlling the optical phases between many entangled pairs in spatially separated modules at different times can be accomplished by using ‘phase insensitive’ gates26. All phases introduced by qubit rotations and entangling operations between and within modules can be referenced to a common, high-quality master oscillator27.
Scaling this system will also require mitigating crosstalk within modules. For example, when generating photons for intermodular entanglement, laser scatter and radiated light will disturb neighbouring qubits within a module. This may require the use of different species of atoms as photonic and memory qubits. Quantum information could then be transferred from the photonic qubits to the memory qubits via the Coulomb bus28. The second (photonic) species can also be used for intermittent sympathetic cooling29.
The modular architecture demonstrated in this experiment can be expanded to include many modules. Here an optical cross-connect switch can create a flexible, reconfigurable photonic network between modules (Fig. 1b) and thus be made fault tolerant for the execution of extended quantum circuits4. Modular architectures may be used as the backbone of a quantum repeater network30 and of a quantum network of clocks31. The distance between nodes may be increased with the development of low-loss ultraviolet fibres or the efficient down-conversion of photons to telecommunication wavelengths, without affecting the entanglement rate, enabling long-distance quantum networks32.
Methods
In this experiment, ion trap module A is a segmented, four-blade design useful for holding chains of trapped atoms. A trap drive frequency of 37.15 MHz is used to achieve secular transverse frequencies of ∼2.4 MHz. Module B is a four-rod Paul trap that confines a single atom. This trap is driven at 37.72 MHz to achieve secular frequencies of ∼1.5 MHz.
To generate remote entanglement between atoms in physically separated ion traps, we optically pump both atoms to the |0,0〉 state. A picosecond laser pulse resonant with the 2S1/2 → 2P1/2 transition excites trapped atoms in different modules. The atoms spontaneously emit photons, of which ∼10% are collected by a large NA = 0.6 single-atom microscope objective, resulting in the entangled photon-polarization, atom-spin state 1/2(|1,1〉 |σ−〉 − |1, − 1〉 |σ+〉)⊗2. The emitted photons pass through quarter-wave plates to convert the photon polarization to linear horizontal (H) or linear vertical (V), resulting in the atom–photon state (|1,1〉 |V 〉 − i |1, − 1〉 |H〉)⊗2. Each objective is mode matched to a single-mode optical fibre which delivers the photons to an interferometer with a 50/50 beamsplitter as the central element. The interferometer effects a Bell state measurement of the photon state. We detect two out of the four possible Bell states of light exiting the beamsplitter to herald the entanglement of the remote atoms’ spins21; after a series of microwave transfer pulses, the remote atom entangled state is |01〉 + |10〉, with the intermodular phase ϕAB defined in the main text. The phase ϕD is 0 if coincident photons are detected on PMTs 1 and 2 or 3 and 4 (Fig. 1a). The phase ϕD is π if coincident photons are detected on PMTs 1 and 3 or 2 and 4.
The remote entanglement rate is limited by the collection and detection efficiency of emitted photons from the atoms. The probability for coincident detection of two emitted photons on exciting both atoms simultaneously with a resonant laser pulse is P = pBell[PπQETfibTopt(Ω/4π)]2 = 9.7 × 10−6, where Pπ = 0.95 is the probability of exciting the atom with a resonant 2S1/2 → 2P1/2 laser pulse, = 0.995 is the probability to decay from 2P1/2 → 2S1/2 (as opposed to the 2D3/2 state), pBell = 1/2 accounts for selecting two of the four possible Bell states of light, QE ≈ 0.35 is the quantum efficiency of the single-photon PMT detectors, Tfib ≈ 0.14 is the fibre coupling and transmission probability of a single-mode optical fibre, Topt = 0.95 is the photon transmission through optical components and (Ω/4π) = 0.1 is the fraction of the solid angle each microscope objective subtends. The experimental repetition rate of 470 kHz is limited by the need for Doppler cooling (adding ∼500 ns on average to the repetition time), the atomic state lifetime of the 2P1/2 state (necessitating ∼1 μs of optical pumping for state preparation of the pure quantum state |0〉), and sound wave propagation time in the acousto-optic modulator crystals used in the experiment. These factors result in a measured atom–atom entanglement rate of 4.5 s−1.
The Coulomb entangling gate makes use of Walsh function modulation W[1] to reduce the sensitivity of the gate to detuning and timing errors33. We pick a detuning δ from a transverse mode of motion and set the gate time tg = 2/δ with a π phase advance of the sidebands at t = tg/2. We adjust the average Raman laser intensity power to make the sideband Rabi frequency ηΩ satisfy δ = 23/2ηΩ to complete the entangling gate |00〉 → |00〉 − |11〉 in ion trap module A.
Detection error of a single atom in an ion trap module is limited by off-resonant pumping from the F = 1 to the F = 0 manifold of the 2S1/2 ground state through the F = 1 manifold of the 2P1/2 excited state20—it is ∼1% in the experiments presented here. Detection error of two qubits in the same module is limited by the use of a single PMT detector, where the photon detection histograms of a single qubit in the state |1〉 and two qubits in the state |11〉 may overlap. This overlap is ∼8% in these experiments.
References
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).
Quantum simulation. Nature Phys. 8, (Insight issue) 263–299 (2012).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum metrology. Phys. Rev. Lett. 96, 010401 (2006).
Monroe, C. et al. Large scale modular quantum computer architecture with atomic memory and photonic interconnects. Phys. Rev. A 89, 022317 (2014).
Blatt, R. & Wineland, D. J. Entangled states of trapped atomic ions. Nature 453, 1008–1015 (2008).
Duan, L-M. & Monroe, C. Colloquium: Quantum networks with trapped ions. Rev. Mod. Phys. 82, 1209–1224 (2010).
Isenhower, L. et al. Demonstration of a neutral atom controlled-NOT quantum gate. Phys. Rev. Lett. 104, 010503 (2010).
Wilk, T. et al. Entanglement of two individual neutral atoms using Rydberg blockade. Phys. Rev. Lett. 104, 010502 (2010).
Dolde, F. et al. Room-temperature entanglement between single defect spins in diamond. Nature Phys. 9, 139–143 (2013).
Dicarlo, L. et al. Preparation and measurement of three-qubit entanglement in a superconducting circuit. Nature 467, 574–578 (2010).
Neeley, M. et al. Generation of three-qubit entangled states using superconducting phase qubits. Nature 467, 570–573 (2010).
Kielpinski, D., Monroe, C. & Wineland, D. J. Architecture for a large-scale ion-trap quantum computer. Nature 417, 709–711 (2002).
Barrett, M. et al. Deterministic quantum teleportation of atomic qubits. Nature 429, 737–739 (2004).
Cirac, J. I., Zoller, P., Kimble, H. J. & Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221–3224 (1997).
Duan, L-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Moehring, D. L. et al. Entanglement of single-atom quantum bits at a distance. Nature 449, 68–71 (2007).
Nölleke, C. et al. Efficient teleportation between remote single-atom quantum memories. Phys. Rev. Lett. 110, 140403 (2013).
Pfaff, W. et al. Unconditional quantum teleportation between distant solid-state quantum bits. Science 345, 532–535 (2014).
Matsukevich, D. N., Maunz, P., Moehring, D. L., Olmschenk, S. & Monroe, C. Bell inequality violation with two remote atomic qubits. Phys. Rev. Lett. 100, 150404 (2008).
Olmschenk, S. et al. Manipulation and detection of a trapped Yb+ hyperfine qubit. Phys. Rev. A 76, 052314 (2007).
Simon, C. & Irvine, W. T. M. Robust long-distance entanglement and a loophole-free Bell test with ions and photons. Phys. Rev. Lett. 91, 110405 (2003).
Olmschenk, S. et al. Quantum teleportation between distant matter qubits. Science 323, 486–489 (2009).
Sackett, C. A. et al. Experimental entanglement of four particles. Nature 404, 256–259 (2000).
Chwalla, M. et al. Precision spectroscopy with two correlated atoms. Appl. Phys. B 89, 483–488 (2007).
Mølmer, K. & Sørensen, A. Entanglement and quantum computation with ions in thermal motion. Phys. Rev. A 62, 022311 (1999).
Lee, P. J. et al. Phase control of trapped ion quantum gates. J. Opt. B 7, S371–S383 (2005).
Inlek, I. V., Vittorini, G., Hucul, D., Crocker, C. & Monroe, C. Quantum gates with phase stability over space and time. Phys. Rev. A 90, 042316 (2014).
Schmidt, P. O. et al. Spectroscopy using quantum logic. Science 309, 749–752 (2005).
Barret, M. D. et al. Sympathetic cooling of 9Be+ and 24Mg+ for quantum logic. Phys. Rev. A 68, 042302 (2003).
Briegel, H-J., Dürr, W., Cirac, J. I. & Zoller, P. Quantum repeaters: The role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Kómár, P. et al. A quantum network of clocks. Nature Phys. 10, 582–587 (2014).
Pelc, J., Langrock, C., Zhang, Q. & Fejer, M. Influence of domain disorder on parametric noise in quasi-phase-matched quantum frequency converters. Opt. Lett. 35, 2804–2806 (2010).
Hayes, D. et al. Coherent error suppression in multiqubit entangling gates. Phys. Rev. Lett. 109, 020503 (2012).
Acknowledgements
We thank K. R. Brown, L-M. Duan, J. Kim, P. Kwiat, D. N. Matsukevich, P. Maunz, D. L. Moehring, S. Olmschenk and P. Richerme for helpful discussions. This work was supported by the Intelligence Advanced Research Projects Activity, the Army Research Office MURI Program on Hybrid Quantum Optical Circuits, and the NSF Physics Frontier Center at JQI.
Author information
Authors and Affiliations
Contributions
D.H., I.V.I., G.V., C.C., S.D., S.M.C. and C.M. all contributed to the experimental design, construction, data collection and analysis of this experiment. All authors contributed to this manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Hucul, D., Inlek, I., Vittorini, G. et al. Modular entanglement of atomic qubits using photons and phonons. Nature Phys 11, 37–42 (2015). https://doi.org/10.1038/nphys3150
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3150
This article is cited by
-
Realization of a crosstalk-avoided quantum network node using dual-type qubits of the same ion species
Nature Communications (2024)
-
Quantum networks with neutral atom processing nodes
npj Quantum Information (2023)
-
A high-fidelity quantum matter-link between ion-trap microchip modules
Nature Communications (2023)
-
Optically heralded microwave photon addition
Nature Physics (2023)
-
Noisy intermediate-scale quantum computers
Frontiers of Physics (2023)