Abstract
The newly discovered topological crystalline insulators feature a complex band structure involving multiple Dirac cones1,2,3,4,5,6, and are potentially highly tunable by external electric field, temperature or strain. Theoretically, it has been predicted that the various Dirac cones, which are offset in energy and momentum, might harbour vastly different orbital character7. However, their orbital texture, which is of immense importance in determining a variety of a material’s properties8,9,10 remains elusive. Here, we unveil the orbital texture of Pb1−xSnxSe, a prototypical topological crystalline insulator. By using Fourier-transform scanning tunnelling spectroscopy we measure the interference patterns produced by the scattering of surface-state electrons. We discover that the intensity and energy dependences of the Fourier transforms show distinct characteristics, which can be directly attributed to orbital effects. Our experiments reveal a complex band topology involving two Lifshitz transitions11 and establish the orbital nature of the Dirac bands, which could provide an alternative pathway towards future quantum applications.
Similar content being viewed by others
Main
A counterpart to charge and spin, electron orbitals are of great importance in the underlying physical processes of a variety of systems. The orbital degrees of freedom, for example, play a crucial role in the colossal magnetoresistance effect in manganese oxides, and contribute to the anisotropic electronic and magnetic properties in many other transition-metal oxide systems8. More recently, orbital ordering within the superconducting FeAs layer has been thought to govern structural phase transitions and ‘stripe’-like antiferromagnetism in Fe-based high-temperature superconductors9,10. Similarly, topological materials host complex orbital arrangements often strongly coupled to other electronic degrees of freedom12,13,14,15,16,17,18. Topological crystalline insulators (TCIs) in particular are predicted to exhibit intricate band, spin and orbital textures, potentially relevant for interactions in the quantum Hall regime. Although previous experiments provided a glimpse into the complex band topology present in TCIs (refs 3, 4, 5, 19, 20), these experimental efforts have not been able to shed light onto its orbital texture. Here we use Fourier-transform (FT) scanning tunnelling spectroscopy (STS) to reveal the distinct orbital nature of the Dirac bands in the TCI, Pb1 − xSnxSe.
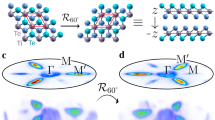
In its stoichiometric state, Pb1 − xSnxSe with x = 0 is a trivial insulator under the Z2 topological classification of materials owing to the absence of band inversion. The process of adding Sn, which substitutes for Pb, leads to band inversion at an even number of time-reversal points, and the solutions remain Z2 trivial. However, for a particular region of the composition–temperature parameter space, such as x > ∼0.23 and room temperature, or x > ∼0.18 and 4 K, topologically protected surface states emerge owing to the non-trivial band topology classified by crystalline symmetries3. Pb1 − xSnxSe crystals cleave along the (001) crystal direction based on the square lattice observed in scanning tunelling microscope (STM) topographs (Fig. 1a, b) and 3 Å step heights (Supplementary Section II). We therefore consider the band structure at the (001) face. From theory, the SS band structure consists of two ‘parent’ Dirac cones centred at X and vertically offset in energy2,21. When they intersect, the hybridization between the electron branch of the lower parent Dirac cone and the hole branch of the upper parent Dirac cone opens a gap at all points except along the mirror line, leading to the formation of a pair of ‘child’ Dirac points shifted away in momentum space from the high-symmetry point X (refs 2, 21; Fig. 1c). In addition, the SS band structure exhibits two Lifshitz transitions11 at energies EVHS+ and EVHS− where the constant energy contours (CECs) in momentum space (k-space) change from two disjointed hole pockets located symmetrically with respect to X, to one large hole pocket and a smaller electron pocket, both centred at X (Fig. 1c, d; refs 2, 21).
a, Schematic representation of the (001) surface layer consisting of two inequivalent sublattices. b, Typical scanning tunnelling microscope (STM) topograph of Pb1 − xSnxSe single crystals showing a square atomic lattice with a periodicity of ∼4.32 Å (tunnelling current (It) = 100 pA, bias voltage (Vs) = −100 mV). The black square in a,b denotes the single sublattice seen in STM topographs. c,d, Schematic of the orbital texture of the two pairs of non-identical Dirac cones (c) and band structure diagram of the surface states along the Γ–X and X–M directions within a single pair of Dirac cones (d). The orange and yellow curves in c,d indicate Sn and Se orbital character, respectively, emphasizing the different orbital texture across the Dirac point. The grey shaded area in d represents bulk bands. Different spin directions are denoted along each branch in d. e, Typical average dI/dV spectrum (red) and the distribution of dI/dV spectra (blue) acquired across a ∼30 nm square region, as described in more detail in Supplementary Section II (It = 135 pA,Vs = 59 mV).
Figure 1e shows position-dependent dI/dV spectra for this material. In general, the dI/dV spectra are V-shaped, with two well-defined peaks (Fig. 1e). From our previous studies, the minimum in the density of states of the V-shaped feature denotes the energy of the Dirac point, and the two peaks on either side represent Van Hove singularities (EVHS+/EVHS−) associated with the Lifshitz transition22. Interestingly, despite the disordered nature of our samples, with greater than 30% of the Pb sites replaced by Sn, we find that the Dirac point and the overall spectra remain homogeneous to within a few meV (Fig. 1e and also see Supplementary Section III). Having identified the important energy scales, we proceed to the application of the Fourier-transform quasiparticle interference (FT-QPI) of this system.
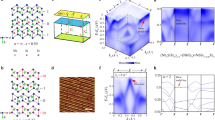
FT-QPI imaging has been successfully applied to extract the band structure of many complex systems, such as high-temperature superconductors23, heavy-fermion compounds24,25 and Z2 topological materials26,27,28, but this technique has yet to be used fully for spin- and orbital-texture mapping of extracted bands. Representative FTs of dI/dV conductance maps acquired over a 1300 Å square region of Pb0.63Sn0.37Se are shown in Fig. 2c, f. To analyse the FTs, as a starting point, the expected QPI pattern can be obtained using a simple autocorrelation of the CECs, not including any matrix element effects (Fig. 2b, e). The pattern produced can be understood by studying the Fermi surface topology shown in Fig. 2a, d. From this, we see that two main sets of scattering wavevectors (Q1/Q3 and Q2/Q4) are expected for the (001) SS. Above the Lifshitz transition, for example (Fig. 2d, e), the QPI pattern around the momentum positions Q1/Q3 originates from scattering between two (110) mirror-symmetric pairs of Dirac cones, and is expected to be quasi-elliptical. In contrast, the pattern at Q2/Q4 marks the scattering between two pairs of parent Dirac cones rotated 90 degrees with respect to one other, and should be nearly circular (Supplementary Section IV).
a,d, Schematic constant energy contours (CECs) of the TCI Pb1 − xSnxSe in the first tetragonal Brillouin zone (dashed square) at an energy close to close to Ed (a) and at an arbitrary energy higher than EVHS+ (d). Orange lines represent the surface state bands originating from four pairs of child Dirac cones (a) or parent Dirac cones (d) centred at each X point. Quasiparticle scattering occurs between different pockets and is expected to result in four principal scattering wavevectors (green arrows). b,e, Autocorrelation of CECs in a and d, respectively, showing the expected QPI signature. c,f, Fourier-transforms of dI/dV conductance maps acquired at representative energies: close to Ed (c), above EVHS+ (f). g, Energy dispersion of  in Pb0.63Sn0.37Se. The dispersion is calculated from the set of scattering wavevectors Q2 as:
in Pb0.63Sn0.37Se. The dispersion is calculated from the set of scattering wavevectors Q2 as:  , where Q2(Θ) is the angle-dependent radius of the quasi-circular feature, measured from (π/a0,π/a0) point in q-space, as outlined in Fig. 3a (Supplementary Section IV). Dashed lines in g represent linear fits to the data. Error bars in g represent the sum of errors of the Gaussian fits and the size of the smoothing window in q-space.
, where Q2(Θ) is the angle-dependent radius of the quasi-circular feature, measured from (π/a0,π/a0) point in q-space, as outlined in Fig. 3a (Supplementary Section IV). Dashed lines in g represent linear fits to the data. Error bars in g represent the sum of errors of the Gaussian fits and the size of the smoothing window in q-space.
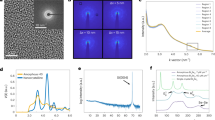
By studying the experimental FTs, our first observation is that there is a marked difference between the QPI patterns above EVHS+ (Fig. 3a), where clear, nearly circular dispersing features appear, at EVHS+ (Fig. 3b), and below EVHS+, where a (non-dispersing) ‘clover’-like set of four dots appear (Fig. 3c). This remarkable switch in the QPI pattern is directly connected to the change in Fermi surface topology across the Lifshitz transition (Fig. 3a–f). The simple autocorrelation of the CECs shown in Fig. 2b, e confirms this picture; the disconnected CECs below EVHS+ result in a non-dispersing clover pattern near Q2/Q4, whereas the continuous oval-shaped CECs above EVHS+ result in a quasi-circular dispersing pattern.
a–c, Zoom-in on the set of scattering wavevectors Q2 at energies: Ed + 122 meV, above EVHS+ (a), Ed+52 meV, at EVHS+ (b) and Ed+2 meV, below EVHS+ (c), emphasizing the striking change in the quasiparticle interference (QPI) structure across the Lifshitz transition. d–f, Schematic constant energy contour for each of the energies shown in a–c respectively. g, SS band structure along the X–Γ and X–M directions of Pb0.63Sn0.37Se. The calculated dispersion velocities along the X–Γ and X–M directions are 3.49 eV Å and 2.20 eV Å, respectively, providing the first insight into the high dispersion-anisotropy in these samples, which is determined to be 1.59. Each data point (yellow circle) was extracted solely from the dispersion of the sets of scattering wavevectors Q1 andQ2 (Supplementary Section IV). Solid orange and yellow lines in g are fits to the experimental data, extrapolated for visualization purposes assuming particle–hole symmetry. h, Average dI/dV spectrum on the same sample over the same energy range as the plot in g. Horizontal grey dashed lines across g and h denote the positions of prominent features in the spectrum (Ed, Ed2, EVHS+, EVHS−) and show an excellent match with the SS dispersion extracted from QPI. Orange and yellow lines in all panels represent Pb/Sn-like and Se-like orbital character of the states, respectively.
The main challenge of any QPI study is extracting the band structure in k-space from the observed dispersive modes in q-space. An important piece of information is provided in the set of scattering wavevectors Q2 close to the Dirac point where the clover is observed (Figs 2a–c and 3c). As the clover is a product of quasiparticle scattering between four child Dirac cones in the first Brillouin zone, the average distance in q-space between the centres of neighbouring clover leafs allows us to precisely extract the k-space distance between two Dirac cones symmetric around X to be 0.060 ± 0.006 Å−1. Interestingly, as the k-space location of the Dirac cones in TCIs is directly connected to doping19, and nominal doping is often quite different from the actual and can also vary within the sample, this method presents an alternative way to locally determine and compare the doping level in this class of materials.
To extract SS dispersion anisotropy in k-space, we need to use the q-space dispersions of the sets of wavevectors at both Q1 and Q2. Remarkably, although Q1 is expected to be weak, the high quality of our data allows us to track Q1 over a small range of energies (Supplementary Fig. 4). Using the method explained in Supplementary Section IV, we obtain the dispersions along the Γ–X and X–M directions close to the Dirac point (Fig. 3g) and determine the velocities to be vx = 3.49 eV Å and vy = 2.20 eV Å, giving an anisotropy coefficient of 1.59 and the geometric mean of velocities to be (vxvy)1/2 = 2.77 eV Å. It is important to note that no theoretical models were used to obtain these SS band dispersion velocities. Furthermore, although these velocities have been calculated without any assumptions about the exact shape of the CECs or the positions of the Lifshitz transitions, the position of the upper Lifshitz transition from Fig. 3g matches beautifully with the energy of the corresponding feature in the average dI/dV spectrum obtained on the same sample (Fig. 3h). Furthermore, the arithmetic mean of dispersion velocities (vxvy)1/2 from Landau levels in Pb1 − xSnxSe are found to be 2.60 eV Å and 2.70 eV Å for x ∼ 0.33 and x ∼ 0.30 respectively22, and are in excellent agreement with the value of 2.77 eV Å obtained from QPI dispersion in the x ∼ 0.37 sample.
Having determined the SS dispersion, we turn to one of the most striking aspects of the data, namely, the asymmetry in the intensity of the QPI pattern across Ed, which can be observed by comparing Fig. 4a, c (Supplementary Section V). As we show in the following discussion, this asymmetry is a direct consequence of the highly non-trivial orbital texture of the Dirac SS bands. The spin texture in this material can be simply stated as exhibiting left-handed chirality for the electron branches of all parent and child Dirac cones (Fig. 1d). The orbital character is, however, more complex. Whereas the two child Dirac cones are necessarily related by time-reversal symmetry and mirror symmetry, the two parent Dirac cones do not have to be similar (each of the parent Dirac cone maps to itself under either the time-reversal or mirror operator). In fact, by symmetry arguments aided by first-principles band structure computations7, the two parent Dirac cones are expected to have different orbital character and are associated with orbitals with opposite signs of mirror eigenvalues. Let us now consider the two sets of parent/child Dirac cones in k-space, one around X (π/a0, 0) and the other around Y (0, π/a0) (Fig. 1c). Theoretically, whereas the upper branch of the lower Sn parent Dirac cone is associated with pz orbital character for both X- and Y -momenta, the lower branch of the upper Se parent Dirac cone has a different orbital wavefunction—that is, Se px around X and Se py around Y (Fig. 1c). The different orbital textures below Ed at (π/a0, 0) and (0, π/a0) positions should suppress scattering between them and therefore result in diminished QPI patterns below Ed, exactly as seen in Fig. 4. Our data thus provide direct experimental confirmation of the proposed orbital arrangement of the TCI SS.
a–c, Experimentally observed Fourier-transform quasiparticle interference (FT-QPI) pattern (left half) and calculated pattern (right half) at three representative energies: above the upper Lifshitz transition (a), close to the Dirac point (b) and below the lower Lifshitz transition (c). The pattern in c shows suppressed intensity due to the orbital character of the bands, as depicted in Fig. 1. Atomic Bragg peaks are located exactly at the corners of the field of view in a–c. Insets in a–c show the constant energy contours used to generate the simulations at each energy around a single X point. d,g, Zoom-in of the set of scattering wavevectors Q2 above the upper Lifshitz transition (Ed + 122 meV) (d) and around the Dirac point energy (g). e,h, QPI signatures expected from a simple autocorrelation at the energies corresponding to d and g, respectively. e, does not show the radial asymmetry in intensity seen in the experiments in d. f,i, Simulations using the full model at the energies corresponding to d and g, respectively, showing excellent agreement. All experimental images have been 1-pixel boxcar-averaged in q-space (effectively smoothing over a radius equal to ∼0.5% of the atomic Bragg peak wavevector).
To further substantiate this picture and elucidate the origin of the specific orbital-selective scattering processes responsible for the subtle features in the QPI patterns, we use the proposed spin and orbital textures in model simulations of the QPI data. We find that the resulting simulations capture many features of our data, including changes in intensity with angle in the set of scattering wavevectors Q2 (Supplementary Section VII) that were clearly lacking in the simple autocorrelations. Take the QPI pattern at Ed + 122 meV as an example (Fig. 4d–f). The outermost high-intensity ring is due to scattering between the two Sn pz parent cones across X- and Y -neighbourhood. The inner ring comes from the scattering between the Se parent cone at one Brillouin zone corner neighbourhood and the Sn cone at the other. Without the spin- and orbital-matrix element effect (Fig. 4e), little intensity variation around the rings was found in the autocorrelation map. When the matrix element effect is turned on (Fig. 4f), the inner ring is greatly suppressed because it represents scattering between different kinds of orbitals, once again consistent with the postulated orbital texture. The intensity variation on the outer ring is in part due to the spin texture on the oval-shaped CEC and partly a consequence of the chosen impurity potential for matching the experimental data (Supplementary Section VII). We note that orbital-selective ARPES experiments16 might be able to provide further information regarding this orbital arrangement, especially within the narrow energy range between the two Lifshitz transitions (EVHS− < E < EVHS+) where a weaker QPI signature is observed.
Finally, our data show evidence for asymmetry in the dispersion velocities between the hole and electron branches of the outer Dirac cones. The dashed grey lines in Fig. 2g represent linear fits to the experimental data points and show a slight asymmetry in the slope above and below Ed. This asymmetry is also noticeable in the Landau level dispersion in the same material22 and the positions of the upper and lower Lifshitz transitions with respect to the Dirac point (Supplementary Section VI). This phenomenon could be attributed to the fact that bulk conduction and valence bands are not necessarily particle–hole symmetric29. Our observations provide strong evidence that, in addition to asymmetric nature of the orbital wavefunction, a particle–hole symmetric model with identical parent Dirac cones dispersions may not be enough to completely encompass the underlying physics present in this class of materials and that non-identical parent Dirac cones need to be taken into account.
Methods
The Pb1 − xSnxSe single crystals used for QPI imaging were grown by the self-selecting vapour growth method, cleaved at 77 K, and immediately inserted into the STM head. Doping concentration was checked using energy-dispersive X-ray spectroscopy (EDS) and electron microprobe analysis (see Supplementary Section I for more details). All dI/dV measurements were acquired at 6 K using a standard lock-in technique with ∼5 meV peak-to-peak modulation at a frequency of 1,488 Hz. We use the Lawler–Fujita drift-correction algorithm30 on all acquired data to remove the effects of slow thermal and piezoelectric drift. The quasiparticle interference (QPI) imaging technique uses the interference of elastically scattered quasiparticles (which are just electrons in this case) with different momenta k1 and k2, resulting in a standing wave ‘ripples’ of wavevector q = k1 − k2 which can be detected in STM dI/dV conductance maps. Two-dimensional FTs of dI/dV maps (FT-QPI; ref. 23) were used to extract all the scattering wavevectors.
References
Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).
Hsieh, T. H. et al. Topological crystalline insulators in the SnTe material class. Nature Commun. 3, 982 (2012).
Dziawa, P. et al. Topological crystalline insulator states in Pb1 − xSnxSe. Nature Mater. 11, 1023–1027 (2012).
Xu, S-Y. et al. Observation of a topological crystalline insulator phase and topological phase transition in Pb1 − xSnxTe. Nature Commun. 3, 1192 (2012).
Tanaka, Y. et al. Experimental realization of a topological crystalline insulator in SnTe. Nature Phys. 8, 800–803 (2012).
Slager, R-J., Mesaros, A., Juričić, V. & Zaanen, J. The space group classification of topological band-insulators. Nature Phys. 9, 98–102 (2012).
Wang, Y. J. et al. Nontrivial spin texture of the coaxial Dirac cones on the surface of topological crystalline insulator SnTe. Phys. Rev. B 87, 235317 (2013).
Tokura, Y. & Nagaosa, N. Orbital physics in transition-metal oxides. Science 288, 462–468 (2000).
Krüger, F., Kumar, S., Zaanen, J. & van den Brink, J. Spin-orbital frustrations and anomalous metallic state in iron-pnictide superconductors. Phys. Rev. B 79, 054504 (2009).
Lee, C-C., Yin, W-G. & Ku, W. Ferro-orbital order and strong magnetic anisotropy in the parent compounds of iron-pnictide superconductors. Phys. Rev. Lett. 103, 267001 (2009).
Lifshitz, I. Anomalies of electron characteristics of a metal in the high pressure region. Sov. Phys. JETP 11, 1130–1135 (1960).
Fu, L., Kane, C. & Mele, E. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X-L. & Zhang, S-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Hsieh, D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101–1105 (2009).
Cao, Y. et al. Mapping the orbital wavefunction of the surface states in three-dimensional topological insulators. Nature Phys. 9, 499–504 (2013).
Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3 . Science 325, 178–181 (2009).
Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nature Phys. 5, 398–402 (2009).
Tanaka, Y. et al. Tunability of the k-space location of the Dirac cones in the topological crystalline insulator Pb1 − xSnxTe. Phys. Rev. B 87, 155105 (2013).
Gyenis, A. et al. Quasiparticle interference on the surface of the topological crystalline insulator Pb1 − xSnxSe. Phys. Rev. B 88, 125414 (2013).
Liu, J., Duan, W. & Fu, L. Two types of surface states in topological crystalline insulators. Phys. Rev. B 88, 241303 (2013).
Okada, Y. et al. Observation of Dirac node formation and mass acquisition in a topological crystalline insulator. Science 341, 1496–1499 (2013).
Hoffman, J. E. et al. Imaging quasiparticle interference in Bi2Sr2CaCu2O8 + δ . Science 297, 1148–1151 (2002).
Zhou, B. B. et al. Visualizing nodal heavy fermion superconductivity in CeCoIn5 . Nature Phys. 9, 474–479 (2013).
Allan, M. P. et al. Imaging Cooper pairing of heavy fermions in CeCoIn5 . Nature Phys. 9, 468–473 (2013).
Seo, J. et al. Transmission of topological surface states through surface barriers. Nature 466, 343–346 (2010).
Okada, Y. et al. Direct observation of broken time-reversal symmetry on the surface of a magnetically doped topological insulator. Phys. Rev. Lett. 106, 206805 (2011).
Okada, Y. et al. Ripple-modulated electronic structure of a 3D topological insulator. Nature Commun. 3, 1158 (2012).
Dimmock, J. & Wright, G. Band edge structure of PbS, PbSe, and PbTe. Phys. Rev. 135, A821–A830 (1964).
Lawler, M. J. et al. Intra-unit-cell electronic nematicity of the high-T c copper-oxide pseudogap states. Nature 466, 347–351 (2010).
Acknowledgements
V.M. gratefully acknowledges funding from the US Department of Energy, Scanned Probe Division under Award Number DE-FG02-12ER46880 for the primary support of I.Z. and Y.O. (experiments, data analysis and writing the paper) and NSF-ECCS-1232105 for the partial support of W.Z. and D.W. (data acquisition). Work at Massachusetts Institute of Technology is supported by US Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Award DE-SC0010526 (L.F.), and NSF DMR 1104498 (M.S.). H.L. acknowledges the Singapore National Research Foundation for support under NRF Award No. NRF-NRFF2013-03. The work at Northeastern University is supported by the US Department of Energy grant number DE-FG02-07ER46352, and benefited from Northeastern University’s Advanced Scientific Computation Center (ASCC), theory support at the Advanced Light Source, Berkeley and the allocation of time at the NERSC supercomputing centre through DOE grant number DE-AC02-05CH11231. W-F.T. and C-Y.H. were supported by the NSC in Taiwan under Grant No. 102-2112-M-110-009. W-F.T. also thanks C. Fang for useful discussions. Work at Princeton University is supported by the US National Science Foundation Grant, NSF-DMR-1006492. F.C. acknowledges the support provided by MOST-Taiwan under project number NSC-102-2119-M-002-004.
Author information
Authors and Affiliations
Contributions
Y.O., I.Z. and V.M. designed the experiments. Samples were obtained from R.S., F.C. and M.Z.H. Theoretical analysis and calculations were done by C-Y.H., M.S., W-F.T., H.L., A.B. and L.F. STM experiments were carried out by Y.O., I.Z., D.W. and W.Z., I.Z., Y.O., H.L., L.F. and V.M. analysed the data and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 1397 kb)
Supplementary Movie
Supplementary Movie 1 (MP4 6649 kb)
Rights and permissions
About this article
Cite this article
Zeljkovic, I., Okada, Y., Huang, CY. et al. Mapping the unconventional orbital texture in topological crystalline insulators. Nature Phys 10, 572–577 (2014). https://doi.org/10.1038/nphys3012
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3012
This article is cited by
-
Hidden spin-orbital texture at the \(\overline{{{\Gamma }}}\)-located valence band maximum of a transition metal dichalcogenide semiconductor
Nature Communications (2022)
-
Magnetization-driven Lifshitz transition and charge-spin coupling in the kagome metal YMn6Sn6
Communications Physics (2022)
-
Probing topological quantum matter with scanning tunnelling microscopy
Nature Reviews Physics (2021)
-
Interplay of orbital effects and nanoscale strain in topological crystalline insulators
Nature Communications (2018)
-
Two-dimensional Topological Crystalline Insulator Phase in Sb/Bi Planar Honeycomb with Tunable Dirac Gap
Scientific Reports (2016)