Abstract
For more than a century, physicists have described real solids in terms of perturbations about perfect crystalline order1. Such an approach takes us only so far: a glass, another ubiquitous form of rigid matter, cannot be described in any meaningful sense as a defected crystal2. Is there an opposite extreme to a crystal—a solid with complete disorder—that forms an alternative starting point for understanding real materials? Here, we argue that the solid comprising particles with finite-ranged interactions at the jamming transition3,4,5 constitutes such a limit. It has been shown that the physics associated with this transition can be extended to interactions that are long ranged6. We demonstrate that jamming physics is not restricted to amorphous systems, but dominates the behaviour of solids with surprisingly high order. Just as the free-electron and tight-binding models represent two idealized cases from which to understand electronic structure1, we identify two extreme limits of mechanical behaviour. Thus, the physics of jamming can be set side by side with the physics of crystals to provide an organizing structure for understanding the mechanical properties of solids over the entire spectrum of disorder.
Similar content being viewed by others
Main
The jamming transition can be studied in its purest form at zero temperature in disordered packings of spheres interacting through finite-range, repulsive interactions4,5. At the transition, the packing fraction, ϕ, is just sufficient to cause unavoidable contact between particles. The marginally jammed state at this transition represents an extreme limit of solids—the epitome of disorder—in several ways. First, for a perfect crystal, the ratio of the shear to bulk modulus, G/B, is of order unity whereas for a liquid, G/B = 0 (ref. 1). At the jamming transition, the response to shear is infinitely weaker than the response to compression4. That G/B vanishes at the jamming transition implies that the marginally jammed solid lies at the extreme edge of rigidity4,5. Second, any crystalline solid supports sound modes at sufficiently low frequency; as the wavelength of sound is long enough to average over microscopic details, the crystal, even with defects, is well approximated as an elastic medium1. At the jamming transition, however, there are diverging length scales that exceed the wavelength of sound, even at arbitrarily low frequencies. This leads to qualitatively new physics: a new class of vibrational mode that overwhelms plane-wave behaviour4,5,6,7,8.
The marginally jammed solid also sits at a critical point, the jamming phase transition. This suggests that properties of this state, including the two distinguishing characteristics of vanishing G/B and a plateau in the density of states, might be reflected in systems away from the transition. For instance, although the jamming transition is inaccessible to particles with Lennard–Jones interactions, features such as the boson peak in Lennard–Jones glasses can be understood by treating the long-range attractions as a correction to jamming physics6. Similarly, numerous other studies indicate that the jamming transition influences the behaviour of systems with three-body interactions9,10,11,12,13, friction14,15,16, temperature17 and aspherical particles18,19,20. Here, we show that the physics of jamming is relevant over a surprisingly broad range of disorder. Even when a solid looks crystalline to the eye, it may nevertheless manifest mechanical properties better described by jamming than by crystalline physics.
We focus on the simplest systems that can capture both jamming and crystalline physics, namely packings of frictionless spheres of mass ms and diameter σ. Spheres i and j interact only if they overlap, in which case they feel a linear repulsive force of magnitude  , where rij is their separation. All quantities are in units of ms, σ and ε. We generate packings using an unbiased algorithm that can tune continuously between a crystal and the marginally jammed solid. We begin with N spheres arranged in a perfect crystal and introduce point defects in three ways. In variant A, we begin with N = 4,000 spheres in a face-centred cubic (fcc) lattice and introduce vacancy defects by randomly removing some fraction, m, of the spheres. The size of the box is then adjusted to obtain a desired volume fraction ϕ. The system is then relaxed to a local energy minimum using the FIRE algorithm21. Variant B is identical to A except that we begin with a body-centred cubic lattice with N = 4,394. Variant C again begins with an fcc lattice with N = 4,000 but defects are introduced as vacancy–interstitial pairs (that is, for every sphere that is removed, another is randomly inserted).
, where rij is their separation. All quantities are in units of ms, σ and ε. We generate packings using an unbiased algorithm that can tune continuously between a crystal and the marginally jammed solid. We begin with N spheres arranged in a perfect crystal and introduce point defects in three ways. In variant A, we begin with N = 4,000 spheres in a face-centred cubic (fcc) lattice and introduce vacancy defects by randomly removing some fraction, m, of the spheres. The size of the box is then adjusted to obtain a desired volume fraction ϕ. The system is then relaxed to a local energy minimum using the FIRE algorithm21. Variant B is identical to A except that we begin with a body-centred cubic lattice with N = 4,394. Variant C again begins with an fcc lattice with N = 4,000 but defects are introduced as vacancy–interstitial pairs (that is, for every sphere that is removed, another is randomly inserted).
Clearly, these algorithms generate perfect crystals when m = 0. When m = 1, variant C is identical to the algorithm commonly used for jamming5. For all variants, m ≍ 1/2 leads to configurations indistinguishable from jammed ones; thus, the two end points of all three variants coincide respectively with the perfect crystal and jamming. We adjust m and ϕ to generate states that span the two extreme cases. We then characterize the order using F6 to measure neighbour correlations of bond-orientational order22,23 (Methods). F6 = 1 for a perfect crystal and F6 ≍ 0 for a disordered system.
We study the mechanical response of packings as a function of the pressure, p. Three example zero-temperature configurations at high pressure are shown in Fig. 1a–c. The first is a slightly defected crystal with a very small density of vacancies. The second is disordered, indistinguishable from a jammed system. The third ‘intermediate’ system is structurally a defected crystal with F6 ≍ 0.9, but, as we shall see, behaves mechanically like a jammed solid. As p decreases, Fig. 1e shows that for the first two systems F6 remains constant; for the third F6 decreases but stays high, F6 > 0.75. Even as p → 0, its structure remains predominantly crystalline (Fig. 1d).
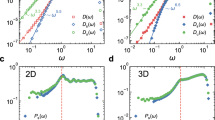
a–c, Images of three example systems generated using Variant A of our algorithm. A nearly perfect crystal with F6 = 1.0 (a), a disordered sample with F6 = 0.1 (b), and a defected crystal with F6 = 0.9 (c). Blue (red) particles have high (low) local order (see Methods). d, The same system as c after the pressure has been lowered by about seven orders of magnitude. e–g, The global order parameter F6, excess contact number Z − Ziso, and ratio of the shear modulus to bulk modulus G/B as a function of pressure for the three systems. h–j, The density of vibrational modes D(ω) for the three systems at different pressures. D(ω) for a perfect fcc crystal is provided for comparison. Note that the intermediate system, although very highly ordered, behaves in its mechanical and vibrational properties much more like the disordered sample than like the nearly perfect crystal.
For the perfect fcc crystal, each particle has exactly 12 neighbours at any p > 0. Likewise, the slightly defected crystal of Fig. 1a has an average number of contacts per particle, Z, that is independent of pressure (Fig. 1f). The disordered system of Fig. 1b decreases towards the isostatic value, Ziso ≍ 2d, as p is lowered, consistent with the well-established scaling of Z − Ziso ∼ p1/2 for jammed spheres with harmonic interactions4,5,24. Surprisingly, as the pressure is lowered in the system with intermediate order, we find that Z also approaches Ziso as a power law with roughly the same exponent. Apparently, despite the high degree of crystallinity, this system becomes marginally coordinated at low pressures.
The mechanical responses of these three systems are shown in Fig. 1g. The slightly defected crystal shows the expected response, with G/B remaining constant as p → 0, whereas for the disordered system, G/B ∼ p1/2 as expected near the jamming transition4,5. For the intermediate sample, not only is Z − Ziso similar to that of a jammed solid, but Fig. 1g shows that the mechanical properties are also more like a jammed solid than a crystalline one: G/B vanishes as p → 0 with the same power law as in jamming.
We also measure the density of normal modes of vibration, D(ω), which is directly related to the mechanical and thermal properties of the solid within the harmonic approximation25. Low-frequency modes in crystals correspond to plane waves and follow Debye scaling: D(ω) ∼ ωd − 1 (Fig. 1h). Disordered systems, in addition, possess a class of ‘anomalous’ modes that result in a low-frequency plateau in D(ω) (Fig. 1i; ref. 7), related to Z − Ziso (ref. 8). Figure 1j shows that the intermediate sample, which looks highly crystalline, has a low-frequency density of states that closely resembles that of the disordered system26.
The system in Fig. 1c indeed behaves mechanically as if it were jammed, despite its extremely ordered structure. To establish the generality of this observation, we have generated hundreds of thousands of packings with varying amounts of order, F6, using the three versions of our algorithm.
We first separate packings into bins with different degrees of order. Figure 2 shows, for different values of F6, the average of Z − Ziso and G/B versus p. Note that before averaging, packings were also binned in pressure. For the systems in Fig. 1, we lowered pressure by gradually decreasing ϕ and reminimizing energy. For the packings in Figs 2 and 3, we did not lower p but simply varied ϕ to obtain packings over a range of pressures, making it more difficult to produce low-p packings. Data are shown only for systems generated with variant A, but the other ensembles show similar features. The solid lines show the two limiting extremes corresponding to the perfect fcc crystal (blue) and jammed packings (red). At a given pressure, both Z − Ziso and G/B increase as systems become more ordered, but they retain the scaling with pressure associated with jamming, not the constant value associated with crystalline behaviour, up to relatively high values of F6. Thus, the system with intermediate order in Fig. 1c is indeed a representative example of this trend.
a, The excess contact number as a function of pressure at different values of F6 averaged over an ensemble of systems. The blue line shows the constant Z − Ziso behaviour for a perfect fcc crystal, and the red line shows the behaviour at jamming. b, The ratio of the shear modulus to bulk modulus for the same systems. Note that G/B for a perfect crystal is constant at low pressures but decreases very slightly at higher pressures. The error bars represent the standard deviations. Only for systems with very high values of F6 do the properties have the pressure independence expected for a crystal.
a, A three-dimensional plot of G/B as a function of pressure and Z − Ziso for systems with F6 < 0.75, generated with Variant A (green squares), B (orange triangles) and C (purple circles). The solid blue and red lines give the behaviour of a perfect fcc crystal and a jammed solid, respectively. b, The same data but shown from a different point of view to emphasize that all of the points lie on a well-defined plane. c, As a function of p(Z − Ziso), G/B collapses onto a single curve for all F6 < 0.75. This curve coincides with the one for jamming. The inset shows the data plotted as a function of just Z − Ziso. d, For F6 > 0.75, G/B is not cleanly described by jamming physics. The error bars in c and d represent the standard deviations. In the high F6 regime, many systems are better described as a defected crystal whereas all states with F6 < 0.75 are better described from the jamming scenario.
In jamming, the value of Z − Ziso at a given pressure is well defined. However, for our systems there is a large spread in Z − Ziso at fixed pressure. Therefore, we have binned systems according to both p and Z − Ziso and then separated them into whether they do, or do not, behave mechanically like jammed systems. The separation between these two groups of configurations in terms of F6 is not sharp: some packings with F6 > 0.95 behave like jammed ones and a few packings with F6 as low as 0.75 respond more like a crystal. This suggests that there is crossover from crystalline behaviour to jamming behaviour that occurs at remarkably high order.
To demonstrate this more clearly, Fig. 3a shows that for F6 < 0.75, G/B falls cleanly onto a single ‘jamming surface’. This includes all of the data from all three ensembles. The collapse of the data onto a single plane is made more clear in Fig. 3b, where we have rotated the point of view to look at the surface edge-on (see also Supplementary Movie 1). Figure 3c shows that the jamming surface can be scaled onto a single curve that matches the result expected for jammed packings (red line). Note that given the smoothness of the data, we can choose different scalings on the two axes and obtain a similar collapse. However, as shown by Fig. 2a and the inset in Fig. 3c, G/B is not simply a function of just p or Z − Ziso, as one might have expected. As F6 → 1, the manner in which systems approach the crystalline limit depends on the protocol—as expected, perturbations about a crystal are sensitive to the details of the perturbation. Figure 3d shows G/B averaged over all systems with F6 > 0.75. In this region there is a mixture of states that behave like crystalline configurations with those that behave like jammed packings.
It is important to understand the generality of our results. Our algorithms correspond to introducing ordinary vacancies or vacancy–interstitial pairs to an otherwise perfect crystal. As more of these simple defects are added, the mechanical behaviour changes character; at some point, the solid loses all semblance of crystalline behaviour even though its structure seems exceptionally well ordered. We have shown that in this regime the physical properties can be profitably described as perturbations about the disordered limit of a solid. Our model is also simplified because we use finite-range potentials. This choice makes the relevance of the jamming transition clear but does not limit its applicability: as emphasized above, the persistence of key features of the jamming scenario in systems with three-body interactions, friction, temperature, and aspherical particles implies that our results should be generally relevant. In particular, long-range attractions, as in Lennard–Jones systems, can be treated as merely a perturbation around a jamming description of the mechanical properties even though the jamming transition itself is not accessible6. Recently, it was suggested that hard-sphere systems below the jamming transition might have different physics27.
Of particular note, crossovers from ordered to disordered behaviour have been observed for highly crystalline systems in other contexts. When crystalline KBr is doped with KCN, the impurities form an ‘orientational glass’ without destroying the crystalline structure. The authors of ref. 28 found a crossover in the thermal conductivity from crystalline (T3) to glassy (T2) scaling when the concentration of KCN is only around 1%. Moreover, for concentrations of 25% and 50%, the specific heat and thermal conductivity seemed equally glassy. In sheared quasi-2D foams, the authors of refs 29, 30 found a crossover in the flow profile to that of disordered systems in highly ordered foams with only 2% area defects. Finally, the authors of ref. 26 showed that introducing a very slight polydispersity (0.003%) to an fcc crystal of hard spheres just below jamming causes the vibrational properties to be indistinguishable from a hard-sphere glass. It is not clear in this case if there exists a crossover to crystalline behaviour as the polydispersity is decreased, or if that limit is singular.
Our results provide a new vantage point for understanding the mechanical response of solids. Starting from the jamming scenario, we can profitably describe the behaviour of even highly ordered materials. For example, many polycrystals might be better described in terms of corrections to jamming behaviour than in terms of defected crystals. Although perfect order is a well-defined concept, it has been less clear what perfect disorder means. Our results suggest that instead of using a structural quantity such as F6, one can characterize order in terms of mechanical properties. A system behaves ordered when, for example, G/B is roughly constant in pressure and behaves disordered when it decreases with decreasing pressure. The spectrum of order in solids therefore has two well-defined limits: a perfect crystal, with constant G/B and Z − Ziso, and a perfect anti-crystal, with G/B and Z − Ziso vanishing at zero pressure.
Methods
We measure the degree of order in a given configuration by calculating the parameter F6. For each pair of neighbouring spheres i and j, the function S6(i, j) measures correlation of neighbour orientation:

where qlm(i) is the standard bond-orientational order parameter31. Summing over the Nc(i) neighbours of i, we define22,23

where Θ is the step function and  is a threshold that is typically taken to be 0.7. f6(i) measures the fraction of sphere i’s neighbours with highly correlated neighbour orientations. In a perfect crystal, f6 = 1 and in a disordered state it is small. Finally, we average f6(i) over the system to obtain a global order measure, F6.
is a threshold that is typically taken to be 0.7. f6(i) measures the fraction of sphere i’s neighbours with highly correlated neighbour orientations. In a perfect crystal, f6 = 1 and in a disordered state it is small. Finally, we average f6(i) over the system to obtain a global order measure, F6.
References
Ashcroft, N. W. & Mermin, N. D. Solid State Physics (Thomson Brooks/Cole, 1976).
Phillips, W. A. (ed.) Amorphous Solids: Low-Temperature Properties (Springer, 1981).
Liu, A. J. & Nagel, S. R. Jamming is not just cool any more. Nature 396, 21–22 (1998).
O’Hern, C. S., Silbert, L. E., Liu, A. J. & Nagel, S. R. Jamming at zero temperature and zero applied stress: The epitome of disorder. Phys. Rev. E 68, 011306 (2003).
Liu, A. J. & Nagel, S. R. The jamming transition and the marginally jammed solid. Annu. Rev. Condens. Matter Phys. 1, 347–369 (2010).
Xu, N., Wyart, M., Liu, A. J. & Nagel, S. R. Excess vibrational modes and the boson peak in model glasses. Phys. Rev. Lett. 98, 175502 (2007).
Silbert, L. E., Liu, A. J. & Nagel, S. R. Vibrations and diverging length scales near the unjamming transition. Phys. Rev. Lett. 95, 098301 (2005).
Wyart, M., Nagel, S. R. & Witten, T. A. Geometric origin of excess low-frequency vibrational modes in weakly connected amorphous solids. Europhys. Lett. 72, 486–492 (2005).
Wyart, M., Liang, H., Kabla, A. & Mahadevan, L. Elasticity of floppy and stiff random networks. Phys. Rev. Lett. 101, 215501 (2008).
Phillips, J. C. Topology of covalent non-crystalline solids I: Short-range order in chalcogenide alloys. J. Non-Cryst. Solids 34, 153–181 (1979).
Phillips, J. C. Topology of covalent non-crystalline solids II: Medium-range order in chalcogenide alloys and A Si (Ge). J. Non-Cryst. Solids 43, 37–77 (1981).
Thorpe, M. F. Continuous deformations in random networks. J. Non-Cryst. Solids 57, 355–370 (1983).
Boolchand, P., Lucovsky, G., Phillips, J. C. & Thorpe, M. F. Self-organization and the physics of glassy networks. Phil. Mag. 85, 3823–3838 (2005).
Song, C., Wang, P. & Makse, H. A. A phase diagram for jammed matter. Nature 453, 629–632 (2008).
Henkes, S., van Hecke, M. & van Saarloos, W. Critical jamming of frictional grains in the generalized isostaticity picture. Europhys. Lett. 90, 14003 (2010).
Papanikolaou, S., O’Hern, C. S. & Shattuck, M. D. Isostaticity at frictional jamming. Phys. Rev. Lett. 110, 198002 (2013).
Zhang, Z. et al. Thermal vestige of the zero-temperature jamming transition. Nature 459, 230–233 (2009).
Donev, A. et al. Improving the density of jammed disordered packings using ellipsoids. Science 303, 990–993 (2004).
Zeravcic, Z., Xu, N., Liu, A. J., Nagel, S. R. & van Saarloos, W. Excitations of ellipsoid packings near jamming. Europhys. Lett. 87, 26001 (2009).
Mailman, M., Schreck, C. F., O’Hern, C. S. & Chakraborty, B. Jamming in systems composed of frictionless ellipse-shaped particles. Phys. Rev. Lett. 102, 255501 (2009).
Bitzek, E., Koskinen, P., Gähler, F., Moseler, M. & Gumbsch, P. Structural relaxation made simple. Phys. Rev. Lett. 97, 170201 (2006).
Auer, S. & Frenkel, D. Numerical prediction of absolute crystallization rates in hard-sphere colloids. J. Chem. Phys. 120, 3015–3029 (2004).
Russo, J. & Tanaka, H. The microscopic pathway to crystallization in supercooled liquids. Sci. Rep. 2, 505 (2012).
Durian, D. J. Foam mechanics at the bubble scale. Phys. Rev. Lett. 75, 4780–4783 (1995).
Goodrich, C. P., Liu, A. J. & Nagel, S. R. Comment on ‘Repulsive contact interactions make jammed particulate systems inherently nonharmonic’. Phys. Rev. Lett. 112, 049801 (2014).
Mari, R., Krzakala, F. & Kurchan, J. Jamming versus glass transitions. Phys. Rev. Lett. 103, 025701 (2009).
Zargar, R., Russo, J., Schall, P., Tanaka, H. & Bonn, D. The Boson peak and disorder in hard sphere colloidal systems. Preprint at http://arxiv.org/abs/1403.2770 (2014).
De Yoreo, J. J. et al. Low-energy excitations in (KBr)1 − x(KCN)x in the orientational glass state. Phys. Rev. Lett. 51, 1050–1053 (1983).
Katgert, G., Möbius, M. & van Hecke, M. Rate dependence and role of disorder in linearly sheared two-dimensional foams. Phys. Rev. Lett. 101, 058301 (2008).
Katgert, G., Latka, A., Möbius, M. & van Hecke, M. Flow in linearly sheared two-dimensional foams: From bubble to bulk scale. Phys. Rev. E 79, 066318 (2009).
Steinhardt, P. J., Nelson, D. R. & Ronchetti, M. Bond-orientational order in liquids and glasses. Phys. Rev. B 28, 784–805 (1983).
Acknowledgements
We thank S. Schoenholz and D. Sussman for important discussions. This research was supported by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Awards DE-FG02-05ER46199 (A.J.L., C.P.G.) and DE-FG02-03ER46088 (S.R.N.). C.P.G. was partially supported by the NSF through a Graduate Research Fellowship.
Author information
Authors and Affiliations
Contributions
C.P.G. performed the numerical simulations. All authors designed and developed the study and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 231 kb)
Supplementary Movie
Supplementary Movie 1 (MOV 12719 kb)
Rights and permissions
About this article
Cite this article
Goodrich, C., Liu, A. & Nagel, S. Solids between the mechanical extremes of order and disorder. Nature Phys 10, 578–581 (2014). https://doi.org/10.1038/nphys3006
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3006
This article is cited by
-
From solid-like to floating: evolution of dense granular cluster in dissipation behavior
Granular Matter (2024)
-
Dissipation Behaviors of Vibrated Granular Balls in Different Gravity Environments
Microgravity Science and Technology (2024)
-
Twenty-five years of the jamming phase diagram
Nature Reviews Physics (2023)
-
Displacement Correlations in Disordered Athermal Networks
Journal of Statistical Physics (2022)
-
Failure behavior and criteria of metallic glasses
Acta Mechanica Sinica (2022)