Abstract
Superconductivity in so-called unconventional superconductors is nearly always found in the vicinity of another ordered state, such as antiferromagnetism, charge density wave (CDW), or stripe order. This suggests a fundamental connection between superconductivity and fluctuations in some other order parameter. To better understand this connection, we used high-pressure X-ray scattering to directly study the CDW order in the layered dichalcogenide TiSe2, which was previously shown to exhibit superconductivity when the CDW is suppressed by pressure1 or intercalation of Cu atoms2. We succeeded in suppressing the CDW fully to zero temperature, establishing for the first time the existence of a quantum critical point (QCP) at Pc = 5.1 ± 0.2 GPa, which is more than 1 GPa beyond the end of the superconducting region. Unexpectedly, at P = 3 GPa we observed a reentrant, weakly first order, incommensurate phase, indicating the presence of a Lifshitz tricritical point somewhere above the superconducting dome. Our study suggests that superconductivity in TiSe2 may not be connected to the QCP itself, but to the formation of CDW domain walls.
Similar content being viewed by others
Main
The term ‘unconventional superconductor’ once referred to materials whose phenomenology does not conform to the Bardeen–Cooper–Schrieffer (BCS) paradigm for superconductivity. It is now evident that, by this definition, the vast majority of known superconductors are unconventional; notable examples being the copper-oxide, iron-arsenide and iron-selenide high-temperature superconductors, heavy fermion materials such as CeIn3 and CeCoIn5, ruthenium oxides, organic superconductors, such as κ-(BEDT-TTF)2X, filled skutterudites, and so on.
Despite their diversity in structure and phenomenology, the phase diagrams of these materials all exhibit the common trait that superconductivity resides near the boundary of an ordered phase with broken translational or spin rotation symmetry. For example, superconductivity resides near antiferromagnetism in CeIn3 (ref. 3), near a spin density wave in iron arsenides4, orbital order in ruthenates5, and stripe and nematic order in the copper-oxides 6. The pervasiveness of this ‘universal phase diagram’ suggests that there exists a unifying framework—more general than BCS—in which superconductivity can be understood as coexisting with some ordered phase, potentially emerging from its fluctuations.
A classic example is the transition metal dichalcogenide family, MX2, where M = Nb, Ti, Ta, Mo, and X = Se, S, which exhibits a rich competition between superconductivity and Peierls-like charge density wave (CDW) order7. A recent, prominent case is 1T-TiSe2, which under ambient pressure has CDW order below a transition temperature TCDW = 202 K (ref. 8). This CDW phase can be suppressed either by intercalation of Cu atoms2,9, or through the application of hydrostatic pressure1,10, causing superconductivity to emerge. These studies indicate that the emergence of superconductivity coincides with a quantum critical point (QCP) at which TCDW goes to zero, suggesting that TiSe2 exemplifies the universal phenomenon of superconductivity emerging near the suppression of an ordered state. However, until now, there has been no direct observation of the QCP, impeding efforts to understand the relationship between superconductivity and the suppression of CDW order.
A better understanding of this universal relationship requires a direct study of the CDW order parameter itself, through and beyond the QCP. Such a study would define the phenomenology and set constraints on what type of theory is needed to explain this pervasive phenomenon. For this purpose, we performed X-ray scattering experiments on the CDW order in TiSe2 at low temperature and under hydrostatic pressure. Pressure is somewhat preferred to Cu doping as the former does not introduce non-stoichiometric disorder, allowing detection of quantum critical behaviour with the material nominally in its pristine state.
The origin of the CDW order in TiSe2 has been the subject of debate. Explanations for its existence range from traditional Fermi surface nesting7 to an excitonic insulator scenario11 to an indirect Jahn–Teller effect12, with the relative importance of electron–electron and electron–phonon interactions still in dispute13,14,15,16,17. What is clear is that the CDW in TiSe2 is a condensate of electron–hole pairs with nonzero total momentum, in which electron–electron interactions, the Peierls distortion and lattice pinning effects all play prominent roles.
X-ray experiments were carried out at the Cornell High Energy Synchrotron Source (CHESS) on TiSe2 crystals mounted in a screw-driven diamond anvil cell (DAC) in a closed-cycle cryostat. Experiments were done without an analyser, the detector integrating over all scattered photon energies. In this case, the experiment measures an energy-integrated, equal time correlation function, S(q), which is the Fourier transform of the time-averaged electron density correlator, incorporating both classical and quantum fluctuations18. The lowest accessible temperature was 8.3 K, which was not low enough to enter the superconducting phase but was adequate to address the energy scale of the CDW, even close to the QCP.
The signature of a CDW in TiSe2 is the existence of an order parameter reflection at a wave vector of (1/2, 1/2, 1/2), where the Miller indices (H, K, L) represent a momentum transfer q = H b1 + K b2 + L b3, where b1, b2, b3 are basis vectors of the reciprocal lattice. We note that, unlike most other dichalcogenides such as NbSe2 or TaS2, the CDW in TiSe2 at ambient pressure is always observed to be commensurate, with H, K, and L having rational values at all temperatures8,16,19, suggesting that lattice pinning plays a prominent role in its formation.
Confirming the conclusions of refs 1, 10, the CDW was found to be suppressed by hydrostatic pressure (Fig. 1a). The TCDW value fell to zero, indicating the presence of a quantum critical point at a pressure of Pc = 5.1±0.2 GPa. The pressure dependence of TCDW can be fitted well using a single power law, TCDW(P) = T |1 − P/Pc|β, where β = 0.87±0.08 is an effective exponent characterizing the observed order parameter suppression (Fig. 1c). If one assumes that a Hertz–Millis picture of quantum critical scaling applies near the QCP (refs 20, 21), this exponent β = νz, where ν is the exponent of the correlation length and z is the dynamical critical exponent. In mean field theory v = 1/2 and z = 2 for a CDW transition, implying β = 1, which is close to the measured value.
a, Scans through the charge density wave (CDW) ordering vector showing suppression of CDW correlations with increasing pressure for (H, 1/2, 1/2). b, Small, residual CDW correlations observed in the normal state, both at high and low pressure. c, Pressure-dependence of the ratio TCDW/I(0), or the Landau coupling constant g, which in McMillan’s picture is proportional to the CDW coupling constant. d, Phase boundary delineating the ordered and disordered phases in the pressure–temperature plane. The TCDW values from ref. 1 are shown for comparison (the grey dashed line is an interpolation of the data). The points were found to fit well to a single power law over the entire region, TCDW(P) = T0|1−P/Pc|β, with β = 0.87±0.08 (black dashed line), identifying the location of the quantum critical point at Pc = 5.1±0.2 GPa. Error bars on the temperature values represent the difference in reading between the cryostat cold finger and the top of the pressure cell. Error bars on the pressure values were determined by the energy resolution of the spectrometer used to monitor the ruby fluorescence lines. The range of fits consistent with these error bars were used to determine the error bars on β and Pc.
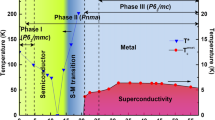
The complete phase diagram, showing the order parameter intensity, phase boundary and the location of the QCP, is shown in Fig. 2. In contrast to expectations based on refs 2, 9, 11, the QCP does not reside within the superconducting dome, which spans the range 2 GPa < P < 4 GPa, but lies more than a full GPa higher in pressure. This might seem to cast doubt on the presumed connection between CDW fluctuations and superconductivity. However, we will show below that the situation is more subtle.
a, Broad phase diagram showing charge density wave (CDW) ordered, normal state and superconducting phase boundaries. The green colour scale indicates the integrated intensity of CDW correlations, including both the C and IC components. The superconducting TSC value, reproduced from (ref. 1) has been exaggerated by a factor of five for visibility. Points where the precise commensurability was measured are labelled C, I or C/I, indicating commensurate, incommensurate or coexistence, respectively. b, Zoom-in on the region exhibiting the transition between commensurate and incommensurate order (grey dashed rectangle in a).
Surprisingly, a trace quantity of CDW correlations was observed beyond the QCP. At P = 5.9 GPa a weak, resolution-limited CDW reflection is still present, whose integrated intensity is a factor of 104 smaller than at ambient pressure. This temperature-independent feature was found to be present everywhere in the normal state of the PT phase diagram, even above the classical transition at P = 0 (Fig. 1b). This suggests that our system is experiencing a weak, uniform, symmetry-breaking field that induces a trace amount of CDW correlations in the normal state.
Near the QCP one might also expect to observe quantum critical fluctuations, which should appear as power law tails in the correlation function, that is, S(q) ∝ q−(2−η), where q is measured with respect to the ordering wave vector. However, unlike previous studies of the classical transition, in which such fluctuations are clearly visible19, no tails were observed in our study of the quantum transition, even at high momentum resolution and close to the phase boundary. We attribute this behaviour, as well as the normal state feature above, to the presence of a small, internal strain gradient in the pressure cell, which for a CDW can act as a uniform, symmetry-breaking field (further evidence for this is presented in the Supplementary Information). This field prevents systematic study of the fluctuations. However, a great deal can still be learned from the behaviour of the order parameter itself.
Just as TCDW is suppressed by pressure, so too is the low-temperature value of the CDW integrated intensity, I(0). This may provide insight into the pressure dependence of the interactions that drive the CDW. The CDW in TiSe2 is believed to be rather strongly coupled, with 2Δ ≍ 7kBTCDW (ref. 7) and a normal state coherence length, ξ0, of just a few lattice parameters17. It was argued by McMillan22 that, in this case, the ratio TCDW/I(0) is proportional to the Landau coupling constant, g, which we plot in Fig. 1c. Although one might expect the coupling strength to decrease as the phase transition is approached, the trend in the ratio is the opposite, rising continuously up to P = Pc. McMillan’s mean field expression, which applies only to the ordered side of the transition where TCDW is nonzero, neglects disorder and quantum fluctuations and is too simplistic to accurately describe the region close to the QCP. Nonetheless, Fig. 1c suggests that the suppression of the CDW arises from some effect other than reduction in the coupling constant, such as changes in the commensurability or lattice stiffness23.
To investigate this possibility, we employed a novel, precision technique for measuring the degree of commensurability of the CDW. The difficulty in such a measurement is referencing the wave vector of the CDW to a Bragg reflection of the underlying lattice. In the case of TiSe2, there is no Bragg reflection close to the CDW, so any small geometric misalignment propagates into large errors in the values of (H, K, L).
To overcome this difficulty, we performed scattering experiments at two photon energies simultaneously. An X-ray source with diffractive optics always contains harmonics, that is, a small percentage of photons with precisely half the wavelength, in our case a tiny fraction of 36 keV photons in our nominally 18 keV beam. Rather than filtering out the harmonics, we employed an energy-proportional detector to measure both energies in parallel, allowing simultaneous measurement of the (H, K, L) and (2H, 2K, 2L) points in momentum space. This allowed us to reference in situ the CDW correlations near (1/2, 1/2, 1/2) to the Bragg reflection at (1, 1, 1), eliminating errors due to misalignment, temperature drifts and so on. This measurement was performed at a selection of points across the phase diagram, at pressures near and below the superconducting dome. The results are summarized in Fig. 3, with labels ‘C’ or ‘IC’ added to the corresponding points in Fig. 2.
Blue curves correspond to the fundamental, charge density wave signal near (0.5, 0.5, 0.5), and grey curves show scattering from the harmonic due to the (1, 1, 1) Bragg reflection at double the momentum. The bars indicate errors from Poisson counting statistics, that is,  . At P = 1.9 GPa (left) the fundamental and harmonic curves always coincide, even up to the phase boundary at T = 160 K. However at P = 3 GPa (left), above the superconducting dome, the curves separate above 25 K, indicating a transition to incommensurate behaviour. All scans are plotted against the z-component of the momentum, L, which is the direction of largest incommensurability.
. At P = 1.9 GPa (left) the fundamental and harmonic curves always coincide, even up to the phase boundary at T = 160 K. However at P = 3 GPa (left), above the superconducting dome, the curves separate above 25 K, indicating a transition to incommensurate behaviour. All scans are plotted against the z-component of the momentum, L, which is the direction of largest incommensurability.
Consistent with past X-ray studies8, at low pressures the CDW was found to be commensurate to within the experimental resolution of a few thousandths of a reciprocal lattice unit (r.l.u.). This was true even for the anomalous normal state peak observed above TCDW (Fig. 1b). Surprisingly, however, at P = 3 GPa—directly above the superconducting dome—weak incommensurate behaviour was observed at the level of 2 × 10−3 r.l.u. At the lowest temperatures the CDW is commensurate, but IC behaviour emerged as the temperature was increased, becoming most pronounced near the phase boundary at T = 90 K. The incommensurability was largest along the L direction (Fig. 3), suggesting that the IC behaviour may be attributed to phase slips in the stacking of the CDW order along the c axis, separated by a distance ∼1/0.002 = 500 lattice parameters. Although it was not possible to perform this measurement at every point in the phase diagram, observation of IC behaviour is sufficient to establish the existence of a Lifshitz multicritical point, analogous to behaviour in helical ferromagnets24, somewhere in the region above the superconductivity dome.
The transition from C to IC CDW order may be weakly first order. Although the effect lies near the limit of our resolution, the transition appears to exhibit a coexistence region for 25 K < T < 50 K, in which both C and IC phases are present (Fig. 3). A first-order character would make this C/IC transition similar to those in other dichalcogenides, such as 1T-TaSe2 (ref. 25) and 1T-TaS2 (ref. 26).
Our study has significant bearing on the existing picture of CDW melting and the emergence of superconductivity in TiSe2. First, the existence of an IC phase suggests that the natural wave vector of the CDW, which is set by the Fermi surface topology, shifts from the commensurate point as the energy bands adjust with pressure. This destabilizes the CDW by reducing the energy saved from the lattice pinning potential. We note that this view is not dependent on a Fermi surface nesting picture of the CDW, as the wave vectors of strong coupling phases, such as the excitonic insulator, are also determined by the band topology7.
Next, the separation of superconductivity and the QCP by more than 1 GPa suggests that superconductivity in TiSe2 is not directly associated with the vanishing of the CDW itself. Instead, we find that the superconductivity region coincides with a commensurate–incommensurate transition, at which the CDW order acquires a dilute concentration of phase slips. This suggests that the onset of superconductivity in TiSe2 is associated with the formation of domain walls in the CDW order, rather than the amplitude QCP itself. To the extent that TiSe2 typifies other materials exhibiting the universal phase diagram, our study suggests a fundamental connection between unconventional superconductivity and the quantum dynamics of domain walls. We note that a similar connection between phase fluctuations of charge-ordered domains and superconductivity has been inferred in studies of copper-oxides27,28.
Methods
Sample preparation.
1T-TiSe2 single crystals were grown by means of an iodine vapour transport technique. Ti powder and slight excesses of Se powder were loaded in a vacuum sealed quartz tube along with a small amount of iodine. The tube was heated to 570–640 °C for 6 h, maintained in a temperature gradient for a week, and cooled to room temperature over 12 h.
Hydrostatic pressure.
A Bell–Mao-type, screw-driven diamond anvil cell was used to generate hydrostatic pressure. A 4:1 volumetric methanol–ethanol mixture was used as a pressure-transmitting medium. This mixture was chosen because it retains hydrostaticity up to 10 GPa. A 400 μm thick copper gasket was pre-indented down to 230 μm and drilled for the sample chamber, which was about 450 μm in diameter. The pressure was calibrated by measuring the fluorescence of a small ruby chip placed in the sample beside the TiSe2 crystal.
X-ray experiments.
Experiments were carried out at the C1 beam line at CHESS with a 4 K displex installed on a four-circle diffractometer. To simultaneously measure scattering at (0.5, 0.5, 0.5) and (1, 1, 1), an energy-proportional scintillation counter was fed into two independent single-channel analysers to bin the 18 keV and 36 keV photons into separate scaler channels.
References
Kusmartseva, A. F., Sipos, B., Berger, H., Forró, L. & Tutiš, E. Pressure induced superconductivity in 1T-TiSe2 . Phys. Rev. Lett. 103, 236401 (2009).
Morosan, E. et al. Superconductivity in CuxTiSe2 . Nature Phys. 2, 544–550 (2006).
Mathur, N. D. et al. Magnetically mediated superconductivity in heavy fermion compounds. Nature 394, 39–43 (1998).
Canfield, P. C. & Bud’ko, S. L. FeAs-based superconductivity: A case study of the effects of transition metal doping on BaFe2As2 . Ann. Rev. Cond. Matter Phys. 1, 27–50 (2010).
Nakatsuji, S. & Maeno, Y. Quasi-two-dimensional Mott transition system Ca2 − xSrxRuO4 . Phys. Rev. Lett. 84, 2666–2669 (2000).
Tranquada, J. M., Sternlieb, B. J., Axe, J. D., Nakamura, Y. & Uchida, S. Evidence for stripe correlations of spins and holes in copper-oxide superconductors. Nature 375, 561–563 (1995).
Rossnagel, K. On the origin of charge density waves in select layered transition-metal dichalcogenides. J. Phys. Condens. Matter 23, 213001 (2011).
DiSalvo, F. J., Moncton, D. E. & Waszczak, J. V. Electronic properties and superlattice formation in the semimetal TiSe2 . Phys. Rev. B 14, 4321–4328 (1976).
Barath, H. et al. Quantum and classical mode softening near the charge-density-wave/superconductor transition of CuxTiSe2 . Phys. Rev. Lett. 100, 106402 (2008).
Snow, C. S., Karpus, J. F., Cooper, S. L., Kidd, T. E. & Chiang, T-C. Quantum melting of the charge-density-wave state in 1T-TiSe2 . Phys. Rev. Lett. 91, 136402 (2003).
May, M. M., Brabetz, C., Janowitz, C. & Manzke, R. Charge-density-wave phase of 1T-TiSe2: The influence of conduction band population. Phys. Rev. Lett. 107, 176405 (2011).
Kidd, T. E., Miller, T., Chou, M. Y. & Chiang, T-C. Electron–hole coupling and the charge density wave transition in TiSe2 . Phys. Rev. Lett. 88, 226402 (2002).
Van Wezel, J., Nahai-Williamson, P. & Saxena, S. S. Exciton-phonon-driven charge density wave in TiSe2 . Phys. Rev B 81, 165109 (2010).
Monney, C., Battaglia, C., Cercellier, H., Aebi, P. & Beck, H. Exciton condensation driving the periodic lattice distortion of 1T-TiSe2 . Phys. Rev. Lett. 106, 106404 (2011).
Hellmann, S. et al. Time-domain classification of charge-density-wave insulators. Nature Commun. 3, 1039 (2012).
Castellan, J-P. et al. Chiral phase transition in charge-ordered 1T-TiSe2 . Phys. Rev. Lett. 110, 196404 (2013).
Weber, F. et al. Electron–phonon coupling and the soft phonon mode in TiSe2 . Phys. Rev. Lett. 107, 266401 (2011).
Abbamonte, P. et al. Ultrafast imaging and the phase problem for inelastic X-ray scattering. Adv. Mater. 22, 1141–1147 (2010).
Holt, M., Zschack, P., Hong, H., Chou, M. Y. & Chiang, T-C. X-ray studies of phonon softening in TiSe2 . Phys. Rev. Lett. 86, 3799–3802 (2001).
Hertz, J. A. Quantum critical phenomena. Phys. Rev. B 14, 1165–1184 (1976).
Millis, A. J. Effect of nonzero temperature on quantum critical points in itinerant fermion systems. Phys. Rev. B 48, 7183–7196 (1993).
McMillan, W. L. Microscopic model of charge-density waves in 2H-TaSe2 . Phys. Rev. B 16, 643–650 (1977).
Calandra, M. & Mauri, F. Charge-density wave and superconducting dome in TiSe2 from electron–phonon interaction. Phys. Rev. Lett. 106, 196406 (2011).
Hornreich, R. M. The Lifshitz point: Phase diagrams and critical behavior. J. Magn. Magn. Mater. 15-18, 387–392 (1980).
Moncton, D. E., Axe, J. D. & DiSalvo, F. J. Study of superlattice formation in 2H-NbSe2 and 2H-TaSe2 by neutron scattering. Phys. Rev. Lett. 34, 734 (1975).
Sipos, B. et al. From Mott state to superconductivity in 1T-TaS2 . Nature Mater. 7, 960–965 (2008).
Fradkin, E. & Kivelson, S. A. High-temperature superconductivity: Ineluctable complexity. Nature Phys. 8, 864–866 (2012).
Mesaros, A. et al. Topological defects coupling smectic modulations to intra-unit-cell nematicity in cuprates. Science 333, 426–430 (2011).
Acknowledgements
We gratefully acknowledge discussions with P. B. Littlewood, M. R. Norman, R. Osborn and W-C. Lee. High-pressure X-ray experiments were supported by the US Department of Energy under grant No. DE-FG02-06ER46285. Crystal growth was supported by DOE grant No. DE-FG02-07ER46453. Use of the CHESS was supported by the National Science Foundation and the National Institutes of Health/National Institute of General Medical Sciences under NSF award DMR-0936384. T.C.C. was supported by DOE grant No. DE-FG02-07ER46383.
Author information
Authors and Affiliations
Contributions
Y.I.J. and P.A. designed the experiment. Y.I.J., K.D.F. and P.A. built the experimental apparatus. Y.I.J., X.M.C., K.D.F., G.A.P., Y.G., J.C.T.L., J.G. and P.A. performed the X-ray experiments. S.Y., Y.I.J. and S.L.C. grew the crystals. Y.I.J., P.G., G.J.M., S.L.C., T.C.C., E.F. and P.A. analysed and interpreted the data. P.A. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 1337 kb)
Rights and permissions
About this article
Cite this article
Joe, Y., Chen, X., Ghaemi, P. et al. Emergence of charge density wave domain walls above the superconducting dome in 1T-TiSe2. Nature Phys 10, 421–425 (2014). https://doi.org/10.1038/nphys2935
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2935
This article is cited by
-
Endotaxial stabilization of 2D charge density waves with long-range order
Nature Communications (2024)
-
Topotactic fabrication of transition metal dichalcogenide superconducting nanocircuits
Nature Communications (2023)
-
Electron-momentum dependence of electron-phonon coupling underlies dramatic phonon renormalization in YNi2B2C
Nature Communications (2022)
-
Revealing the order parameter dynamics of 1T-TiSe\(_2\) following optical excitation
Scientific Reports (2022)
-
Real-space anisotropy of the superconducting gap in the charge-density wave material 2H-NbSe2
npj Quantum Materials (2022)