Abstract
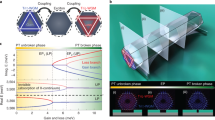
Optical systems combining balanced loss and gain provide a unique platform to implement classical analogues of quantum systems described by non-Hermitian parity–time (PT)-symmetric Hamiltonians. Such systems can be used to create synthetic materials with properties that cannot be attained in materials having only loss or only gain. Here we report PT-symmetry breaking in coupled optical resonators. We observed non-reciprocity in the PT-symmetry-breaking phase due to strong field localization, which significantly enhances nonlinearity. In the linear regime, light transmission is reciprocal regardless of whether the symmetry is broken or unbroken. We show that in one direction there is a complete absence of resonance peaks whereas in the other direction the transmission is resonantly enhanced, a feature directly associated with the use of resonant structures. Our results could lead to a new generation of synthetic optical systems enabling on-chip manipulation and control of light propagation.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Boettcher, S. & Bender, C. M. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 80, 5243–5246 (1998).
Bender, C. M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 70, 947–1018 (2007).
Mostafazadeh, A. Pseudo-Hermiticity versus PT symmetry: the necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian. J. Math. Phys. 43, 205–214 (2002).
Guo, A. et al. Observation of PT-symmetry breaking in complex optical potentials. Phys. Rev. Lett. 103, 093902 (2009).
Rüter, C. E. et al. Observation of parity–time symmetry in optics. Nature Phys. 6, 192–195 (2010).
Feng, L. et al. Nonreciprocal light propagation in a silicon photonic circuit. Science 333, 729–733 (2011).
Regensburger, A. et al. Parity–time synthetic photonic lattices. Nature 488, 167–171 (2012).
Feng, L. et al. Experimental demonstration of a unidirectional reflectionless parity–time metamaterial at optical frequencies. Nature Mater. 12, 108–113 (2012).
Schindler, J., Li, A., Zheng, M. C., Ellis, F. M. & Kottos, T. Experimental study of active LRC circuits with PT symmetries. Phys. Rev. A 84, 040101(R) (2011).
Zheng, C., Hao, L. & Long, G. L. Observation of fast evolution in parity–time-symmetric system. Phil. Trans. R. Soc. A 371, 20120053 (2013).
Bittner, S. et al. PT symmetry and spontaneous symmetry breaking in a microwave billiard. Phys. Rev. Lett. 108, 024101 (2012).
Bender, C. M., Berntson, B. K., Parker, D. & Samuel, E. Observation of PT phase transition in a simple mechanical system. Am. J. Phys. 81, 173–179 (2013).
Bender, N. et al. Observation of asymmetric transport in structures with active nonlinearities. Phys. Rev. Lett. 110, 234101 (2013).
Chtchelkatchev, N. M., Golubov, A. A., Baturina, T. I. & Vinokur, V. M. Stimulation of the fluctuation superconductivity by PT symmetry. Phys. Rev. Lett. 109, 150405 (2012).
Sukhorukov, A. A., Xu, Z. & Kivshar, Y. S. Nonlinear suppression of time reversals in PT-symmetric optical couplers. Phys. Rev. A 82, 043818 (2010).
Ramezani, H., Kottos, T., El-Ganainy, R. & Christodoulides, D. N. Unidirectional nonlinear PT-symmetric optical structures. Phys. Rev. A 82, 043803 (2010).
Lin, Z. et al. Unidirectional invisibility induced by PT-symmetric periodic structures. Phys. Rev. Lett. 106, 213901 (2011).
Longhi, S. Invisibility in PT-symmetric complex crystals. J. Phys. A 44, 485302 (2011).
Jones, H. F. Analytic results for a PT-symmetric optical structure. J. Phys. A 45, 135306 (2012).
Zhu, X., Feng, L., Zhang, P., Yin, X. & Zhang, X. One-way invisible cloak using parity–time symmetric transformation optics. Opt. Lett. 38, 2821–2824 (2013).
Hang, C., Huang, G. & Konotop, V. V. PT symmetry with a system of three-level atoms. Phys. Rev. Lett. 110, 083604 (2013).
Graefe, E-M. Stationary states of a PT symmetric two-mode Bose-Einstein condensate. J. Phys. A 45, 444015 (2012).
Agarwal, G. S. & Qu, K. Spontaneous generation of photons in transmission of quantum fields in PT-symmetric optical systems. Phys. Rev. A 85, 031802 (2012).
Benisty, H. et al. Implementation of PT symmetric devices using plasmonics: principle and applications. Opt. Exp. 19, 18004 (2011).
Lazarides, N. & Tsironis, G. P. Gain-driven discrete breathers in PT-symmetric nonlinear metamaterials. Phys. Rev. Lett. 110, 053901 (2013).
Yin, X. & Zhang, X. Unidirectional light propagation at exceptional points. Nature Mater. 12, 175–177 (2013).
Fan, S. et al. Comment on nonreciprocal light propagation in a silicon photonic circuit. Science 335, 38 (2012).
Chong, Y. D., Ge, L., Cao, H. & Stone, A. D. Coherent perfect absorbers: Time-reversed lasers. Phys. Rev. Lett. 105, 053901 (2010).
Longhi, S. PT-symmetric laser absorber. Phys. Rev. A 82, 031801(R) (2010).
Chong, Y. D., Ge, L. & Stone, A. D. PT-symmetry breaking and laser-absorber modes in optical scattering systems. Phys. Rev. Lett. 106, 093902 (2011).
Liang, G. Q. & Chong, Y. D. Optical resonator analog of a two-dimensional topological insulator. Phys. Rev. Lett. 110, 203904 (2013).
Liertzer, M. et al. Pump-induced exceptional points in lasers. Phys. Rev. Lett. 108, 173901 (2012).
Yu, Z. & Fan, S. Complete optical isolation created by indirect interband photonic transitions. Nature Photon. 3, 91–94 (2009).
Gallo, K., Assanto, G., Parameswaran, K. R. & Fejer, M. M. All-optical diode in a periodically poled lithium niobate waveguide. Appl. Phys. Lett. 79, 314–316 (2001).
Kang, M. S., Butsch, A. & Russell, P. St. J. Reconfigurable light-driven opto-acoustic isolators in photonic crystal fibre. Nature Photon. 5, 549–553 (2011).
Bi, L. et al. On-chip optical isolation in monolithically integrated non-reciprocal optical resonators. Nature Photon. 5, 758–762 (2011).
Fan, L. et al. An all-silicon passive optical diode. Science 335, 447–450 (2012).
Lira, H., Yu, Z., Fan, S. & Lipson, M. Electrically driven nonreciprocity induced by interband photonic transition on a silicon chip. Phys. Rev. Lett. 109, 033901 (2012).
Vahala, K. J. Optical microcavities. Nature 106, 839–846 (2003).
Armani, D. K., Kippenberg, T. J., Spillane, S. M. & Vahala, K. J. Ultra-high-Q toroid microcavity on a chip. Nature 421, 925–928 (2003).
Yang, L., Carmon, T., Min, B., Spillane, S. M. & Vahala, K. J. Erbium-doped and Raman microlasers on a silicon chip fabricated by the sol-gel process. Appl. Phys. Lett. 86, 091114 (2005).
He, L., Ozdemir, S. K. & Yang, L. Whispering gallery microcavity lasers. Laser Photon. Rev. 7, 60–82 (2013).
Peng, B., Ozdemir, S. K., Zhu, J., Zhu, & Yang, L. Photonic molecules formed by coupled hybrid resonators. Opt. Lett. 37, 3435–3437 (2012).
Bender, C. M., Gianfreda, M., Ozdemir, S. K., Peng, B. & Yang, L. Twofold transition in PT-symmetric coupled oscillators. Phys. Rev. A 88, 062111 (2013).
Benisty, H., Yan, C., Degiron, A. & Lupu, A. T. Healing near-PT-symmetric structures to restore their characteristic singularities: Analysis and examples. J. Lightwave Technol. 30, 2675–2683 (2012).
He, L., Ozdemir, S. K., Zhu, J., Kim, W. & Yang, L. Detecting single viruses and nanoparticles using whispering gallery microlasers. Nature Nanotech. 6, 428–432 (2011).
Zhu, J. et al. Single nanoparticle detection and sizing by mode-splitting in an ultra-high-Q microtoroid resonator. Nature Photon. 4, 46–49 (2010).
Dantham, V. R. et al. Label-free detection of single protein using a nanoplasmonic-photonic hybrid microcavity. Nano Lett. 13, 3347–3351 (2013).
Ozdemir, S. K., Zhu, J., He, L. & Yang, L. Estimation of Purcell factor from mode-splitting spectra in an optical microcavity. Phys. Rev. A 83, 033817 (2011).
Bumki, M. et al. High-Q surface-plasmon-polariton whispering-gallery microcavity. Nature 457, 455–458 (2009).
Kippenberg, T. J. & Vahala, K. J. Cavity optomechanics: Back-action at the mesoscale. Science 321, 1172–1176 (2008).
Aoki, T. et al. Observation of strong coupling between one atom and a monolithic microresonator. Nature 442, 671–674 (2006).
Acknowledgements
This work is supported by Army Research Office grant No. W911NF-12-1-0026. C.M.B. is supported by US Department of Energy grant No. DE-FG02-91ER40628. F.N. is partially supported by the RIKEN iTHES Project, MURI Center for Dynamic Magneto-Optics, Grant-in-Aid for Scientific Research (S), MEXT Kakenhi on Quantum Cybernetics and the JSPS through its FIRST program. F.L. and G.L.L. are supported by the National Natural Science Foundation of China (Grant Nos 11175094, 91221205), the National Basic Research Program of China (Grant No. 2011CB921602), and the Collaborative Innovation Center of Quantum Matter, Beijing, China.
Author information
Authors and Affiliations
Contributions
S.K.O. and L.Y. conceived the idea and designed the experiments; B.P. performed the experiments with help from F.L., F.M. and S.K.O. Theoretical background and simulations were provided by F.L., F.M., M.G., C.M.B., S.F. and F.N. All authors discussed the results, and S.K.O. and L.Y. wrote the manuscript with inputs from all authors. L.Y. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 2923 kb)
Rights and permissions
About this article
Cite this article
Peng, B., Özdemir, Ş., Lei, F. et al. Parity–time-symmetric whispering-gallery microcavities. Nature Phys 10, 394–398 (2014). https://doi.org/10.1038/nphys2927
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2927
This article is cited by
-
Machine learning for knowledge acquisition and accelerated inverse-design for non-Hermitian systems
Communications Physics (2023)
-
Spontaneous symmetry breaking and ghost states in two-dimensional fractional nonlinear media with non-Hermitian potential
Communications Physics (2023)
-
Defect modes in defective one dimensional parity-time symmetric photonic crystal
Scientific Reports (2023)
-
Dynamically crossing diabolic points while encircling exceptional curves: A programmable symmetric-asymmetric multimode switch
Nature Communications (2023)
-
Noiseless single-photon isolator at room temperature
Communications Physics (2023)