Abstract
The experimental search for magnetic monopole particles1,2,3 has, so far, been in vain. Nevertheless, these elusive particles of magnetic charge have fuelled a rich field of theoretical study4,5,6,7,8,9,10. Here, we created an approximation of a magnetic monopole in free space at the end of a long, nanoscopically thin magnetic needle11. We experimentally demonstrate that the interaction of this approximate magnetic monopole field with a beam of electrons produces an electron vortex state, as theoretically predicted for a true magnetic monopole3,11,12,13,14,15,16,17,18. This fundamental quantum mechanical scattering experiment is independent of the speed of the electrons and has consequences for all situations where electrons meet such monopole magnetic fields, as, for example, in solids. The set-up not only shows an attractive way to produce electron vortex states but also provides a unique insight into monopole fields and shows that electron vortices might well occur in unexplored solid-state physics situations.
Similar content being viewed by others
Main
Magnetic monopoles have provided a rich field of study, leading to a wide area of research in particle physics4,5,6, solid-state physics7, ultra-cold gases8, superconductors9, cosmology4 and gauge theory10. As electric charges can be seen as monopole sources and sinks of electric field lines, the strong symmetry with magnetic and electrical fields for example in the free-space Maxwell equations19,20,21 hints at the possible existence of magnetic monopoles as well. So far, the search for such magnetic monopoles has been unsuccessful. However, an effective monopole field can be produced at the tip of a nanoscopic magnetized ferromagnetic needle11,17. The Aharanov–Bohm effect12 can be used to understand the effects of such a monopole field on its surroundings, which is crucial to its observation and provides a better grasp of fundamental physical theory. Previous studies have been limited to theoretical semiclassical optical calculations of the motion of electrons in such a monopole field13. Solid-state systems such as the recently studied ‘spin ice’ provide a constrained system to study similar fields, but make it impossible to separate the monopole from the material7. Here, we realize the diffraction of fast electrons on the magnetic monopole field generated by the extremity of a long magnetic needle. Free-space propagation of the electrons helps in the understanding of the dynamics of the electron–monopole system without the complexity of a solid-state system and will allow various areas of physics to use the effects of monopole fields. Various predictions about angular momentum, paths of travel and general field effects can readily be studied using the available equipment. The experiment performed here shows that even without a true magnetic monopole particle, the theoretical background on monopoles serves as a basis for experiments.
Indeed, it has been predicted that when a plane electron wave interacts with a hypothetical magnetic monopole, a vortex electron state Ψout would arise3,11,12,13,14,15,16,17,18:

with m depending on the charge of the magnetic monopole and ϕ being the azimuthal angle in the plane perpendicular to the electron wave propagation.
Approximating the magnetic monopole now by the end of a magnetic needle leads to similar effects. Indeed, such a semi-infinite cylinder of magnetic flux has been considered in earlier work on magnetic monopoles but has remained a thought experiment so far22. From the description of the monopole field by a vector potential, a flux line, or ‘Dirac string’ arises as a mathematical pathology that should be undetectable if a magnetic monopole was to be a true monopole, leading to the famous magnetic charge quantization1.
The magnetic vector potential A is a mathematical tool used in quantum physics that has real, measurable effects12 that were experimentally demonstrated by electron diffraction18,23. The Aharonov–Bohm (AB) phase is acquired by an electron when its path encloses magnetic flux:

with ds being an infinitesimal part of the trajectory. This phase is a purely quantum mechanical effect as it is present even if the electron does not cross a region containing magnetic flux, a case where classical forces have no influence on the passing electrons. The Aharonov–Bohm effect is most often discussed with infinite cylinders of magnetic flux, avoiding the interesting end points where the magnetic field B = rotA takes the form of a monopole:

with r being a radial vector of length r originating from the end point of the cylinder. If one calculates the Aharonov–Bohm phase for electrons perpedicularly passing by a semi-infinite cylinder of flux, one obtains a linear azimuthal dependency around the end point of the cylinder24:

This means that a passing electron will indeed be transformed into a vortex state. For a true monopole field, where the charge g is quantized, this leads to an integer m (g = mℏc/(2e)), resulting in a perfect phase vortex of topological charge m. There are several different derivations of this phase factor, all extensively discussed in the literature, and all predicting the same vortex phase factor3,22,24. A sketch and discussion on the subtle differences between the effect of a semi-infinite cylinder of flux and a true monopole is given in Supplementary Fig. 8.
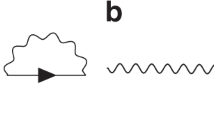
Carefully tuning a magnetic needle leads to the same phase structure, which is indistinguishable from a true monopole as long as the needle is thin and the flux converges towards a quantized flux. Here, we successfully produced an approximation to a Dirac string with a nanoscopic magnetized ferromagnetic needle. The interaction of a plane electron wave with only one end of the needle enables the typical azimuthal Aharonov–Bohm phase shift to occur and vortex electron states to be created, as sketched in Fig. 1a.
a, An incoming electron plane wave is transformed into a vortex beam with a helical wavefront, through interaction with the magnetic monopole field (orange lines with arrows). b, Scanning electron micrograph view of the experimental design. The nickel needle and its copper base are soldered to a gold-plated SiN aperture using FIB-assisted Pt deposition. Half of the Ni needle is positioned over a 20-μm circular aperture, forming a local monopole field.
The needle is extracted from bulk Ni making use of a focused ion beam (FIB) instrument, resulting in a cone approximating an elongated cylinder with a cone angle of about 2° shown in Fig. 1b. The strong shape anisotropy between the needle length (21.4 μm) and the tip diameter of only 200 nm leads to a situation where only a single on-axis magnetic domain occurs. After shaping the needle, it is positioned over a 20 μm circular aperture drilled in a non-magnetic Au-coated thin SiN film, to make sure electrons can interact with only one end of the needle and its magnetic monopole field.
We can verify the magnetic state at the tip of the nickel needle (red square in Fig. 2a) by inserting it in a transmission electron microscope (TEM) and performing electron holography in field-free conditions11,18, sketched in Supplementary Fig. 1. This method measures the Aharanov–Bohm phase shift of the electrons caused by the magnetic vector potential around the needle. The resulting experimental phase map is shown in Fig. 2b and reveals the typical spiraling character in qualitative agreement with a finite element simulation for the same shape given in Fig. 2c and Supplementary Fig. 2. The phase image resembles that of optical spiral phase plates, as used to create optical vortices25. Exposing the needle to an external on-axis magnetic field flips the axis of magnetization without going through multi domain states (Supplementary Fig. 3). When the magnetization direction is reversed, the handedness of the phase reverses as expected (Supplementary Fig. 3). In this sense, the needle tip behaves as a magnetic monopole with a polarity that can be chosen depending on the magnetization direction.
a, Magnified scanning electron micrograph of the needle positioned onto the circular aperture. The red dashed square region indicates the position of images b and c. b, Experimental phase map caused by the magnetic field around the Ni needle obtained by electron holography in field-free conditions. The phase map is drawn in three dimensions to emphasize its helicity. c, Finite element simulation of the phase map around a modelled needle. Detailed phase profiles are supplied in Supplementary Fig. 4.
Illuminating the needle with a plane electron wave (300 kV, λ = 1.97 pm) inside a TEM allows experimental verification of whether a magnetic monopole field creates a vortex electron state. A series of images is recorded in the far field at different defocus of an imaging lens showing, in Fig. 3a, the presence of a central dark region. This persistent area of destructive interference is a clear sign of a phase discontinuity in the centre, as expected for vortex waves. The ring is not exactly closed, which occurs when a non-integer orbital angular momentum (OAM) is present26. Decomposing the phase map over the full aperture for the simulated magnetized needle into OAM eigenmodes indeed indicates that the deviation from a pure cylindrical shape leads to a distribution of OAM eigenmodes with an average of −5.8ℏ per electron (Supplementary Fig. 5). These experimental observations agree remarkably well with wave optical simulations presented in Fig. 3b ruling out the possibility that the dark region is caused by a shadowing effect (see Supplementary Fig. 6 for further simulations).
a, Through-focus series of the needle aperture in the diffraction plane. Note the persistent dark region in the centre caused by destructive interference typical for vortex waves. The near-focus central image shows a doughnut-like intensity profile, typical of a vortex beam that opens on one side and indicating a non-integer total orbital angular momentum. b, Wave optical simulation obtained by Fourier transforming the complex wave from Fig. 2c with a Fresnel defocus applied. Note the detailed agreement with the experimental figures in a. A similar simulation assuming no azimuthal phase is given in Supplementary Information showing a very different behaviour ruling out the possibility that the black region is caused by shadowing effects from the needle. Intensity profiles are also given in Supplementary Information. c, Through-focus series of the beam half cut by a sharp edge. The rotation of the image throughout the series, indicated by the white arrows, proves the presence of a net negative orbital angular momentum.
We can also prove experimentally that this electron wave now possesses net orbital angular momentum, induced by the interaction with the monopole field, making use of the Gouy phase method27,28, sketched in Supplementary Fig. 1. For waves with net OAM we expect a π rotation of the image when going through focus with a direction of rotation depending on the sign of the OAM. This exact behaviour is observed in Fig. 3c, which shows a clear clockwise rotation when going from under- to over-focus.
These experiments show that our approximation to a Dirac string indeed provides a magnetic monopole field. The difference between a true monopole and this approximation lies in the effects of the flux returning to the needle making the field divergence-free again, as can be seen from the defocused images showing Fresnel fringes from the edge and a reconnection of the phase over the needle (Fig. 3a). This effect is the reason why no forked fringes are observed in the experimental holograms (Supplementary Fig. 3a,b). Detailed holographic simulations showing this subtle reconnection difference between a true monopole and a Dirac string are shown in Supplementary Fig. 7 together with a sketch explaining the creation of the phase singularities in both cases (Supplementary Fig. 8).
The further we go into the far field, the more this effect of the needle disappears and the more the resulting wave becomes a true electron vortex as if the interaction took place with a real monopole. It is expected that a needle presenting an integer charge will allow a vortex with sufficient purity to heal itself, removing this distortion29.
The above experiment shows how quantum experiments with magnetic monopoles are feasible and provides a very promising way to make electron vortices for applications in electron microscopy with an almost eightfold gain in beam intensity while avoiding other unwanted beams as compared with holographic reconstruction methods used at present13,30. The present device is static and its magnetic polarization depends entirely on the shape and material of the needle. However, there are no fundamental obstacles to create a nanoscale solenoid to provide any flux in the Dirac string depending on applied current. This extension would provide a dynamically switchable source of vortex electrons that would be highly desirable to improve the speed, flexibility and signal-to-noise ratio in vortex electron experiments.
Even though an electron microscope was used to conveniently demonstrate the effect, the consequences of this experiment reach much further as the Aharonov–Bohm effect is independent of the speed of the electrons and vortex states can be generated in, for example, solid-state systems where conduction electrons encounter similar monopole fields. Indeed, if a sufficiently coherent electron wave packet in a material would encounter a similar approximate monopole field (for example, generated by a ferromagnetic inclusion), it would gain a topologically protected azimuthal phase, possibly changing its propagation dynamics.
Methods
The needle was prepared from bulk nickel by a FIB instrument using a FEI Helios Nanolab with Ga ions accelerated to 30 kV. After extraction from the bulk sample, a large nickel chunk (∼10 × 3 × 30 μm3) was welded onto an already prepared conical shaped copper base and thinned concentrically. The resulting needle is 21.4 μm long, 700 nm wide at the bottom and 200 nm at the top. The nickel needle and part of its copper base were then extracted and sealed over a gold-plated SiN film. The needle was precisely placed in order for half of its length to hang over a 20 μm circular aperture previously drilled in the Au/SiN film. Electron holography was performed in Lorentz (field free) mode at 300 kV on the Qu-Ant-EM microscope (a double-corrected Titan3 80–300) and is sketched in Supplementary Fig. 1. The Möllensted biprism voltage was set to +180 V to have a large field of view and good sampling of the interference fringes. The phase maps were reconstructed from holograms using the standard Fourier filtering method with a final unwrap step. Such phase maps suffer from the presence of the electrostatic potential, which is corrected by flipping the magnetization of the needle and subtracting the phase maps obtained from two opposite magnetizations. The magnetization state of the needle is changed by tilting the needle 30° and applying a small magnetic field (∼0.15 T) by raising the current in the objective lens to 5% of its full strength. Through-focus series were recorded in the diffraction plane of the Lorentz lens using the highest camera length available (18 m) and recorded on a CCD (charge-coupled device) mounted at the end of a Gatan Quantum Image Filter. The Gouy phase experiment was realized in the exact same conditions, cutting the beam with the sharp edge of an objective aperture to clearly see the rotation effects (Supplementary Fig. 1).
References
Dirac, P. A. M. Quantised singularities in the electromagnetic field. Proc. R. Soc. Lond. A 133, 60–72 (1931).
Milton, K. A., Kalbfleisch, G. R., Luo, W. & Gamberg, L. Theoretical and experimental status of magnetic monopoles. Int. J. Mod. Phys. A 17, 732–747 (2002).
Wu, T. T. & Yang, C. N. Dirac monopole without strings: Monopole harmonics. Nucl. Phys. B 107, 365–380 (1976).
Bonnardeau, M. & Drukier, A. K. Creation of magnetic monopoles in pulsars. Nature Lett. 277, 543–544 (1979).
Frisch, H. J. Quest for magnetic monopoles. Nature 344, 706–707 (1990).
Aad, G. et al. Search for magnetic monopoles in collisions with the ATLAS detector. Phys. Rev. Lett. 109, 261803 (2012).
Castelnovo, C., Moessner, R. & Sondhi, S. L. Magnetic monopoles in spin ice. Nature 451, 42–45 (2008).
Salomaa, M. M. Monopoles in the rotating superfluid helium-3 ab interface. Nature 326, 367–370 (1987).
Cardoso, M., Bicudo, P. & Sacramento, P. D. Confinement of monopole field lines in a superconductor at . Ann. Phys. 323, 337–355 (2008).
Goddard, P. & Olive, D. I. Magnetic monopoles in gauge field theories. Rep. Prog. Phys. 41, 1357–1437 (1978).
Kasama, T., Antypas, Y., Chong, R. K. & Dunin-Borkowski, R. E. Novel approaches for the characterization of electromagnetic fields using electron holography. MRS Proc. 839, 107–118 (2004).
Aharonov, Y. & Bohm, D. Significance of electromagnetic potentials in the quantum theory. Phys. Rev. 115, 485–491 (1959).
Kruit, P. & Lenc, M. Optical properties of the magnetic monopole field applied to electron microscopy and spectroscopy. J. Appl. Phys. 72, 4505–4513 (1992).
Bliokh, K. Y., Bliokh, Y. P., Savel’ev, S. & Nori, F. Semiclassical dynamics of electron wave packet states with phase vortices. Phys. Rev. Lett. 99, 190404 (2007).
Uchida, M. & Tonomura, A. Generation of electron beams carrying orbital angular momentum. Nature 464, 737–739 (2010).
Verbeeck, J., Tian, H. & Schattschneider, P. Production and application of electron vortex beams. Nature 467, 301–304 (2010).
Fukuhara, A., Shinagawa, K., Tonomura, A. & Fujiwara, H. Electron holography and magnetic specimens. Phys. Rev. B 27, 1839–1843 (1983).
Tonomura, A. et al. Observation of Aharonov–Bohm effect by electron holography. Phys. Rev. Lett. 48, 1443–1446 (1982).
Berry, M. V. Optical currents. J. Opt. A 11, 094001 (2009).
Bliokh, K. Y., Bekshaev, A. Y. & Nori, F. Dual electromagnetism: Helicity, spin, momentum and angular momentum. New J. Phys. 15, 033026 (2013).
Cameron, R. P. & Barnett, S. M. Electric-magnetic symmetry and Noether’s theorem. New J. Phys. 14, 123019 (2012).
Lipkin, H. J. & Peshkin, M. Angular momentum paradoxes with solenoids and monopoles. Phys. Lett. B 118, 385–390 (1982).
Chambers, R. G. Shift of an electron interference pattern by enclosed magnetic flux. Phys. Rev. Lett. 5, 3–5 (1960).
Wilczek, F. Magnetic flux, angular momentum, and statistics. Phys. Rev. Lett. 48, 1144–1146 (1982).
Beijersbergen, M., Coerwinkel, R., Kristensen, M. & Woerdman, J. Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 112, 321–327 (1994).
Berry, M. V. Optical vortices evolving from helicoidal integer and fractional phase steps. J. Opt. A 6, 259–268 (2004).
Bliokh, K. Y., Schattschneider, P., Verbeeck, J. & Nori, F. Electron vortex beams in a magnetic field: A new twist on Landau levels and Aharonov–Bohm states. Phys. Rev. X 2, 041011 (2012).
Guzzinati, G., Schattschneider, P., Bliokh, K. Y., Nori, F. & Verbeeck, J. Observation of the Larmor and Gouy rotations with electron vortex beams. Phys. Rev. Lett. 110, 093601 (2013).
Bouchal, Z., Wagner, J. & Chlup, M. Self-reconstruction of a distorted nondiffracting beam. Opt. Commun. 151, 207–211 (1998).
Verbeeck, J. et al. Atomic scale electron vortices for nanoresearch. Appl. Phys. Lett. 99, 203109 (2011).
Acknowledgements
This work was financially supported by the European Research Council under the 7th Framework Program (FP7), ERC grant 246791 COUNTATOMS and ERC Starting Grant 278510 VORTEX. The Qu-Ant-EM microscope was partly funded by the Hercules fund from the Flemish Government. The authors acknowledge financial support from the European Union under the Seventh Framework Program under a contract for an Integrated Infrastructure Initiative, Reference No. 312483-ESTEEM2. R.V.B. acknowledges a PhD fellowship grant from the FWO (Fonds Wetenschappelijk Onderzoek–Vlaanderen).
Author information
Authors and Affiliations
Contributions
A.B. and J.V. conceived the experiment; A.B. designed the sample and carried out the TEM measurements. All authors contributed to theory, data analysis and writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 1969 kb)
Rights and permissions
About this article
Cite this article
Béché, A., Van Boxem, R., Van Tendeloo, G. et al. Magnetic monopole field exposed by electrons. Nature Phys 10, 26–29 (2014). https://doi.org/10.1038/nphys2816
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2816
This article is cited by
-
Tailoring electron beams with high-frequency self-assembled magnetic charged particle micro optics
Nature Communications (2022)
-
3D magnetic imaging using electron vortex beam microscopy
Communications Physics (2022)
-
Control of quantum electrodynamical processes by shaping electron wavepackets
Nature Communications (2021)
-
Controlled creation and annihilation of isolated robust emergent magnetic monopole like charged vertices in square artificial spin ice
Scientific Reports (2021)
-
Universal momentum-to-real-space mapping of topological singularities
Nature Communications (2020)