Abstract
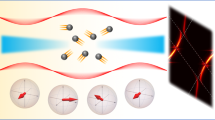
Geometric phases that characterize the topological properties of Bloch bands play a fundamental role in the band theory of solids. Here we report on the measurement of the geometric phase acquired by cold atoms moving in one-dimensional optical lattices. Using a combination of Bloch oscillations and Ramsey interferometry, we extract the Zak phase—the Berry phase gained during the adiabatic motion of a particle across the Brillouin zone—which can be viewed as an invariant characterizing the topological properties of the band. For a dimerized lattice, which models polyacetylene, we measure a difference of the Zak phase δ φZak = 0.97(2)π for the two possible polyacetylene phases with different dimerization. The two dimerized phases therefore belong to different topological classes, such that for a filled band, domain walls have fractional quantum numbers. Our work establishes a new general approach for probing the topological structure of Bloch bands inoptical lattices.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Jackiw, R. & Rebbi, C. Solitons with fermion number 1/2. Phys. Rev. D 13, 3398–3409 (1976).
Goldstone, J. & Wilczek, F. Fractional quantum numbers on solitons. Phys. Rev. Lett. 47, 986–989 (1981).
Su, W. P., Schrieffer, J. R. & Heeger, A. J. Solitons in polyacetylene. Phys. Rev. Lett. 42, 1698–1701 (1979).
Bell, J. S. & Rajaraman, R. On states, on a lattice, with half-integer charge. Nucl. Phys. B 220, 1–12 (1983).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).
Xiao, D., Chang, M-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X. & Zhang, S. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 392, 45–57 (1984).
Kitaev, A. Periodic table for topological insulators and superconductors. AIP Conf. Proc. 1134, 22–30 (2009).
Ryu, S., Schneider, A., Furusaki, A. & Ludwig, A. Topological insulators and superconductors: tenfold way and dimensional hierarchy. New J. Phys. 12, 065010 (2010).
Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 62, 2747–2750 (1989).
Ryu, S. & Hatsugai, Y. Topological origin of zero-energy edge states in particle–hole symmetric systems. Phys. Rev. Lett. 89, 077002 (2002).
Delplace, P., Ullmo, D. & Montambaux, G. Zak phase and the existence of edge states in graphene. Phys. Rev. B 84, 195452 (2011).
Niemi, A. J. & Semenoff, G. W. Spectral asymmetry on an open space. Phys. Rev. D 30, 809–818 (1984).
Rice, M. J. & Mele, E. J. Elementary excitations of a linearly conjugated diatomic polymer. Phys. Rev. Lett. 49, 1455–1459 (1982).
Alba, E. et al. Seeing topological order in time-of-flight measurements. Phys. Rev. Lett. 107, 235301 (2011).
Zhao, E. et al. Chern numbers hiding in time-of-flight images. Phys. Rev. A 84, 063629 (2011).
Goldman, N. et al. Measuring topology in a laser-coupled honeycomb lattice: From Chern insulators to topological semi-metals. New J. Phys. 15, 013025 (2013).
Price, H. M. & Cooper, N. R. Mapping the Berry curvature from semiclassical dynamics in optical lattices. Phys. Rev. A 85, 033620 (2012).
Fölling, S. et al. Direct observation of second-order atom tunnelling. Nature 448, 1029–1032 (2007).
Wannier, G. H. Dynamics of band electrons in electric and magnetic fields. Rev. Mod. Phys. 34, 645–655 (1962).
King-Smith, R. D. & Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651–1654 (1993).
Ben Dahan, M., Peik, E., Reichel, J., Castin, Y. & Salomon, C. Bloch oscillations of atoms in an optical potential. Phys. Rev. Lett. 76, 4508–4511 (1996).
Weitenberg, C. et al. Single-spin addressing in an atomic Mott insulator. Nature 471, 319–324 (2011).
Kitagawa, T. et al. Observation of topologically protected bound states in photonic quantum walks. Nature Commun. 3, 882 (2012).
Kraus, Y. E. et al. Topological states and adiabatic pumping in quasicrystals. Phys. Rev. Lett. 109, 106402 (2012).
Ruostekoski, J., Dunne, G. & Javanainen, J. Particle number fractionalization of an atomic Fermi–Dirac gas in an optical lattice. Phys. Rev. Lett. 88, 180401 (2002).
Grusdt, F., Hoening, M. & Fleischhauer, M. Topological edge states in the one-dimensional super-lattice Bose–Hubbard model. Phys. Rev. Lett. 110, 260405 (2013).
Abanin, D. et al. Interferometric approach to measuring band topology in 2D optical lattices. Phys. Rev. Lett. 110, 165304 (2013).
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Grifoni, M. & Hänggi, P. Driven quantum tunneling. Phys. Rep. 304, 229–354 (1998).
Kitagawa, T., Berg, E., Rudner, M. & Demler, E. Topological characterization of periodically driven quantum systems. Phys. Rev. B 82, 235114 (2010).
Lindner, N. H., Refael, G. & Galitski, V. Floquet topological insulator in semiconductor quantum wells. Nature Phys. 7, 490–495 (2011).
Volovik, G. E. The Universe in a Helium Droplet (Oxford Univ. Press, 2003).
Acknowledgements
We acknowledge helpful discussions with B. Paredes. We thank Y-A. Chen and S. Nascimbène for their help in setting up the experiment and for their comments in the early stages of the experiment. This work was supported by the DFG (FOR635, FOR801), NIM, DARPA (OLE program), Harvard-MIT CUA, the ARO-MURI on Atomtronics, and the ARO MURI Quism program. M. Aidelsburger was further supported by the Deutsche Telekom Stiftung.
Author information
Authors and Affiliations
Contributions
M. Atala, M. Aidelsburger and J.T.B. carried out the experiments and the data analysis. D.A., T.K. and E.D. carried out the theoretical analysis and derived the measurement protocol. I.B. and E.D. supervised the work and developed the general measurement idea. All authors contributed extensively to the analysis and the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 960 kb)
Rights and permissions
About this article
Cite this article
Atala, M., Aidelsburger, M., Barreiro, J. et al. Direct measurement of the Zak phase in topological Bloch bands. Nature Phys 9, 795–800 (2013). https://doi.org/10.1038/nphys2790
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2790
This article is cited by
-
Reconfigurable quantum fluid molecules of bound states in the continuum
Nature Physics (2024)
-
Quantum time reflection and refraction of ultracold atoms
Nature Photonics (2024)
-
Emerging topological bound states in Haldane model zigzag nanoribbons
npj Quantum Materials (2024)
-
Topological phenomena in honeycomb Floquet metamaterials
Mathematische Annalen (2024)
-
Bloch oscillations of coherently driven dissipative solitons in a synthetic dimension
Nature Physics (2023)