Abstract
Newton’s third law of motion is one of the pillars of classical physics. This fundamental principle states that the forces two bodies exert on each other are equal and opposite. Had the resulting accelerations been oriented in the same direction, this would have instead led to a counterintuitive phenomenon, that of diametric drive1. In such a hypothetical arrangement, two interacting particles constantly accelerate each other in the same direction through a violation of the action–reaction symmetry. Although in classical mechanics any realization of this process requires one of the two particles to have a negative mass and hence is strictly forbidden, it could nevertheless be feasible in periodic structures where the effective mass can also attain a negative sign2,3,4,5,6,7. Here we report the first experimental observation of such diametric drive acceleration for pulses propagating in a nonlinear optical mesh lattice8,9,10,11,12,13,14. The demonstrated reversal of action–reaction symmetry could enable altogether new possibilities for frequency conversion and pulse-steering applications.
Similar content being viewed by others
Main
Newton’s third law states that action–reaction forces involved in an elemental two-body interaction must be equal and opposite: F1 = −F2. Combined with the second law of motion, this leads to m1a1 = −m2a2, where m1,2 represent the masses of these two particles and a1,2 their respective accelerations. Given that mass is by nature a positive quantity, two classical bodies are expected to accelerate either towards or away from each other, but never in the same direction (Fig. 1a). However, this situation completely changes if hypothetically one of the masses is negative. In fact, in this regime, an intriguing scenario arises whenever m1 = −m2; under these conditions, two interacting bodies will indefinitely accelerate in the same direction while keeping a constant distance among themselves (Fig. 1a). Interestingly, this possibility was first speculated within the context of diametric drive that could itself provide a possible mechanism for space propulsion1. Of course, given that in classical mechanics the mass of a particle is always positive, no such acceleration behaviour that breaks the action–reaction symmetry has ever been reported.
a, Two bodies of positive masses accelerate towards each other in the presence of attractive forces. In contrast, two particles with equal and opposite in sign masses tend to self-accelerate when subject to the same force (schematic illustration). b, Set-up of two time-multiplexed fibre loops with length difference ΔL, connected through a 50/50 coupler. Sequences of light pulses circulating in both loops obey the same dynamics as in a spatial mesh lattice8,10. The nonlinearity in the fibres introduces a nonlinear phase shift on each pulse that is proportional to its peak power. c, Dispersion diagram associated with two oppositely curved bands. The upper (lower) band has a positive (negative) curvature and therefore exhibits a positive (negative) effective photon mass that is inverse to the curvature. The Kerr nonlinearity tends to focus excitations in the upper band whereas the corresponding effects in the lower band are of the defocusing type. Q, wave number; θ, propagation constant. See Supplementary Methods for details.
Waves on the other hand are free of such limitations. In the case of a free quantum particle governed by the Schrödinger equation, the resulting parabolic dispersion relation between energy and momentum has a positive curvature defined by the particle’s mass. Meanwhile, quasiparticles such as electrons and holes in solid-state crystals, mass–spring systems5 or collective excitations such as Bose–Einstein condensates in lattices6,7 may exhibit a dispersion relation with regions of inverted curvature where the effective mass is negative. Similarly, in photonic guiding structures, the effective photon mass can be positive or negative depending on the sign of the associated group velocity dispersion3,4. In addition, photonic lattices such as waveguide arrays15,16 or mesh lattices8,9,10,11,12 provide a versatile environment to experimentally investigate this class of phenomena, as broad light excitations of these structures are effectively governed by their respective mass that can be either positive or negative (Fig. 1c). The second component needed for realizing a diametric drive is an effective interaction between the two entities involved. Although in general such forces can emerge from a number of physical processes, in optics, this can be achieved only through nonlinear effects. For example in waveguide structures, optical wave packets can interact through third-order Kerr nonlinearity—in direct analogy to point-like scattering in Bose–Einstein condensates6,7,17. In this setting, an effective force is established between two partially overlapping light beams2,18,19. Therefore, nonlinear optical periodic configurations can serve as an ideal platform to observe diametric drive acceleration and to study action–reaction symmetry breaking effects.
Here we experimentally demonstrate such optical self-accelerating bound states in a temporal mesh lattice. A composite beam or a wave packet is formed by a sequence of circulating optical pulses11,12 propagating in two fibre loops connected by a 50/50 coupler10 (Fig. 1b and Supplementary Methods). A length difference ΔL between the two loops essentially creates an effective grid of positions or time slots n that are coupled to their nearest neighbours at every propagation step or loop round-trip s. A light pulse propagating in the short loop takes a shortcut and thus advances by a fixed time amount, moving its time slot to the left from n+1 to n. In contrast, a pulse circulating in the long loop is delayed from n−1 to n. After each round trip s, pulse sequences in both loops are linearly interfered by the matrix

of the central 50/50 coupler. In the linear optical regime of low pulse powers, this results in the following system of coupled evolution equations10:

Here, uns and vns are the pulse amplitudes at the time slot or position n and propagation step s circulating in the short and long loop, respectively. The term φ(n) denotes the external phase shift being imprinted onto the field during each round trip by a phase modulator in the short loop. Similar to cases where a refractive index distribution is present, this phase accumulates during evolution and affects the interference between neighbouring pulses. Hence, φ(n) can be regarded as a position-dependent effective potential.
The required interaction between optical pulses is provided by the Kerr nonlinearity of the optical fibres themselves. The pulse powers needed to induce these nonlinear effects are sustained by employing erbium-doped fibre amplifiers that compensate for round-trip losses.
In our set-up, the resulting nonlinear pulse dynamics are described by14:


where the coefficient χ represents the accumulated nonlinearity in each loop (Supplementary Methods).
As previously indicated, the arrangement used here is in every respect equivalent to a periodic mesh lattice and as such it exhibits a band structure8,10. The corresponding dispersion relation is obtained by using discrete Floquet–Bloch modes (uns,vns)∼e−iθs/2eiQn/2, in the linear equation (1) (Supplementary Methods). The resulting band structure relates the propagation eigenvalue θ to the Bloch momentum Q by cosθ = (1/2)(cosQ−1). Our system exhibits two symmetric bands with opposite curvatures or group-velocity dispersion—in contact at a zero-dispersion point located at the edge of the Brillouin zone (Fig. 1c). Photons excited in the lower band have a negative effective mass, whereas for those in the upper branch this same quantity is positive.
In our experiments, we use two broad pulse sequences having a Gaussian envelope (Fig. 2a). The phase relation between the two loops is appropriately set by external phase modulation so that the left Gaussian wave packet or beam populates the upper band, whereas the right one occupies the lower branch (Supplementary Methods).
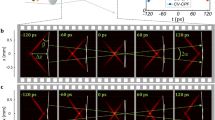
a, In the case of a flat potential (φ(n) = 0), the left beam with a positive mass and the right beam (with negative mass) behave in a very similar fashion. The slight asymmetry is caused by a minor degree of nonlinearity present in the experiment. b, The positive-mass beam is pulled towards the valley, where the negative-mass beam is reflected. c, The left beam with meff>0 is repelled by a hill, whereas the right beam with meff<0 is now attracted. d, When a potential valley precedes a hill, both beams are reflected, but at different positions. See Supplementary Fig. S7 for details and a comparison of these results with the trajectory of a classical particle.
To demonstrate the analogy between our results and mechanical objects with positive and negative mass, we first perform a linear scattering experiment (χ≈0) on a smooth potential hill or valley, as imposed by the external phase modulation φ(n) (Fig. 2). In the absence of any external potential (φ(n) = 0), the two wave packets propagate at a constant velocity (at a constant slope) very much like free quantum mechanical particles while at the same time experiencing broadening because of dispersion (Fig. 2a). This situation changes in the presence of a potential. From a mechanical perspective, an object with a positive mass will be eventually attracted and hence accelerated towards a valley with decreasing potential (φ(n) decreasing). On the other hand, had the mass of this particle been negative, it would have instead been repelled by this same potential valley (Fig. 2b). The converse is true when experiencing the effects of a potential hill where the phase φ(n) increases. In this scenario, the positive mass entity is repelled whereas that with negative mass is attracted (Fig. 2c). Optical experiments confirming this behaviour in linear mesh lattices are shown in Fig. 2b,c. In this arrangement, the optical wave packets undergo different accelerations depending on the sign of the curvature of the band they originate from. Figure 2d also depicts what happens when a potential valley precedes a hill. In such a configuration a positive-mass wave is first attracted and then repelled, in contradistinction with the case of a negative-mass beam. It is worth noting that the acceleration effects presented in Fig. 2b,c are an outcome of wave dynamics under the action of an external potential. Unlike self-bending Airy beams20,21,22,23,24,25,26 that always accelerate in a unique fashion, here the attraction/repulsion dynamics are dictated by the sign of the effective mass governed by the band curvature.
The dynamics of these two beams become even more intriguing when they start interacting without an external potential (φ(n) = 0) through the nonlinear response of the fibre (χ>0). In this regime, a Gaussian excitation in the upper band experiences self-focusing that in conjunction with dispersive effects leads to a stable localized state. The measurement in Fig. 3a represents an experimental demonstration of this new class of solitary waves—discrete-time solitons in mesh lattices. In contrast, when the same Gaussian excitation excites the lower band (where the effective mass is negative), the nonlinearity reverses its action and induces strong nonlinear defocusing effects (Fig. 3b).
a, When the upper band is excited, nonlinear self-phase modulation counteracts dispersive spreading. As a result, a stable discrete soliton is formed. b, On the other hand, by exciting the lower band with a Gaussian pulse sequence, nonlinear defocusing occurs. See Supplementary Figs S8 and S9.
In our set-up, optical diametric drive acceleration is realized by allowing the self-trapped wave packet of Fig. 3a to nonlinearly interact with the defocusing beam shown in Fig. 3b. While the positive-mass soliton is attracted by the negative-mass beam, the latter is constantly repelled. As a result, the positive-mass beam will permanently pursue its negative-mass counterpart while the latter one tries to escape. In this respect, a self-propelled bound state forms, provided that both beams exhibit identical accelerations. According to Newton’s third law, this requires that the masses of these two constituents are equal but opposite in sign. Given that the effective photon masses in both bands of a mesh lattice have the same absolute value, the negative-mass beam should carry roughly the same number of photons as its positive-mass counterpart to achieve diametric drive acceleration.
To excite such a self-accelerating bound state, we launch two optical Gaussian wave packets having opposite masses, in close proximity to each other (Fig. 4a). A slight frequency detuning between the two beams ensures that their interaction is incoherent and restricted to pure cross-phase modulation. Still all fields within the same band remain fully coherent with respect to each other (Supplementary Methods). Our experimental results (Fig. 4) show the formation of such a mass/anti-mass self-accelerating state. In all cases, this combined entity accelerates towards the direction of the negative-mass component. Even though the particle perspective provides an insightful picture in terms of understanding the working principles behind diametric drive, it cannot fully account for the wave-like nature of the beams involved in our experiment. In particular, all interacting waves remain surprisingly well localized even after an appreciable propagation distance. This could be expected for the positive-mass soliton component (because of self-trapping) but is totally counterintuitive for the negative-mass beam that is meant to undergo spreading as a result of nonlinearity (Fig. 3b). What explains this odd behaviour is the fact that any spreading in the direction of propagation becomes eventually suppressed because of acceleration; the repelling action of the solitonic part tends to block the negative-mass beam from spreading further into the interaction region.
A bound state involving a soliton in the focusing positive-mass band and a wave packet from the lower band (meff<0) self-accelerates by reversing the action–reaction symmetry. a,b, Nonlinear pulse dynamics in the short loop (a) and numerical evaluation of equation (2) when χ = 1.2 (b). The bound state accelerates until reaching the limiting velocity vmax. The hyperbolic trajectory of a relativistic particle subject to constant acceleration assuming c = vmax is overlaid (white dashed lines) to demonstrate the conceptual analogy. c,d, Measured and simulated total intensity profiles after m = 150 steps.
Note that in the double-loop configuration employed, all group velocities are limited to a maximum value of  positions per roundtrip, a restriction arising from the maximum inclination of the band structure8. During acceleration, the bound state inevitably shifts its Fourier spectrum away from the centre towards the edges of the Brillouin zone. Hence, during this process, the local curvature of the band structure is continuously reduced, leading to an increase in the effective mass of the interacting pulses. Although the diametric drive mechanism is still at play, the attained acceleration slows down. This is directly analogous to a relativistic particle whose mass seems to increase during the course of acceleration and therefore cannot exceed the velocity of light. The hyperbolic trajectory of a constantly accelerated relativistic particle viewed from an inertial reference frame27 coincides well with the motion of our optical diametric drive (dashed white line overlaid to Fig. 4a,b; see Supplementary Methods), thus proving the ongoing action of the propulsion mechanism.
positions per roundtrip, a restriction arising from the maximum inclination of the band structure8. During acceleration, the bound state inevitably shifts its Fourier spectrum away from the centre towards the edges of the Brillouin zone. Hence, during this process, the local curvature of the band structure is continuously reduced, leading to an increase in the effective mass of the interacting pulses. Although the diametric drive mechanism is still at play, the attained acceleration slows down. This is directly analogous to a relativistic particle whose mass seems to increase during the course of acceleration and therefore cannot exceed the velocity of light. The hyperbolic trajectory of a constantly accelerated relativistic particle viewed from an inertial reference frame27 coincides well with the motion of our optical diametric drive (dashed white line overlaid to Fig. 4a,b; see Supplementary Methods), thus proving the ongoing action of the propulsion mechanism.
In conclusion, we have experimentally demonstrated diametric drive acceleration in time-domain optical mesh lattices. This was accomplished by involving two wave packets with equal but opposite in sign effective masses. The underlying concept presented here is quite general and can directly apply to many other physical settings. Given that the effective mass is a generic concept in physics, diametric drive effects can inspire new approaches in controlling particle interactions in crystal lattices. The demonstrated reversal of action–reaction symmetry in optics could also enable new possibilities for frequency conversion and pulse steering applications, as in figure-eight laser systems or during supercontinuum generation in photonic crystal fibres18,19,26,28,29,30.
References
Millis, M. G. Challenge to create the space drive. J. Prop. Power 13, 577–582 (1997).
Batz, S. & Peschel, U. Diametrically driven self-accelerating pulses in a photonic crystal fiber. Phys. Rev. Lett. 110, 193901 (2013).
Luo, C., Johnson, S., Joannopoulos, J. & Pendry, J. All-angle negative refraction without negative effective index. Phys. Rev. B 65, 201104 (2002).
Notomi, M. Theory of light propagation in strongly modulated photonic crystals: Refractionlike behavior in the vicinity of the photonic band gap. Phys. Rev. B 62, 10696–10705 (2000).
Yao, S., Zhou, X. & Hu, G. Experimental study on negative effective mass in a 1D mass–spring system. New J. Phys. 10, 43020 (2008).
Morsch, O. & Oberthaler, M. Dynamics of Bose–Einstein condensates in optical lattices. Rev. Mod. Phys. 78, 179–215 (2006).
Sakaguchi, H. & Malomed, B. A. Dynamics of positive- and negative-mass solitons in optical lattices and inverted traps. J. Phys. B. 37, 1443–1459 (2004).
Miri, M-A., Regensburger, A., Peschel, U. & Christodoulides, D. Optical mesh lattices with PT symmetry. Phys. Rev. A 86, 023807 (2012).
Bouwmeester, D., Marzoli, I., Karman, G., Schleich, W. & Woerdman, J. Optical Galton board. Phys. Rev. A 61, 013410 (1999).
Regensburger, A. et al. Parity–time synthetic photonic lattices. Nature 488, 167–171 (2012).
Schreiber, A. et al. Photons walking the line: A quantum walk with adjustable coin operations. Phys. Rev. Lett. 104, 050502 (2010).
Schreiber, A. et al. A 2D quantum walk simulation of two-particle dynamics. Science 336, 55–58 (2012).
Dreisow, F. et al. Spatial light rectification in an optical waveguide lattice. Europhys. Lett. 101, 44002 (2013).
Navarrete-Benlloch, C., Pérez, A. & Roldán, E. Nonlinear optical Galton board. Phys. Rev. A 75, 062333 (2007).
Lederer, F. et al. Discrete solitons in optics. Phys. Rep. 463, 1–126 (2008).
Eisenberg, H., Silberberg, Y., Morandotti, R. & Aitchison, J. Diffraction management. Phys. Rev. Lett. 85, 1863–1866 (2000).
Denschlag, J. Generating solitons by phase engineering of a Bose–Einstein condensate. Science 287, 97–101 (2000).
Demircan, A. et al. Rogue events in the group velocity horizon. Sci. Rep. 2, 850 (2012).
Demircan, A., Amiranashvili, S. & Steinmeyer, G. Controlling light by light with an optical event horizon. Phys. Rev. Lett. 106, 163901 (2011).
Siviloglou, G., Broky, J., Dogariu, A. & Christodoulides, D. Observation of accelerating Airy beams. Phys. Rev. Lett. 99, 213901 (2007).
Ellenbogen, T., Voloch-Bloch, N., Ganany-Padowicz, A. & Arie, A. Nonlinear generation and manipulation of Airy beams. Nature Photon. 3, 395–398 (2009).
Minovich, A. et al. Generation and near-field imaging of Airy surface plasmons. Phys. Rev. Lett. 107, 116802 (2011).
Kaminer, I., Bekenstein, R., Nemirovsky, J. & Segev, M. Nondiffracting accelerating wave packets of Maxwell’s equations. Phys. Rev. Lett. 108, 163901 (2012).
Hu, Y. et al. Reshaping the trajectory and spectrum of nonlinear Airy beams. Opt. Lett. 37, 3201–3203 (2012).
Voloch-Bloch, N., Lereah, Y., Lilach, Y., Gover, A. & Arie, A. Generation of electron Airy beams. Nature 494, 331–335 (2013).
Ament, C., Polynkin, P. & Moloney, J. V. Supercontinuum generation with femtosecond self-healing Airy pulses. Phys. Rev. Lett. 107, 243901 (2011).
Born, M. Die Theorie des starren Elektrons in der Kinematik des Relativitätsprinzips. Ann. Phys. 335, 1–56 (1909).
Driben, R. & Babushkin, I. Accelerated rogue waves generated by soliton fusion at the advanced stage of supercontinuum formation in photonic-crystal fibers. Opt. Lett. 37, 5157–5159 (2012).
Gorbach, A. V. & Skryabin, D. V. Light trapping in gravity-like potentials and expansion of supercontinuum spectra in photonic-crystal fibres. Nature Photon. 1, 653–657 (2007).
Philbin, T. G. et al. Fiber-optical analog of the event horizon. Science 319, 1367–1370 (2008).
Acknowledgements
We would like to thank G. Leuchs for providing equipment and B. Malomed for fruitful discussions. Moreover, we acknowledge financial support from DFG Forschergruppe 760, DFG Project PE 523/10-1, German Max Planck Society for the Advancement of Science (MPG), Cluster of Excellence Engineering of Advanced Materials (EAM) and School of Advanced Optical Technologies (SAOT). This work was also supported by NSF ECCS-1128520 and by AFOSR grant FA95501210148.
Author information
Authors and Affiliations
Contributions
M.W. performed the measurements. M.W., A.R., C.B. and G.O. built and designed the experiment. M-A.M., S.B., D.N.C. and U.P. developed the theoretical background. S.B. and U.P. conceived the concept of diametric drive in optics.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 1283 kb)
Rights and permissions
About this article
Cite this article
Wimmer, M., Regensburger, A., Bersch, C. et al. Optical diametric drive acceleration through action–reaction symmetry breaking. Nature Phys 9, 780–784 (2013). https://doi.org/10.1038/nphys2777
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2777
This article is cited by
-
High-order dynamic localization and tunable temporal cloaking in ac-electric-field driven synthetic lattices
Nature Communications (2022)
-
All-optical supercontinuum switching
Communications Physics (2020)
-
Observation of localized modes at effective gauge field interface in synthetic mesh lattice
Scientific Reports (2019)
-
Anderson localization of a one-dimensional quantum walker
Scientific Reports (2018)
-
Anderson localization in synthetic photonic lattices
Scientific Reports (2017)