Abstract
Quantum theory is often presented as the theory describing the microscopic world, and admittedly, it has done this extremely well for decades. Nonetheless, the question of whether it applies to macroscopic scales remains open, despite many efforts1,2,3. Here, we report on entanglement exhibiting strong analogies with the Schrödinger cat state as it involves two macroscopically distinct states- two states that can be efficiently distinguished using detectors with no microscopic resolution4. Specifically, we start by generating entanglement between two spatial optical modes at the single-photon level and subsequently displace one of these modes up to almost a thousand photons5. To reliably check whether entanglement is preserved, the state is redisplaced back to the single-photon level and a well-established entanglement measure6, based on single-photon detection, is applied. Our results provide a tool to address fundamental questions about quantum theory and hold potential for more applied problems, for instance in quantum sensing.
Similar content being viewed by others
Main
Can quantum features, such as entanglement, survive in the macro domain? This natural question has been with us since the inception of quantum theory. Nowadays, decoherence is widely accepted as one of the fundamental problems limiting the ability of macro systems to maintain quantum features7. As the size of a quantum system increases, it more and more intensively interacts with its surroundings, rapidly destroying its quantum properties. A few technologically demanding experiments1,2,3 have beautifully strengthened this idea. We also know that even if a system is sufficiently well de-coupled from the environment to hold its quantum features, they remain difficult to observe. One of the problems is that decoherence mechanisms inevitably increase the Hilbert space dimension, and even if a small amount of quantumness can survive, the system is no longer well described by the relatively simple theoretical models where measures are known for certifying quantum behaviour. This led, for example, to lively debates8,9,10,11,12 about the presence of entanglement in the experiment reported in ref. 13 where one photon from an entangled pair was phase-covariantly cloned. Measurement precision is another issue. Even if a macro system could be perfectly isolated from its environment, its quantum nature would require extremely precise measurements to be observed14,15.
Following the theoretical proposal presented in ref. 5, we here report on the first experiment where entanglement is created in the micro domain and subsequently displaced to the macro domain, following the spirit of the Schrödinger cat experiment. The displacement is accurately controlled and allows for extending entanglement over unexplored regimes, ranging continuously from a single photon to almost a thousand. Under displacement, the entangled state becomes macroscopic not only because of the large mean photon number but also because its components could be distinguished in a single shot with classical detectors, that is, photon counting detectors coarse-grained by thermal noise, allowing one to resolve only large photon number differences. To check whether entanglement survives in the macro domain, the state is locally displaced back to the micro domain before being detected. This alleviates the problems of detecting macroscopic entanglement because on the one hand, the existence of entanglement can be proved with a well-established entanglement measure operating in the micro domain and on the other hand, the problem of the measurement precision is relegated to the displacement, which can be performed very accurately.
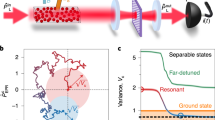
The experiment starts with the heralded creation of a path-entangled state lying in the micro domain (see Fig. 1). A nonlinear optical crystal is pumped by a pulsed laser in the picosecond regime to produce telecom photon pairs by means of spontaneous parametric down-conversion. We set the pump intensity such that the probability of creating a single pair per run is very small. Thus, the detection of one idler photon heralds the creation of a single signal photon. By further placing a narrowband filter before the heralding detector, the signal photons are heralded in spectrally pure states with a bandwidth limited by the pump spectrum. To ensure their spatial purity, they are coupled into a monomode fibre with an efficiency of 50%. The measurement of the second-order auto-correlation g(2)(0) = 1.9(1) unambiguously demonstrates the purity of the signal field16. By sending the heralded photon into a balanced beam splitter, one obtains, leaving aside the loss, a maximally entangled state that describes the two output modes A and B sharing a single photon  This path-entangled state, known as single-photon entanglement, can be seen as the signature of the non-classical feature of the heralded signal photon17,18.
This path-entangled state, known as single-photon entanglement, can be seen as the signature of the non-classical feature of the heralded signal photon17,18.
Sources, A Ti:sapphire laser pulsed in the picosecond regime with a 76 MHz repetition rate at 780 nm pumps two periodically poled lithium niobate (PPLN) bulk crystals. In one crystal, pairs of photons are generated by type II spontaneous parametric down-conversion and separated by a polarizing beam splitter (PBS). One photon is sent through a 25 GHz filter (f) at a central wavelength of 1,563 nm, and detected in a gated avalanche photodiode (APD) with 20% detection efficiency. The second PPLN crystal is seeded by an additional continuous-wave (c.w.) laser at 1,563 nm, generating a local oscillator (by means of pulsed coherent state) through DFG, whose bandwidth is restricted by energy conservation to the bandwidth of the pump laser. Micro entanglement, the heralded single photon (HSP) is sent to a fibre 50/50 beam splitter, realizing an entangled state between the two output modes A and B. The figure-8 shapes represents the entanglement between the two modes. Macro entanglement, the mode A is then combined with the local oscillator on a unbalanced beam splitter (90/10), corresponding to a displacement operation on the HSP state. A set of black lines represents the fact that in this mode the state can be seen as macroscopic. Analysis, the measurement set-up consists of the application, on the mode A, of an inverse displacement operation  by means of another 90/10 fibre beam splitter that closes a Mach–Zehnder interferometer. The adjustable U-bench allows one to accurately balance the path length difference for the experimental wavelength and to stabilize the phase on the side of the interference fringe from a reference laser (see Supplementary Information). In this interferometer, a piezo (PZT) is used to compensate the phase fluctuations. The PZT on the mode B is used to observe single-photon interference fringes. A pair of PBSs and a half-waveplate (HWP) are used to recombine the modes A and B (HWP at π/8) or not (HWP at 0) to access V or pi j, respectively (see the main text). The two outputs are detected by two avalanche photodiodes with 25% detection efficiency, triggered by the detection of an idler photon in the HSPs.
by means of another 90/10 fibre beam splitter that closes a Mach–Zehnder interferometer. The adjustable U-bench allows one to accurately balance the path length difference for the experimental wavelength and to stabilize the phase on the side of the interference fringe from a reference laser (see Supplementary Information). In this interferometer, a piezo (PZT) is used to compensate the phase fluctuations. The PZT on the mode B is used to observe single-photon interference fringes. A pair of PBSs and a half-waveplate (HWP) are used to recombine the modes A and B (HWP at π/8) or not (HWP at 0) to access V or pi j, respectively (see the main text). The two outputs are detected by two avalanche photodiodes with 25% detection efficiency, triggered by the detection of an idler photon in the HSPs.
The second step consists of amplifying the mode A by applying a unitary operation  corresponding to a displacement in the phase space. The displacement is obtained by combining the mode A and an intense local oscillator on a highly unbalanced beam splitter19,20. The physics behind the displacement is based on an interference process. Hence, the field A and the local oscillator need to be indistinguishable. This is ensured in practice by producing the local oscillator by means of a difference frequency generation (DFG), using an identical nonlinear crystal to the one used for the photon pair creation but stimulated by a continuous-wave telecom laser. The indistinguishability between the resulting local oscillator and the field A is confirmed through a Hong–Ou–Mandel (HOM) type interference21 whose dip, reported in Fig. 2, has a visibility limited only by the reflectivity of the beam splitter and the photon statistics. As such, after the displacement, the detection of an idler photon heralds the generation of an entangled state of the form
corresponding to a displacement in the phase space. The displacement is obtained by combining the mode A and an intense local oscillator on a highly unbalanced beam splitter19,20. The physics behind the displacement is based on an interference process. Hence, the field A and the local oscillator need to be indistinguishable. This is ensured in practice by producing the local oscillator by means of a difference frequency generation (DFG), using an identical nonlinear crystal to the one used for the photon pair creation but stimulated by a continuous-wave telecom laser. The indistinguishability between the resulting local oscillator and the field A is confirmed through a Hong–Ou–Mandel (HOM) type interference21 whose dip, reported in Fig. 2, has a visibility limited only by the reflectivity of the beam splitter and the photon statistics. As such, after the displacement, the detection of an idler photon heralds the generation of an entangled state of the form

|α〉A results from the displacement of the vacuum, which follows a Poissonian photon number distribution with mean photon number |α|2 equal to the variance.  represents the displacement of a single photon that is a non-Gaussian state characterized by a photon number distribution with a mean photon number |α|2+1 and a variance 3|α|2. Although |α〉A and
represents the displacement of a single photon that is a non-Gaussian state characterized by a photon number distribution with a mean photon number |α|2+1 and a variance 3|α|2. Although |α〉A and  differ by only one photon on average, the distance between their photon number distributions is about the square root of their size. Checking whether the photon number falls in the interval [|α|2−|α|,|α|2+|α|] or not, allows one to distinguish their photon number distributions with a probability that increases with the size and approaches 74% in the limit of large |α|. This probability goes up to 90% if the state (1) is seen in another basis so that it reads
differ by only one photon on average, the distance between their photon number distributions is about the square root of their size. Checking whether the photon number falls in the interval [|α|2−|α|,|α|2+|α|] or not, allows one to distinguish their photon number distributions with a probability that increases with the size and approaches 74% in the limit of large |α|. This probability goes up to 90% if the state (1) is seen in another basis so that it reads  by dividing the photon number into two intervals [0,|α|2] and
by dividing the photon number into two intervals [0,|α|2] and  (for real positive α). This allows one to distinguish efficiently the two components of the displaced mode with classical detectors, which we now describe. Any measurement of the photon number can be pictured as a pointer on a scale that is shifted when photons are detected (the larger the photon number is, the further the pointer shifts). If the initial state of the pointer is not a delta-function, but has a large spread, for example, due to thermal noise, the probability to distinguish a single photon from the vacuum state in a single shot approaches that of a simple guess. We call such a measurement classical, because it does not resolve the quantum features in the micro domain. On the contrary, the probability to distinguish the states
(for real positive α). This allows one to distinguish efficiently the two components of the displaced mode with classical detectors, which we now describe. Any measurement of the photon number can be pictured as a pointer on a scale that is shifted when photons are detected (the larger the photon number is, the further the pointer shifts). If the initial state of the pointer is not a delta-function, but has a large spread, for example, due to thermal noise, the probability to distinguish a single photon from the vacuum state in a single shot approaches that of a simple guess. We call such a measurement classical, because it does not resolve the quantum features in the micro domain. On the contrary, the probability to distinguish the states  and
and  in a single shot with such a classical measurement approaches 90% (for large enough α). This makes the state (1) analogous to the famous Schrödinger’s cat state where the dead and alive components can be distinguished without microscopic resolution4.
in a single shot with such a classical measurement approaches 90% (for large enough α). This makes the state (1) analogous to the famous Schrödinger’s cat state where the dead and alive components can be distinguished without microscopic resolution4.
a, HOM type interference between the heralded single photon in mode A and the local oscillator that is used to displace it. This is obtained by varying the arrival time of the local oscillator onto the first 90:10 beam splitter (Fig. 1) and recording the twofold coincidences at the outputs of the beam splitter. The experimental results (red dots) exhibit a dip with a visibility of 23(4)%. b, The lower bound on the concurrence as a function of the mean photon number |α|2. The concurrence decreases when the photon number increases, as expected, but remains positive up to nearly 550 photons. The value of the underlying parameters (V, p00, p01, p10, and p11) can be found in the Supplementary Information. They are all based on raw counts, without subtracting dark counts and accidental coincidences. The full line is obtained from a theoretical model that uses independent measurements (see the main text). The inset shows the photon number probability distribution for |α〉 (red) and  (blue). (For both, the error bars are the standard deviation of 100 acquisitions per point.)
(blue). (For both, the error bars are the standard deviation of 100 acquisitions per point.)
In the last step of the experiment where we wish to probe whether entanglement survives as its size increases, the displaced state in mode A undergoes another displacement  which ideally returns it back to the single-photon level. In practice, the de-amplification is realized in a similar manner as the amplification stage but inverting the phase of the local oscillator. The resulting fields can then be probed using single-photon detectors to reveal heralded entanglement between the mode A and B. We emphasize that as the re-displacement is performed locally, it cannot increase the entanglement. A measure of the entanglement after the displacement thus provides a lower bound for the entanglement before the displacement, thus between the micro and macro states.
which ideally returns it back to the single-photon level. In practice, the de-amplification is realized in a similar manner as the amplification stage but inverting the phase of the local oscillator. The resulting fields can then be probed using single-photon detectors to reveal heralded entanglement between the mode A and B. We emphasize that as the re-displacement is performed locally, it cannot increase the entanglement. A measure of the entanglement after the displacement thus provides a lower bound for the entanglement before the displacement, thus between the micro and macro states.
The state to be measured is described by a density matrix that includes noise and loss. To reveal entanglement, we use the tomographic approach based on single-photon detections presented in ref. 6 and successfully applied in many experiments6,22,23,24. Specifically, from the measured values of the heralded probabilities pm n for detecting m photons in mode A and n in mode B (m,n∈[0,1]) and of the visibility V of the interference obtained by combining the modes A and B on a balanced beam splitter, a lower bound on the concurrence at the level of the detection is obtained through  . Let us mention that to maximize the observed concurrence, the interference visibility V needs to be maximized and the probability for having one detection in each mode, p11, has to be minimized. This can be done with ease at the single-photon level; however, as the system size increases, this becomes increasingly difficult, as we shall see in the following.
. Let us mention that to maximize the observed concurrence, the interference visibility V needs to be maximized and the probability for having one detection in each mode, p11, has to be minimized. This can be done with ease at the single-photon level; however, as the system size increases, this becomes increasingly difficult, as we shall see in the following.
The typical size that can be achieved primarily depends on the precision with which the relative phase of the local oscillators is controlled. This can be intuitively understood in two complementary ways depending on whether the phase noise is regarded as a decoherence mechanism operating on the macro state or as an imprecision of the measurement apparatus. In the first picture, a phase noise acts as if the environment performs a weak measurement of the photon number. (A phase noise, for example, the thermal fluctuations of the fibre length, can be described by a random unitary U(φ) = , where a† is the creation operator, that is applied on the state, where the random variable φ follows a normal distribution p(φ). The same transformation can be obtained if the system displaces a pointer state (associated with the environment) |ψ(p)〉E through  . After the environment is traced out such an interaction applies a random phase U(φ) on the system with probability |ψ(φ)E|2 = p(φ). What we are describing is a weak measurement of the photon number by the environmental pointer, initially in a broadened state
. After the environment is traced out such an interaction applies a random phase U(φ) on the system with probability |ψ(φ)E|2 = p(φ). What we are describing is a weak measurement of the photon number by the environmental pointer, initially in a broadened state  .) The weak measurement more easily distinguishes the two macroscopic components when |α| increases, simultaneously degrading the coherence between them. In the second picture, small imperfections in the phase of the re-displacement inevitably add noise in the detected mode. This phase noise decreases the achievable interference visibility V, and simultaneously increases p11 leading rapidly to a zero concurrence. In our set-up, the two local oscillators are produced by splitting the coherent state generated by the DFG process (see Supplementary Information). As presented in Fig. 1, both displacements are made using 90:10 beam splitters to reduce the single-photon losses, and the second unbalanced beam splitter closes a Mach–Zehnder interferometer. To accurately control and tune the relative phase between the two local oscillators, we actively stabilize the interferometer with a feedback loop locked on the side of an interference fringe using a tunable reference laser. We obtain an interference visibility of 99.985(2)%( = 1−ε) that is essentially limited by the path length difference between the two arms (∼20 μm). This translates into an extinction ratio of 1.5(2)×10−4, meaning that for |α|2 = 6,600(700), a noise of one photon is added into the detected mode. The theoretical model that we derived, which assumes that the relative phase of the two local oscillators is a stochastic variable (following a Gaussian distribution with variance 2ε), that the source produces a two-mode squeezed state, and takes optical loss, detection efficiency, pair production probability into account, predicts a positive concurrence up to |α|2 = 549, which is in excellent agreement with what we observed, as we shall see now.
.) The weak measurement more easily distinguishes the two macroscopic components when |α| increases, simultaneously degrading the coherence between them. In the second picture, small imperfections in the phase of the re-displacement inevitably add noise in the detected mode. This phase noise decreases the achievable interference visibility V, and simultaneously increases p11 leading rapidly to a zero concurrence. In our set-up, the two local oscillators are produced by splitting the coherent state generated by the DFG process (see Supplementary Information). As presented in Fig. 1, both displacements are made using 90:10 beam splitters to reduce the single-photon losses, and the second unbalanced beam splitter closes a Mach–Zehnder interferometer. To accurately control and tune the relative phase between the two local oscillators, we actively stabilize the interferometer with a feedback loop locked on the side of an interference fringe using a tunable reference laser. We obtain an interference visibility of 99.985(2)%( = 1−ε) that is essentially limited by the path length difference between the two arms (∼20 μm). This translates into an extinction ratio of 1.5(2)×10−4, meaning that for |α|2 = 6,600(700), a noise of one photon is added into the detected mode. The theoretical model that we derived, which assumes that the relative phase of the two local oscillators is a stochastic variable (following a Gaussian distribution with variance 2ε), that the source produces a two-mode squeezed state, and takes optical loss, detection efficiency, pair production probability into account, predicts a positive concurrence up to |α|2 = 549, which is in excellent agreement with what we observed, as we shall see now.
We first performed a series of measurements without displacement to verify that the modes A and B are indeed entangled when sharing a single photon. The interference fringe obtained by combining the two modes on a 50:50 beam splitter exhibits a visibility of V = 0.966(6). The conditional probabilities are measured to be p00 = 0.9719(1), p01 = 1.313(7)×10−2p10 = 1.492(8)×10−2 and p11 = 1.0(2)×10−5 leading to C≥0.0208(7). These measurements are then repeated for various displacements. Figure 2 shows the resulting concurrence. The obtained values are in excellent agreement with the theoretical model described before that uses independent measurements of the transmission loss, detection efficiencies and pair creation probability. They show that the concurrence decreases as the state describing the mode A becomes more macroscopic, and remains non-zero up to more than 500 photons. This strengthens the idea that one has to pay the price of increasing phase resolution to maintain and observe the quantum nature of a physical system as its size increases. The observed values are lower bounds on the amount of entanglement at the detection level and are mainly limited by optical loss. Factoring out the detector inefficiency and transmission loss yields an increase in the concurrence by more than one order of magnitude, for example, a lower bound of almost 20% for the concurrence of the micro–macro state with |α|2 = 100. Putting aside the loss before the displacement (the coupling inefficiency of the idler photon into the fibre), the concurrence would further increase to around 40% for |α|2 = 100.
We have reported an experimental observation of heralded entanglement involving two components that could be distinguished with detectors resolving only large photon number differences. Although there is no consensus on the definition of macroscopic entanglement, we believe that this property captures the essence of what is a genuinely macroscopic quantum state. Similarly to NOON states25 or squeezed states26, the phase sensitivity of the macro state under consideration may be useful for precision measurements, especially in the presence of loss, where alternative states have a limited usefulness. Returning to a more fundamental perspective, one could imagine mapping these superpositions into the motion of a massive object by momentum transfer. This could open up the possibility of testing unconventional decoherence models.
References
Brune, M. et al. Observing the progressive decoherence of the ‘Meter’ in a quantum measurement. Phys. Rev. Lett. 77, 4887–4890 (1996).
Monroe, C., Meekhof, D. M., King, B. E. & Wineland, D. J. A Schrodinger cat superposition state of an atom. Science 272, 1131–1136 (1996).
Turchette, Q. A. et al. Decoherence and decay of motional quantum states of a trapped atom coupled to engineered reservoirs. Phys. Rev. A 62, 053807 (2000).
Sekatski, P., Sangouard, N. & Gisin, N. The size of quantum superpositions as measured with ‘classical’ detectors. Preprint at http://arxiv.org/abs/1306.0843 (2013).
Sekatski, P. et al. Proposal for exploring macroscopic entanglement with a single photon and coherent states. Phys. Rev. A 86, 060301 (2012).
Chou, C. W. et al. Measurement-induced entanglement for excitation stored in remote atomic ensembles. Nature 438, 828–832 (2005).
Zurek, W. H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 75, 715–775 (2003).
Sekatski, P., Sanguinetti, B., Pomarico, E., Gisin, N. & Simon, C. Cloning entangled photons to scales one can see. Phys. Rev. A 82, 053814 (2010).
Sekatski, P., Brunner, N., Branciard, C., Gisin, N. & Simon, C. Towards quantum experiments with human eyes as detectors based on cloning via stimulated emission. Phys. Rev. Lett. 103, 113601 (2009).
Spagnolo, N., Vitelli, C., Sciarrino, F. & De Martini, F. Entanglement criteria for microscopic-macroscopic systems. Phys. Rev. A 82, 052101 (2010).
Spagnolo, N., Vitelli, C., Paternostro, M., De Martini, F. & Sciarrino, F. Hybrid methods for witnessing entanglement in a microscopic-macroscopic system. Phys. Rev. A 84, 032102 (2011).
De Martini, F. & Sciarrino, F. Investigating macroscopic quantum superpositions and the quantum-to-classical transition by optical parametric amplification. Preprint at http://arxiv.org/abs/1202.5518 (2012).
De Martini, F., Sciarrino, F. & Vitelli, C. Entanglement test on a microscopic-macroscopic system. Phys. Rev. Lett. 100, 253601 (2008).
Mermin, N. Quantum mechanics vs local realism near the classical limit: A Bell inequality for spin s. Phys. Rev. D 22, 356–361 (1980).
Peres, A. Quantum Theory: Concepts and Methods (Klouwer, 2002).
Christ, A., Laiho, K., Eckstein, A., Cassemiro, K. N. & Silberhorn, C. Probing multimode squeezing with correlation functions. New J. Phys. 13, 033027 (2011).
Asbóth, J., Calsamiglia, J. & Ritsch, H. Computable measure of nonclassicality for light. Phys. Rev. Lett. 94, 173602 (2005).
Solomon Ivan, J., Mukunda, N. & Simon, R. Generation and distillation of non-Gaussian entanglement from nonclassical photon statistics. Quant. Inf. Process. 11, 873–885 (2011).
Paris, M. G. Displacement operator by beam splitter. Phys. Lett. A 217, 78–80 (1996).
Lvovsky, A. & Babichev, S. Synthesis and tomographic characterization of the displaced Fock state of light. Phys. Rev. A 66, 1–4 (2002).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Choi, K. S., Deng, H., Laurat, J. & Kimble, H. J. Mapping photonic entanglement into and out of a quantum memory. Nature 452, 67–71 (2008).
Usmani, I. et al. Heralded quantum entanglement between two crystals. Nature Photon. 6, 234–237 (2012).
Lee, K. C. et al. Entangling macroscopic diamonds at room temperature. Science 334, 1253–1256 (2011).
Afek, I., Ambar, O. & Silberberg, Y. High-NOON states by mixing quantum and classical light. Science 328, 879–881 (2010).
The LIGO Scientific Collaboration, A gravitational wave observatory operating beyond the quantum shot-noise limit. Nature Phys. 7, 962–965 (2011).
Acknowledgements
We thank B. Sanguinetti and H. Zbinden for stimulating discussions and IDQ for the loan of ID210 detectors. This work was supported in part by the EU project Q-Essence and the Swiss SNSF project—CR23I2 127118.
Author information
Authors and Affiliations
Contributions
A.M., N.S. and R.T.T. conceived and designed the research. N.B. and A.M. carried out the experiment. P.S. and N.S. contributed with theoretical analysis. All authors participated in writing the manuscript. N.S., R.T.T. and N.G. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 261 kb)
Rights and permissions
About this article
Cite this article
Bruno, N., Martin, A., Sekatski, P. et al. Displacement of entanglement back and forth between the micro and macro domains. Nature Phys 9, 545–548 (2013). https://doi.org/10.1038/nphys2681
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2681
This article is cited by
-
Entangled states shaping with CV states of definite parity
Scientific Reports (2022)
-
Micro–micro and micro–macro entanglement witnessing via the geometric phase in an impurity-doped Bose–Einstein condensate
Quantum Information Processing (2022)
-
Enhancing Non-classicality By Superposing Two Induced States From Coherent States
International Journal of Theoretical Physics (2022)
-
Efficient production of large-size optical Schrödinger cat states
Scientific Reports (2019)
-
Designs of interactions between discrete- and continuous-variable states for generation of hybrid entanglement
Quantum Information Processing (2019)