Abstract
Harnessing spins as information carriers has emerged as an elegant extension to the transport of electrical charges1. The coherence of such spin transport in spintronic circuits is determined by the lifetime of spin excitations and by spin diffusion. Fermionic quantum gases allow the study of spin transport from first principles because interactions can be precisely tailored and the dynamics is on directly observable timescales2,3,4,5,6,7,8,9,10,11,12. In particular, at unitarity, spin transport is dictated by diffusion and the spin diffusivity is expected to reach a universal, quantum-limited value on the order of the reduced Planck constant ħ divided by the mass m. Here, we study a two-dimensional Fermi gas after a quench into a metastable, transversely polarized state. Using the spin-echo technique13, for strong interactions, we measure the lowest transverse spin diffusion constant14,15 so far 6.3 (8) × 10-3 ħ/m. For weak interactions, we observe a collective transverse spin-wave mode that exhibits mode softening when approaching the strongly interacting regime.
Similar content being viewed by others
Main
Studying transport in low-dimensional nanostructures has a long and rich history because of its non-trivial features and its relevance for electronic devices. The most common case, charge transport, has great technological implications and determines the current–voltage characteristics of a device. With the development of the field of spintronics1, however, spin transport has also moved into the focus of the research interest. Spin transport has unique properties, setting it aside from charge transport: first, the transport of spin polarization is not protected by momentum conservation and is greatly affected by scattering5,16. Therefore, the question arises: what is the limiting case of the spin transport coefficients when interactions reach the maximum value allowed by quantum mechanics? Second, unlike charge currents (which lead to charge separation and the buildup of an electrical field, counteracting the current), spin accumulation does not induce a counteracting force.
The main mechanism to even out a non-equilibrium magnetization M(r,t) = M(r,t)p(r,t) is spin diffusion, which is an overall spin-conserving process. Other, non-spin-conserving processes are much slower in ultracold Fermi gas experiments and are neglected hereafter. The gradient of the non-equilibrium magnetization  drives two distinct spin currents17: The first term produces a longitudinal spin current and the second term induces a transverse spin current. These spin currents are proportional to the longitudinal
drives two distinct spin currents17: The first term produces a longitudinal spin current and the second term induces a transverse spin current. These spin currents are proportional to the longitudinal  and transverse
and transverse  spin diffusivity, respectively.
spin diffusivity, respectively.
In general, the spin diffusivity in D dimensions behaves as  , where v is the collision velocity, n is the density and σ is the elastic scattering cross section between atoms. For short-range s-wave interactions at unitarity, the cross section attains its maximum value allowed by quantum mechanics σ∼λdBD−1, where degenerate regime (of any dimensionality) the de Broglie wavelength λdB is of the order of 1/kF and hence the mean-free path is lmfp = 1/(n σ)≈1/kF, where kF is the Fermi wave vector of the gas and n∼kFD is the density. Hence, the spin diffusion constant is given by ℏ/m. This quantum limit can also be viewed as a result of the uncertainty principle by noticing that the mean-free path lmfp = 1/n σ is limited by the mean interparticle spacing11. The simple scaling argument, however, hides much of the rich underlying physics. In particular, it cannot explain the Leggett–Rice effect14,15,18, the difference between longitudinal and transverse spin diffusivities19, and the transition to weak interactions where the physics changes because the system evolves from collision-dominated to collisionless. The lowest spin diffusion constant for longitudinal spin currents has been measured to be
, where v is the collision velocity, n is the density and σ is the elastic scattering cross section between atoms. For short-range s-wave interactions at unitarity, the cross section attains its maximum value allowed by quantum mechanics σ∼λdBD−1, where degenerate regime (of any dimensionality) the de Broglie wavelength λdB is of the order of 1/kF and hence the mean-free path is lmfp = 1/(n σ)≈1/kF, where kF is the Fermi wave vector of the gas and n∼kFD is the density. Hence, the spin diffusion constant is given by ℏ/m. This quantum limit can also be viewed as a result of the uncertainty principle by noticing that the mean-free path lmfp = 1/n σ is limited by the mean interparticle spacing11. The simple scaling argument, however, hides much of the rich underlying physics. In particular, it cannot explain the Leggett–Rice effect14,15,18, the difference between longitudinal and transverse spin diffusivities19, and the transition to weak interactions where the physics changes because the system evolves from collision-dominated to collisionless. The lowest spin diffusion constant for longitudinal spin currents has been measured to be  in three-dimensional (3D) degenerate Fermi gases at unitarity5, approximately two orders of magnitude smaller than in semiconductor nanostructures16.
in three-dimensional (3D) degenerate Fermi gases at unitarity5, approximately two orders of magnitude smaller than in semiconductor nanostructures16.
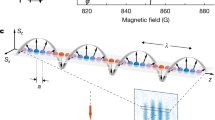
Here, we study the coherence properties of a transversely polarized 2D Fermi gas under the influence of a magnetic field gradient. By employing the spin-echo technique13 we gain access to the intriguing, but little understood, transverse spin dynamics in 2D Fermi systems17. The experiment starts by producing a Fermi gas of 40K atoms. The motion of the atoms is restricted to a 2D plane20,21 by an optical lattice of wavelength λ = 1,064 nm, with the radial confinement being harmonic with a trap frequency of ωr = 2π×127 Hz. After production of a spin-polarized, 2D gas, we apply three resonant radio-frequency pulses to rotate the spin state by respective angles π/2−π−π/2 about the Sx-axis in spin space. Consecutive pulses are separated by a time τ and we refer to the spin evolution time as t = 2τ. The initial π/2-pulse creates transverse spin polarization in a coherent superposition between  and
and  (Fig. 1). An applied magnetic field gradient B′≡∂ Bz/∂ x gives rise to a transverse spin wave of wave vector Q = δ γ t B′, where δ γ = 2π × 152 kHz G-1 is the difference of the gyromagnetic ratio for
(Fig. 1). An applied magnetic field gradient B′≡∂ Bz/∂ x gives rise to a transverse spin wave of wave vector Q = δ γ t B′, where δ γ = 2π × 152 kHz G-1 is the difference of the gyromagnetic ratio for  and
and  at 209.15 G and t is the evolution time (see Methods). On timescales much shorter than the trapping period, Q is independent of the interaction strength22, and nearby atoms acquire a relative phase angle of Δϕ≈Q/kF. This lifts the spin polarization of the Fermi gas and the spins can collide with each other as they move in the harmonic potential or diffuse. Trivial dephasing induced by the magnetic field gradient is reversed by the π-pulse and the spin state refocuses after a time τ if no decoherence has occurred. The final π/2-pulse maps the spin state from Sy onto Sz, which is measured by performing a Stern–Gerlach experiment in time of flight, and we record 〈Mz〉 = (N↑−N↓)/(N↑+N↓), where N↓/↑ is the total number of spin down/up atoms.
at 209.15 G and t is the evolution time (see Methods). On timescales much shorter than the trapping period, Q is independent of the interaction strength22, and nearby atoms acquire a relative phase angle of Δϕ≈Q/kF. This lifts the spin polarization of the Fermi gas and the spins can collide with each other as they move in the harmonic potential or diffuse. Trivial dephasing induced by the magnetic field gradient is reversed by the π-pulse and the spin state refocuses after a time τ if no decoherence has occurred. The final π/2-pulse maps the spin state from Sy onto Sz, which is measured by performing a Stern–Gerlach experiment in time of flight, and we record 〈Mz〉 = (N↑−N↓)/(N↑+N↓), where N↓/↑ is the total number of spin down/up atoms.
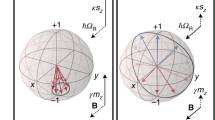
a, A π/2-pulse prepares the Fermi gas polarized in the Sy-direction. b, A magnetic field gradient ∂ Bz/∂ x causes the spins to acquire different phase angles ϕ(x) in the equatorial plane. c, Collisions tilt the spins out of the equatorial plane owing to the identical spin-rotation effect. The acquired projection along Sz, together with the motion of the atoms in the harmonic trap, impedes rephasing of the spins when the magnetic field gradient is reversed. The spin states are shown in the rotating frame.
Even though the interaction potential between atoms is not explicitly spin dependent, an effective spin-exchange interaction is mediated by the required anti-symmetrization of the scattering wave function because of Pauli’s exclusion principle. In binary collisions, this leads to the identical spin-rotation effect23: in a collision both spins rotate about the axis defined by the sum of their spin orientations. In the Fermi degenerate regime, the binary collision picture has to be replaced by Landau’s quasiparticle description. Here, quasiparticle excitations are restricted to near the Fermi surface and can be considered as being affected by a ‘molecular field’ resulting from the effective spin-exchange interaction14,15,24,25. As a result, the spin wave cants out of the Sx–Sy-plane and forms a spin spiral which acquires a component along Sz (see Fig. 1c). The magnitude of the identical spin-rotation effect is proportional to the mean-field interaction strength g = −2πℏ2/[mln(kFa2D)]of the gas26. Here, kF is the Fermi wave vector for the initially spin-polarized sample and a2D is the 2D scattering length (see Methods). We perform the experiment near the Feshbach resonance at 202.1 G, which allows tuning the strength of the interaction.
In the strongly interacting regime, that is, −1<ln(kFa2D)<3, spin transport is dominated by diffusion and the spin-echo signal attains a characteristic non-exponential decay of the form13,14,15  . Fitting the envelope of the spin-echo signal (see Fig. 2a) with this function allows us to deduce the transverse spin diffusion constant. (Our experimental timing is not phase stable with respect to the Larmor precession of ≈50 MHz. Hence, our analysis focusses on the envelope of the spin echo, from which the shown data points typically scatter less than 10%. The combined error of preparation and detection of the magnetization for a single data point is less than 1%.) We extract the transverse spin diffusion constant for various interaction strengths and find
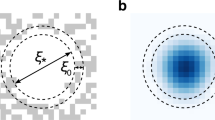
. Fitting the envelope of the spin-echo signal (see Fig. 2a) with this function allows us to deduce the transverse spin diffusion constant. (Our experimental timing is not phase stable with respect to the Larmor precession of ≈50 MHz. Hence, our analysis focusses on the envelope of the spin echo, from which the shown data points typically scatter less than 10%. The combined error of preparation and detection of the magnetization for a single data point is less than 1%.) We extract the transverse spin diffusion constant for various interaction strengths and find  at a shallow minimum around ln(kFa2D) = 0 (Fig. 2b). From the arguments given above, we expect the diffusivity to be on the order of ℏ/m. Observing a smaller value than for longitudinal spin diffusion in three dimensions5 is possibly less linked to the dimensionality rather than to the phase space available for collisions necessary to drive spin diffusion19: In the case of longitudinal spin currents, a gradient of the Mz(x) polarization along the x-direction can be considered as a spatial variation of the local Fermi surfaces kF,↑(x) and kF,↓(x) (Fig. 2c). Only
at a shallow minimum around ln(kFa2D) = 0 (Fig. 2b). From the arguments given above, we expect the diffusivity to be on the order of ℏ/m. Observing a smaller value than for longitudinal spin diffusion in three dimensions5 is possibly less linked to the dimensionality rather than to the phase space available for collisions necessary to drive spin diffusion19: In the case of longitudinal spin currents, a gradient of the Mz(x) polarization along the x-direction can be considered as a spatial variation of the local Fermi surfaces kF,↑(x) and kF,↓(x) (Fig. 2c). Only  spins in a small region near the Fermi surface can diffuse from x to x+dx, invoking the typical T−2 scaling for quasiparticles in the deeply degenerate regime. In contrast, in the case of transverse spin currents the Fermi surfaces at different positions are of the same size but have slightly different directions of magnetization (see Fig. 2d). Hence, a spin moving along x from anywhere between the Fermi surfaces for spin-up and spin-down must scatter to reach local equilibrium, which scales as n↑−n↓ and provides a much larger phase space. The result is that for a degenerate system the transverse diffusivity is smaller than the longitudinal one and becomes independent of temperature19.
spins in a small region near the Fermi surface can diffuse from x to x+dx, invoking the typical T−2 scaling for quasiparticles in the deeply degenerate regime. In contrast, in the case of transverse spin currents the Fermi surfaces at different positions are of the same size but have slightly different directions of magnetization (see Fig. 2d). Hence, a spin moving along x from anywhere between the Fermi surfaces for spin-up and spin-down must scatter to reach local equilibrium, which scales as n↑−n↓ and provides a much larger phase space. The result is that for a degenerate system the transverse diffusivity is smaller than the longitudinal one and becomes independent of temperature19.
a, Transverse spin diffusion constant  as a function of interaction strength deduced from the decay constant Γ of the spin-echo signal. The error bars denote the 1σ uncertainty of the fit. Inset: spin-echo signal at ln(kFa2D) = −0.2. The blue line is a fit ∝exp[−(2Γτ)3]. b,c, Illustration of the different spatial variation of Fermi surfaces of a polarized Fermi gas for the case of longitudinal (b) and transverse (c) spin diffusion.
as a function of interaction strength deduced from the decay constant Γ of the spin-echo signal. The error bars denote the 1σ uncertainty of the fit. Inset: spin-echo signal at ln(kFa2D) = −0.2. The blue line is a fit ∝exp[−(2Γτ)3]. b,c, Illustration of the different spatial variation of Fermi surfaces of a polarized Fermi gas for the case of longitudinal (b) and transverse (c) spin diffusion.
In the weakly interacting attractive Fermi liquid regime27, that is, ln(kFa2D)>3, we observe a qualitatively different behaviour (Fig. 3a). The envelope of the spin-echo signal decays exponentially and is modulated by a slow oscillation, and both the frequency and the damping constant of the oscillation depend on the interaction strength. We attribute this slow periodic modulation to transverse spin waves which are excited by the spin-echo sequence. The spin current induced by the magnetic field gradient can only be inverted completely by the π-pulse when applied in phase with the harmonic motion. This can be qualitatively (for zero interactions) understood in a phase-space picture by considering that the magnetic field gradient causes a spatial offset between the potentials for the  and the
and the  spin states and, correspondingly, the phase-space trajectories of the two spin components are displaced9. Indeed, we observe that the difference of the centre-of-mass momenta 〈k↑〉−〈k↓〉 of the two spin densities n↑(k) and n↓(k) oscillates out-of-phase with the contrast of the spin-echo signal (Fig. 3a,b). The total density profile n(k) = n↑(k)+n↓(k) is stationary, which indicates a pure spin mode.
spin states and, correspondingly, the phase-space trajectories of the two spin components are displaced9. Indeed, we observe that the difference of the centre-of-mass momenta 〈k↑〉−〈k↓〉 of the two spin densities n↑(k) and n↓(k) oscillates out-of-phase with the contrast of the spin-echo signal (Fig. 3a,b). The total density profile n(k) = n↑(k)+n↓(k) is stationary, which indicates a pure spin mode.
 ).
).a, Envelope of the spin-echo signal (dots) and the fit function (blue line). b, Centre of mass separation of  and
and  after a time of flight of 11.8 ms. The shaded area is a series of Gaussians repeated at the same period and with the same exponential decay as the oscillations in a. c,d, Momentum distribution of local spin polarization for large and small spin polarization, positions marked by the circles c and d on a, respectively. The lower two panels in d show the distribution of spin up and spin down, respectively.
after a time of flight of 11.8 ms. The shaded area is a series of Gaussians repeated at the same period and with the same exponential decay as the oscillations in a. c,d, Momentum distribution of local spin polarization for large and small spin polarization, positions marked by the circles c and d on a, respectively. The lower two panels in d show the distribution of spin up and spin down, respectively.
The measured envelope of the spin-echo signal (Fig. 3a) is fitted with an empirical function of the form: A exp(−γ t)(1−B|sin(ω t/2)|3)+C. Here,  and |C|≪1 are amplitudes and a global offset of the spin-echo signal, respectively. This fit function reproduces the non-sinusodial signal shape and allows us to extract the oscillation frequency ω and amplitude decay γ. The exact shape can be calculated analytically only in the case of vanishing interactions9. The exponent is fixed to the value 3 for all interactions and we do not observe a systematic dependence of the deduced frequencies and damping rates on the exact choice of the exponent.
and |C|≪1 are amplitudes and a global offset of the spin-echo signal, respectively. This fit function reproduces the non-sinusodial signal shape and allows us to extract the oscillation frequency ω and amplitude decay γ. The exact shape can be calculated analytically only in the case of vanishing interactions9. The exponent is fixed to the value 3 for all interactions and we do not observe a systematic dependence of the deduced frequencies and damping rates on the exact choice of the exponent.
For zero interaction strength the mode is at half the trap frequency and we observe a softening of the spin mode when approaching the strongly interacting, collision-dominated regime (Fig. 4a,b). This shows that for strong interactions the spin-wave dynamics is superseded by spin diffusion. Such a behaviour is reminiscent of the collisionless to collision-dominated transition of the spin-dipole oscillation5,28. The decay rate γ of the oscillation (see Fig. 4c) is smallest for the non-interacting gas, where it is two orders of magnitude smaller than the dephasing rate 1/τRamsey in the inhomogeneous magnetic field (see Methods). As the interaction strength is increased, the rate γ is growing. We fit this growth with a power-law behaviour γ = α/ln(kFa2D)β+γ0 and determine the exponent to be β = 1.3±0.15. Observing a scaling with an exponent close to unity signals that the loss of global coherence is dominated by the identical spin-rotation effect, which scales proportionally to the mean-field interaction strength g. In contrast, the rate of elastic collisions scales as ∝1/ln(kFa2D)2, that is, β = 2. This suggest the following decoherence mechanism in a spin-1/2 Fermi gas: after building up in the magnetic field gradient, the spin wave decays when neighbouring atoms have acquired a sufficiently large phase angle Δϕ between their spins such that in a spin-conserving collision both spins rotate out of the Sx–Sy-plane. Initially, this is a coherent process, which subsequently dephases due to the coupling of the spin rotation to the momentum of the atoms29. Our spin-echo measurements show that the dephasing time measured by the Ramsey technique underestimates the actual spin decoherence time in the weakly interacting regime by orders of magnitude.
a, Time evolution of the global spin polarization for different interaction strengths. b, Frequency of oscillating spin polarization. For the data points at ln(kFa2D) = 3 and below we were not able to fit a frequency. c, Damping coefficient γ of the spin polarization. The dashed line indicates the elastic scattering rate (β = 2) and the solid line is a fit to the measured decay (β = 1.3±0.15). The error bars denote the 1σ uncertainty of the fits
In strongly interacting ultracold atomic gases and condensed-matter systems in which spin-relaxation processes are suppressed, spin diffusion is the dominant process to equilibrate a non-equilibrium spin polarization. The search for a quantum-mechanical bound on spin diffusivity has been ongoing in various systems5,16,17,19, and here we have reported the lowest yet spin diffusion constant of 6.3(8) × 10-3 ℏ/m. Our work could pave the way towards an alternative mechanism to form ferromagnetic states of strongly repulsively interacting Fermi gases22.
Methods
Preparation of the 2D gases.
We prepare a quantum degenerate Fermi gas of 40K atoms in a one-dimensional optical lattice of wavelength λ = 1,064 nm populating a stack of approximately 40 individual 2D quantum gases21,30. The radial confinement of the 2D gases is harmonic with a trap frequency of ωr = 2π×127 Hzand the axial trap frequency is ωz = 2π×75 kHz. Using a radio-frequency cleaning pulse, we ensure preparation of a spin-polarized gas in the  ground state with 1.5×105 atoms, corresponding to a density-averaged Fermi energy of the spin-polarized gas EF = h × 12.3(5) kHz at a temperature of kBT/EF = 0.24(3). Our experiments on the spin dynamics start by ramping the magnetic field from B = 209.15 G to the desired value B near the Feshbach resonance in 30 ms, and then waiting there for 200 ms. Subsequently, we apply the spin-echo pulse sequence (see main text) of three radio-frequency pulses with frequencies of ∼ 50 MHz. The pulses have square envelopes and durations of tπ/2∼46 μs for a π/2-pulse and 2×tπ/2 for a π-pulse. The pulses are separated by equal times τ, which gives a total spin evolution time t = 2τ.
ground state with 1.5×105 atoms, corresponding to a density-averaged Fermi energy of the spin-polarized gas EF = h × 12.3(5) kHz at a temperature of kBT/EF = 0.24(3). Our experiments on the spin dynamics start by ramping the magnetic field from B = 209.15 G to the desired value B near the Feshbach resonance in 30 ms, and then waiting there for 200 ms. Subsequently, we apply the spin-echo pulse sequence (see main text) of three radio-frequency pulses with frequencies of ∼ 50 MHz. The pulses have square envelopes and durations of tπ/2∼46 μs for a π/2-pulse and 2×tπ/2 for a π-pulse. The pulses are separated by equal times τ, which gives a total spin evolution time t = 2τ.
Interactions in two dimensions.
For 2D scattering with relative momentum q, the amplitude of the outgoing cylindrical wave for low-energy scattering is31 f(q) = 4π/[ln(1/q2a2D2)+iπ]. This defines the 2D scattering length a2D, which is linked to the binding energy of the confinement-induced dimer by EB = ℏ2/m a2D2. The logarithmic dependence of the scattering amplitude on momentum shows that f(q) is never independent of energy. In the regime of many-body physics of the weakly interacting 2D Fermi gas, the coupling strength is parameterized by the coefficient26 g = −2πℏ2/[m ln(kFa2D)]. The regime of zero interaction corresponds to  , which is qualitatively different from the three-dimensional case, where an infinite scattering length is observed in the regime of strongest interaction. In contrast, in two dimensions the regime of strongest interaction arises for ln(kFa2D) = 0, as according to the optical theorem the two-body scattering cross section σ = −Im[f(q)]/q = 4/q attains the maximal possible value dictated by unitarity, which is essentially the de-Broglie wavelength. In the strongly interacting regime the mean field expansion in powers of 1/ln(kFa2D) breaks down. Instead, the energy per particle, after subtracting the two-body bound state energy, approaches a universal value32 0.204 EF/2.
, which is qualitatively different from the three-dimensional case, where an infinite scattering length is observed in the regime of strongest interaction. In contrast, in two dimensions the regime of strongest interaction arises for ln(kFa2D) = 0, as according to the optical theorem the two-body scattering cross section σ = −Im[f(q)]/q = 4/q attains the maximal possible value dictated by unitarity, which is essentially the de-Broglie wavelength. In the strongly interacting regime the mean field expansion in powers of 1/ln(kFa2D) breaks down. Instead, the energy per particle, after subtracting the two-body bound state energy, approaches a universal value32 0.204 EF/2.
Ramsey measurements: dephasing in the magnetic field gradient.
We assess the timescale of simple dephasing of the spin in the magnetic field gradient by performing Ramsey spectroscopy on the non-interacting gas using the following sequence: the initial π/2-pulse is followed by a second π/2-pulse with a variable time delay τ. We observe a Ramsey coherence time of τRamsey = (600±30)μs. As the Ramsey time is more than an order of magnitude shorter than the inverse trap frequency, we neglect the motional contribution to the dephasing. Instead, we relate the Ramsey time to the dephasing time of the (quasi stationary) spins across the whole cloud, and we find from this the magnetic field gradient. Assuming a Thomas–Fermi distribution of atoms in the 2D potential, we fit the data with P(t) = 8J2(ϕ)/ϕ2, where J2 is the Bessel function of the first kind. The phase shift between the centre and the edge of the cloud, that is, the Fermi radius RF, is ϕ = δ γ B′RFt. The difference of the gyromagnetic factors, δ γ(B), is a function of the magnetic field and defined as the difference between the derivative of the Zeeman energies for the two spin states, that is, ℏδ γ(B) = ∂ E−9/2/∂ B|B−∂ E−7/2/∂ B|B. From a nonlinear least-squares fit we deduce B′ = 4.7(2) G cm−1 for RF = 17.7(5) μm and δ γ(209.15 G) = 2π × 152 kHz G−1.
Change history
04 June 2013
In the version of this Letter originally published online, in the third main paragraph, the formula for the maximum elastic scattering cross section between atoms should have read σ∼λdBD−1. In the previous paragraph, penultimate sentence, the terms 'parallel to M' and 'orthogonal to M' should not have been included. In the section 'Interactions in two dimensions', the first equation should have included square brackets, as here: f(q) = 4π/[ln(1/q2a2D2)+iπ]. These corrections have been made in the HTML and PDF versions of the Letter.
23 December 2013
In the version of this Letter originally published, the stated value for the difference in the gyromagnetic ratio for the |↑> and |↓> state, δγ, was missing a factor of 2π. Consequently, the diffusion constants were overestimated by a factor of (2π)2. In particular, the value at ln(kFa2D) = 0 stated in the text should be 6.3(8) × 10-3ħ/m instead of 0.25(3)ħ/m. Other quantities, such as the magnetic field gradient, which was independently calibrated, are not affected. All other statements and observations in the published version are correct and remain unaffected. These errors have now been corrected in the online versions of the Letter.
References
Awschalom, D. D., Loss, D. & Samarth, N. (eds) Semiconductor Spintronics and Quantum Computation (NanoScience and Technology, Springer, 2007).
Gensemer, S. D. & Jin, D. S. Transition from collisionless to hydrodynamic behavior in an ultracold Fermi gas. Phys. Rev. Lett. 87, 173201 (2001).
Du, X., Luo, L., Clancy, B. & Thomas, J. E. Observation of anomalous spin segregation in a trapped Fermi gas. Phys. Rev. Lett. 101, 150401 (2008).
Du, X., Zhang, Y., Petricka, J. & Thomas, J. E. Controlling spin current in a trapped Fermi gas. Phys. Rev. Lett. 103, 010401 (2009).
Sommer, A., Ku, M., Roati, G. & Zwierlein, M. W. Universal spin transport in a strongly interacting Fermi gas. Nature 472, 201–204 (2011).
Sommer, A., Ku, M. & Zwierlein, M. W. Spin transport in polaronic and superfluid Fermi gases. New J. Phys. 13, 055009 (2011).
Bruun, G. M. Spin diffusion in Fermi gases. New J. Phys. 13, 035005 (2011).
Wulin, D., Guo, H., Chien, C-C. & Levin, K. Spin transport in cold Fermi gases: A pseudogap interpretation of spin diffusion experiments at unitarity. Phys. Rev. A 83, 061601 (2011).
Ebling, U., Eckardt, A. & Lewenstein, M. Spin segregation via dynamcially induced long-range interactions in a system of ultracold fermions. Phys. Rev. A 84, 063607 (2011).
Bruun, G. M. Shear viscosity and spin-diffusion coefficient of a 2D Fermi gas. Phys. Rev. A 85, 013636 (2012).
Enss, T., Küppersbusch, C. & Fritz, L. Shear viscosity and spin diffusion in a 2D Fermi gas. Phys. Rev. A 86, 013617 (2012).
Enss, T. & Haussmann, R. Quantum mechanical limitations to spin diffusion in the unitary Fermi gas. Phys. Rev. Lett. 109, 195303 (2012).
Hahn, E. L. Spin echoes. Phys. Rev. 80, 580–594 (1950).
Leggett, A. J. & Rice, M. J. Spin echoes in liquid 3H and mixtures: A predicted new effect. Phys. Rev. Lett. 20, 586–589 (1968).
Leggett, A. J. Spin diffusion and spin echoes in liquid 3H at low temperature. J. Phys. C 3, 448 (1970).
Weber, C. P. et al. Observation of spin Coulomb drag in a 2D electron gas. Nature 437, 1330–1333 (2005).
Dobbs, E. R. Helium Three (Oxford Univ. Press, 2000).
Corruccini, L. R., Osheroff, D. D., Lee, D. M. & Richardson, R. C. Spin diffusion in liquid 3He: The effect of Leggett and Rice. Phys. Rev. Lett. 27, 650–653 (1971).
Mullin, W. J. & Jeon, J. W. Spin diffusion in dilute, polarized 3He–4He solutions. J. Low Temp. Phys. 88, 433–482 (1992).
Martiyanov, K., Makhalov, V. & Turlapov, A. Observation of a 2D Fermi gas of atoms. Phys. Rev. Lett. 105, 030404 (2010).
Fröhlich, B. et al. Radiofrequency spectroscopy of a strongly interacting 2D Fermi gas. Phys. Rev. Lett. 106, 105301 (2011).
Conduit, G. J. & Altman, E. Dynamical instability of a spin spiral in an interacting Fermi gas as a probe of the Stoner transition. Phys. Rev. A 82, 043603 (2010).
Lhuillier, C & Laloë, F Transport properties in a spin polarized gas, II. J. Phys. France 43, 225–241 (1982).
Silin, V. Oscillations of a Fermi-liquid in a magnetic field. Sov. Phys. JETP 6, 945–950 (1958).
Lévy, L. P. & Ruckenstein, A. E. Collective spin oscillations in spin-polarized gases: Spin-polarized hydrogen. Phys. Rev. Lett. 52, 1512–1515 (1984).
Bloom, P. Two-dimensional Fermi gas. Phys. Rev. B 12, 125 (1975).
Fröhlich, B. et al. Two-dimensional Fermi liquid with attractive interactions. Phys. Rev. Lett. 109, 130403 (2012).
Vichi, L. & Stringari, S. Collective oscillations of an interacting trapped Fermi gas. Phys. Rev. A 60, 4734 (1999).
Fuchs, J. N., Gangardt, D. M. & Laloë, F. Internal state conversion in ultracold gases. Phys. Rev. Lett. 88, 230404 (2002).
Feld, M., Fröhlich, B., Vogt, E., Koschorreck, M. & Köhl, M. Observation of a pairing pseudogap in a 2D Fermi gas. Nature 480, 75–78 (2011).
Petrov, D. & Shlyapnikov, G. Interatomic collisions in a tightly confined Bose gas. Phys. Rev. A 64, 012706 (2001).
Bertaina, G. & Giorgini, S. BCS–BEC crossover in a 2D Fermi gas. Phys. Rev. Lett. 106, 110403 (2011).
Acknowledgements
We thank E. Altman, G. Conduit, E. Demler, U. Ebling, A. Eckardt, C. Kollath, M. Lewenstein, A. Recati and W. Zwerger for discussions and B. Fröhlich and M. Feld for contributions to the experimental apparatus. The work has been supported by EPSRC (EP/J01494X/1, EP/K003615/1), the Leverhulme Trust (M. Koschorreck), the Royal Society, the Wolfson Foundation, and the Alexander-von-Humboldt Professorship.
Author information
Authors and Affiliations
Contributions
The measurements were conceived by M. Koschorreck and M. Köhl, data were taken by M. Koschorreck, D.P., and E.V., data analysis and writing of the manuscript was performed by M. Koschorreck and M. Köhl.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Koschorreck, M., Pertot, D., Vogt, E. et al. Universal spin dynamics in two-dimensional Fermi gases. Nature Phys 9, 405–409 (2013). https://doi.org/10.1038/nphys2637
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2637
This article is cited by
-
Tunable itinerant spin dynamics with polar molecules
Nature (2023)
-
Long-lived phantom helix states in Heisenberg quantum magnets
Nature Physics (2022)
-
Spectroscopic probes of quantum gases
Nature Physics (2021)
-
Observation of spin-space quantum transport induced by an atomic quantum point contact
Nature Communications (2021)
-
Spin transport in a tunable Heisenberg model realized with ultracold atoms
Nature (2020)