Abstract
When two indistinguishable single photons impinge at the two inputs of a beam splitter they coalesce into a pair of photons appearing in either one of its two outputs. This effect is due to the bosonic nature of photons and was first experimentally observed by Hong, Ou and Mandel1. Here, we present the observation of the Hong–Ou–Mandel effect with two independent single-photon sources in the microwave frequency domain. We probe the indistinguishability of single photons, created with a controllable delay, in time-resolved second-order cross- and auto-correlation function measurements. Using quadrature amplitude detection we are able to resolve different photon numbers and detect coherence in and between the output arms. This scheme allows us to fully characterize the two-mode entanglement of the spatially separated beam-splitter output modes. Our experiments constitute a first step towards using two-photon interference at microwave frequencies for quantum communication and information processing2,3,4,5.
Similar content being viewed by others
Main
So far, Hong–Ou–Mandel (HOM) two-photon interference has been demonstrated exclusively using photons at optical or telecom wavelengths. Experiments were performed with photons emitted from a single source using parametric downconversion1, trapped ions3, atoms6, quantum dots7 and single molecules8. The HOM effect has also been observed with two independent sources9,10,11,12,13,14,15 realizing indistinguishable single-photon states, which are required as a resource in quantum networks or linear-optics quantum computation. Such experiments have also been performed using donor impurities as sources16 including nitrogen–vacancy centres in diamond (see ref. 17 and references therein). Furthermore, the HOM effect has been employed to create entanglement between ions18 in spatially separated traps, and to realize a controlled-NOT gate in a small-scale photonic network19. Similar physics is also actively explored with ballistic electrons in solids (see ref. 20 and references therein).
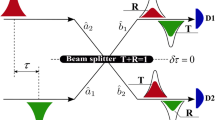
Here, we demonstrate the HOM interference of two indistinguishable microwave photons emitted from independent triggered sources realized in superconducting circuits (see Methods). The photons are prepared in two separate microwave resonators A (B) using transmon-type qubits and decay exponentially at rates κ/2π = 4.1 (4.6) MHz through their strongly coupled output ports into the input modes  and
and  of the beam splitter (see Fig. 1). The two photons then interfere at the beam splitter and are emitted into the output modes
of the beam splitter (see Fig. 1). The two photons then interfere at the beam splitter and are emitted into the output modes  and
and  (see Fig. 1a). Using the dispersive interaction between qubit and resonator, we tune the emission frequencies of the two sources to an identical value of νr = 7.2506 GHz. For our experiments, we sequentially create 20single photons in each source at a rate 1/tr = 1/512 ns∼1.95 MHz in a sequence repeated every 12.5 μs.
(see Fig. 1a). Using the dispersive interaction between qubit and resonator, we tune the emission frequencies of the two sources to an identical value of νr = 7.2506 GHz. For our experiments, we sequentially create 20single photons in each source at a rate 1/tr = 1/512 ns∼1.95 MHz in a sequence repeated every 12.5 μs.
a, False-colour micrograph of the HOM device. A transmon qubit (blue, see inset) controlled by a flux (purple) and charge gate line (orange) through which current or microwave pulses are applied, respectively, is coupled to each coplanar waveguide resonator (green) with fundamental mode  . The coupling rate of the input port of the asymmetric resonator is by a factor of 103 smaller than at the output port. Each resonator output is coupled to the input mode
. The coupling rate of the input port of the asymmetric resonator is by a factor of 103 smaller than at the output port. Each resonator output is coupled to the input mode  (inset) of a microwave beam splitter (dark red) with two output modes
(inset) of a microwave beam splitter (dark red) with two output modes  . b, Schematic of the HOM experiment with two individual cavity quantum electrodynamics systems for photon generation, a beam splitter (BS), linear amplification and heterodyne detection using a pair of mixers
. b, Schematic of the HOM experiment with two individual cavity quantum electrodynamics systems for photon generation, a beam splitter (BS), linear amplification and heterodyne detection using a pair of mixers  pumped by a common local oscillator (LO) for correlation function measurements and full quantum state analysis21.
pumped by a common local oscillator (LO) for correlation function measurements and full quantum state analysis21.
To probe the photon statistics in the beam-splitter output modes  and
and  we use two spatially separated heterodyne detection channels21,22 (see dashed rectangle in Fig. 1b). Each channel consists of a set of semiconductor linear amplifiers, and a microwave frequency mixer for downconversion to 25 MHz, followed by an analog-to-digital converter. After further digital downconversion to d.c. and filtering, we extract the two quadrature amplitudes Xa/b(t) and Pa/b(t) corresponding to the complex envelope of the two time-dependent signals23Sa/b(t) = Xa/b(t)+i Pa/b(t). In contrast to many other HOM experiments in which photons in the beam-splitter outputs are detected by single-photon counters, our measurement of the complex envelope is intrinsically photon-number resolving for averaged measurements and allows us to measure coherences of the electromagnetic field. The complex envelopes Sa/b(t) are used to compute the statistics required to extract all relevant quantum correlations measured here21,23. To analyse the digital data, signal processing and statistical analysis are performed in real-time using field-programmable gate array-based electronics24. The noise added by the detection chain is fully characterized by measuring its statistical properties when the output modes
we use two spatially separated heterodyne detection channels21,22 (see dashed rectangle in Fig. 1b). Each channel consists of a set of semiconductor linear amplifiers, and a microwave frequency mixer for downconversion to 25 MHz, followed by an analog-to-digital converter. After further digital downconversion to d.c. and filtering, we extract the two quadrature amplitudes Xa/b(t) and Pa/b(t) corresponding to the complex envelope of the two time-dependent signals23Sa/b(t) = Xa/b(t)+i Pa/b(t). In contrast to many other HOM experiments in which photons in the beam-splitter outputs are detected by single-photon counters, our measurement of the complex envelope is intrinsically photon-number resolving for averaged measurements and allows us to measure coherences of the electromagnetic field. The complex envelopes Sa/b(t) are used to compute the statistics required to extract all relevant quantum correlations measured here21,23. To analyse the digital data, signal processing and statistical analysis are performed in real-time using field-programmable gate array-based electronics24. The noise added by the detection chain is fully characterized by measuring its statistical properties when the output modes  and
and  of the beam splitter are left in the vacuum state with both sources idle21,23. To verify the single-photon character of each source individually, we have measured their second-order cross-correlation functions Ga b(2)(τ). These exhibit clear antibunching24 (see Fig. 2a,b).
of the beam splitter are left in the vacuum state with both sources idle21,23. To verify the single-photon character of each source individually, we have measured their second-order cross-correlation functions Ga b(2)(τ). These exhibit clear antibunching24 (see Fig. 2a,b).
Cross-correlation Ga b(2)(τ) of individual single-photon sources exhibiting single-photon antibunching, source A in a and B in b. c–e, Ga b(2)(τ) when operating both sources simultaneously with delay times δ τ = 0,50,150 ns exhibiting the HOM effect and its dependence on the temporal photon overlap at the beam splitter. f, Second-order auto-correlation Ga a(2)(τ) of mode  for δ τ = 0 exhibiting two-photon coalescence. See the main text for details and a discussion of the offsets indicated in the upper right corner of each panel. Blue dots are data and red lines are theory.
for δ τ = 0 exhibiting two-photon coalescence. See the main text for details and a discussion of the offsets indicated in the upper right corner of each panel. Blue dots are data and red lines are theory.
To investigate two-photon quantum interference, we simultaneously generate two indistinguishable photons ideally realizing a two-mode entangled state  at the beam-splitter outputs. The measured cross-correlation of the beam-splitter output powers is observed to vanish Ga b(2)(τ)≈0 for all τ between −tr/2 and tr/2 (see coloured region in Fig. 2c). Therefore, we conclude that both microwave-frequency photons coalesce at the beam splitter. This is the HOM effect with microwave photons. In our experiments the spatio-temporal coherence of the single-photon states is governed by resonator decay alone, and shows no significant additional dephasing. This is in stark contrast to many other experiments in which decoherence resulting in random frequency differences between interfering photons causes finite correlations at τ∼0 (refs 6, 11, 13). At τ = n tr (n = ±1,±2,,±10), the peak at integer non-zero multiples of the photon generation period reflects the product of the power in each output
at the beam-splitter outputs. The measured cross-correlation of the beam-splitter output powers is observed to vanish Ga b(2)(τ)≈0 for all τ between −tr/2 and tr/2 (see coloured region in Fig. 2c). Therefore, we conclude that both microwave-frequency photons coalesce at the beam splitter. This is the HOM effect with microwave photons. In our experiments the spatio-temporal coherence of the single-photon states is governed by resonator decay alone, and shows no significant additional dephasing. This is in stark contrast to many other experiments in which decoherence resulting in random frequency differences between interfering photons causes finite correlations at τ∼0 (refs 6, 11, 13). At τ = n tr (n = ±1,±2,,±10), the peak at integer non-zero multiples of the photon generation period reflects the product of the power in each output  , which we have normalizedto one.
, which we have normalizedto one.
All measured second-order correlation functions are normalized by a common scaling factor and a relative gain between the two amplification channels. A remaining small offset subtracted from the reconstructed correlation functions is indicated together with its standard deviation (extracted from multiple measurements) in the upper right corner of each panel in Fig. 2. This offset results from the finite statistical uncertainty of measured first-order correlation terms23 and is expected to vanish in the limit of infinite averaging. The measured second-order correlation functions are in good agreement with analytical calculations25 (solid lines in Fig. 2), taking into account the cavity decay rates κ extracted from independent measurements and a fixed detection bandwidth of 20 MHz chosen to reject experimental noise outside the desired band.
To explore the level of indistinguishability between the two interfering photons we introduce a time delay δ τ on the order of the photon decay time 1/κ∼37 ns. For δ τ = 50 ns the correlation function Ga b(2)(τ) remains close to zero at τ = 0, indicating the coalescence of those photons detected with a vanishingly small time difference6,25,26 (see Fig. 2d). Typically this effect is difficult to observe with detectors of insufficient bandwidth or sources with significant dephasing rates13. The small positive correlations observed at τ∼δ τ are due to the decreased temporal overlap of the single-photon spatio-temporal mode functions at the beam splitter, that is, the increased distinguishability of the two photons. At τ∼n tr we observe broadened, lower amplitude correlations. All features are in agreement with theory25 (solid lines).
For δ τ = 150 ns (and δ τ = 100 ns, not shown) the envelopes of the two single-photon mode functions barely overlap at the beam splitter, resulting in fully distinguishable single photons. At τ = ±δ τ and τ = n tr±δ τ (see Fig. 2e) we observe positive correlations with an amplitude 1/4, which originate from single photons impinging on the beam splitter at different times and at different input arms (compare Fig. 2ab). At τ = n tr the correlations between photons in the same beam-splitter input arm sum up to 1/2, as expected.
To clearly distinguish between single-photon antibunching and two-photon coalescence in time-resolved correlation function measurements, we have also measured the second-order auto-correlation function Ga a(2)(τ) of mode  . When operating only one single-photon source Ga a(2)(0) is expected to vanish. However, in the HOM configuration with δ τ = 0 we find Ga a(2)(0) = Ga a(2)(n tr) = Ga b(2)(n tr) = 1 (see Fig. 2f) as there is a 50% probability of detecting two photons in mode
. When operating only one single-photon source Ga a(2)(0) is expected to vanish. However, in the HOM configuration with δ τ = 0 we find Ga a(2)(0) = Ga a(2)(n tr) = Ga b(2)(n tr) = 1 (see Fig. 2f) as there is a 50% probability of detecting two photons in mode  . All measurements of Ga a(2)(τ) are in good agreement with calculations25, both for δ τ = 0 (solid lines) and for δ τ = 100 ns (not shown). Here, it is interesting to note that a second-order auto-correlation function is rarely directly measured, because of the the lack of sufficiently fast single-photon detectors27. In contrast, using our heterodyne detection scheme we are capable of measuring Ga a(2)(τ) for multi-photon states.
. All measurements of Ga a(2)(τ) are in good agreement with calculations25, both for δ τ = 0 (solid lines) and for δ τ = 100 ns (not shown). Here, it is interesting to note that a second-order auto-correlation function is rarely directly measured, because of the the lack of sufficiently fast single-photon detectors27. In contrast, using our heterodyne detection scheme we are capable of measuring Ga a(2)(τ) for multi-photon states.
To distinguish between an equal mixture of the states |20〉 and |02〉, compatible with the observed correlations, and their coherent superposition  , we fully characterize the two-photon states created in our HOM experiment by quantum state tomography. This allows us to probe the entanglement generated between the coalescing two-photon states in the two output ports of the beam splitter. The created states are also referred to as NOON states. In contrast to the NOON states of propagating photons investigated here, NOON states have also been investigated in superconducting circuits with photons localized in resonators28,29.
, we fully characterize the two-photon states created in our HOM experiment by quantum state tomography. This allows us to probe the entanglement generated between the coalescing two-photon states in the two output ports of the beam splitter. The created states are also referred to as NOON states. In contrast to the NOON states of propagating photons investigated here, NOON states have also been investigated in superconducting circuits with photons localized in resonators28,29.
To perform full quantum state tomography on propagating photons, we record four-dimensional histograms of the measured field quadratures Xa, Pa, Xb and Pb. This is an extension of the scheme discussed in ref. 21 to two spatially separated modes. From these measurements we extract all moments of the two-mode field, that is, expectation values of the form  , with n,m,k,l∈{0,1,2}. The total gain of the detection chain is calibrated by preparing an equal superposition state in only one mode, for which we expect half a photon in mode
, with n,m,k,l∈{0,1,2}. The total gain of the detection chain is calibrated by preparing an equal superposition state in only one mode, for which we expect half a photon in mode  . In the analysis we take a residual thermal steady-state population of 0.03 in modes
. In the analysis we take a residual thermal steady-state population of 0.03 in modes  and
and  into account.
into account.
We observe that the first-order moments and all other odd-order moments are zero because all single-photon Fock states are characterized by a fixed photon number and consequently a fully random phase (see Fig. 3a). As each mode carries exactly one photon on average,  and
and  are close to unity, whereas all other second-order moments vanish. The fourth-order moment
are close to unity, whereas all other second-order moments vanish. The fourth-order moment  is observed to be zero, whereas
is observed to be zero, whereas  and
and  are unity, consistent with the coalescence of the two photons into either output. The above observations are consistent with those based on the correlation function measurements in Fig. 2. Most importantly, the two-mode entanglement is indicated by the moment
are unity, consistent with the coalescence of the two photons into either output. The above observations are consistent with those based on the correlation function measurements in Fig. 2. Most importantly, the two-mode entanglement is indicated by the moment  , which is close to 1, as expected. All measured moments of the two-mode entangled state created in our HOM experiment are in good agreement with the predicted ones (see wire frames in Fig. 3a). Note that moments of order five and higher are all close to zero within their statistical errors.
, which is close to 1, as expected. All measured moments of the two-mode entangled state created in our HOM experiment are in good agreement with the predicted ones (see wire frames in Fig. 3a). Note that moments of order five and higher are all close to zero within their statistical errors.
a, Measured moments  , with n,m,k,l∈{0,1,2} up to fourth order and b, density matrix (real part) in the Fock basis for
, with n,m,k,l∈{0,1,2} up to fourth order and b, density matrix (real part) in the Fock basis for  with fidelity 84%. Coloured bars are extracted from data, error bars indicate the standard deviation and wire frames represent the ideal state. c, Measured moments for
with fidelity 84%. Coloured bars are extracted from data, error bars indicate the standard deviation and wire frames represent the ideal state. c, Measured moments for  with corresponding state fidelity 84%. d, Power detected in the two output modes (
with corresponding state fidelity 84%. d, Power detected in the two output modes ( , blue) and (
, blue) and ( , red) for operating only source B (line) or both sources (dots) creating superposition states with relative phase angle ϕ (see text for details).
, red) for operating only source B (line) or both sources (dots) creating superposition states with relative phase angle ϕ (see text for details).
In addition, we have determined the most likely density matrix ρ characterizing the created two-mode entangled propagating photon state from the measured moments and their respective standard deviation following ref. 21. We have restricted the evaluation of moments to less than three photons per output mode, because we create no more than two single photons with our sources. Note that a related analysis has recently been performed in ref. 30. The real part of ρ is shown in Fig. 3b; all elements of the imaginary part of ρ are smaller than 0.02 (not shown). We extract a fidelity of the NOON-type state of F = 〈ψ|ρ|ψ〉 = 84%and a negativity31  . Inefficiencies arise predominantly from residual thermal populations of qubits and resonators, which we estimate to be approximately 3%, from finite qubit coherence times and the associated imperfect cavity state preparations, as well as slight differences in the linewidth of the two resonators.
. Inefficiencies arise predominantly from residual thermal populations of qubits and resonators, which we estimate to be approximately 3%, from finite qubit coherence times and the associated imperfect cavity state preparations, as well as slight differences in the linewidth of the two resonators.
Finally, to explore the interplay between single- and two-photon interference, we have performed experiments with modes  and
and  prepared in superpositions of 0 and 1photon Fock states, that is,
prepared in superpositions of 0 and 1photon Fock states, that is,  and
and  with variable phase ϕ, ideally creating the state
with variable phase ϕ, ideally creating the state  at the beam-splitter output. With these input states, we have first measured the power in the beam-splitter output modes
at the beam-splitter output. With these input states, we have first measured the power in the beam-splitter output modes  (blue line) and
(blue line) and  (red line) when operating only source B and keeping source A idle (see Fig. 3d). In this case, we observe a power level corresponding to 1/4 of a single photon independent of the phase angle ϕ, as expected for an equal superposition of |0〉 and |1〉 impinging on a balanced beam splitter. Operating both sources A and B, we observe a sinusoidal interference with phase ϕ of the two superposition states in the beam-splitter output power of mode
(red line) when operating only source B and keeping source A idle (see Fig. 3d). In this case, we observe a power level corresponding to 1/4 of a single photon independent of the phase angle ϕ, as expected for an equal superposition of |0〉 and |1〉 impinging on a balanced beam splitter. Operating both sources A and B, we observe a sinusoidal interference with phase ϕ of the two superposition states in the beam-splitter output power of mode  (blue dots) and
(blue dots) and  (red dots), respectively. The sinusoidal oscillation is a result of the interference between one photon in either output port whereas the offset in power of 1/4 is the result of two-photon coalescence.
(red dots), respectively. The sinusoidal oscillation is a result of the interference between one photon in either output port whereas the offset in power of 1/4 is the result of two-photon coalescence.
For the phase angle ϕ≈0 we have also performed full quantum state tomography (see Fig. 3c). As for the two-photon NOON state we observe antibunching, coalescence and entanglement in the moments  ,
,  and
and  , and
, and  , respectively with close to expected amplitudes (wire frames). The interference of the superposition states is revealed not only in the power
, respectively with close to expected amplitudes (wire frames). The interference of the superposition states is revealed not only in the power  and
and  but also in the coherences with an unbalanced number of creation and annihilation operators. The corresponding state has a fidelity of 84% with respect to the ideal one.
but also in the coherences with an unbalanced number of creation and annihilation operators. The corresponding state has a fidelity of 84% with respect to the ideal one.
Our results suggest that multiple on-demand single-photon sources emitting indistinguishable single photons could be used for creating nonlocal entanglement in quantum repeater or quantum communication applications based on microwave photons.
Methods
The photon generation is realized similarly as discussed in ref. 24. Each photon source consists of a transmon-type qubit (Ec/h = 416 (419) MHz) strongly coupled with rate g/2π = 169 (177) MHz to a transmission line resonator (see Fig. 1a). By adjusting the qubit transition frequencies νa to 8.575 (8.970) GHz with a static magnetic flux applied to the superconducting quantum interference device loop of each qubit, both microwave resonators have the same frequency νr = 7.2506 GHz. To create a single photon using one of the sources, we coherently excite the qubit (lifetime T1 = 1.0 (0.9) μs and dephasing time T2* = 0.4 (0.6) μs) into a state α|g〉+β|e〉 using a resonant 20 ns microwave pulse with a Gaussian envelope (σ = 5 ns). Then, we swap the qubit state into the resonator mode  by tuning the qubit transition frequency with a dynamical magnetic flux pulse into resonance with the resonator for half a vacuum-Rabi period. The flux pulse has a rise and fall time of about 1 ns and a total duration of 3 ns≈π/g. This creates the state α|0〉+β|1〉in the resonator, which for β = 1 corresponds to a single-photon Fock state. The photon is then emitted with a Lorentzian spectrum of linewidth κ/2π = 4.1 (4.6) MHz.
by tuning the qubit transition frequency with a dynamical magnetic flux pulse into resonance with the resonator for half a vacuum-Rabi period. The flux pulse has a rise and fall time of about 1 ns and a total duration of 3 ns≈π/g. This creates the state α|0〉+β|1〉in the resonator, which for β = 1 corresponds to a single-photon Fock state. The photon is then emitted with a Lorentzian spectrum of linewidth κ/2π = 4.1 (4.6) MHz.
References
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Duan, L-M. & Monroe, C. Colloquium: Quantum networks with trapped ions. Rev. Mod. Phys. 82, 1209–1224 (2010).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
O’Brien, J. L., Furusawa, A. & Vučković, J. Photonic quantum technologies. Nature Photon. 3, 687–695 (2009).
Legero, T., Wilk, T., Hennrich, M., Rempe, G. & Kuhn, A. Quantum beat of two single photons. Phys. Rev. Lett. 93, 070503 (2004).
Santori, C., Fattal, D., Vučković, J., Solomon, G. S. & Yamamoto, Y. Indistinguishable photons from a single-photon device. Nature 419, 594–597 (2002).
Kiraz, A. et al. Indistinguishable photons from a single molecule. Phys. Rev. Lett. 94, 223602 (2005).
Riedmatten, H. d., Marcikic, I., Tittel, W., Zbinden, H. & Gisin, N. Quantum interference with photon pairs created in spatially separated sources. Phys. Rev. A 67, 022301 (2003).
Kaltenbaek, R., Blauensteiner, B., Zukowski, M., Aspelmeyer, M. & Zeilinger, A. Experimental interference of independent photons. Phys. Rev. Lett. 96, 240502 (2006).
Beugnon, J. et al. Quantum interference between two single photons emitted by independently trapped atoms. Nature 440, 779–782 (2006).
Maunz, P. et al. Quantum interference of photon pairs from two remote trapped atomic ions. Nature Phys. 3, 538–541 (2007).
Flagg, E. B. et al. Interference of single photons from two separate semiconductor quantum dots. Phys. Rev. Lett. 104, 137401 (2010).
Patel, R. B. et al. Two-photon interference of the emission from electrically tunable remote quantum dots. Nature Photon. 4, 632–635 (2010).
Lettow, R. et al. Quantum interference of tunably indistinguishable photons from remote organic molecules. Phys. Rev. Lett. 104, 123605 (2010).
Sanaka, K., Pawlis, A., Ladd, T. D., Lischka, K. & Yamamoto, Y. Indistinguishable photons from independent semiconductor nanostructures. Phys. Rev. Lett. 103, 053601 (2009).
Sipahigil, A. et al. Quantum interference of single photons from remote nitrogen-vacancy centers in diamond. Phys. Rev. Lett. 108, 143601 (2012).
Moehring, D. L. et al. Entanglement of single-atom quantum bits at a distance. Nature 449, 68–71 (2007).
Shadbolt, P. J. et al. Generating, manipulating and measuring entanglement and mixture with a reconfigurable photonic circuit. Nature Photon. 6, 45–49 (2012).
Bocquillon, E. et al. Coherence and indistinguishability of single electrons emitted by independent sources. Science 339, 1054–1057 (2013).
Eichler, C., Bozyigit, D. & Wallraff, A. Characterizing quantum microwave radiation and its entanglement with superconducting qubits using linear detectors. Phys. Rev. A 86, 032106 (2012).
Menzel, E. P. et al. Path entanglement of continuous-variable quantum microwaves. Phys. Rev. Lett. 109, 250502 (2012).
da Silva, M. P., Bozyigit, D., Wallraff, A. & Blais, A. Schemes for the observation of photon correlation functions in circuit QED with linear detectors. Phys. Rev. A 82, 043804 (2010).
Bozyigit, D. et al. Antibunching of microwave-frequency photons observed in correlation measurements using linear detectors. Nature Phys. 7, 154–158 (2011).
Woolley, M. J., Lang, C., Eichler, C., Wallraff, A. & Blais, A. Signatures of Hong–Ou–Mandel interference at microwave frequencies. Preprint at http://arxiv.org/abs/1304.6068 (2013).
Legero, T., Wilk, T., Kuhn, A. & Rempe, G. Time-resolved two-photon quantum interference. Appl. Phys. B 77, 797–802 (2003).
Steudle, G. A. et al. Measuring the quantum nature of light with a single source and a single detector. Phys. Rev. A 86, 053814 (2012).
Wang, H. et al. Deterministic entanglement of photons in two superconducting microwave resonators. Phys. Rev. Lett. 106, 060401 (2011).
Nguyen, F., Zakka-Bajjani, E., Simmonds, R. W. & Aumentado, J. Quantum interference between two single photons of different microwave frequencies. Phys. Rev. Lett. 108, 163602 (2012).
Israel, Y., Afek, I., Rosen, S., Ambar, O. & Silberberg, Y. Experimental tomography of NOON states with large photon numbers. Phys. Rev. A 85, 022115 (2012).
Vidal, G. & Werner, R. F. Computable measure of entanglement. Phys. Rev. A 65, 032314 (2002).
Acknowledgements
This work was supported by the European Research Council (ERC) through a Starting Grant and by ETHZ. L.S. was supported by EU IP SOLID. A.B. and M.J.W. were supported by NSERC, CIFAR and the Alfred P. Sloan Foundation.
Author information
Authors and Affiliations
Contributions
C.L. and C.E. performed the experiments and analysed the data. C.L. developed the FPGA firmware. M.J.W. and A.B. contributed to its theoretical interpretation. C.L., L.S. and J.M.F. designed and fabricated the sample. C.L., C.E. and L.S. contributed to constructing and maintaining the measurement set-up. C.L. and A.W. co-wrote the manuscript and all authors commented on it. A.W. supervised the project. All experiments were carried out at ETH Zurich.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Lang, C., Eichler, C., Steffen, L. et al. Correlations, indistinguishability and entanglement in Hong–Ou–Mandel experiments at microwave frequencies. Nature Phys 9, 345–348 (2013). https://doi.org/10.1038/nphys2612
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2612
This article is cited by
-
Engineering multimode interactions in circuit quantum acoustodynamics
Nature Physics (2024)
-
On-demand directional microwave photon emission using waveguide quantum electrodynamics
Nature Physics (2023)
-
Quantum efficiency, purity and stability of a tunable, narrowband microwave single-photon source
npj Quantum Information (2021)
-
Realizing a deterministic source of multipartite-entangled photonic qubits
Nature Communications (2020)
-
Experimental interference of uncorrelated photons
Scientific Reports (2019)