Abstract
Entanglement is the central yet fleeting phenomenon of quantum physics. Once being considered a peculiar counter-intuitive property of quantum theory1, it has developed into the most central element of quantum technology. Consequently, there have been a number of experimental demonstrations of entanglement between photons2, atoms3, ions4 and solid-state systems such as spins or quantum dots5,6,7, superconducting circuits8,9 and macroscopic diamond10. Here we experimentally demonstrate entanglement between two engineered single solid-state spin quantum bits (qubits) at ambient conditions. Photon emission of defect pairs reveals ground-state spin correlation. Entanglement (fidelity = 0.67±0.04) is proved by quantum state tomography. Moreover, the lifetime of electron spin entanglement is extended to milliseconds by entanglement swapping to nuclear spins. The experiments mark an important step towards a scalable room-temperature quantum device being of potential use in quantum information processing as well as metrology.
Similar content being viewed by others
Main
Engineering entangled quantum states is a decisive step in quantum technology. Although entanglement among weakly interacting systems such as photons has been demonstrated already in the early stages of quantum optics, deterministic generation of entanglement in more complex systems such atoms or ions, not to mention solids, is a relatively recent achievement11. Usually in solid-state systems rapid dephasing ceases any useful degree of quantum correlations. Either decoupling must be used to protect quantum states or careful materials engineering is required to prolong coherence. Most often however, and this is especially important for solid-state systems, one needs to resort to low (milliKelvin) temperatures to achieve sufficiently robust and long-lasting quantum coherence. Spins are sufficiently weakly coupled to their environment to allow for the observation of coherence at room temperatures.
Diamond defect spins are particularly interesting solid-state spin qubit systems. A number of hallmark demonstrations such as single-, two- and three-qubit operations, high-fidelity single-shot readout12, one- and two-qubit algorithms13, and entanglement between nuclear and electron and nuclear spin qubits have been achieved6,14. Different schemes to scale the system to a larger number of entangled electron spins have been proposed15,16,17. A path towards room-temperature entanglement is strong coupling among the ground-state spin magnetic dipole moment of adjacent defects centres. This mutual dipolar interaction scales as distance d−3 and should be larger than the interaction of each electron spin with the residual paramagnetic impurities or nuclear spin moments in the lattice (Fig. 1d). Typical cutoff distances for strong interaction are thus limited by the electron spin dephasing time (milliseconds) to be around 30 nm. Here we demonstrate entanglement between two electron and nuclear spins at a distance of approximately 25 nm. At these distances magnetic dipole coupling is strong enough to attain high-fidelity entanglement while being able to address the spins individually by super-resolution optical microscopy18.
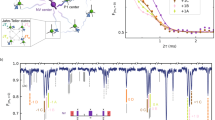
a, Schematics of the NV pair. The two NV centres have different orientations and a distance of  . The magnetic field is aligned with the axis of NV A. b, Level scheme of the combined system of two NV electron spins. Spin transitions with ΔmS = ±1 can be driven with microwaves (straight arrows). Transitions can be addressed individually because different magnetic field alignments result in different Zeeman shifts. c, Optically detected electron spin resonance spectrum of the NV pair at a magnetic field of B = 32 G. Two spin transitions can be attributed to each NV centre. Both show a 15N (I = 1/2) hyperfine structure indicating that they stem from implanted nitrogen. d, Coupling regimes of NV pairs as a function of the limiting coherence time and their separation. The standard strong coupling limit vdip = 1/T(solid line) can be increased to 4vdip = 1/T (dashed) using the enhanced coupling of double quantum coherences. The parameters of the pair used in this work are marked as a red diamond. Inset, optically resolved lateral distance between the two NV centres obtained by microwave-assisted super-resolution microscopy. The measured lateral distance is 21.8±1.7 nm (see Supplementary Information). e, Double electron–electron resonance experiment on the dipolar coupled NV pair. The oscillation shown is a direct measure of the coupling frequency vdip = 4.93±0.05 kHz.
. The magnetic field is aligned with the axis of NV A. b, Level scheme of the combined system of two NV electron spins. Spin transitions with ΔmS = ±1 can be driven with microwaves (straight arrows). Transitions can be addressed individually because different magnetic field alignments result in different Zeeman shifts. c, Optically detected electron spin resonance spectrum of the NV pair at a magnetic field of B = 32 G. Two spin transitions can be attributed to each NV centre. Both show a 15N (I = 1/2) hyperfine structure indicating that they stem from implanted nitrogen. d, Coupling regimes of NV pairs as a function of the limiting coherence time and their separation. The standard strong coupling limit vdip = 1/T(solid line) can be increased to 4vdip = 1/T (dashed) using the enhanced coupling of double quantum coherences. The parameters of the pair used in this work are marked as a red diamond. Inset, optically resolved lateral distance between the two NV centres obtained by microwave-assisted super-resolution microscopy. The measured lateral distance is 21.8±1.7 nm (see Supplementary Information). e, Double electron–electron resonance experiment on the dipolar coupled NV pair. The oscillation shown is a direct measure of the coupling frequency vdip = 4.93±0.05 kHz.
The optical as well as spin physics of nitrogen vacancy (NV) defects in diamond has been subject to numerous investigations11,19. The fluorescence intensity of the strongly allowed optical transition between ground and excited spin triplet states depends on the magnetic quantum number of the ground state and it is larger for mS = 0 and smaller for mS = ±1, allowing optical read-out of the electron spin20. The coherence time T2 of the NV− electron spin depends on the concentration of 13C spins and reaches up to 3 ms for 12C enriched diamond11.
To generate strongly coupled defect pairs with high probability and at the same time optimum decoherence properties, we have implanted nitrogen ions (15N+) with kinetic energies of 1 MeV, corresponding to an implantation depth of 730 nm using a 10-μm-thick mica nano-aperture mask (hole diameter 20 nm). This process creates NV pairs at distances less than 20 nm with a success rate of 2% (see Supplementary Information)21.
Figure 1b shows the spin energy levels of the NV pair together with the optically detected electron spin resonance spectrum of two coupled electron spins. The spectrum in secular approximation is described by

where D is the zero field splitting or fine structure, B is the magnetic field, γe is the gyromagnetic ratio and SA(B) is the spin operator of NV A(B). Electron spin flip-flop terms such as (Sx ASx B,Sy ASy B) can be neglected as long as the energetic detuning between two spins is larger than their dipolar coupling vdip (see Supplementary Information). The two defects are oriented along two different directions of the diamond lattice and hence the orientation dependence of the fine structure term allows for individual addressing by different microwave frequencies. To investigate the magnetic dipolar coupling between the two defects we induce spin transitions (ΔmS = ±1) on both defects and use NV A as a sensitive magnetometer22 to measure spinflip-induced changes of the magnetic dipole field of NV B yielding a dipolar coupling constant of vdip = 4.93±0.05 kHz (Fig. 1e). The effective coupling strength can be enlarged up to four times by exploiting the qutrit nature of the triplet spin in each NV centre. Namely, the quantum phase of a superposition state with ΔmS = ±2 evolves twice as fast in a given magnetic fields as the ΔmS = ±1 superposition. Furthermore, a spinflip by ΔmS = ±2 induces a twice as strong magnetic field change compared with the case of ΔmS = ±1. Hence, using ΔmS = ±2 (double quantum transitions, DQ) on both NVs yields vdip DQ = 19.72±0.2 kHz. It is worth mentioning that these double quantum coherences have half the dephasing time of a single quantum transition under the influence of Markovian magnetic field noise. To create high-fidelity entanglement, strong coupling has to apply (that is, vdip>1/T, where T is the relevant coherence time). The present moderate coupling is masked by spectral diffusion of the two individual electron spins(T2A DQ* = 27.8±0.6 μs and T2B DQ* = 22.6±2.3 μs); that is, vdip<1/T2*. This limitation can be overcome by eliminating low-frequency environmental noise components through further refocusing steps in the entanglement process resulting in a new lower limit for strong coupling vdip>1/T2. The electron spin relaxation and coherence times of the two NVs are T1 = 1.12±0.26 ms, T2A DQ = 150±18 μs and T2B DQ = 514±50 μs. The measured values for dipolar interaction and T2DQ allow a maximum distance of 29.6±1.4 nm between the two defects. The actual distance obtained by involving microwave-assisted super-resolution microscopy yields 25±2 nm. Note that the coupling did not change over months, indicating the room-temperature stability of the defect pair.
After optically initializing the system in |mSA,mSB〉 = |00〉 a double quantum π/2 rotation on both NVs leads to 1/2(|−1−1〉−|1−1〉−|−11〉+|11〉). Under the influence of mutual dipolar coupling the system is evolving freely for a time τ resulting in a state-dependent phase acquisition 1/2(e−iϕ|−1−1〉−|1−1〉−|−11〉+e−iϕ|11〉), where ϕ = 2πvdip DQ and τ is the correlated phase due to dipolar interaction. After a double quantum π rotation and a further free evolution period τ, a second phase is accumulated 1/2(e−i2ϕ|−1−1〉+|1−1〉+|−11〉+e−i2ϕ|11〉). With a final double quantum π/2 rotation the accumulated phase is mapped onto 1/2((e−i2ϕ−1)|−1−1〉+(e−i2ϕ+1)|11〉). For 2τ = 1/2vdip DQ = 25 μs this is  , a maximally entangled Bell state (for details see Supplementary Information). Using local operations this state can be transformed into a set of different entangled states, for example two π pulses transform to ΦDQ+ to
, a maximally entangled Bell state (for details see Supplementary Information). Using local operations this state can be transformed into a set of different entangled states, for example two π pulses transform to ΦDQ+ to  . Figure 2b shows the state evolution on application of the entanglement gate as a function of interaction time τ. The blue line is a simulation of the entangling gate using Hamiltonian (1) with coherence times taken from experimental data. For τ = 12.5 μs the state has evolved to ΦDQ+. As the evolution into ΦDQ+ would not be visible in the fluorescence signal it was transformed into Φ− using local gates. We have performed a density matrix tomography of the final entangled state (for details see Supplementary Information). The fidelity of the reconstructed density matrix with respect to the target state ΦDQ+ is 0.67±0.04, which is below the simulated fidelity of 0.89. (Fidelity is defined as the proximity of two states given by F = tr(ρ σ), where σ is the measured quantum state and ρ is the target state.) The main reason for this discrepancy is due to errors resulting from the finite duration of microwave pulses. In addition, we quantify the entanglement according to ref. 23 by using the von Neumann relative entropy as = minρ∈disentangledtr(σln(σ/ρ))≈0.16 (0 for no entanglement,
. Figure 2b shows the state evolution on application of the entanglement gate as a function of interaction time τ. The blue line is a simulation of the entangling gate using Hamiltonian (1) with coherence times taken from experimental data. For τ = 12.5 μs the state has evolved to ΦDQ+. As the evolution into ΦDQ+ would not be visible in the fluorescence signal it was transformed into Φ− using local gates. We have performed a density matrix tomography of the final entangled state (for details see Supplementary Information). The fidelity of the reconstructed density matrix with respect to the target state ΦDQ+ is 0.67±0.04, which is below the simulated fidelity of 0.89. (Fidelity is defined as the proximity of two states given by F = tr(ρ σ), where σ is the measured quantum state and ρ is the target state.) The main reason for this discrepancy is due to errors resulting from the finite duration of microwave pulses. In addition, we quantify the entanglement according to ref. 23 by using the von Neumann relative entropy as = minρ∈disentangledtr(σln(σ/ρ))≈0.16 (0 for no entanglement,  for a maximal entangled state).
for a maximal entangled state).
a, Quantum circuit diagram of the entanglement scheme. A spin echo sequence on both individual spins reduces the effect of local noise while preserving the spin–spin interaction. The latter realizes a controlled phase gate that finally leads to the Bell state ΦQ D+after an evolution time of 1/8vdip. b, Final state of the entanglement scheme as a function of evolution times τ. The graph includes the simulated fidelity of reaching Φ−. Note that ΦDQ+ was transformed to Φ− at the end of the sequence to allow for a fluorescence contrast. c,d, Real and imaginary part of the density matrix tomography of the  state.
state.
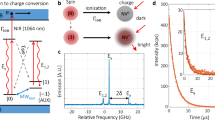
Entanglement between spins is also inferred from fluorescence emission properties of the entangled defect pair. The steady-state fluorescence emission of  ,
,  as well as a correspondingly separable spin state of both NV centres (for example (1/2)(|00〉+|10〉+|01〉+|11〉)) is identical. However, two-photon correlations reveal a difference between spin-entangled and mixed states. A Φ state has a higher probability of simultaneously emitting two photons than an uncorrelated superposition state whereas a Ψ state has a lower probability. In Fig. 3, two-photon correlation measurements and the corresponding classical correlations are shown.
as well as a correspondingly separable spin state of both NV centres (for example (1/2)(|00〉+|10〉+|01〉+|11〉)) is identical. However, two-photon correlations reveal a difference between spin-entangled and mixed states. A Φ state has a higher probability of simultaneously emitting two photons than an uncorrelated superposition state whereas a Ψ state has a lower probability. In Fig. 3, two-photon correlation measurements and the corresponding classical correlations are shown.
a, Results of two-photon correlation measurement for entangled and mixed states. Photons close to the zero delay have been discarded. The inset shows the fitted amplitude of two-photon coincidences at τ = 20 ns. b, Reconstructed population correlation of a  state in a reduced basis of ms = 0 and mS = +1. The fidelity of the main diagonal is F(Φclass−) = 1.07±0.19. c, For
state in a reduced basis of ms = 0 and mS = +1. The fidelity of the main diagonal is F(Φclass−) = 1.07±0.19. c, For  the main diagonal fidelity is F(Ψclass−) = 0.81±0.15 (see Supplementary Information for details). The error bars are given by the fitting error of the photon correlation signal.
the main diagonal fidelity is F(Ψclass−) = 0.81±0.15 (see Supplementary Information for details). The error bars are given by the fitting error of the photon correlation signal.
The lifetime of the entangled states is limited by electron spin dephasing measured to be T2A DQ* = 27.8±0.6 μs and T2B DQ* = 22.6±2.3 μs. The measured entanglement lifetime is T(ΦDQ+) = 28.2±2.2 μs and T(ΨDQ+) = 23.7±1.7 μs (Fig. 4c and Supplementary Information). It is interesting to note that the lifetimes for states Φ+ and Ψ+ are identical although Ψ+ is known to constitute a decoherence-free subspace for dephasing processes that are dominated by magnetic field noise24. However, cancellation of decoherence effects in Ψ+ occurs only if the magnetic field noise is identical for both NV A and NV B (that is non-local). Apparently this is not the case for the pair. One reason is the different orientation of the pair of NVs with respect to B0, which would result in non-ideal decoherence-free subspaces. In addition, from a previous analysis of spin dephasing in diamond defect centres it became clear that electron spin dephasing is dominated by nuclear spins in the nanometre vicinity of the defect.
a, Entanglement storage scheme. Selective π pulses creating a SWAP operation store the entanglement in the nitrogen nuclear spin. b, Fast Fourier transform of the entangled states’ collective phase evolution after entanglement storage (orange) and a reference measurement without entanglement storage (blue). c, The dependence of the entanglement recovery efficiency on the storage time is shown in orange. The solid orange line is the exponential fit to the data whereas the orange dashed line is the simulated storage and retrieval efficiency given the imperfect SWAP gate. Magenta dots and lines are the measurement and fit of T1. The blue and green lines are entanglement lifetimes without storage. The error bars are given by the fitting error of the fast Fourier transform peak.
To store entanglement for a longer period, we designed an experimental scheme (Fig. 4a) to transfer electron spin entanglement to 15N nuclear spins of the NV. Instead of swapping entanglement by driving nuclear spins directly6, we used a combination of a non-aligned static magnetic field previously introduced for state storage25 and selective gates on the electron spins to generate electron nuclear SWAP gates on both NVs. The entanglement swapping protocol used can potentially reach a transfer efficiency of 1; that is, all electron spin entanglement is converted into nuclear spin entanglement (see Supplementary Information). Limited pulse (that is, gate) accuracy however results in an efficiency of around 41% for storage and retrieval in our experiments such that measures based on, for example, the von Neumann relative entropy E indicate nuclear spin entanglement (see Supplementary Information). As shown in Fig. 4c the lifetime of the entangled state with nuclear storage is markedly longer than that of the electron spin state with an effective storage time of over 1 ms. A comparison with the electron spin relaxation time (shown in Fig. 4c) demonstrates that it is the electron T1 that limits the entanglement in the nuclear spin quantum register. We stress that during this time there is no nuclear spin interaction; that is, the timescale on which the nuclear spins are entangled is much faster than their direct coupling (few millihertz) and coupling is slow compared with their decay rate (approximately kilohertz). Decoherence of the stored entangled state could be further suppressed by repolarizing the electron spin (that is, lengthening the effective electron spin T1) allowing nitrogen nuclear coherence times beyond T2* = 7.25 ms (ref. 26). By continuous strong optical excitation of both NV centres further improvement of entanglement storage into the range of seconds seems feasible27.
The experiments presented here mark a first step towards scaling room-temperature diamond quantum registers by demonstrating deterministic entanglement of electron spins over some 10 nm distance. With the advent of diamond defect centre nanotechnology, more efficient generation of defect pairs and larger defect arrays seems to be tractable. For example, decreasing the implantation energy to about 10 keV and using the present mask technology should allow for a pair creation efficiency of almost 100%. Recently, techniques such as nano-implantation with positioning accuracies of 20 nm (ref. 28) and shallow-implanted defects showing dephasing times not degenerated by surface proximity29,30 have improved considerably. With the aid of those techniques, controlled generation of large-scale arrays seems to be within reach, paving the way towards room-temperature quantum devices.
Note added in proof: After submission of the present work a related publication on photon-mediated defect center entanglement was published31.
Methods
NV defects are formed either by nitrogen incorporation during growth or by implantation of nitrogen into high-purity diamond material with a subsequent annealing step. Here we have chosen the latter method to generate proximal diamond defect pairs. The pair was produced by ion implantation in isotope-enriched 12C diamond (99.99%) using a specially designed mica mask with high-aspect-ratio apertures (1:100). Ground-state depletion imaging was performed to identify suitable candidates, which were investigated with double electron–electron resonance. The sample was investigated in a home-built confocal microscope. For coherent control, microwave radiation was synthesized (Rhode-Schwarz SMIQ 03B) and modulated by an IQ (in-phase and quadrature) mixer with an arbitrary waveform generator (Tektronix AWG 520). The microwaves were applied by means of a microstructure forming a split ring resonator lithographically fabricated on the diamond surface.
References
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 0777–0780 (1935).
Aspect, A., Grangier, P. & Roger, G. Experimental realization of Einstein–Podolsky–Rosen–Bohm Gedankenexperiment—A new violation of Bell inequalitites. Phys. Rev. Lett. 49, 91–94 (1982).
Ritter, S. et al. An elementary quantum network of single atoms in optical cavities. Nature 484, 195–200 (2012).
Blatt, R. & Wineland, D. Entangled states of trapped atomic ions. Nature 453, 1008–1015 (2008).
Simmons, S. et al. Entanglement in a solid-state spin ensemble. Nature 470, 69–72 (2011).
Neumann, P. et al. Multipartite entanglement among single spins in diamond. Science 320, 1326–1329 (2008).
Shulman, M. D. et al. Demonstration of entanglement of electrostatically coupled singlet-triplet qubits. Science 336, 202–205 (2012).
Neeley, M. et al. Generation of three-qubit entangled states using superconducting phase qubits. Nature 467, 570–573 (2010).
DiCarlo, L. et al. Preparation and measurement of three-qubit entanglement in a superconducting circuit. Nature 467, 574–578 (2010).
Lee, K. C. et al. Entangling macroscopic diamonds at room temperature. Science 334, 1253–1256 (2011).
Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010).
Neumann, P. et al. Single-shot readout of a single nuclear spin. Science 329, 542–544 (2010).
Shi, F. et al. Room-temperature implementation of the Deutsch-Jozsa algorithm with a single electronic spin in diamond. Phys. Rev. Lett. 105, 040504 (2010).
Pfaff, W. et al. Demonstration of entanglement-by-measurement of solid state qubits. Nature Phys. 9, 29–33 (2012) Advance online publication.
Childress, L., Taylor, J. M., Sorensen, A. S. & Lukin, M. D. Fault-tolerant quantum communication based on solid-state photon emitters. Phys. Rev. Lett. 96, 070504 (2006).
Rabl, P. et al. A quantum spin transducer based on nanoelectromechanical resonator arrays. Nature Phys. 6, 602–608 (2010).
Yao, N. Y. et al. Scalable architecture for a room temperature solid-state quantum information processor. Nature Commun. 3 (2012).
Rittweger, E., Han, K. Y., Irvine, S. E., Eggeling, C. & Hell, S. W. STED microscopy reveals crystal colour centres with nanometric resolution. Nature Photon. 3, 144–147 (2009).
Aharonovich, I., Greentree, A. D. & Prawer, S. Diamond photonics. Nature Photon. 5, 397–405 (2011).
Gruber, A. et al. Scanning confocal optical microscopy and magnetic resonance on single defect centers. Science 276, 2012–2014 (1997).
Pezzagna, S. et al. Creation of colour centres in diamond by collimated ion-implantation through nano-channels in mica. Phys. Status Solidi A 208, 2017–2022 (2011).
Neumann, P. et al. Quantum register based on coupled electron spins in a room-temperature solid. Nature Phys. 6, 249–253 (2010).
Vedral, V., Plenio, M. B., Rippin, M. A. & Knight, P. L. Quantifying entanglement. Phys. Rev. Lett. 78, 2275–2279 (1997).
Ollerenshaw, J. E., Lidar, D. A. & Kay, L. E. Magnetic resonance realization of decoherence-free quantum computation. Phys. Rev. Lett. 91, 217904 (2003).
Childress, L. et al. Coherent dynamics of coupled electron and nuclear spin qubits in diamond. Science 314, 281–285 (2006).
Waldherr, G. et al. High-dynamic-range magnetometry with a single nuclear spin in diamond. Nature Nanotech. 7, 105–108 (2012).
Maurer, P. C. et al. Room-temperature quantum bit memory exceeding one second. Science 336, 1283–1286 (2012).
Toyli, D. M., Weis, C. D., Fuchs, G. D., Schenkel, T. & Awschalom, D. D. Chip-scale nanofabrication of single spins and spin arrays in diamond. Nano Lett. 10, 3168–3172 (2010).
Ohno, K. et al. Engineering shallow spins in diamond with nitrogen delta-doping. Appl. Phys. Lett. 101, 082413 (2012).
Ofori-Okai, B. K. et al. Spin properties of very shallow nitrogen vacancy defects in diamond. Phys. Rev. B 86, 081406(R) (2012).
Bernien, H et al. Heralded entanglement between solid-state qubits separated by 3 meters. Preprint at http://arxiv.org/abs/1212.6136 (2012).
Acknowledgements
The authors would like to acknowledge financial support by the EU through SQUTEC and Diamant, as well as the DFG through SFB/TR21, the research groups 1493 ‘Diamond quantum materials’ and 1482 as well as the Volkswagen Foundation. We thank Y. Wang, R. Kolesov, R. Stöhr, G. Waldherr, S. Steinert, T. Staudacher, J. Michl, C. Burk, E6, J. Biamonte, H. Fedder, F. Reinhard and F. Shi for discussions and support.
Author information
Authors and Affiliations
Contributions
F.D., I.J. and B.N. carried out the experiments. S.P., C.T. and J.M. prepared implantation masks and samples. P.N., F.J. and J.W. supervised experiments. N.Z. analysed experimental data. F.D., P.N., I.J. and J.W. wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 2500 kb)
Rights and permissions
About this article
Cite this article
Dolde, F., Jakobi, I., Naydenov, B. et al. Room-temperature entanglement between single defect spins in diamond. Nature Phys 9, 139–143 (2013). https://doi.org/10.1038/nphys2545
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2545
This article is cited by
-
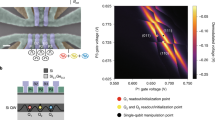
Charge state-dependent symmetry breaking of atomic defects in transition metal dichalcogenides
Nature Communications (2024)
-
Dressed-state control of effective dipolar interaction between strongly-coupled solid-state spins
npj Quantum Information (2023)
-
Method of constructing the entangled state of the particle system
Pramana (2023)
-
Intrinsic decoherence dynamics and dense coding in dipolar spin system
Applied Physics B (2023)
-
Perspective: nanoscale electric sensing and imaging based on quantum sensors
Quantum Frontiers (2023)