Abstract
Attosecond extreme-ultraviolet pulses1 have a complex space–time structure2. However, at present, there is no method to observe this intricate detail; all measurements of the duration of attosecond pulses are, to some extent, spatially averaged1,3,4,5. A technique for determining the full space–time structure would enable a detailed study of the highly nonlinear processes that generate these pulses as a function of intensity without averaging6,7. Here, we introduce and demonstrate an all-optical method to measure the space–time characteristics of an isolated attosecond pulse. Our measurements show that intensity-dependent phase and quantum-path interference both play a key role in determining the pulse structure. In the generating medium, the attosecond pulse is strongly modulated in space and time. Propagation modifies but does not erase this modulation. Quantum-path interference of the single-atom response, previously obscured by spatial and temporal averaging, may enable measuring the laser-field-driven ion dynamics with sub-cycle resolution.
Similar content being viewed by others
Main
Fully defining an attosecond pulse requires knowledge of its phase variation both temporally and spatially. Until now, temporal1,3,4,5,8,9 and spatial10,11,12 measurements are achieved only separately. As the temporal characterization methods (known as RABBIT; ref. 1 and CRAB; refs 3, 4, 5, 9, 13) rely on the photoelectric effect, they average over the spatial profile of a pulse, mixing the contribution from the different emitters of the extreme-ultraviolet (XUV) source at a secondary target. On the other hand, spatial measurements of XUV emission have been achieved using small apertures10,11 or two foci12. Although temporal information remains available in principle, neither method seems compatible with RABBIT or CRAB. Therefore, space–time measurements of attosecond pulses have never been made.
To solve the space–time problem, we turn to an in situ technique. The in situ method is a unique method of measurement that is feasible only for highly nonlinear processes14,15,16. It relies on the fact that adding a single photon to an already highly nonlinear process only weakly perturbs the process17,18. Yet, it can modify the spatial and spectral pattern of a beam. The in situ method has been considered in attosecond pulse metrology to determine only the temporal profile of the average attosecond pulse within attosecond pulse trains14. For that measurement, a weak second-harmonic beam co-propagates with the fundamental beam to break the symmetry between adjacent attosecond pulses, thereby allowing an even-order harmonic signal. Temporal information was encoded in the even-order harmonic signal as a function of the phase delay between the fundamental and second-harmonic laser pulses14.
For our spatially encoded in situ measurement, we produce XUV radiation using the fundamental laser pulse with a time-dependent polarization3 as illustrated in Fig. 1a and described in the Methods. We bring the weak perturbing beam into the medium at a small angle θp to gently modify the process of attosecond pulse generation in space as well as in time. This seemingly small change has a large impact. It perturbs the wavefront of the XUV radiation in the near-field (in the medium), which, in turn, modifies the far-field (at the detector) pattern as illustrated in Fig. 1a. As we delay the perturbing beam relative to the fundamental, we modulate the spatial dependence of the phase and therefore, the near- and far-field patterns. Our perturbing beam serves as a spatial gate. Measuring the far-field pattern as a function of delay τ shown in Fig. 1b allows us to reconstruct the amplitude and phase of the attosecond pulse in space and time in the region where it is produced and, therefore, everywhere in space.
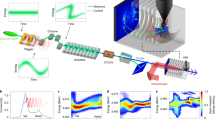
a, An isolated attosecond pulse is generated in a Ne gas jet placed at the focus. The illustrated fundamental laser pulse, E0(t), has a time-dependent polarization to produce an isolated attosecond pulse. We used the second harmonic of the fundamental laser pulse as the perturbation pulse, Ep(t), that crosses the focus at θp = 23 mrad. The perturbation modulates the electron trajectories shown with the blue (red) dotted line for the trajectories with (without) the perturbation. This modulation modifies the XUV wavefront in the near-field, resulting in a change of the propagation angle (θ) and the divergence of the XUV emission. b, The spatially resolved XUV spectra are measured at the far-field. The spectrum is shifted up (τ = 0.5tp) or down (τ = 1.0tp) as the time delay is changed, and tp is the period of the perturbing field (tp = 1.45 fs). See Fig. 2e for the unperturbed XUV spectrum.
Figure 2a,b shows experimental maps constructed from these two-dimensional (2D) images for the energy range of 46±0.8 eV and 79±0.8 eV. In these figure panels, each XUV component is isolated and plotted individually. The vertical axis is the spatial image of the XUV whereas the horizontal axis consists of 48 images placed side-by-side, each taken at a different time delay between the fundamental and the second-harmonic perturbing beam shown on the horizontal axis. Measuring the far-field distribution as a function of delay allows us to determine the amplitude and phase of XUV emission in the near-field.
a,b, Far-field pattern measured as a function of time delay for 46±0.8 eV (a) and 79±0.8 eV (b). c,d, The reconstructed far-field pattern obtained by using the parametric fitting procedure for the range of 46±0.8 eV (c) and 79±0.8 eV (d). The phase difference of the modulations, ΔΦɛ, shown in d is 1.1 rad, which corresponds to a relative emission time of 360 as. e, The spatially resolved XUV spectrum measured at the far-field without the perturbation. f, Reconstructed XUV spectrum in the near-field where the XUV is generated. g, The reconstructed XUV spectrum at the near-field on-axis (red squares) and off-axis (blue circles). The XUV spectra calculated using the SFA on-axis (red solid line) and off-axis (blue solid line).
To analyse the data and reconstruct the pulse, it is convenient to use the strong field approximation (SFA). This is the most intuitive way to treat high-harmonic and attosecond pulse generation19,20. In the SFA, the electron moves along quantum trajectories under the force of the laser field alone. The phase of the XUV emission is determined by the classical action and the XUV emission time. The perturbation to the quantum trajectories induced by the perturbing beam can be derived from the SFA (ref. 17). The phase modification is insensitive to the approximations in the SFA to first order14. In Supplementary Section S1, we arrive at the far-field intensity pattern for the XUV photon energy of ɛ under a 1D approximation as shown in equation (1):

In equation (1), |Eɛfar(θ,τ)|2 is the far-field pattern measured as a function of the propagation angle θ and the time delay τ. kɛ is the wavenumber of the XUV emission, c is the speed of the light and θp is the angle between the fundamental and the perturbation beam. Eɛnear is the complex spectral component of the unperturbed XUV as a function of the vertical position y in the near-field. The superscripts, s and l, are used to denote short and long quantum trajectories. The gate function, Gɛ(y) = , represents the first-order approximation of the amplitude (αɛ) and the phase (σɛ) modification due to the perturbing pulse.
For a given photon energy, the relation between the near- and far-field shown in equation (1) is expressed as a superposition of two 2D spectrograms for short and long trajectories. Reconstructing the spatial structure of an attosecond pulse is equivalent to solving the phase retrieval problem of the unperturbed harmonics (Eɛnear) and the modulation (Gɛ) for both quantum trajectories. If the XUV generation is dominated by a single quantum trajectory, equation (1) becomes a simple spectrogram, and it is the spatial equivalent to the spectrogram used in the frequency-resolved optical gating to reconstruct the spectral amplitude and phase of femtosecond laser pulses21,22,23. One can use the principal component generalized projection algorithm22 for the reconstruction as described in Supplementary Section S2.
To completely reconstruct the XUV radiation generated from both quantum trajectories, we used a parametric fitting procedure as described in Supplementary Section S3. Reconstruction results are shown for 46±0.8 eV and 79±0.8 eV in Fig. 2c,d. The procedure determines the functions Eɛnear(s,l) and Gɛ(s,l) by searching for optimum parameters that produce the observed far-field intensity distribution |Eɛfar(θ,τ)|2. We perform this reconstruction for all energies. Thus, the amplitude and the phase as a function of position at each XUV frequency are directly obtained for both quantum trajectories.
To obtain the temporal information, we recall that the perturbing field imposes a phase modulation14, σɛ(s) = Aɛ(s)sin[kpθp(y−c τ/θp)+Φɛ(s)], on the XUV wavefront with a frequency-dependent amplitude Aɛ(s) and phase Φɛ(s), where kp is the wavenumber of the perturbation. The phase of the modulation, Φɛ(s), depends linearly on the XUV emission time (or group delay)14 that defines the relative spectral phase of the short-trajectory components at the centre of the beam. This connects the spectral and spatial phase. The difference in the phase Φɛ(s) can be directly seen from the modulation as shown in Fig. 2c,d. The phase difference of 1.1 radindicates that the emission times for 46±0.8 eV and 79±0.8 eV radiation differ by 360 as. In this manner, the amplitude and phase of the XUV emission are fully determined for both quantum trajectories in space and time.
Figure 2f clearly shows that the XUV emission is strongly modulated in the near-field (for reference, the unperturbed far-field pattern is shown in Fig. 2e). This modulation occurs because two major quantum paths—short and long trajectories—contribute to the atomic dipole. This quantum-path interference depends on the local intensity, producing the radial dependence of the modulation. In Fig. 2g, we compare the experimental result (data points) with SFA calculations (solid curves). The first destructive interference is observed at 77 eV for the XUV emission generated at the centre of the medium (I0(y = 0) = 3.5×1014 W cm−2). At 7 μm off-centre, we observe that the interference has the opposite phase (I0(y = 7 μm) = 3.2×1014 W cm−2). If all of this radiation is captured by a collection mirror and re-imaged for a streak camera measurement, it is the average of this structure that is measured by RABBIT or CRAB.
Figure 3a,b shows a spatio-temporal snapshot of an isolated attosecond pulse in the nonlinear medium. Figure 3a shows the electric field (colour) of the attosecond pulse as a function of time and position. Figure 3b highlights how the temporal profile changes by moving from the pulse centre (red) to y = 12 μm off-axis (blue). The temporal profile of the attosecond pulse is delayed as we move off-axis. This delay arises because of the intensity-dependent emission time τɛ of the short-trajectory components of the pulse. The emission time contours for the short trajectories at 46 (τ46 eV(s)) and 79 eV (τ79 eV(s)) are shown with dotted lines in Fig. 3a. In contrast, the long-trajectory components (τ79 eV(l)) shows the opposite direction of the delay.
a, The temporal profile of the XUV fields Etnear(y,t) in the near-field is obtained from the reconstructed amplitude and phase. The emission times of the short-trajectory component τ46 eV(s) for 46 eV are shown with squares. The emission times for short- and long-trajectory components τ79 eV(s) and τ79 eV(l) for 79eV are shown with triangles. b, The intensity profiles of the XUV emission in the near-field are shown in red for y = 0 (line-out along red dotted line in a) and blue for y = 12 μm (line-out along blue dotted line in a). Insets: the short-time Fourier transform analysis for the XUV emission for y = 0 (top) and y = 12 μm (bottom). c, The temporal profile of the XUV fields Etfar(θ,t) at the far-field obtained by propagating a. d, The intensity profiles of the XUV emission at the far-field are shown with red for θ = 0 and blue for θ = 2.5 mrad. Insets: the short-time Fourier transform analysis is shown for θ = 0 (top) and θ = 2.5 mrad (bottom). The absolute timing of the attosecond pulse is shifted to get the best fit with the emission times calculated by the saddle point approximation shown with circles in the insets of b.
The emission time of different frequency components of the attosecond pulses can be seen in the time–frequency plots in Fig. 3b, insets. The slope of the emission times measured in the experiment agrees with the slope of the emission times calculated by the saddle point approximation20 shown as circles in Fig. 3b, insets. The slope of the emission time (dτɛ(s)/dɛ), called the atto-chirp, is 8.5 as eV−1 and 11.3 as eV−1 for I0(y = 0) = 3.5×1014 W cm−2 and I0(y = 12 μm) = 2.6×1014 W cm−2, showing the intensity dependence of the atto-chirp (dτɛ/dɛ 1/I0λ; refs 4, 15, 24).
1/I0λ; refs 4, 15, 24).
The XUV pulse observed at the far-field (Fig. 3c) is the coherent superposition of all emissions in the near-field. Time–frequency analysis (Fig. 3d, top inset) shows that the attosecond pulse on-axis in Fig. 3d is mainly composed of lower-energy XUV photons owing to their flat wavefront in the near-field (Supplementary Fig. S3). However, the attosecond pulse at 2.5 mrad off-axis in Fig. 3d is mainly composed of high-energy XUV photons of both the short- and long-trajectory components as shown in Fig. 3d, bottom inset.
All of our measurements have been performed in a thin, low-density jet where limits imposed by the destruction of phase matching are unimportant. However, our approach can be applied more generally. As we reconstruct the XUV radiation from the far-field, the reconstructed XUV radiation in the near-field is the coherent superposition of the radiation in the medium along the propagation direction. For a longer medium, the XUV radiation may vary along the propagation direction. However, the phase matching condition strictly limits the variation of the XUV radiation along the propagation direction. The phase of the XUV radiation cannot slip by more than a half wavelength with respect to the fundamental laser pulse (λXUV(50 eV)/2 = 12 nm) before phase matching is destroyed. In practice, this slip occurs on the fundamental. A similar phase velocity mismatch between the fundamental and second harmonic would have very little influence on our measurement. That means that our in situ measurement can be applied to any condition where phase matching is possible. Although we have concentrated on the case where the jet is at the centre of the focus, our spatially encoded in situ measurement is applicable to other jet positions. In addition, we have assumed a cylindrically symmetric XUV beam because the far-field pattern is sampled by a vertical slit. The reconstruction of asymmetric XUV radiation can also be achieved by measuring the 2D spatial pattern of the XUV beam. For aligned molecules, the XUV radiation may have elliptical polarization25. As the weak perturbing beam mainly affects the propagation of the electron wave packet, the same amount of phase shift will be imposed for orthogonal polarization directions. Therefore, the XUV radiation can be independently reconstructed if the XUV polarization components can be separately measured. Finally, our in situ measurement can be generalized to attosecond pulse trains. For trains, the only modification is that the perturbing beam must have the same wavelength as the fundamental owing to the inversion symmetry of adjacent pulses in the train.
Although we have emphasized space–time characterization of an isolated attosecond pulse, the technique can also be used to measure the time-dependent waveform of the perturbing laser pulse because the deflection angle of the XUV emission is proportional to the field strength of the perturbing beam at the time that the perturbation occurs. Thus, we have constructed an all-optical transient recorder26 that allows us to measure the complete waveform of a laser pulse, including its carrier-envelope phase, with high temporal resolution.
There are three important implications. First, quantum-path interference is prominently revealed in our space–time measurement. This interference is very sensitive to (and therefore will resolve) changes that occur in the ion between the short- and long-trajectory emission times27. It will allow us an unprecedented sub-cycle view of electric-field-driven electronic28 dynamics initiated by tunnelling.
Second, the spatial dimension has never been used for probing attosecond dynamics. Yet, any intensity-dependent phenomenon—such as attosecond hole dynamics7—will be imprinted on the spatial profile of an attosecond or high-harmonic pulse. Our spatially encoded in situ measurement makes the spatial dimension experimentally accessible.
Finally, our results are important for any attosecond pump–probe experiments because space–time coupling limits the temporal resolution that can be achieved. Our all-optical approach characterizes the attosecond pulse in space and time for both quantum trajectories, which can be applied even for weak XUV sources29. The only uncharacterized parameter of an attosecond pulse that remains to be measured is its carrier-envelope phase.
Methods
We used a carrier-envelope-phase-stabilized 5-fs 760-nm Ti:sapphire laser pulse. The stability of the carrier-envelope phase was measured by a single-shot f– 2f interferometer to have a root-mean-square value of 400 mrad. After the second-harmonic generation (200-μm-thick barium borate crystal), the laser beam was divided by a long-wavelength-pass beam splitter. The transmitted beam passed through a 120-μm-thick quartz plate and a broadband quarter-wave plate to create a beam suitable for polarization gating3. The reflected second harmonic was used as a perturbing beam. The two beams were combined, with the perturbing beam parallel but 7 mm below the fundamental, then focused by a 300 mm concave mirror. The angle of the perturbation beam (θp = 23 mrad) was chosen to maximize the deflection angle of the XUV emission without leading to separate diffraction orders17. For a longer medium, the angle of the perturbing beam θp should be chosen to minimize the phase slip between the fundamental and the second-harmonic pulses along the propagation direction (that is, 2k0L(1−cosθp)<π). Here, k0 is the wavenumber of the fundamental and L is the medium length. The time delay between the two pulses was controlled by a piezo stage. Neon gas from a supersonic jet (nozzle diameter of 250 μm with a backing pressure of 4 bar) at the focus served as the nonlinear medium. The laser beam is focused roughly 200 μm below the nozzle with an intensity of I0 = 3.5×1014 W cm−2. The peak intensity of the fundamental beam was estimated from the cutoff energy of the XUV radiation. The off-axis intensity was inferred from the beam profile (40 μm at full-width at half-maximum) measured by a CCD (charge-coupled device) camera. The ratio of intensities between the fundamental (I0) and the perturbing beam (I2ω) was I2ω/I0 = 3×10−4. XUV radiation passed through a ∼250-μm-wide spectrometer slit. The frequency-resolved far-field pattern was recorded with an imaging micro-channel plate and CCD camera. The time–frequency analysis shown in Fig. 3 was made by a short-time Fourier transform with a 200 as Gaussian time window. The details of the reconstruction procedure are explained in the Supplementary Information.
References
Paul, P. M. et al. Observation of a train of attosecond pulses from high harmonic generation. Science 292, 1689–1692 (2001).
Salières, P. et al. Feynman’s path-integral approach for intense-laser-atom interactions. Science 292, 902–905 (2001).
Sansone, G. et al. Isolated single-cycle attosecond pulses. Science 314, 443–446 (2006).
Kim, K. T. et al. Self-compression of attosecond high-order harmonic pulses. Phys. Rev. Lett. 99, 223904 (2007).
Goulielmakis, E. et al. Single-cycle nonlinear optics. Science 320, 1614–1617 (2008).
Zair, A. et al. Quantum path interferences in high-order harmonic generation. Phys. Rev. Lett. 100, 143902 (2008).
Smirnova, O. et al. High harmonic interferometry of multi-electron dynamics in molecules. Nature 460, 972–977 (2009).
Quéré, F., Itatani, J., Yudin, G. L. & Corkum, P. B. Attosecond spectral shearing interferometry. Phys. Rev. Lett. 90, 073902 (2003).
Mairesse, Y. & Quéré, F. Frequency-resolved optical gating for complete reconstruction of attosecond bursts. Phys. Rev. A 71, 011401 (2005).
Lee, D. G., Park, J. J., Sung, J. H. & Nam, C. H. Wave-front phase measurements of high-order harmonic beams by use of point-diffraction interferometry. Opt. Lett. 28, 480–482 (2003).
Frumker, E., Paulus, G. G., Niikura, H., Villeneuve, D. M. & Corkum, P. B. Frequency-resolved high-harmonic wavefront characterization. Opt. Lett. 34, 3026–3028 (2009).
Austin, D. R. et al. Lateral shearing interferometry of high-harmonic wavefronts. Opt. Lett. 36, 1746–1748 (2011).
Chini, M., Gilbertson, S., Khan, S. D. & Chang, Z. Characterizing ultrabroadband attosecond lasers. Opt. Express 18, 13006–13016 (2010).
Dudovich, N. et al. Measuring and controlling the birth of attosecond XUV pulses. Nature Phys. 2, 781–786 (2006).
Doumy, G. et al. Attosecond synchronization of high-order harmonics from midinfrared drivers. Phys. Rev. Lett. 102, 093002 (2009).
Dahlström, J. et al. Atomic and macroscopic measurements of attosecond pulse trains. Phys. Rev. A 80, 033836 (2009).
Bertrand, J. B. et al. Ultrahigh-order wave mixing in noncollinear high harmonic generation. Phys. Rev. Lett. 106, 023001 (2011).
Brugnera, L. et al. Trajectory selection in high harmonic generation by controlling the phase between orthogonal two-color fields. Phys. Rev. Lett. 107, 153902 (2011).
Corkum, P. B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 71, 1994–1997 (1993).
Lewenstein, M., Salières, P. & Ľ’Huillier, A. Phase of the atomic polarization in high-order harmonic generation. Phys. Rev. A 52, 4747–4754 (1995).
Kane, D. J. & Trebino, R. Characterization of arbitrary femtosecond pulses using frequency-resolved optical gating. IEEE Quant. Electron. 29, 571–579 (1993).
Kane, D. J. Recent progress toward real-time measurement of ultrashort laser pulses. IEEE Quant. Electron. 35, 421–431 (1999).
Trebino, R. Measuring the seemingly immeasurable. Nature Photon. 5, 189–192 (2011).
Mairesse, Y. et al. Attosecond synchronization of high-harmonic soft x-rays. Science 302, 1540–1543 (2003).
Smirnova, O. et al. Attosecond circular dichroism spectroscopy of polyatomic molecules. Phys. Rev. Lett. 102, 063601 (2009).
Kienberger, R. et al. Atomic transient recorder. Nature 427, 817–821 (2004).
Zair, A. et al. Molecular internal dynamics studied by quantum path interferences in high order harmonic generation. Preprint at http://arxiv.org/abs/1210.4814v1 (2012).
Goulielmakis, E. et al. Real-time observation of valence electron motion. Nature 466, 739–743 (2010).
Shiner, A. D. et al. Wavelength scaling of high harmonic generation efficiency. Phys. Rev. Lett. 103, 073902 (2009).
Acknowledgements
We gratefully acknowledge the technical assistance of D. Crane and B. Avery. We also acknowledge financial support from NSERC, AFOSR and MURI Grant No. W911NF-07-1-0475. In addition, E.F. acknowledges support from the Marie Curie International Outgoing fellowship.
Author information
Authors and Affiliations
Contributions
K.T.K. and P.B.C. conceived the idea and designed the experiment. K.T.K., C.Z., A.D.S., S.E.K. and G.G. performed the experiment and collected the data. K.T.K. provided the theoretical analysis and analysed the experimental data. K.T.K., D.M.V. and P.B.C. prepared the initial manuscript. All authors contributed in writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 816 kb)
Rights and permissions
About this article
Cite this article
Kim, K., Zhang, C., Shiner, A. et al. Manipulation of quantum paths for space–time characterization of attosecond pulses. Nature Phys 9, 159–163 (2013). https://doi.org/10.1038/nphys2525
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2525
This article is cited by
-
Attosecond field emission
Nature (2023)
-
Attosecond streaking of sub-cycle electron wave packets for probing rescattering dynamics in an intense laser field
Journal of the Korean Physical Society (2023)
-
Spatio-temporal characterization of attosecond pulses from plasma mirrors
Nature Physics (2021)
-
Attosecond streaking using a rescattered electron in an intense laser field
Scientific Reports (2020)
-
Double-blind holography of attosecond pulses
Nature Photonics (2019)