Abstract
For a superconductor, charge and phase are dual quantum variables. A phase-slip event in a superconducting nanowire changes the phase difference over the wire by 2π; it is the dual process to Cooper-pair tunnelling in a Josephson junction. Phase slip by thermal activation at high temperatures is well understood1. Phase slip by quantum tunnelling at low temperatures is considered plausible2,3, but experiments on the resistance of nanowires4,5 are inconclusive on this point. Büchler et al. 6 conclude that successive quantum phase slip (QPS) events can be coherent. Here, we demonstrate that, if it exists, coherent QPS is the exact dual to Josephson tunnelling. A narrow nanowire should act as a QPS junction that shows kinetic capacitance, a plasma resonance and current plateaus of interest for nanoelectronic applications. We suggest feasible experiments to unequivocally confirm the existence for coherent QPS.
Similar content being viewed by others
Main
Phase slip in a thin superconducting wire occurs on the scale of the superconducting coherence length. Phase slip by thermal activation1 is observed as a resistive tail below the critical temperature. In wires with diameter below 10 nm and very high resistance, the energy barrier is small enough that phase slip by quantum tunnelling can be expected2,3. Wires of Mo–Ge deposited on suspended carbon nanotubes have been studied3,4,5, and the results are in reasonable agreement with microscopic calculations of phase-slip rates7,8. All experiments consisted of passing a small d.c. current through the sample and measuring the voltage. As each phase-slip event in the presence of a current I releases an energy I Φ0, where Φ0=h/2e is the flux quantum, with h the Planck constant and e the electron charge, such measurements are dissipative. Unambiguous experimental evidence of QPS is still absent. It has been concluded5 that results can be described by thermally activated phase slip for wires with larger cross-section, and as mesoscopic diffusive normal-metal conductance for the weaker wires. The theoretical analysis is complicated by the fact that the behaviour of the bosonic superfluid may be overshadowed by the fermionic effects of localization and interaction. The superconducting energy gap in the wire may be suppressed and quasiparticles may be generated. However, we are not aware of any reason that would forbid QPS to be a physical reality. We thus assume that coherent QPS may take place, that it is characterized by a transition amplitude ES/2 and that no quasiparticles are present (ES<Δ, Δ being the superconducting energy gap). On the basis of Wentzel–Kramers–Brillouin (WKB)-type estimates3 and microscopic calculations7, we assume that the transition amplitude for QPS in practical superconducting nanowires of 1 μm length can be as high as ES/h=100 GHz.
Wires in which significant QPS occurs have large kinetic inductance L′ and small capacitance C′ per unit length. The plasmon phase velocity cp=(L′C′)1/2 is of order 105 m s−1 (refs 910) and the characteristic impedance Zc=(L′/C′)1/2 is of order 100 kΩ. Frequent QPSs are expected7 when Zc>Rq, with Rq≡h/4e2=6.45 kΩ. A next step in the understanding of QPS was made6 by considering a wire of finite length as a circuit element. If the rest of the circuit is modelled by a parallel resistance Rp, it was predicted that the wire will show a quantum phase transition at Rp=Rq, being superconducting at Rp<Rq and insulating otherwise. As predicted11, a Josephson junction shows qualitatively the same behaviour. The conclusion was then drawn6 that the low-energy physics of QPSs reduces to that of a Josephson junction in the same circuit.
We explicitly demonstrate in this paper that the relation between Josephson tunnelling and QPS in circuits is more intriguing. They are dual to each other with respect to the exchange of the canonically conjugated quantum variables, phase and charge. This duality is exact, in contrast to the widely known12 approximate self-duality of Josephson junction circuits. Results of ref. 6 are reproduced by using exact duality and approximate self-duality. We use exact duality to describe the dynamical response of QPS in the limit of strong phase slip, where we reveal very favourable conditions for the observation of Bloch-type oscillations and of a resonance at the ‘plasma’ frequency.
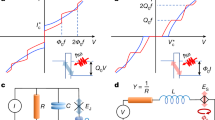
The duality is developed in two steps. We first compare two simple circuits (Fig. 1). One is the Cooper-pair box13 with a Josephson junction that is voltage-biased with voltage V through a capacitor C. In the other we introduce the QPS junction, an element that represents the phase-slip process with strength ES, in a closed loop with an inductor. This is the QPS flux qubit proposed in ref. 14, but not yet realized in practice. In the Cooper-pair box the charging energy depends parabolically on the induced charge ng=C V/2e, for each integer value of the Cooper-pair number n. The charging energy scale is given by EC=(2e)2/2C. Josephson coupling EJ mixes states with n and n+1, lifting degeneracy at half-integer values of ng. The level splitting at this point equals EJ provided EJ≪EC. This is described by the following hamiltonian:

where h.c. represents the hermitian conjugate. In the QPS qubit on the right of Fig. 1 the inductive energy depends parabolically on the applied flux Φ with f=Φ/Φ0 at each integer n that now represents the fluxoid number in the loop. The scale for the inductive energy is EL=Φ02/2L, where L is the inductance of the loop. QPS coupling mixes states with adjacent fluxoid numbers and lifts degeneracy at half-integer values of f. The level splitting at this point equals ES, provided ES≪EL. This implies the following hamiltonian:

The diagram as drawn for the Cooper-pair box is only valid when EC≫EJ, where charge is the relevant quantum number. In analogy, the diagram for the QPS qubit is only valid when EL≫ES, the limit of weak phase slip. Here, phase is the relevant quantum number. The above hamiltonians are obviously equivalent with respect to the exchange

At this stage we have not yet made use of the fact that charge and phase are canonically conjugated quantum variables.
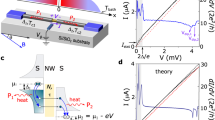
We will now derive the exact duality from this fact. We start by considering a Josephson junction in a linear circuit with either a voltage or a current source (Fig. 2). Any linear circuit can be presented by an equivalent (frequency-dependent) resistor in series with (for voltage bias) or parallel to (for current bias) the junction. A quantum variable describing the circuit is either the phase across the junction or the continuous number of Cooper pairs transferred. Those are canonically conjugated variables so that the corresponding operators of charge ( ) and phase (
) and phase ( ) satisfy
) satisfy  . In the spirit of the Caldeira–Legett approach15, the circuit can be described with the following hamiltonian:
. In the spirit of the Caldeira–Legett approach15, the circuit can be described with the following hamiltonian:

Here,  represents boson-like environment modes, and the coupling term
represents boson-like environment modes, and the coupling term  is different for voltage or current bias,
is different for voltage or current bias,

The operators  and
and  present current and voltage fluctuations, respectively, in the effective resistor and are linear combinations of the environment bosons. The coefficients in these linear combinations are fixed to reproduce the response function of the environment:
present current and voltage fluctuations, respectively, in the effective resistor and are linear combinations of the environment bosons. The coefficients in these linear combinations are fixed to reproduce the response function of the environment:

Here Z(ω) is the frequency-dependent impedance of a serial resistor, Y (ω) the admittance of a parallel resistor and ħ is the reduced Planck constant.
For the hamiltonian of a QPS junction in a circuit, we use the inductive and QPS energies from (1) to obtain

Let us now consider the effect of the canonical transformation  on the hamiltonian (2). Obviously, that transformation does not change the commutation relations. We see that it transforms the QPS hamiltonian into the Josephson hamiltonian with the following parameters:
on the hamiltonian (2). Obviously, that transformation does not change the commutation relations. We see that it transforms the QPS hamiltonian into the Josephson hamiltonian with the following parameters:

Double-sided arrows mean that the transformation exchanges current and voltage bias and series and parallel resistors (Fig. 2). This is the main exact result of our work. These duality relations allow us to exactly map any known result concerning transport characteristics of Josephson junctions in a circuit to dual transport characteristics of QPS junctions in the dual circuit.
The circuits of Fig. 1 were in the regimes EC≫EJ and EL≫ES. Now let us turn to the opposite regimes for the above hamiltonians. For a Josephson junction, this limit is achieved at EJ≫EC, where the phase φ is a well-defined variable. Of particular interest is the dynamics of the classical Josephson junction as described by the resistively shunted junction model

that describes a motion in a slanted sinusoidal (‘washboard’) potential at time t (ref. 1). Time-independent solutions correspond to the zero-voltage state of the junction where the phase is trapped in one of the potential minima. These minima exist provided the drive current I does not exceed the critical current of the junction Ic=2πEJ/Φ0. To obtain the dual counterpart of this equation for the voltage-biased QPS junction we make use of the transformation (3) that relates the circuits (a) and (d) from Fig. 2. The conductor that shunts the Josephson junction is transformed into an external resistor R in series with the QPS junction. Equation (4) becomes an equation for the charge variable q,

where the terms on the right give the voltage drops over QPS junction, inductance and resistor, respectively. This expression is valid in the limit of large phase-slip amplitudes ES≫EL where the charge is a well-defined quantum variable. Here we have a washboard potential in the charge variable. The charge may be trapped in potential minima resulting in an insulating zero-current state provided the bias voltage V does not exceed the critical voltage

For the Josephson junction in the classical regime, the response to small signals follows the kinetic inductance Lkin=Φ0/(2πIccosφ). Similarly for QPS junctions the response is according to a kinetic capacitance

The geometry of Josephson tunnel junctions implies a shunt capacitance. The combination of kinetic inductance and shunt capacitance leads to a resonance at the so-called plasma frequency ωp=(2EJEC)1/2. Because EJ scales with the area and EC scales inversely with it, ωp is independent of area for a homogeneous barrier. For a QPS junction, the natural geometry is a wire with considerable kinetic inductance. Now, the resonance provided by kinetic capacitance (6) and inductance has a frequency

As ES is proportional and EL is inversely proportional to the wire length, the plasma frequency is constant when the length is changed. However, in a lithographically fabricated nanowire it will be easy to lower ωp by adding a wider section of wire that lowers EL without increasing ES (Fig. 3). It is interesting to note that moving from long wires to short wires, the ratio ES/EL decreases in the same way as the decrease of EJ/EC when going from large-area to small-area Josephson junctions. Whereas in the latter case a transition is made from superconducting to insulating response, the wires may be insulating for long lengths and recover superconductivity at shorter lengths.
Top: The junction must be embedded in a highly resistive environment. Parasitic capacitances are sufficiently small for the design given. Left: QPS junction. The parameters correspond to Q=0.5,2πν=ωp,Va.c./Vc=0,1,5 for the thick solid, dashed and thin solid curves respectively. With ES/h=120 GHz and EL/h=30 GHz the plasma frequency is ωp/2π=85 GHz and the critical voltage is Vc=1.56 mV; R=115 kΩ. Right: Voltage Shapiro steps in the dual Josephson circuit with equivalent parameters.
The high-frequency environmental impedance of a submicrometre junction is usually determined by the geometric capacitance and inductance of nearby wiring and, without special precautions, has a value around 300 Ω≪Rq. For a QPS junction this natural impedance leads to a high quality factor of the plasma oscillations given by

Here βL is the equivalent of the well-known McCumber parameter βC for Josephson junctions. Using duality, we predict a strongly nonlinear hysteretic response to relatively small resonant signals Va.c./Vc∼1/QQPS,Va.c. being the amplitude of the applied radiofrequency (RF) signal. The dual effect was investigated for a precision quantum measurement with Josephson junctions16.
The most far-reaching application of QPS junctions might be in a fundamental standard of current, dual to the well-known Josephson voltage standard. Equation (5) can be used to calculate the transport in the series circuit of QPS junction, inductance and resistance. When an RF voltage is applied, the equivalent of Shapiro steps will occur in the form of plateaus at constant current levels

where ν is the RF frequency. For n=1 and ν=80 GHz, as used in Josephson voltage standards, the current level would be 26 nA. High QQPS is unfavourable for this application as it gives rise to a hysteretic current–voltage characteristic, unrealistically high frequencies ∼QQPS and modulation amplitudes ∼QQPS2. To achieve a practical device, the circuit should be made non-hysteretic by the use of a sufficiently high series resistance. As ES/EL cannot be smaller than about 4 to guarantee that charge, as the relevant quantum variable, is well defined, the series resistance has to be at least 60 kΩ. In Fig. 3 we give current–voltage characteristics for a circuit with quality factor Q=0.5, driven at the plasma frequency. Realistic parameters are given in the figure. To fabricate the QPS wire as well as two series resistors of 60 kΩ each, without shunting by parasitic capacitances, is challenging but seems possible with state-of-the-art electron-beam lithography. Many devices could be put in parallel on a chip. The current standard would have to be operated at low temperatures as the presence of quasiparticles leads to a conduction channel parallel to the QPS junction, which would reduce the precision.
The QPS junction at ES≫EL and the Josephson junction at EC≫EJ have in common that the charge is the relevant quantum variable. For Josephson junctions in the charging regime, Bloch oscillations were predicted17,18 and observed19. This system is often considered as dual to the classical Josephson junction, because of the crossover from phase to charge as the quantum variable. However, there is no strict duality as shown for Josephson and QPS. Interestingly, the weak QPS regime with EL≫ES and the classical Josephson junction share the phase as the quantum variable.
References
Tinkham, M. Introduction to Superconductivity 2nd edn 288 (McGraw-Hill, New York, 1996).
Giordano, N. Evidence for macroscopic quantum tunneling in one-dimensional superconductors. Phys. Rev. Lett. 61, 2137–2140 (1988).
Lau, C. N., Markovic, N., Bockrath, M., Bezryadin, A. & Tinkham, M. Quantum phase slips in superconducting nanowires. Phys. Rev. Lett. 87, 217003 (2001).
Bezryadin, A., Lau, C. N. & Tinkham, M. Quantum suppression of superconductivity in ultrathin nanowires. Nature 404, 971–974 (1999).
Bollinger, A. T., Rogachev, A. & Bezryadin, A. Coulomb blockade in the insulating regime of short superconducting nanowires. Preprint at <http://arxiv.org/abs/cond-mat/0508300> (2005).
Büchler, H. P., Geshkenbein, V. B. & Blatter, G. Quantum fluctuations in thin superconducting wires of finite length. Phys. Rev. Lett. 92, 067007 (2004).
Zaikin, A. D., Golubev, D. S., van Otterlo, A. & Zimanyi, G. T. Quantum phase slips and transport in ultrathin superconducting wires. Phys. Rev. Lett. 78, 1552–1555 (1997).
Golubev, D. S. & Zaikin, A. D. Quantum tunneling of the order parameter in superconducting nanowires. Phys. Rev. B 64, 014504 (2001).
Kulik, I. O. Frequency dependence of the penetration depth of an electric field in a superconductor. Fiz. Nizk. Temp. 5, 1391 (1979) English translation: Sov. J. Low Temp. Phys. 5, 656–662 (1979).
Mooij, J. E. & Schön, G. Propagating plasma mode in thin superconducting filaments. Phys. Rev. Lett. 55, 114–117 (1985).
Schmid, A. Diffusion and localization in a dissipative quantum system. Phys. Rev. Lett. 51, 1506–1509 (1983).
Schön, G. & Zaikin, A. D. Quantum coherent effects, phase transitions, and the dissipative dynamics of ultra small tunnel junctions. Phys. Rep. 198, 237–412 (1990).
Bouchiat, V., Vion, D., Joyez, P., Esteve, D. & Devoret, M. H. Quantum coherence with a single Cooper pair. Phys. Scr. T 76, 165–170 (1998).
Mooij, J. E. & Harmans, C. J. P. M. Phase-slip flux qubits. New J. Phys. 7, 219 (2005).
Caldeira, A. O. & Leggett, A. J. Quantum tunnelling in a dissipative system. Ann. Phys. 149, 374–456 (1983).
Siddiqi, I. et al. Direct observation of dynamical bifurcation between two driven oscillation states of a Josephson junction. Phys. Rev. Lett. 94, 027005 (2005).
Averin, D. V., Zorin, A. B. & Likharev, K. K. Bloch oscillations in small Josephson junctions. Sov. Phys. JETP 61, 407–413 (1985).
Likharev, K. K. & Zorin, A. B. Theory of the Bloch-wave oscillations in small Josephson junctions. J. Low Temp. Phys. 59, 347–382 (1985).
Kuzmin, L. & Haviland, D. B. Observation of the Bloch oscillations in an ultrasmall Josephson junction. Phys. Rev. Lett. 67, 2890–2893 (1991).
Acknowledgements
We thank L. Levitov, L. Glazman, T. P. Orlando, C. J. P. M. Harmans, A. D. Zaikin and A. Bezryadin for discussions. Our research is supported by FOM, NanoNed and EuroSQIP.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Mooij, J., Nazarov, Y. Superconducting nanowires as quantum phase-slip junctions. Nature Phys 2, 169–172 (2006). https://doi.org/10.1038/nphys234
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys234