Abstract
Precise understanding of strongly interacting fermions, from electrons in modern materials to nuclear matter, presents a major goal in modern physics. However, the theoretical description of interacting Fermi systems is usually plagued by the intricate quantum statistics at play. Here we present a cross-validation between a new theoretical approach, bold diagrammatic Monte Carlo1,2,3, and precision experiments on ultracold atoms. Specifically, we compute and measure, with unprecedented precision, the normal-state equation of state of the unitary gas, a prototypical example of a strongly correlated fermionic system4,5,6. Excellent agreement demonstrates that a series of Feynman diagrams can be controllably resummed in a non-perturbative regime using bold diagrammatic Monte Carlo.
Similar content being viewed by others
Main
In his seminal 1981 lecture7, Richard Feynman argued that an arbitrary quantum system cannot be efficiently simulated with a classical universal computer, because generally, quantum statistics can only be imitated with a classical theory if probabilities are replaced with negative (or complex) weighting factors. For the majority of many-particle models this indeed leads to the so-called sign problem, which has remained an insurmountable obstacle. According to Feynman, the only way out is to employ computers made out of quantum-mechanical elements7. The recent experimental breakthroughs in cooling, probing and controlling strongly interacting quantum gases prompted a challenging effort to use this new form of quantum matter to realize Feynman’s emulators of fundamental microscopic models7,8. Somewhat ironically, Feynman’s arguments, which led him to the idea of emulators, may be defied by a theoretical method that he himself devised, namely Feynman diagrams. This technique organizes the calculation of a given physical quantity as a series of diagrams representing all the possible ways particles can propagate and interact (for example, ref. 9). For the many-body problem, this diagrammatic expansion is commonly used either in perturbative regimes or within uncontrolled approximations. However, the introduction of diagrammatic Monte Carlo recently allowed one to go well beyond the first few diagrams, and even reach convergence of the series in a moderately correlated regime1,10.
In this Letter we show that for a strongly correlated system and down to a phase transition, the diagrammatic series can still be given a mathematical meaning and leads to controllable results within bold diagrammatic Monte Carlo (BDMC). This approach, proposed in refs 1, 2, 3, is first implemented here for the many-body problem. We focus on the unitary gas, that is, spin-1/2 fermions with zero-range interactions at infinite scattering length4,5,6. This system offers the unique possibility to stringently test our theory against a quantum emulator realized here with trapped ultracold 6Li atoms at a broad Feshbach resonance4,5,6. This experimental validation is indispensable for our theory, based on resummation of a possibly divergent series: although the physical answer is shown to be independent of the applied resummation technique—suggesting that the procedure is adequate—its mathematical validity remains to be proven. In essence, nature provides the ‘proof’. This presents the first—although long-anticipated—compelling example of how ultracold atoms can guide new microscopic theories for strongly interacting quantum matter.
At unitarity, the disappearance of an interaction-imposed length scale leads to scale invariance. This property renders the model relevant for other physical systems such as neutron matter. It also makes the balanced (that is, spin-unpolarized) unitary gas ideally suited for the experimental high-precision determination of the equation of state (EOS) described below. Finally, it implies the absence of a small parameter, making the problem notoriously difficult to solve.
In traditional Monte Carlo approaches, which simulate a finite piece of matter, the sign problem causes an exponential increase of the computing time with system size and inverse temperature. In contrast, BDMC simulates a mathematical answer in the thermodynamic limit. This radically changes the role of the fermionic sign. Diagrammatic contributions are sign-alternating with order, topology and values of internal variables. Because the number of graphs grows factorially with diagram order, a near-cancellation between these contributions is actually necessary for the series to be resummable by techniques requiring a finite radius of convergence. We find that this ‘sign blessing’ indeed takes place.
In essence, BDMC solves the full quantum many-body problem by stochastically summing all the skeleton diagrams for irreducible single-particle self-energy Σ and pair self-energy Π, expressed in terms of bold (that is, fully dressed) single-particle and pair propagators G and Γ which are determined self-consistently (Fig. 1). The density EOS (that is, the relation between total density n, chemical potential μ and temperature T) is given by G at zero distance and imaginary time, n(μ,T)=2 G(r=0,τ=0−). The thermodynamic limit can be taken analytically. The sum of ladder diagrams built on the bare single-particle propagator defines a partially dressed pair propagator Γ0. As Γ0 is well defined for the zero-range continuous-space interaction, the zero-range limit can also be taken analytically. This is in sharp contrast with other numerical methods11,12,13, where taking the thermodynamic and zero-range limits is computationally very expensive. BDMC performs a random walk in the space of irreducible diagrams using local updates. The simulation is run in a self-consistent cycle (along the lines of ref. 2) until convergence is reached. Full details will be presented elsewhere. In essence, our approach upgrades the standard many-body theories based on one lowest-order diagram (for example, refs 14, 15) to millions of graphs.
The skeleton diagrammatic series for the self-energy Σ and the pair self-energy Π is evaluated stochastically (lower box). The diagrams are built on dressed one-body propagators G and pair propagators Γ, which themselves are the solution of the Dyson and Bethe-Salpeter equations (upper box). This cycle is repeated until convergence is reached. G0 is the non-interacting propagator and Γ0 is the partially dressed pair propagator obtained by summing the bare ladder diagrams.
In the quantum degenerate regime, we do not observe convergence of the diagrammatic series for Σ and Π evaluated up to order 9. Here, order N means Σ-diagrams with N vertices (that is, N Γ-lines) and Π-diagrams with N−1 vertices. To extract the infinite-order result, we apply the following Abelian resummation methods16. The contribution of all diagrams of order N is multiplied by , where λn depends on the resummation method: (1) λn=n logn (with λ0=0) for Lindelöf16, (2) λn=(n−1)log(n−1) (with λ0=λ1=0) for ‘shifted Lindelöf’, or (3) λn=n2 for Gaussian17. A full simulation is performed for each ε, and the final result is obtained by extrapolating to ε=0 (Fig. 2).
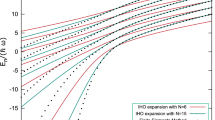
Bold diagrammatic Monte Carlo data for the dimensionless density n λ3, as a function of the parameter ε controlling the resummation procedure, for three different resummation methods: Lindelöf (blue circles), shifted Lindelöf (black diamonds), and Gauss (open green squares). The solid lines are linear fits to the Monte Carlo data, their ε→0 extrapolation agrees within error bars with the experimental data point (filled red square). (In the opposite limit  , the Lindelöf (resp. shifted Lindelöf) curves will asymptote to the first15,21 (resp. third) order results, shown by the dashed (resp. dash–dotted) line.) Error bars for each ε represent the statistical error, together with the estimated systematic error coming from not sampling diagrams of order >9.
, the Lindelöf (resp. shifted Lindelöf) curves will asymptote to the first15,21 (resp. third) order results, shown by the dashed (resp. dash–dotted) line.) Error bars for each ε represent the statistical error, together with the estimated systematic error coming from not sampling diagrams of order >9.
This protocol relies on the following crucial mathematical assumptions: (1) the Nth order contribution of the diagrammatic expansion for Σ (for fixed external variables) is the Nth coefficient of the Taylor series at z=0 of a function g(z) which has a non-zero convergence radius, (2) the analytic continuation g(1), performed by the above resummation methods16,17, is the physically correct value of Σ. The same assumptions should hold for Π.
Proving these assumptions is an open mathematical challenge. Note that Dyson’s collapse argument18 is not applicable to immediately disprove the assumption (1) of a non-zero convergence radius: indeed, unlike QED, our skeleton series is not an expansion in powers of a coupling constant whose sign change would lead to an instability. The first important evidence for the validity of our mathematical assumptions is that the three different resummation methods yield consistent results. For an independent test, we turn to experiments.
The present experiment furnishes high-precision data for the density n as a function of the local value V of the trapping potential (Fig. 3 and Methods). We start the process by obtaining the EOS at high temperatures in the non-degenerate wings of the atom cloud, where the virial expansion is applicable. Once the temperature and the chemical potential have been determined from fits to the wings of the cloud, the data closer to the cloud centre provides a new prediction of the EOS. The process is iterated to access lower temperatures.
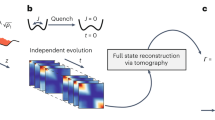
The atom cloud shown contains N=8×104 atoms for each spin state, with a local Fermi energy of EF=370 nK at the centre. a, Absorption image of the atomic cloud after quadrant averaging. b, Reconstructed local density n(ρ,z). c, Equipotential averaging produces a low-noise density profile, n versus V. Thermometry is performed by fitting the experimental data (red) to the known portion of the EOS (solid blue line), starting with the virial expansion for β μ<−1.25 (green dashed line). In this example, the EOS is known for β μ≤−0.25, and the fit to the density profile yields T=113 nK, and β μ=1.63. d, Given μ and T, the density profile can be rescaled to produce the EOS n λ3 versus β μ.
Scale invariance allows one to write the density EOS as n(μ,T)λ3=f(β μ), with  the thermal de Broglie wavelength, β=1/(kBT)the inverse temperature and f a universal function. A convenient normalization of the data is provided by the EOS of a non-interacting Fermi gas, n0λ3=f0(β μ). In Fig. 4a, we thus report the ratio n(μ,T)/n0(μ,T)=f(β μ)/f0(β μ), bringing out the difference between the ideal and the strongly interacting Fermi gas. The Gibbs–Duhem relation allows us to also calculate the pressure at a given chemical potential,
the thermal de Broglie wavelength, β=1/(kBT)the inverse temperature and f a universal function. A convenient normalization of the data is provided by the EOS of a non-interacting Fermi gas, n0λ3=f0(β μ). In Fig. 4a, we thus report the ratio n(μ,T)/n0(μ,T)=f(β μ)/f0(β μ), bringing out the difference between the ideal and the strongly interacting Fermi gas. The Gibbs–Duhem relation allows us to also calculate the pressure at a given chemical potential,  , where
, where  . We normalize it by the pressure of the ideal Fermi gas and show F(β μ)/F0(β μ) (Fig. 4b). The agreement between BDMC and experiment is excellent. The comparison is sufficiently sensitive to validate the procedure of resumming and extrapolating (Fig. 2). The result was checked to be independent of the maximal sampled diagram order Nmax∈{7;8;9} within the error bars shown in Fig. 2 for each ε. The BDMC final error bar in Fig. 4 is the sum of the conservatively estimated systematic errors from the uncertainty of the ε→0 extrapolation and from the dependence on numerical grids and cutoffs, the latter being reduced by analytically treating high-momentum short-time singular parts. The systematic error in the experiment is determined to be about 1% by the independent determination of the EOS of the non-interacting Fermi gas. The experimental error bars of Fig. 4 also include the statistical error, which is <0.5%, thanks to the scale invariance of the balanced unitary gas: irrespective of shot-to-shot fluctuations of atom number and temperature, all experimental profiles contribute to the same scaled EOS-function f. The dominant uncertainty on the experimental EOS stems from the uncertainty in the position of the 6Li Feshbach resonance, known to be at 834.15±1.5 G from spectroscopic measurements19. The change in energy, pressure and density with respect to the interaction strength is controlled by the so-called contact20 that is obtained from Γ in the BDMC calculation. This allows us to define the uncertainty margins above and below the experimental data (Fig. 4) that give the prediction for the unitary EOS if the true Feshbach resonance lies 1.5 G below or above 834.15 G, respectively.
. We normalize it by the pressure of the ideal Fermi gas and show F(β μ)/F0(β μ) (Fig. 4b). The agreement between BDMC and experiment is excellent. The comparison is sufficiently sensitive to validate the procedure of resumming and extrapolating (Fig. 2). The result was checked to be independent of the maximal sampled diagram order Nmax∈{7;8;9} within the error bars shown in Fig. 2 for each ε. The BDMC final error bar in Fig. 4 is the sum of the conservatively estimated systematic errors from the uncertainty of the ε→0 extrapolation and from the dependence on numerical grids and cutoffs, the latter being reduced by analytically treating high-momentum short-time singular parts. The systematic error in the experiment is determined to be about 1% by the independent determination of the EOS of the non-interacting Fermi gas. The experimental error bars of Fig. 4 also include the statistical error, which is <0.5%, thanks to the scale invariance of the balanced unitary gas: irrespective of shot-to-shot fluctuations of atom number and temperature, all experimental profiles contribute to the same scaled EOS-function f. The dominant uncertainty on the experimental EOS stems from the uncertainty in the position of the 6Li Feshbach resonance, known to be at 834.15±1.5 G from spectroscopic measurements19. The change in energy, pressure and density with respect to the interaction strength is controlled by the so-called contact20 that is obtained from Γ in the BDMC calculation. This allows us to define the uncertainty margins above and below the experimental data (Fig. 4) that give the prediction for the unitary EOS if the true Feshbach resonance lies 1.5 G below or above 834.15 G, respectively.
Density n (a) and pressure P (b) of a unitary Fermi gas, normalized by the density n0 and the pressure P0 of a non-interacting Fermi gas, versus the ratio of chemical potential μ to temperature T. Blue filled squares: BDMC (this work), red filled circles: experiment (this work). The BDMC error bars are estimated upper bounds on systematic errors. The error bars are one standard deviation systematic plus statistical errors, with the additional uncertainty from the Feshbach resonance position shown by the upper and lower margins as red solid lines. Black dashed line and red triangles: Theory and experiment (this work) for the ideal Fermi gas, used to assess the experimental systematic error. Green solid line: third order virial expansion. Open squares: first order bold diagram15,21. Green open circles: Auxiliary Field QMC (ref. 11). Star: superfluid transition point from Determinental Diagrammatic Monte Carlo13. Filled diamonds: experimental pressure EOS (ref. 22). Open pentagons: pressure EOS (ref. 23).
Our results clearly differ from previous theoretical and experimental results. Deviations from the theory based on the first-order Feynman diagrams15,21 are expected, and rather remarkably moderate. Differences with lattice Monte Carlo data11,13 may seem more surprising, as in the particular case of the balanced system these algorithms are free of the sign problem, allowing one in principle to approach the balanced unitary gas model in an unbiased way. However, eliminating systematic errors from lattice-discretization and finite volume requires extrapolations which are either not done11 or difficult to control12,13. The ENS experimental pressure EOS (ref. 22) lies systematically below ours, slightly outside the reported error bar. The experimental results from Tokyo23 do not agree with the virial expansion at high temperature. The BDMC results agree well with the present experimental data all the way down to the critical temperature for superfluidity (Fig. 4). On approaching (β μ)c, we observe the growth of the correlation length in the BDMC pair correlation function Γ. A protocol for extracting the critical temperature itself from the BDMC simulation will be presented elsewhere.
We are not aware of any system of strongly correlated fermions in nature where experimental and unbiased theoretical results were compared at the same level of accuracy. Even for bosons, the only analogue is liquid 4He. This promotes the unitary gas to the major testing ground for unbiased theoretical treatments. The present BDMC implementation should remain applicable at finite polarization and/or finite scattering length, opening the way to rich physics which was already addressed by cold atoms experiments6,24,25,26,27. We also plan to extend BDMC to superfluid phases by introducing anomalous propagators. Moreover, as the method is generic, we expect numerous other important applications to long-standing problems across many fields.
Note added in proof: After a preprint of this work became available, new auxiliary-field quantum Monte Carlo data were presented28, with undetermined systematic errors whose evaluation in future work is called for by the authors of ref. 28.
Methods
The experimental set-up has been described previously24. In short, ultracold fermionic 6Li is brought to degeneracy by sympathetic cooling with 23Na. A two-state mixture of the two lowest hyperfine states of 6Li is further cooled in a hybrid magnetic and optical trap at the broad Feshbach resonance at 834 G. We employ high-resolution in situ absorption imaging to obtain the column density of the gas, that is converted into the full 3D density using the inverse Abel transform29. Equidensity lines provide equipotential lines that are precisely calibrated using the known axial, harmonic potential (axial frequency νz=22.83±0.05 Hz). Equipotential averaging yields low-noise profiles of density n versus potential V. Density is absolutely calibrated by imaging a highly degenerate, highly imbalanced Fermi mixture, and fitting the majority density profile to the ideal Fermi gas EOS (ref. 24). In contrast to previous studies22,23, our analysis does not rely on the assumption of harmonic trapping.
Thermometry is performed by fitting the density profile to the EOS constructed thus far, restricting the fit to the portion of the density profile where the EOS is valid. In the high-temperature regime, the EOS is given by the virial expansion

where the virial coefficients are  (ref. 30), and b3=−0.29095295 (ref. 31). Fitting a high-temperature cloud to the virial expansion gives the temperature T and the chemical potential μ of the cloud, and the EOS n λ3=f(β μ) can be constructed. We have used equation (1) for β μ<(β μ)m a x=−1.25 and we checked that our EOS did not change within statistical noise if we instead used (β μ)max=−0.85. Once a new patch of EOS has been produced, it can then in turn be used to fit colder clouds. Iteration of this method allows us to construct the EOS to arbitrarily low temperature. A total of ∼ 1,000 profiles were used, with 10–100 profiles (50 on average) contributing at any given β μ.
(ref. 30), and b3=−0.29095295 (ref. 31). Fitting a high-temperature cloud to the virial expansion gives the temperature T and the chemical potential μ of the cloud, and the EOS n λ3=f(β μ) can be constructed. We have used equation (1) for β μ<(β μ)m a x=−1.25 and we checked that our EOS did not change within statistical noise if we instead used (β μ)max=−0.85. Once a new patch of EOS has been produced, it can then in turn be used to fit colder clouds. Iteration of this method allows us to construct the EOS to arbitrarily low temperature. A total of ∼ 1,000 profiles were used, with 10–100 profiles (50 on average) contributing at any given β μ.
References
Van Houcke, K., Kozik, E., Prokof’ev, N. & Svistunov, B. in Computer Simulation Studies in Condensed Matter Physics XXI (eds Landau, D. P., Lewis, S. P. & Schuttler, H. B.) (Springer, 2008).
Prokof’ev, N. & Svistunov, B. Bold diagrammatic Monte Carlo technique: When the sign problem is welcome. Phys. Rev. Lett. 99, 250201 (2007).
Prokof’ev, N. V. & Svistunov, B. V. Bold diagrammatic Monte Carlo: A generic sign-problem tolerant technique for polaron models and possibly interacting many-body problems. Phys. Rev. B 77, 125101 (2008).
Inguscio M., Ketterle, W. & Salomon, C. (eds) Proc. Int. School of Physics Enrico Fermi, Course CLXIV, Varenna, 20–30 June 2006 (IOS Press, 2008).
Giorgini, S., Pitaevskii, L. P. & Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 80, 1215–1274 (2008).
Zwerger, W. (ed.) in BCS–BEC Crossover and the Unitary Fermi Gas (Lecture Notes in Physics, Springer, 2012).
Feynman, R. Simulating physics with computers. Int. J. Theoret. Phys. 21, 467–488 (1982).
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008).
Fetter, A. & Walecka, J. Quantum Theory of Many-Particle Systems (McGraw-Hill, 1971).
Kozik, E. et al. Diagrammatic Monte Carlo for correlated fermions. Europhys. Lett. 90, 10004 (2010).
Bulgac, A., Drut, J. E. & Magierski, P. Spin 1/2 fermions in the unitary regime at finite temperature. Phys. Rev. Lett. 96, 090404 (2006).
Burovski, E., Prokof’ev, N., Svistunov, B. & Troyer, M. Critical temperature and thermodynamics of attractive fermions at unitarity. Phys. Rev. Lett. 96, 160402 (2006).
Goulko, O. & Wingate, M. Thermodynamics of balanced and slightly spin-imbalanced Fermi gases at unitarity. Phys. Rev. A 82, 053621 (2010).
Strinati, G. C. in BCS–BEC Crossover and the Unitary Fermi Gas (ed. Zwerger, W.) (Lecture Notes in Physics, Springer, 2012).
Haussmann, R. Properties of a Fermi liquid at the superfluid transition in the crossover region between BCS superconductivity and Bose–Einstein condensation. Phys. Rev. B 49, 12975–12983 (1994).
Hardy, G. Divergent Series (Oxford Univ. Press, 1949).
Fruchard, A. Prolongement analytique et systèmes dynamiques discrets. Collect. Math. 43, 71–82 (1992).
Dyson, F. J. Divergence of perturbation theory in quantum electrodynamics. Phys. Rev. 85, 631–632 (1952).
Bartenstein, M. et al. Precise determination of 6Li cold collision parameters by radio-frequency spectroscopy on weakly bound molecules. Phys. Rev. Lett. 94, 103201 (2004).
Braaten, E. in BCS–BEC Crossover and the Unitary Fermi Gas (ed. Zwerger, W.) (Lecture Notes in Physics, Springer, 2012).
Haussmann, R., Rantner, W., Cerrito, S. & Zwerger, W. Thermodynamics of the BCS–BEC crossover. Phys. Rev. A 75, 023610 (2007).
Nascimbène, S., Navon, N., Jiang, K. J., Chevy, F. & Salomon, C. Exploring the thermodynamics of a universal Fermi gas. Nature 463, 1057–1060 (2010).
Horikoshi, M., Nakajima, S., Ueda, M. & Mukaiyama, T. Measurement of universal thermodynamic functions for a unitary Fermi gas. Science 327, 442–445 (2010).
Ketterle, W. & Zwierlein, M. Making, probing and understanding ultracold Fermi gases. Rivista del Nuovo Cimento 31, 247–422 (2008).
Shin, Y., Schunck, C., Schirotzek, A. & Ketterle, W. Phase diagram of a two-component Fermi gas with resonant interactions. Nature 451, 689–693 (2007).
Shin, Y. Determination of the equation of state of a polarized Fermi gas at unitarity. Phys. Rev. A 77, 041603(R) (2008).
Navon, N., Nascimbène, S., Chevy, F. & Salomon, C. The equation of state of a low-temperature Fermi gas with tunable interactions. Science 328, 729–732 (2010).
Drut, J. E., Lähde, T. A., Wlazłowski, G. & Magierski, P. The equation of state of the unitary Fermi gas: An update on lattice calculations. Preprint at http://arxiv.org/abs/1111.5079v1 (2011).
Shin, Y., Zwierlein, M., Schunck, C., Schirotzek, A. & Ketterle, W. Observation of phase separation in a strongly interacting imbalanced Fermi gas. Phys. Rev. Lett. 97, 030401 (2006).
Ho, T-L. & Mueller, E. J. High temperature expansion applied to fermions near Feshbach resonance. Phys. Rev. Lett. 92, 160404 (2004).
Liu, X-J., Hu, H. & Drummond, P. D. Virial expansion for a strongly correlated Fermi gas. Phys. Rev. Lett. 102, 160401 (2009).
Acknowledgements
We thank R. Haussmann for providing propagator data from refs 15, 21 for comparison, and the authors of refs 11, 13, 22, 23 for sending us their data. This collaboration was supported by a grant from the Army Research Office with funding from the Defense Advanced Research Projects Agency (DARPA) Optical Lattice Emulator program. Theorists acknowledge the financial support of the Research Foundation Flanders (FWO) (K.V.H.), National Science Foundation (NSF) grant PHY-1005543 (University of Massachusetts group), Swiss National Science Foundation (SNF) Fellowship for Advanced Researchers (E.K.), and l’Institut Francilien de Recherche sur les Atomes Froids (IFRAF) (F.W.). Simulations ran on the clusters CM at UMass and Brutus at ETH. The MIT work was supported by the NSF, AFOSR-MURI, ARO-MURI, Office of Naval Research (ONR), DARPA Young Faculty Award, an AFOSR Presidential Early Career Award for Scientists and Engineers (PECASE), the David and Lucile Packard Foundation, and the Alfred P. Sloan Foundation.
Author information
Authors and Affiliations
Contributions
K.V.H. (theory) and M.J.H.K. (experiment) contributed equally to this work. K.V.H., F.W., E.K., N.P. and B.S. developed the BDMC approach for unitary fermions; the computer code was written by K.V.H. assisted by F.W.; simulation data were produced by F.W., E.K. and K.V.H.; M.J.H.K., A.T.S., L.W.C., A.S. and M.W.Z. all contributed to the experimental work and the analysis. All authors participated in the manuscript preparation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Van Houcke, K., Werner, F., Kozik, E. et al. Feynman diagrams versus Fermi-gas Feynman emulator. Nature Phys 8, 366–370 (2012). https://doi.org/10.1038/nphys2273
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2273
This article is cited by
-
Accelerated quantum Monte Carlo with probabilistic computers
Communications Physics (2023)
-
Transition from a polaronic condensate to a degenerate Fermi gas of heteronuclear molecules
Nature Physics (2023)
-
Single-particle excitations in the uniform electron gas by diagrammatic Monte Carlo
Scientific Reports (2022)
-
Cold atoms stay cool
Nature Physics (2021)
-
A combined variational and diagrammatic quantum Monte Carlo approach to the many-electron problem
Nature Communications (2019)