Main

Spontaneous Raman and Brillouin scattering are common to almost any media. Incident photons are annihilated in these processes, giving rise to scattered photons at redder Stokes or bluer anti-Stokes frequencies. These scattering events lead to the creation or annihilation of phonons, respectively. Although previous research in optomechanics has used bolometric forces9,10,11, centrifugal radiation pressure12,13,14,15,16,17,18 and optical gradient force19,20,21 to excite mechanical motion of device boundaries, it is only recently that electrostrictive Brillouin scattering 5,6,7 was demonstrated in microcavities. As electrostriction is one aspect of radiation pressure, extensive work in radiation pressure cooling13,14,15,16,17,18 raises the question of whether it is possible to cool phonon modes by means of a Brillouin process, similar to the scattering process available in bulk media1. For achieving Brillouin anti-Stokes cooling, the heating Stokes line needs to be eliminated. However, as low acoustic frequencies separate the pump line from the Stokes and anti-Stokes lines, filtering out the Stokes line against the anti-Stokes line requires a rapid transmission change over an extremely small frequency difference, which is not easily available in bulk materials. Here we transform the energy flow direction in spontaneous Brillouin scattering using two discrete optical resonances separated by the mechanical-resonance frequency. This allows the Brillouin cooling process to gain efficiency and selectivity by pumping at the lower resonance and emitting anti-Stokes photons at the upper resonance. This is different from systems with a single optical resonance, where cooling was achieved by detuning the pump below the resonance by a distance equal to the frequency of the mechanical mode22. Furthermore, in contrast to boundary-deforming optomechanical systems10,12,13,14,15,16,17,18 where the radial vibration can leak through the support, the whispering-gallery mechanical mode7 here propagates azimuthally along the device equator. This orthogonal relationship reduces anchoring-related dissipation, and thus the mechanical quality factor here can approach the material limit1.

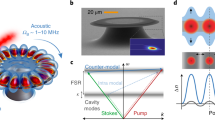
Our room-temperature and atmospheric-pressure experiment (Fig. 1c) is based on a silica microsphere resonator 23 of Qoptical>108. We evanescently couple light into the resonator by means of a tapered optical fibre24. Light is coupled out from the other side of this taper, allowing interrogation of the acoustical mode by means of the light that is scattered from it. This spherical resonator supports the three participants in the Brillouin cooling process—two optical resonances (pump and anti-Stokes) and one acoustical resonance. The acoustical and the optical modes are of a whispering-gallery type and circulate in unison with considerable overlap. These three modes are coupled by means of photoelastic scattering induced by density change (Supplementary Equations (S9)–(S11)), and the electrostrictive effect (Fig. 1a and Supplementary Equation (S24)), that are two facets of one single mutual coupling defined by the electrostrictive constant, γe, of the material. Experimental interrogation of the acoustical mode is made possible through observations of the pump light that it scatters (and Doppler shifts) into the anti-Stokes mode. The beat note between the pump light and the anti-Stokes light is measured on a photodetector at the output of the taper and is a measurement of the acoustical mode. The mechanical deformation of the sphere is illustrated with 12 acoustical wavelengths along the circumference in Fig. 1c. This illustration corresponds to an experimentally observed (Figs 2–4) acoustical mode of frequency Ωa=95 MHz on a 77.5-μm-radius sphere, which we numerically calculate in the Supplementary Information. In this work, we will experimentally cool this mechanical mode.

Figure 1: Conceptual description of Brillouin cooling.
figure 1

a, Cooling of an acoustic wave through the interplay between anti-Stokes photoelastic scattering and electrostrictive pressure. b, Selectively enabling Brillouin anti-Stokes cooling (a) while rejecting Stokes heating is achieved by relying on a resonator with asymmetric optical resonance structure (right) that matches the energy and momentum of the acoustical mode being cooled (left). c, Pump photons photoelastically scatter from the Brownian acoustical mode, and thermal energy is removed because only the anti-Stokes process is resonantly enhanced. Inset: finite-element method (FEM) calculation of an acoustical mode with 12 wavelengths around the circumference, which corresponds to the frequency Ωa=95 MHz on a 77.5-μm-radius sphere. The amplitude and index perturbation are calculated for 300 K.

Full size image
Figure 2: Experimental observation of cooling and heating of a 95 MHz acoustical mode in the microsphere system.
figure 2

The spectra of power reflectance from the density-wave fluctuation are provided as a function of input optical power. The fact that the area under the Lorentzian curves becomes smaller at high input power while the linewidth broadens indicates that cooling is occurring. To cool the acoustical mode (left), we pump the low-frequency optical resonance (OP) to only resonantly enhance the anti-Stokes process while suppressing the Stokes process. For the heating experiment (right), we pump the higher-frequency optical resonance (OaS) instead, to resonantly enhance the Stokes process. The noise floor drops at high optical power because the measurement is performed with more pump light inside the cavity for which a normalization is carried out.

Full size image

Although energy considerations give a general explanation for cooling, an explicit solution is needed. We therefore also analytically derive the cooling process while starting from the acoustical- and optical-wave equations in the Supplementary Information. The source terms in these equations are taken to be electrostrictive pressure for the acoustical wave, and photoelastic index change for the optical wave. As expected from energy considerations, the solution shows that light applies compressive pressure on the region of the acoustical wave that expands, to take away energy from sound. We also confirm that repeating the same calculation for the Stokes process gives pressure on the acoustical regions while they shrink so that energy is imparted to the acoustical wave as expected. The classical analysis also shows that higher acoustical and optical quality factors, and lower acoustical frequencies, improve the cooling ratio (Supplementary Equation (S44)). A quantum analysis25 provides more details on the feasibility of this system towards ground-state cooling17,18,26, and is used to estimate the optomechanical coupling strength g0 in Supplementary Section S5. The principal enablers for Brillouin cooling are: the selective resonant enhancement of the anti-Stokes cooling process over the Stokes process; and phase matching for the two optical modes and the acoustic mode interacting through the Brillouin process (Methods and Fig. 1b).

Experimental measurement of Brillouin cooling is shown in Fig. 2, left, as indicated by the broadening of the beating signal between the pump and anti-Stokes lines, as a function of increasing pump power. This beat observed from the tapered fibre coupler serves as a measurement of the acoustical mode (see Supplementary Information). The cooling experiment is carried out by positioning the pump laser at the lower-frequency resonance (ωP in Fig. 1b), and by observing the light scattered in the anti-Stokes direction into the ωaS resonance. As in refs 10, 13, we prefer linewidth as a measurement of cooling10,13,14,15,16,17,18,26,27,28 because the alternative of measuring the integrated power of the beat note might be affected by attenuation of the optical signals. As the power reflectance spectrum is proportional to the squared displacement spectrum of the acoustical mode (see Supplementary Information), the acoustical linewidth has been extracted from this data and is presented in Fig. 3a. Here, the linewidth of the 95 MHz acoustical mode increases from 7.7 kHz to 118 kHz with increasing pump power, in an open laboratory environment at 294 K. We measure the effective mode temperature through its inverse proportionality to the linewidth of the acoustical mode (see Supplementary Information). The result indicates an achieved cooling ratio of 15, implying an effective mode temperature of 19 K at the maximum observed cooling point. The cavity operates in the thermally stable regime29. The cooling factor we achieved was limited by the optical power available from the pump laser. To complete the analysis, we now invert this process by moving the pump to the higher-frequency resonance. The low-frequency optical mode now functions as a Stokes resonance for the higher-frequency pump. As expected, line narrowing is now observed as indicated in Fig. 3a, accompanied by growth of the Stokes signal (Fig. 2, right). The Stokes process linewidth and the anti-Stokes cooling linewidth converge at low input powers, indicating the mechanical quality factor of the mode. This point of convergence provides the 7.7 kHz acoustical linewidth calibration at 294 K in Fig. 3, so that mode temperature can be calculated during the cooling experiment. On the basis of the frequency-Q product reported for silica1, one can calculate a material-limited mechanical Q to be 7 times higher than what we measured here. We believe that transitioning to vacuum, where air dissipation plays no role, will allow getting closer to the material-limited Q.

Figure 3: Experimental measurement of acoustical mode temperature.
figure 3

a, We capture linewidth data from a cooling and heating experiment, and calculate the effective acoustical mode temperatures. As expected, both cooling and heating linewidths converge towards the Brownian room-temperature linewidth at low optical pump power. The green dash–dot line is a fit to the theory in Supplementary Equation (S44). Error bars indicate the 95% confidence bounds for the measured linewidth. b, We calibrate the acoustical linewidth as a function of temperature by finding the point of convergence of the cooling and heating data. The narrowest observed cooling linewidth (top) and the widest observed heating linewidth (bottom) are averaged to estimate the 7.7 kHz linewidth for the acoustical mode at ambient temperature of 294 K. FWHM, full-width at half-maximum.

Full size image

We experimentally confirm that two optical resonances exist that are separated by the mechanical frequency, as required for phase-matched cooling. We already know that the pump to anti-Stokes beat, measured by a photodetector, provides us with a frequency of 95 MHz for the mechanical mode (Fig. 4a, right). We then carry out the following two independent measurements that obtain no information from this electrical measurement. Measuring resonator transmission while scanning the pump frequency (Fig. 4b) indeed confirms the existence of two optical resonances spaced by 95 MHz to within measurement error. We also verify that the relevant resonance structure is indeed asymmetric relative to the pump by confirming that no resonance appears on the Stokes side of pump resonance OP at a spacing of 95 MHz. The optical line frequency spacing is also measured by repeating the Stokes experiment7 but now with an optical spectrum analyser at the output. As expected, the spectrum analyser resolves two optical lines that are separated by 95 MHz (Fig. 4a, left) in agreement with the measured transmission profile. These three independent measurements—beat spectrum, optical transmission and the optical output spectrum—confirm the existence of the resonant triplet that was used in the cooling process.

Figure 4: Experimental verification of phase matched optical and acoustical modes.
figure 4

a, The participating resonances are analysed by three independent experimental measurements, confirming that the optical signals beating on the photodetector (right) indeed originate from one pump and one Stokes optical line as resolved with an optical spectrum analyser (left). b, The separation between these optical lines corresponds with the transmission spectrum of our device, measured by sweeping the pump wavelength. Absorption peaks that overlap the lines resolved in a (left) are seen. Resonances are named according to their role in the cooling experiments.

Full size image

Here we use forward Brillouin scattering3,7 in a system involving two optical modes and one acoustical mode to demonstrate cooling. In comparison, previous optical cooling studies have used fluorescence30, radiation pressure forces13,14,15,16,17,18 and photothermal pressure10. Although the end result here combines a net annihilation of phonons10,13,14,15,16,17,18,26,30 in a multi-resonance system5,6,7,8, no detuning of the pump with respect to the resonance is required for achieving cooling. Furthermore, the fact that the mechanical mode is of a whispering-gallery type here, indicates low dissipation through the support7. Although we selected the 95 MHz mode in this study because of the greater cooling ratio achievable for such relatively low frequencies (Supplementary Equation (S44)), mechanical modes spanning from tens of megahertz7 to tens of gigahertz5,6 can be accessed with this method. In a broad context, Brillouin scattering belongs to a family of scattering processes that includes Raman and Rayleigh scattering. Reversing the energy flow direction here, with respect to Brillouin systems such as those used in refs 3, 5, 6, 7, raises the question of whether similar inversion is possible with Raman scattering31 non-optomechanical cooling of solids30,32,33 in spite of the higher frequencies involved.

Methods

Phase matching and selective resonant enhancement of the anti-Stokes process.

Selective resonant enhancement of the anti-Stokes process (Fig. 1a) is made possible owing to the non-periodic frequency separation34,35 of the high-order optical resonances of the sphere. Here we exploit this non-periodic resonance structure for solely selecting the anti-Stokes line. The phase-matching requirement implies that the anti-Stokes photon should carry out the energy (ω) and momentum (M) of the pump photon and the thermal phonon. In a spherical resonator, the momentum parameter Mrelates to azimuthal propagation ei(Mφ−ωt) around the sphere equator. As expected, these conservation considerations36 are in agreement with our analytically derived synchronous solution for the coupled-wave equations1 that describe our system (see Supplementary Information). Both phase matching and selective resonant enhancement are illustrated in the energy–momentum (ω−M) diagram of Fig. 1b. As the pump optical resonance (ωP, MP) and the anti-Stokes resonance (ωaS, MaS) are separated by the acoustical resonance parameters (Ωa, Ma), as indicated by the filled triangles, both phase matching and resonant enhancement are satisfied for anti-Stokes scattering. On the other hand, the dashed triangle of Fig. 1b illustrates the off-resonantly eliminated Stokes process, where subtraction of the same acoustical parameters (Ωa, Ma) from the pump resonance (ωP, MP) brings us to a region (ωS, MS) where no optical resonances exist.