Abstract
An intense laser pulse in a plasma can accelerate electrons1,2,3,4 to GeV energies in centimetres5,6,7. Transverse betatron motion8,9 in the plasma wake results in X-ray photons with an energy that depends on the electron energy, oscillation amplitude and frequency of the betatron motion10,11,12. Betatron X-rays from laser-accelerator electrons have hitherto been limited to spectra peaking between 1 and 10 keV (ref. 13). Here we show that the betatron amplitude is resonantly enhanced when electrons interact with the rear of the laser pulse14,15. At high electron energy, resonance occurs when the laser frequency is a harmonic of the betatron frequency, leading to a significant increase in the photon energy. 108 gamma-ray photons, with spectra peaking between 20 and 150 keV, and a peak brilliance >1023 photons s−1 mrad−2 mm−2 per 0.1% bandwidth, are measured for 700 MeV beams, with 107 photons emitted between 1 and 7 MeV. Femtosecond duration gamma-rays may find uses in imaging, isotope production, probing dense matter, homeland security and nuclear physics16.
Similar content being viewed by others
Main
X-ray pulses from synchrotron sources have become immensely useful tools for investigating the structure of matter17, which has led to a huge international effort to construct light sources for many different scientific and technological applications. Synchrotrons are usually based on radio-frequency (RF) accelerating cavities that are limited to fields of 10–100 MV m−1 because of electrical breakdown, which results in very large and expensive devices.
High-power lasers, on the other hand, have led to the development of many new areas of science, as diverse as inertial confinement fusion and laboratory astrophysics to the study of warm dense matter. However, they now have the potential to transform accelerator and light source technology. In the late 1970s, Tajima and Dawson1 proposed harnessing the ponderomotive force associated with intense laser fields to excite plasma waves and form wake-like structures18 (as behind a boat) that travel with a velocity close to the speed of light, c. The electrostatic forces of these charge density structures can rapidly accelerate particles to very high energies6; where momentum is gained analogous to a surfer riding an ocean wave. Recent progress in the development of laser wakefield accelerators (LWFAs) has enabled electron beams to be accelerated with unprecedented acceleration gradients2,3,4, three orders of magnitude higher than in RF cavities, thus reducing a 100 m long GeV accelerator to centimetres in length6. The LWFA can now produce high-quality electron beams with low emittance, ɛn, of the order 1πmm mrad19, small energy spread20, δ γ/γ≪1%, where γ is the Lorenz factor, and high charge4, Q=10–100 pC. At high laser intensities, in the so-called blowout regime21, the LWFA structure has an approximately spherical bubble shape with a radius of  , which is primarily determined by the normalized laser vector potential, a0=e A/mec2and the plasma frequency,
, which is primarily determined by the normalized laser vector potential, a0=e A/mec2and the plasma frequency,  , where np is the plasma density, e, the electron charge and me, the electron mass22. The plasma wave is efficiently driven when the laser pulse duration is approximately a plasma period. Micrometre-long electron bunches that extend only a fraction of the plasma wavelength, λp=2π c/ωp, are self-injected and accelerated5,22, which leads to peak currents of kiloamperes3. This makes the LWFA an attractive candidate for driving compact synchrotron and free-electron laser16 radiation sources. As a first step towards developing a compact source, synchrotron emission from an undulator driven by a LWFA has been demonstrated23. However, the confining force of the bubble structure can also act as an effective wiggler to produce X-ray radiation peaking in the sub-ångström range10.
, where np is the plasma density, e, the electron charge and me, the electron mass22. The plasma wave is efficiently driven when the laser pulse duration is approximately a plasma period. Micrometre-long electron bunches that extend only a fraction of the plasma wavelength, λp=2π c/ωp, are self-injected and accelerated5,22, which leads to peak currents of kiloamperes3. This makes the LWFA an attractive candidate for driving compact synchrotron and free-electron laser16 radiation sources. As a first step towards developing a compact source, synchrotron emission from an undulator driven by a LWFA has been demonstrated23. However, the confining force of the bubble structure can also act as an effective wiggler to produce X-ray radiation peaking in the sub-ångström range10.
The electrostatic fields inside the plasma bubble21 give rise to very large forces. For a laser spot equal to the plasma bubble diameter, the laser energy is depleted over a length Lp d=γg2c τl, where γg=ω0/ωp is the relativistic factor associated with the laser group velocity22. Typically, when a0≥3, electrons are injected into the bubble from the background plasma2,3,4 and accelerate until they reach the dephasing length22,  . At the dephasing point the energy gained is γd≈2γg2a0/3. The restoring force of the bubble results in harmonic oscillations of electrons in the bubble at a characteristic betatron frequency,
. At the dephasing point the energy gained is γd≈2γg2a0/3. The restoring force of the bubble results in harmonic oscillations of electrons in the bubble at a characteristic betatron frequency,  . The conjugate variables of the oscillator are the excursion and momentum, with respective amplitudes rβ and mec aβ, where
. The conjugate variables of the oscillator are the excursion and momentum, with respective amplitudes rβ and mec aβ, where  is the normalized transverse momentum, with γ the Lorentz factor, kp=2π/λp, and
is the normalized transverse momentum, with γ the Lorentz factor, kp=2π/λp, and  the normalized transverse velocity. As in a conventional wiggler, radiation is emitted within a half-angle φ=aβ/γ, as a series of harmonics
the normalized transverse velocity. As in a conventional wiggler, radiation is emitted within a half-angle φ=aβ/γ, as a series of harmonics  , where
, where  is the average longitudinal Lorentz factor and his the harmonic number. When aβ≥1, the longitudinal Lorentz factor is modulated at even harmonics of ωβ and the spectrum contains many merged harmonics with a critical harmonic at hc≈3aβ3/8, giving
is the average longitudinal Lorentz factor and his the harmonic number. When aβ≥1, the longitudinal Lorentz factor is modulated at even harmonics of ωβ and the spectrum contains many merged harmonics with a critical harmonic at hc≈3aβ3/8, giving  , which is close to the synchrotron critical energy, Ec≈3ℏωp2rβγ2/2c (ref. 24). The radiation rate, determined from the Lienard–Wiechert potentials24, scales with γ2, and Nphot=(2π/9)αfaβ photons per electron are emitted every betatron oscillation cycle, where αf=1/137 is the fine structure constant. To obtain a high photon flux and high photon energies the energy and betatron amplitude should be maximized for a given ωp.
, which is close to the synchrotron critical energy, Ec≈3ℏωp2rβγ2/2c (ref. 24). The radiation rate, determined from the Lienard–Wiechert potentials24, scales with γ2, and Nphot=(2π/9)αfaβ photons per electron are emitted every betatron oscillation cycle, where αf=1/137 is the fine structure constant. To obtain a high photon flux and high photon energies the energy and betatron amplitude should be maximized for a given ωp.
The presence of the laser field inside the bubble can drastically change the electron dynamics25. When the laser partially fills the bubble (τl≥R/c) it can interact with the electrons. As the average velocity of oscillating electrons increases, owing to acceleration by the longitudinal force of the bubble, they see a continually evolving Doppler-downshifted frequency of the laser radiation. The electrons oscillate anharmonically because of the nonlinear relationship between velocity and momentum. This allows them to be resonantly driven at harmonics of the betatron frequency. For linearly polarized laser radiation, this interaction can be described by the driven nonlinear oscillator equation  , where Γ=ɣ̇/γ is the damping rate due to the relativistic mass increase and FL y=e(dA/dt−ẏ∂ A/∂ y) is the Lorentz force. The γ-dependence of ωβ leads to a shift of the resonance on a slow timescale, and anharmonic motion on a fast timescale. The laser frequency can be shifted by several per cent to ω′0 by photon deceleration26 and is Doppler-shifted to
, where Γ=ɣ̇/γ is the damping rate due to the relativistic mass increase and FL y=e(dA/dt−ẏ∂ A/∂ y) is the Lorentz force. The γ-dependence of ωβ leads to a shift of the resonance on a slow timescale, and anharmonic motion on a fast timescale. The laser frequency can be shifted by several per cent to ω′0 by photon deceleration26 and is Doppler-shifted to  , where γ′g is the Lorentz factor for the group velocity of the segment of the laser pulse interacting with the electrons in the bubble. The oscillation amplitude grows rapidly when Γ≪ωβ and the laser frequency is in resonance with a harmonic of the betatron frequency,
, where γ′g is the Lorentz factor for the group velocity of the segment of the laser pulse interacting with the electrons in the bubble. The oscillation amplitude grows rapidly when Γ≪ωβ and the laser frequency is in resonance with a harmonic of the betatron frequency,  , where l is the harmonic number. Γ vanishes at dephasing (z≃Ld), when ɣ̇→0, causing the betatron amplitude to increase suddenly. At this point both aβ and γ are at their maximum. Harmonically resonant betatron motion is clearly observed in numerical simulations using the OSIRIS particle in cell (PIC) code27, for our experimental parameters, as shown in Fig. 1a. Electrons that are injected at the rear of the ‘bubble’ initially perform independent betatron oscillations arising from their initial transverse position and momentum (Fig. 1b). The amplitude of these ‘free’ oscillations are relativistically damped owing to the longitudinal acceleration (that is, Γ>0). When resonance occurs (that is, Γ≈0 and phase ≃π) the betatron amplitude grows rapidly until rβ≈R, as shown in Fig. 1g. As the laser phase is the same for all the electrons at a given longitudinal position, these forced oscillations have identical phase and the trajectories coalesce14, as shown in the well-defined oscillations evident in Fig. 1c,d. The increase in the transverse momentum aβ causes the Doppler-shifted laser frequency to drift into resonance with harmonics of ωβ (as observed in Fig. 1h). Electrons can be driven at harmonics of the betatron frequency because of anharmonic motion arising from the nonlinear velocity–momentum relationship. They eventually begin to decelerate and leave the plasma at an arbitrary phase of the high-amplitude oscillation, with only a residual phase space spread, that is the emittance is conserved from the original ‘free’ oscillation and is similar to that just after injection, whereas the high-amplitude oscillation of the transverse momentum leads to shot-to-shot pointing variations.
, where l is the harmonic number. Γ vanishes at dephasing (z≃Ld), when ɣ̇→0, causing the betatron amplitude to increase suddenly. At this point both aβ and γ are at their maximum. Harmonically resonant betatron motion is clearly observed in numerical simulations using the OSIRIS particle in cell (PIC) code27, for our experimental parameters, as shown in Fig. 1a. Electrons that are injected at the rear of the ‘bubble’ initially perform independent betatron oscillations arising from their initial transverse position and momentum (Fig. 1b). The amplitude of these ‘free’ oscillations are relativistically damped owing to the longitudinal acceleration (that is, Γ>0). When resonance occurs (that is, Γ≈0 and phase ≃π) the betatron amplitude grows rapidly until rβ≈R, as shown in Fig. 1g. As the laser phase is the same for all the electrons at a given longitudinal position, these forced oscillations have identical phase and the trajectories coalesce14, as shown in the well-defined oscillations evident in Fig. 1c,d. The increase in the transverse momentum aβ causes the Doppler-shifted laser frequency to drift into resonance with harmonics of ωβ (as observed in Fig. 1h). Electrons can be driven at harmonics of the betatron frequency because of anharmonic motion arising from the nonlinear velocity–momentum relationship. They eventually begin to decelerate and leave the plasma at an arbitrary phase of the high-amplitude oscillation, with only a residual phase space spread, that is the emittance is conserved from the original ‘free’ oscillation and is similar to that just after injection, whereas the high-amplitude oscillation of the transverse momentum leads to shot-to-shot pointing variations.
a, Snapshot of the electron distribution. b–d, Electron beam trajectories for the strongly damped (b), weakly resonant (c) and strongly resonant (d) case. e–h, The evolutions, for a selected trajectory, are shown of γ (e), aβ, (f), rβ (g), and the first (black line), second (green line) and third harmonics (blue line) of ωβ, and  , the Doppler-shifted laser frequency as seen by the electrons (red line) (h). The three vertical dashed lines indicate the different regimes that can occur with almost the same γ: strongly damped case (I), weakly resonant case (II), strongly resonant case (III). Parameters used in simulation: ne=1.8×1018 cm−3λ=800 nm, laser spot size 35μm, laser pulse duration 70 fs and initially a0=3. The normalized transverse momentum varies from aβ=5.6 for rβ=1 μm to aβ=150 for rβ=20 μm, at γ=1,600. The laser field, with frequency ω0′ and phase velocity vp, acts on electrons co-moving with longitudinal velocity vz, at the downshifted frequency
, the Doppler-shifted laser frequency as seen by the electrons (red line) (h). The three vertical dashed lines indicate the different regimes that can occur with almost the same γ: strongly damped case (I), weakly resonant case (II), strongly resonant case (III). Parameters used in simulation: ne=1.8×1018 cm−3λ=800 nm, laser spot size 35μm, laser pulse duration 70 fs and initially a0=3. The normalized transverse momentum varies from aβ=5.6 for rβ=1 μm to aβ=150 for rβ=20 μm, at γ=1,600. The laser field, with frequency ω0′ and phase velocity vp, acts on electrons co-moving with longitudinal velocity vz, at the downshifted frequency  . Efficient energy transfer from laser to betatron motion requires resonance (that is,
. Efficient energy transfer from laser to betatron motion requires resonance (that is,  , where l is the betatron harmonic number).
, where l is the betatron harmonic number).
In a realistic experiment, electron injection is a highly nonlinear process that depends on both the laser and plasma properties5,22,26. As a result the injection point and the net acceleration length can vary. Thus, for a fixed plasma medium length, the wakefield acceleration structure can vanish either before dephasing (I—illustratedin Fig. 1), at dephasing (II) or beyond dephasing (III). Close to dephasing, rβ and aβ can grow substantially without an appreciable change in γ, as can be seen in Fig. 1. This accounts for the variability of the electron beam properties of the LWFA.
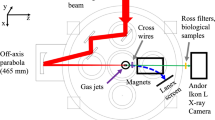
To investigate the potential of betatron emission as a brilliant source of gamma-rays, we have focussed a 5 J, 55±5 fs duration laser pulse from the ASTRA-Gemini laser28 into a preformed plasma waveguide16,29 with np≈2×1018 cm−3, as shown in Fig. 2. The initial vector potential a0≃2 is enhanced as a result of the nonlinear evolution of the laser fields and can easily treble in value, which leads to self-injection and quasi-monoenergetic electron bunches.
A F/16 spherical mirror focuses the laser pulse (5 J, 55±5 fs, 800 nm) to a 40±5 μm diameter spot at the entrance of the 4 cm long, 300 μm diameter, pre-formed plasma capillary waveguide29 with an on-axis density of np≈1.8–2.0×1018 cm−3. The laser beam initially has an intensity of 9×1018 W cm−2, which corresponds to a0=2 and a bubble radius R=10 μm. A 600 μm thick Al foil blocks laser light from X-ray detectors. Lanex 1 and Image Plate 1 are used to measure the high-energy portion of the electron spectra simultaneously with the X-ray beam profiles (dipole field set to 0.7 T) or the electron beam profile alone (dipole field set to zero). Image Plate 2, placed on axis, records the X-ray profile, phase contrast images and, with cut-off filters, the spectra. The CdTe detector, placed in a screened enclosure, records Compton side-scattered radiation. For further details see the Methods section.
Resonant betatron emission has been investigated by simultaneously monitoring the electron beam properties using an electron energy spectrometer, LANEX (ref. 30) screens and image plates31, and X-ray photon properties, using image plates and/or a semiconductor X-ray detector. During the investigation, three distinct sets of data (corresponding to regions I, II and III in Fig. 1) have been recorded. In all cases the electron energy was around 700 MeV. In the first experiment, carried out at a density of ≈1.6×1018 cm−3 (obtained with 50 mbar gas pressure in the capillary waveguide), we studied the highly damped (Γ≫0) stage (I) by determining the photon energy peak and angular divergence. By increasing the density to ≈2×1018 cm−3 (obtained with 60 mbar gas pressure in the capillary waveguide) the dephasing length is reduced, thus allowing the weakly and strongly resonant regimes (II and III, where Γ≈0) to be investigated.
X-rays emitted in the highly damped stage (I) have spectra centred around 20 keV, which precluded the use of the CdTe detector32 because of strong Kα emission at 30 keV from the semiconductor bulk. As an alternative, a set of copper and tungsten cut-off filters has been used to selectively attenuate the X-ray flux and estimate the spectral content, which is then correlated with the electron spectra. The spectra peak around 20 keV, which corresponds to a critical photon energy of 50–60 keV, and the X-ray beam has an angular divergence ≈14 mrad, as shown in Fig. 3. This is consistent with ne≃1.6×1018 cm−3, rβ≃3 μm and aβ≈20.
a, X-ray image as transmitted through calibrated metallic cut-off filters (0.3 mm (top left) and 1 mm (bottom left) tungsten foils, 0.5 mm (top right) and 1 mm (bottom right) copper foils). The calibrated cut-off filters give a spectral peak at 20 keV (Ec≈60±15 keV). b, X-ray beam profile used to deduce a divergence of 14 mrad, measured simultaneously with the 700 MeV electron beam shown in c.
Increasing the plasma density by 20% reduces the dephasing length and allows the undamped resonant regime (II and III) to be entered. X-ray spectra, shown in Fig. 4, have been recorded using a CdTe pixellated semiconductor detector, which is described in the Methods Section. The X-ray spectrum in Fig. 4a peaks at 50 keV (Ec≈150 keV), which corresponds to the weakly resonant case (II), where injection occurs later and the electron bunch exits the potential before dephasing and growth in rβ has taken place. In contrast, the peak at 150 keV (Ec≈450 keV), shown in Fig. 4b, corresponds to a strongly resonant interaction with the laser (III) and evolution that has already passed dephasing. This compares well with analytical calculations and numerical simulations using the OSIRIS PIC code27, which give rβ=20 μm, aβ=150, ne=2×1018 cm−3 and γ=1,600, shown in Fig. 1. Electrons radiate very high energy photons at the dephasing point and are then decelerated again. In both cases (II and III) the average electron energy was 630±70 MeV.
To prove that the gamma-rays originated from a source with a size equal to the betatron amplitude we have projected phase-contrast shadow images of fine wires onto an X-ray image plate, as shown in Fig. 5. By comparing the measured images from five different thickness wires, from 20 to 100 μm in diameter, with those predicted for different source sizes we have found that a 15 μm source produces consistent phase contrast images for all wires. This source size corresponds to a betatron amplitude rβ of 7.5 μm, which is in good agreement with that predicted by OSIRIS for the weakly resonant case (II) and gives a value of aβ=50.
a, Phase contrast image recorded on an image plate, showing images of four copper wires of 100, 75, 50 and 40 μm thickness, respectively from left to right. b, Lineout shows profiles where the faint shadow of a fifth 25 μm thick wire is just visible at position 3 mm. c–f, Plots of the shadows cast by the wires (squares) compared with simulated data (solid lines) that are consistent with a 15 μm diameter X-ray source size. Simulations assume a X-ray spectrum ranging from 10 to 100 keV. The error bars are calculated from the standard deviation of the signal variation from pixel to pixel.
The betatron motion of very energetic electrons results in an intense narrow beam of X-rays, which will be polarized predominantly in the plane of betatron motion. The X-ray pulse length is estimated to be ≈10 fs from simulations, shown in Fig. 1d, which is a reasonable assumption because the greatest number of high-energy photons are emitted when aβ is large at resonance. From the X-ray detection efficiency we have estimated the number of emitted photons to be about 5×108. By determining the source size from phase contrast images of thin wires, a peak brilliance of 1023 photons s−1 mrad−2 mm−2 per 0.1% bandwidth has been estimated. The regime of operation can be chosen by varying the plasma density and channel length. In the strongly resonant regime for γ>2,000 it should be possible to produce a large flux of photons in the MeV range. This would also require higher laser intensities and a lower plasma density, for example a0=10, ne=1018 cm−3 and γ=5,500, rβ=R=34 μm gives aβ≈340, which will produce photons with a critical energy >5 MeV with an efficiency of the order of 1% per betatron cycle. Such a source of polarized gamma-ray photons would open up new applications in high-contrast imaging of weakly absorbing and hot dense matter, time-resolved probing of the nucleus, the production of medical radio-isotopes through photo-nuclear reactions and the production of polarized elementary particles.
Methods
Two different X-ray detectors have been used in the experiments. Single-shot X-ray spectra have been measured using a single-photon multi-pixel CdTe detector32, originally developed at CERN. The detector has been calibrated using laboratory sources and its response to X-ray radiation over a wide energy range modelled and reproduced using GEANT4 (ref. 33). As the detector was not suitable for directly measuring the entire photon spectrum, ranging from 10 keV to more than a MeV, especially towards the higher end, it was necessary to use an indirect method to determine the spectrum. The X-ray spectra, in the weakly and strongly resonant regimes, have been measured in a single shot using the semiconductor detector to detect 90° Compton side-scattered betatron radiation from a 12 mm diameter aluminium rod. Compton scattering downshifts the X-ray spectrum such that spectra in the MeV range can be detected with adequate resolution using only the 1 mm thick semiconductor detector, which has a range from 20 keV to 600 keV. Moreover, the flux of the incoming radiation is reduced without requiring filters or attenuators. GEANT4 was used to estimate the properties of the synchrotron-like spectra of the X-rays striking the aluminium rod.
Phase-contrast images of fine copper wires have been recorded on X-ray image plates (FUJI-BAS-MS-2325), which consist of a layer of barium fluorohalide phosphor crystals embedded in a plastic supporting medium. When these are exposed to X-rays, secondary electrons that are produced in the interaction are trapped in lattice defects. These then emit blue light when illuminated by 640 nm light34 on readout in the scanning system. The image plate is sensitive mainly to photons in the 4–80 keV (ref. 35) range but can also detect higher energies photons with reduced sensitivity. They are widely used for X-ray imaging thanks to their excellent dynamic range, efficiency and large area35.
Simulations were carried out using the PIC code OSIRIS (ref. 27). We performed 2D PIC simulations for an incident laser pulse with a tranverse and longitudinal Gaussian shaped envelope a0(r,t)=exp[−r2/σr2−t2/t2]. The laser pulse parameters used in the simulations were σ(FWHM)=35 μm, τ(FWHM)=70 fs and a peak a0=3. The background plasma density used for the simulations was np=1.8×1018 cm−3 with a linear ramp up of 100 μm, followed by a constant density over 2 cm, and then a symmetric ramp down of 100 μm. The grid size used in the simulations was 0.005c/ωp and the time step, 0.003×1/ωp.
References
Tajima, T. & Dawson, J. M. Laser electron accelerator. Phys. Rev. Lett. 43, 267–270 (1979).
Mangles, S. P. D. et al. Electron acceleration from the breaking of relativistic plasma waves. Nature 431, 535–538 (2004).
Geddes, C. G. R. et al. High quality electron beams from a laser wakefield accelerator using plasma-channel guiding. Nature 431, 538–541 (2004).
Faure, J. et al. A laser-plasma accelerator producing monoenergetic electron beams. Nature 431, 541–544 (2004).
Pukhov, A. & Meyer-Ter-Vehn, J. Laser wake field acceleration: The highly non-linear broken wave regime. Appl. Phys. B 74, 355–361 (2002).
Leemans, W. P. et al. GeV electron beams from a centimetre-scale accelerator. Nature Phys. 2, 696–699 (2006).
Clayton, C. E. et al. Self-guided laser wakefield acceleration beyond 1 GeV using ionization-induced injection. Phys. Rev. Lett. 105, 105003 (2010).
Whittum, D. H. Electromagnetic-Instability of the ion-focused regime. Phys. Fluids B 4, 730–739 (1992).
Kostyukov, I., Kiselev, S. & Pukhov, A. X-ray generation in an ion channel. Phys. Plasmas 10, 4818–4828 (2003).
Rousse, A. et al. Production of a keV X-ray beam from synchrotron radiation in relativistic laser-plasma interaction. Phys. Rev. Lett. 93, 135005 (2004).
Wang, S. Q. et al. X-ray emission from betatron motion in a plasma wiggler. Phys. Rev. Lett. 88, 135004 (2002).
Johnson, D. K. et al. Positron production by X rays emitted by betatron motion in a plasma wiggler. Phys. Rev. Lett. 97, 175003 (2006).
Kneip, S. et al. Bright spatially coherent synchrotron X-rays from a table-top source. Nature Phys. 6, 980–983 (2010).
Nemeth, K. et al. Laser-driven coherent betatron oscillation in a laser-wakefield cavity. Phys. Rev. Lett. 100, 095002 (2008).
Mangles, S. P. D. et al. Laser-wakefield acceleration of monoenergetic electron beams in the first plasma-wave period. Phys. Rev. Lett. 96, 215001 (2006).
Jaroszynski, D. A. et al. Radiation sources based on laser-plasma interactions. Phil. Trans. R. Soc. A 364, 689–710 (2006).
Vainshtein, B. K. Diffraction investigation of the atomic-structure of matter. Acta Crystallogr. B 47, 145–154 (1991).
Sprangle, P., Esarey, E. & Ting, A. Nonlinear-interaction of intense laser-pulses in plasmas. Phys. Rev. A 41, 4463–4467 (1990).
Brunetti, E. et al. Low emittance, high brilliance relativistic electron beams from a laser-plasma accelerator. Phys. Rev. Lett. 105, 215007 (2010).
Wiggins, S. M. et al. High quality electron beams from a laser wakefield accelerator. Plasma Phys. Control. Fusion 52, 124032 (2010).
Pukhov, A., Gordienko, S., Kiselev, S. & Kostyukov, I. The bubble regime of laser-plasma acceleration: Monoenergetic electrons and the scalability. Plasma Phys. Control. Fusion 46, B179–B186 (2004).
Lu, W., Tzoufras, M. & Joshi, C. Generating multi-GeV electron bunches using single stage laser wakefield acceleration in a 3D nonlinear regime. Phys. Rev. 10, 061301 (2007).
Schlenvoigt, H. P. et al. A compact synchrotron radiation source driven by a laser-plasma wakefield accelerator. Nature Phys. 4, 130–133 (2008).
Jackson, J. D. Classical Electrodynamics (John Wiley, 1999).
Pukhov, A., Sheng, Z. M. & Meyer-ter-Vehn, J. Particle acceleration in relativistic laser channels. Phys. Plasmas 6, 2847–2854 (1999).
Reitsma, A. J. W. et al. Photon kinetic modeling of laser pulse propagation in underdense plasma. Phys. Plasmas 13, 113104 (2006).
Fonseca, R. A. et al. in Computational Science—ICCS 2002 (eds Peter, M. A., Sloot, A. G., Hoekstra, C. J., Kenneth Tan, J. J. & Dongarra,) 342–351 (Lecture Notes in Computer Science, Vol. 2331, Springer, 2002).
Hooker, C. J. et al. Conference on Lasers and Electro-Optics/Quantum Electronics and Laser Science Conference and Photonic Applications Systems Technologies, OSA Technical Digest (CD) paper JThB2 (Optical Society of America, 2008).
Hooker, S. M. et al. GeV plasma accelerators driven in waveguides. Plasma Phys. Control. Fusion 49, B403 (2007).
Glinec, Y. et al. Absolute calibration for a broad range single shot electron spectrometer. Rev. Sci. Instrum. 77, 103301 (2006).
Zeil, K. et al. Absolute response of Fuji imaging plate detectors to picosecond-electron bunches. Rev. Sci. Instrum. 81, 013307 (2010).
Llopart, X., Ballabriga, R., Campbell, M., Tlustos, L. & Wong, W. Timepix, a 65k programmable pixel readout chip for arrival time, energy and/or photon counting measurements. Nucl. Instrum. Methods A 581, 485–494 (2007).
Agostinelli, S. et al. GEANT4-a simulation toolkit. Nucl. Instrum. Methods A 506, 250–303 (2003).
Paterson, I. J., Clarke, R. J., Woolsey, N. C. & Gregori, G. Image plate response for conditions relevant to laser-plasma interaction experiments. Meas. Sci. Technol. 19, 095301 (2008).
Thompson, A. et al. X-ray Data Booklet 3rd edn Pub-490 Rev.3 (Lawrence Berkeley National Laboratory, 2009).
Acknowledgements
We acknowledge the support of the UK EPSRC, STFC, the Laserlab-Europe consortium and the Extreme Light Infrastructure (ELI) project. Over the past decade many current and previous members of the ALPHA-X consortium have made contributions to the project, for which we extend thanks. We also thank D. Clark and T. McCanny for their technical support, without which the project would not have been possible. The authors would like to thank the OSIRIS consortium (UCLA/IST) for the use of OSIRIS. The work of NRCL was partially supported by FCT Portugal through the grant SFRH/BD/37838/2007
Author information
Authors and Affiliations
Contributions
The experiment was conceived by D.A.J. The experiments and equipment calibration were undertaken by S.C., R.P.S, E.B., G.V., X.Y., R.C.I., S.M.W., G.H.W., M-P.A., D.M., R.M., G.S., M.H., D.J.H., N.R.C.L., V.O.S., J.M.D. and D.A.J. Theoretical analysis, interpretation and simulations were carried out by M.R.I., B.E., S.C. and D.A.J. The laser and target area operators were D.S. and P.P.R. The manuscript was prepared in the main by D.A.J., S.C., B.E. and M.R.I., with the reviewing and comment input of R.C.I., S.M.W., G.H.W., N.R.C.L. and J.M.D.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Cipiccia, S., Islam, M., Ersfeld, B. et al. Gamma-rays from harmonically resonant betatron oscillations in a plasma wake. Nature Phys 7, 867–871 (2011). https://doi.org/10.1038/nphys2090
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2090
This article is cited by
-
Non-linear QED approach for betatron radiation in a laser wakefield accelerator
Scientific Reports (2024)
-
High-flux bright x-ray source from femtosecond laser-irradiated microtapes
Communications Physics (2024)
-
Brilliant femtosecond-laser-driven hard X-ray flashes from carbon nanotube plasma
Nature Photonics (2023)
-
Femtosecond multimodal imaging with a laser-driven X-ray source
Communications Physics (2023)
-
Carbon nanotubes as outstanding targets for laser-driven particle acceleration
Nano Research (2023)