Abstract
Quantum mechanics permits an entity, such as an atom, to exist in a superposition of multiple states simultaneously. Quantum information processing (QIP) harnesses this profound phenomenon to manipulate information in radically new ways1. A fundamental challenge in all QIP technologies is the corruption of superposition in a quantum bit (qubit) through interaction with its environment. Quantum bang–bang control provides a solution by repeatedly applying ‘kicks’ to a qubit2, thus disrupting an environmental interaction. However, the speed and precision required for the kick operations has presented an obstacle to experimental realization. Here we demonstrate a phase gate of unprecedented speed3,4 on a nuclear spin qubit in a fullerene molecule, and use it to bang–bang decouple the qubit from a strong environmental interaction. We can thus trap the qubit in closed cycles on the Bloch sphere, or lock it in a given state for an arbitrary period. Our procedure uses operations on a second qubit, an electron spin, to generate an arbitrary phase on the nuclear qubit. We anticipate that the approach will be important for QIP technologies, especially at the molecular scale where other strategies, such as electrode switching, are unfeasible.
Similar content being viewed by others
Main
Two well-known concepts in overcoming the corruption of information stored within a qubit are decoherence-free subspaces5,6,7,8 and quantum-error-correcting codes9,10,11. The former is the passive solution of restricting oneself to some set of states that, owing to symmetries in the system, are largely immune to the dominant types of unwanted coupling. The latter is a sophisticated form of feedback control whereby the effect of unwanted coupling is detected and corrected. Between these limits there is the idea of dynamical suppression of coupling: making some rapid, low-level manipulation of the system so as to actively interfere with the decoherence process. Ideas here often relate to the ‘quantum Zeno effect’, in which repeated measurement (or some related process) is capable of suppressing the natural evolution of the system12,13. As the system evolves from one quantum eigenstate,  , to another,
, to another,  , it passes through a superposition state
, it passes through a superposition state  which, when measured, collapses to one of the two eigenstates with probabilities given by how far the system has been allowed to evolve. Therefore, if the measurements are made often, the system will have a high probability of being locked in the starting state (although, eventually, the finite probability of flipping will be realized).
which, when measured, collapses to one of the two eigenstates with probabilities given by how far the system has been allowed to evolve. Therefore, if the measurements are made often, the system will have a high probability of being locked in the starting state (although, eventually, the finite probability of flipping will be realized).
In a related technique that is part of the bang–bang family of strategies2,14, measurement operations are replaced by the application of rapid rotations on the superposition. The original bang–bang literature proposed the use of rapid bit flips to prevent unwanted phase evolution. Our implementation is very close in spirit to that original work: we perform the logical complement of the protocol, using rapid phase shifts to prevent amplitude evolution (see Fig. 1a and the video in the Supplementary Information). In many systems, energy loss is a primary decoherence mechanism; such decoherence would be suppressed by precisely this strategy.
a, Our decoupling process, shown by the path of the nuclear qubit on its Bloch sphere. The line within the Bloch sphere is a visual guide and does not indicate that the state becomes mixed. The state leaves the two-state space represented by the Bloch sphere, and returns at the indicated point on the opposite side, remaining pure at all times. A radiofrequency (RF) field is applied to drive state  to
to  . However, applying a phase of −1 to
. However, applying a phase of −1 to  during the evolution causes the state to jump to the other side of the Bloch sphere, from which it must evolve back to its initial state. The process can be repeated to prevent the system from ever reaching
during the evolution causes the state to jump to the other side of the Bloch sphere, from which it must evolve back to its initial state. The process can be repeated to prevent the system from ever reaching  . b, A model of the N@C60 molecule. c, Although this N@C60 system of S=3/2 electron spin and I=1 nuclear spin consists of 12 energy levels, we use only those four illustrated above. Nuclear Rabi oscillations are driven between
. b, A model of the N@C60 molecule. c, Although this N@C60 system of S=3/2 electron spin and I=1 nuclear spin consists of 12 energy levels, we use only those four illustrated above. Nuclear Rabi oscillations are driven between  and
and  , whereas the phase inversion is provided through a selective microwave pulse between
, whereas the phase inversion is provided through a selective microwave pulse between  and
and  . d, By driving both electron spin transitions simultaneously (with a single off-resonance pulse) an arbitrary phase can be applied between the
. d, By driving both electron spin transitions simultaneously (with a single off-resonance pulse) an arbitrary phase can be applied between the  and
and  states.
states.
This technique is distinct from the projective Zeno effect in two interesting respects. In addition to locking the system in one of the two eigenstates, the same sequence is capable of freezing any superposition state. Second, as the behaviour is always unitary, it remains deterministic even when the pulse frequency is limited. Given ideal pulses, one could trap the state in a closed cycle indefinitely.
We demonstrate this dynamic decoupling effect using a pair of coupled nuclear and electron spins in the endohedral fullerene molecule N@C60 (shown in Fig. 1b)15. Information on the origin of the 12-level spin system in N@C60 is provided in the Supplementary Information, along with other experimental details. We believe this system is the strongest candidate for a molecular qubit: the electron spin degree of freedom permits initialization to a genuine pure state, whereas the protection afforded by the fullerene armour yields the longest decoherence time measured for any molecular electron spin16,17,18. For the experiments described here, we chose four levels from the 12 present in such a way that they correspond to two qubits, an electron qubit (formed from MS=+3/2,−3/2) and a nuclear qubit (MI=+1,0), as shown in Fig. 1c. As the nuclear qubit has excellent natural environmental decoupling, we must introduce a strong coupling by applying a resonant radiofrequency field to drive Rabi oscillations. This field is then successfully decoupled by fast phase ‘kicks’ to the system: we exploit the qubit–qubit coupling, taking the electron qubit around closed cycles so as to apply phase shifts to the nuclear qubit. Finally, we observe that by detuning the microwave pulse away from the electron spin transition frequency, this technique can be generalized to apply an arbitrary phase gate to the nuclear spin on a timescale that is much faster than normal NMR methods.
The general pulse sequence used is shown in Fig. 2. A selective electron π-pulse on the MI=+1 manifold transfers the thermal polarization of the electron spin to the nuclear spin (this can be thought of as a controlled-NOT operation with the nucleus as control and electron as target19). The nuclear polarization then shows Rabi oscillations between the MI=0 and +1 levels (in Fig. 1  and
and  , respectively) on the application of a suitable radiofrequency driving field. During the Rabi oscillations, fast microwave pulses are applied on the electron spin to suppress the nuclear spin evolution. Finally, a measurement of the relevant state populations is performed using two-pulse electron spin echo detection.
, respectively) on the application of a suitable radiofrequency driving field. During the Rabi oscillations, fast microwave pulses are applied on the electron spin to suppress the nuclear spin evolution. Finally, a measurement of the relevant state populations is performed using two-pulse electron spin echo detection.
It is possible to apply a phase gate to a qubit by rotating one of the basis states around a complete cycle through an auxiliary level (Fig. 1c). This can be simply seen by evaluating the operator for a complete on-resonance rotation applied to a S=1/2 particle:

where σx is the Pauli spin matrix. Therefore, when this rotation is selectively performed on the  transition, state
transition, state  will acquire a phase of −1 with respect to
will acquire a phase of −1 with respect to  (that is, a π-phase shift). Although the electron spin used in this case is S=3/2, the Bloch vector for higher spin systems (in high-symmetry environments, such as our spherical fullerene) behaves identically to the S=1/2 case20,21.
(that is, a π-phase shift). Although the electron spin used in this case is S=3/2, the Bloch vector for higher spin systems (in high-symmetry environments, such as our spherical fullerene) behaves identically to the S=1/2 case20,21.
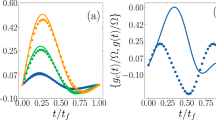
Figure 3a shows the effect of applying a π-phase shift during the nuclear Rabi oscillations: the evolution is reversed each time a microwave pulse is applied, as illustrated on the nuclear Bloch sphere in Fig. 3b. It is not necessary to apply perfect π-phase shifts to lock the spin. Implementation with smaller phase shifts are shown in Fig. 3c. After the first pulse, the nuclear spin evolves around a lesser circle on the Bloch sphere. A second (identical) phase shift brings the nuclear spin back onto a great circle, with an overall π-phase shift (illustrated in Fig. 3d). This kind of error cancellation is analogous to the 90y∘ 180x∘ 90y∘ type of pulse-correction NMR22,23. By increasing the repetition rate of the phase shift pulses, the nuclear spin evolution can be locked in one particular state (Fig. 3e) and released as desired (Fig. 3f).
Unperturbed Rabi oscillations are shown in black, whereas those under the influence of decoupling pulses are shown in red. The decay observed is an artefact of the inhomogeneity in the radiofrequency driving field and is not a true decoherence phenomenon. a,b, Microwave pulses are applied on the electron spin at regular intervals (indicated by arrows in a), inverting the phase of one of the nuclear spin states and reversing the evolution of the nuclear spin qubit. c,d, When we implement a phase shift of less than π, an odd–even behaviour is observed, corresponding to greater and lesser paths on the Bloch sphere. e, Increasing the repetition rate of the microwave pulses locks the system in a particular state. f, The qubit can be locked and released at any point.
Any microwave pulse of finite duration that is resonant with the primary  transition also performs a detuned excitation of the
transition also performs a detuned excitation of the  transition (illustrated in Fig. 4a). The difference between these two transition frequencies is fixed in our system by the hyperfine coupling constant a=15.8 MHz, but the effective detuning can be controlled through the microwave pulse power (B1). In the limit of strong selectivity (weak pulses) only the resonant transition is significantly excited and a complete cycle (
transition (illustrated in Fig. 4a). The difference between these two transition frequencies is fixed in our system by the hyperfine coupling constant a=15.8 MHz, but the effective detuning can be controlled through the microwave pulse power (B1). In the limit of strong selectivity (weak pulses) only the resonant transition is significantly excited and a complete cycle ( ) generates a π-phase shift in the nuclear qubit. Faster (non-selective) pulses are possible, provided that B1 is chosen such that both electron transitions undergo an integer number of complete cycles, thus ensuring the system returns to the subspace
) generates a π-phase shift in the nuclear qubit. Faster (non-selective) pulses are possible, provided that B1 is chosen such that both electron transitions undergo an integer number of complete cycles, thus ensuring the system returns to the subspace  after the microwave pulse. This permits the implementation of phase shifts that differ from π, as shown in Fig. 3c and d. The phase acquired by each cycle has a geometric interpretation: it is equal to half of the solid angle subtended by the path of an eigenstate around the Bloch sphere (see Fig. 4a)24. The differences in the two phases obtained defines the phase shift on the nuclear qubit.
after the microwave pulse. This permits the implementation of phase shifts that differ from π, as shown in Fig. 3c and d. The phase acquired by each cycle has a geometric interpretation: it is equal to half of the solid angle subtended by the path of an eigenstate around the Bloch sphere (see Fig. 4a)24. The differences in the two phases obtained defines the phase shift on the nuclear qubit.
Left: The path of the electron magnetization vector driven by a microwave field. Right: The corresponding z-magnetization. a, One transition is driven resonantly and one is strongly detuned. On each cycle, the phase accumulated is proportional to the area enclosed by the path. Both transitions must undergo an integer number of complete cycles to ensure the populations remain unchanged. b, With both transitions detuned by equal and opposite amounts, the population evolution for each is the same, whereas the phase accumulated is of opposite sign. Hence, the relative phase shift can be tuned by controlling the microwave pulse power.
A straightforward extension of this idea is to drive both the electron spin transitions ( and
and  ) with equal and opposite detuning (that is, at a frequency half-way between their resonances). Here, the condition of both transitions going through an integer number of complete cycles can be satisfied for any value of B1. The populations of both transitions evolve in the same way, whereas the phase acquired is opposite, as illustrated in Fig. 4b. The relative phase accumulated (which defines the phase gate applied) is determined only by B1, allowing an arbitrary phase gate to be applied on the nuclear spin (see also ref. 25). The duration of this gate (∼100 ns) is orders of magnitude shorter than typical NMR phase gates and about 105 times shorter than existing geometric phase gates in NMR3.
) with equal and opposite detuning (that is, at a frequency half-way between their resonances). Here, the condition of both transitions going through an integer number of complete cycles can be satisfied for any value of B1. The populations of both transitions evolve in the same way, whereas the phase acquired is opposite, as illustrated in Fig. 4b. The relative phase accumulated (which defines the phase gate applied) is determined only by B1, allowing an arbitrary phase gate to be applied on the nuclear spin (see also ref. 25). The duration of this gate (∼100 ns) is orders of magnitude shorter than typical NMR phase gates and about 105 times shorter than existing geometric phase gates in NMR3.
We have demonstrated an ultrafast phase gate on a nuclear spin qubit by driving a coupled electron qubit around a closed cycle. The gate speed can exceed even the nuclear precession frequency, which is only possible through exploiting the transition selection rules in the system. Through repeated application of this fast phase gate, we have bang–bang decoupled a nuclear spin qubit from a permanent driving field.
The experiments described here were performed on isolated N@C60 molecules in solution, in which the natural noise is low. The magnitude of interactions in an eventual fullerene-based processor will be at most that experienced by close-packed N@C60 arrays, where the nuclear spin dipole interaction is of the order of 100 Hz, or approximately 40 times weaker than the radiofrequency driving field we apply here. Paramagnetic impurities within such structures could increase the natural noise further; however, the speed of the decoupling gates demonstrated in our experiment show that interactions as strong as 100 kHz can be suppressed.
This scheme has a broad applicability: the minimum complexity required of a quantum system is three levels (the two qubit levels and one auxiliary level) coupled by a suitably rapid allowed transition. However, as we demonstrate here, the approach also works with more than three levels and several allowed transitions among those levels. Indeed, a very natural implementation will be any system with a coupled electron and nuclear spin, giving (in the S=1/2 case) four levels on two different energy scales. For example, two very different qubit systems also suited to our approach are phosphorous impurities in silicon and N–V centres in diamond. Both of these have been identified by the QIP community as promising qubits. In general, our demonstration highlights the potential benefits of physical ‘qubit’ systems beyond the simple two-level structure.
In addition to suppressing unwanted coupling to an environment, this effect is explicitly required in certain quantum computing schemes (for example, to control the interaction between neighbouring qubits in perpetually coupled spin chains26). Given the great difficulties associated with tailoring interactions in quantum systems, it is likely that decoupling strategies of this kind will form a quintessential element in real quantum computers.
References
Deutsch, D. Quantum-theory, the Church–Turing principle and the universal quantum computer. Proc. R. Soc. Lond. A 400, 97–117 (1985).
Viola, L. & Lloyd, S. Dynamical suppression of decoherence in two-state quantum systems. Phys. Rev. A 58, 2733–2744 (1998).
Jones, J. A., Vedral, V., Ekert, A. & Castagnoli, G. Geometric quantum computation using nuclear magnetic resonance. Nature 403, 869–871 (2000).
Vandersypen, L. M. et al. Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 414, 883–887 (2001).
Duan, L.-M. & Guo, G.-C. Preserving coherence in quantum computation by pairing quantum bits. Phys. Rev. Lett. 79, 1953–1956 (1997).
Zanardi, P. & Rasetti, M. Noiseless quantum codes. Phys. Rev. Lett. 79, 3306–3309 (1997).
Lidar, D., Chuang, I. L. & Whaley, K. B. Decoherence-free subspaces for quantum computation. Phys. Rev. Lett. 81, 2594–2597 (1997).
Kielpinski, D. et al. A decoherence-free quantum memory using trapped ions. Science 291, 1013–1015 (2001).
Shor, P. W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, 2493–2496 (1995).
Steane, A. M. Error correcting codes in quantum theory. Phys. Rev. Lett. 77, 793–797 (1996).
Knill, E. Quantum computing with realistically noisy devices. Nature 434, 39–44 (2005).
Facchi, P., Lidar, D. A. & Pascazio, S. Unification of dynamical decoupling and the quantum Zeno effect. Phys. Rev. A 69, 032314 (2004).
Itano, W. M., Heinzen, D. J., Bollinger, J. J. & Wineland, D. J. Quantum Zeno effect. Phys. Rev. A 41, 2295–2300 (1990).
Khodjasteh, K. & Lidar, D. Fault-tolerant quantum dynamical decoupling. Phys. Rev. Lett. 95, 180501 (2005).
Almeida-Murphy, T. et al. Observation of atomlike nitrogen in nitrogen-implanted solid C60 . Phys. Rev. Lett. 77, 1075–1078 (1996).
Ardavan, A. et al. Nanoscale solid-state quantum computing. Phil. Trans. R. Soc. Lond. A 361, 1473–1485 (2003).
Harneit, W. Fullerene-based electron-spin quantum computer. Phys. Rev. A 65, 032322 (2002).
Morton, J. J. L. et al. A new mechanism for electron spin echo envelope modulation. J. Chem. Phys. 122, 174504 (2005).
Mehring, M., Mende, J. & Scherer, W. Entanglement between an electron and a nuclear spin 1/2. Phys. Rev. Lett. 90, 153001 (2003).
Morton, J. J. L. et al. Measuring errors in single qubit rotations by pulsed electron paramagnetic resonance. Phys. Rev. A 71, 012332 (2005).
Schweiger, A. & Jeschke, G. Principles of Pulse Electron Paramagnetic Resonance (Oxford Univ. Press, New York, 2001).
Freeman, R. Spin Choreography: Basic Steps in High Resolution NMR (Spektrum, Oxford, UK, and Sausalito, USA, 1997).
Levitt, M. H. Composite pulses. Prog. Nucl. Magn. Reson. Spectrosc. 18, 61–122 (1986).
Aharonov, Y. & Anandan, J. Phase-change during a cyclic quantum evolution. Phys. Rev. Lett. 58, 1593–1596 (1987).
Schirmer, S. G., Oi, D. K. L. & Greentree, A. D. Controlled phase gate for solid-state charge-qubit architectures. Phys. Rev. A 71, 012325 (2005).
Benjamin, S. C., Lovett, B. W. & Reina, J. H. Optical quantum computation with perpetually coupled spins. Phys. Rev. A 70, 060305 (2004).
Acknowledgements
We acknowledge discussions with D. Oi and especially B. Lovett. We thank W. Harneit’s group at FU Berlin for providing nitrogen-doped fullerenes, and J. Dennis at QMUL, M. Austwick and G. Morley for the purification of N@C60. We thank the Oxford–Princeton Link fund for support. This research is part of the QIP IRC http://www.qipirc.org. J.J.L.M. is supported by St John’s College, Oxford. A.A. and S.C.B. are supported by the Royal Society. G.A.D.B. thanks the EPSRC for support (GR/S15808/01). Work at Princeton was supported by the NSF International Office through the Princeton MRSEC Grant No. DMR-0213706 and by the ARO and ARDA under Contract No. DAAD19-02-1-0040. Three-dimensional images were created using POV-Ray open-source software (http://www.povray.org).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary information: details of related movie (PDF 32 kb)
Supplementary Information
Supplementary materials and methods (PDF 89 kb)
Rights and permissions
About this article
Cite this article
Morton, J., Tyryshkin, A., Ardavan, A. et al. Bang–bang control of fullerene qubits using ultrafast phase gates. Nature Phys 2, 40–43 (2006). https://doi.org/10.1038/nphys192
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys192
This article is cited by
-
Quantum error correction of spin quantum memories in diamond under a zero magnetic field
Communications Physics (2022)
-
Coherent manipulation and quantum phase interference in a fullerene-based electron triplet molecular qutrit
npj Quantum Information (2021)
-
Engineering electronic structure to prolong relaxation times in molecular qubits by minimising orbital angular momentum
Nature Communications (2019)
-
Time-optimal control for hybrid systems based on the nitrogen-vacancy center
Control Theory and Technology (2017)
-
Generation of large coherent states by bang–bang control of a trapped-ion oscillator
Nature Communications (2016)