Abstract
Each successive generation of X-ray machines has opened up new frontiers in science, such as the first radiographs and the determination of the structure of DNA. State-of-the-art X-ray sources can now produce coherent high-brightness X-rays of greater than kiloelectronvolt energy and promise a new revolution in imaging complex systems on nanometre and femtosecond scales. Despite the demand, only a few dedicated synchrotron facilities exist worldwide, in part because of the size and cost of conventional (accelerator) technology1. Here we demonstrate the use of a new generation of laser-driven plasma accelerators2, which accelerate high-charge electron beams to high energy in short distances3,4,5, to produce directional, spatially coherent, intrinsically ultrafast beams of hard X-rays. This reduces the size of the synchrotron source from the tens of metres to the centimetre scale, simultaneously accelerating and wiggling the electron beam. The resulting X-ray source is 1,000 times brighter than previously reported plasma wigglers6,7 and thus has the potential to facilitate a myriad of uses across the whole spectrum of light-source applications.
Similar content being viewed by others
Main
There are a number of proposals to use extreme nonlinear interactions of the latest generation of high-power ultrashort-pulse laser systems to produce beams of high-energy photons with high brightness and short pulse duration. For example, high-order harmonic generation promises trains of coherent pulselets8 and Compton scattering could extend energies into the γ-regime9,10. An alternative proposal has been the use of compact laser–plasma accelerators to drive sources of undulating/wiggling radiation11.
These accelerators use the plasma wakefield generated by the passage of an intense laser pulse through an underdense plasma12. Such wakefields can have intrinsic fields of more than 1,000 times greater than the best achievable by conventional accelerator technology, and thus can accelerate particles to high energies in a fraction of the distance. Recently, it has been demonstrated that at high laser power, the wakefield can be driven to sufficient amplitude to be able to trap large numbers of particles (>100 pC) from the background plasma and accelerate them in a narrow energy spread beam3,4,5, now producing beams of electrons of gigaelectronvolt-scale energy of the order of 1 cm (refs 13, 14).
Such electron sources are of interest to replace the accelerators that drive current synchrotron sources, and typically use multiple periods of alternately poled magnets (undulators or wigglers) to reinforce the synchrotron emission over a length of a few metres. The first demonstrations of wakefield-driven radiation using external wigglers have also been reported, though still being limited to optical or near-optical wavelengths and modest peak brightness15,16.
However, the particles being accelerated in the plasma accelerator also undergo transverse (betatron) oscillations when subject to the focusing fields of the plasma wave. These oscillations occur at the betatron frequency  , where ωp is the plasma frequency and γ is the Lorentz factor of the electron beam17. As this betatron wavelength (λβ≈2π c/ωβ) is much smaller than the period of comparable external wigglers, again as a result of the extremely large electric fields of the wakefield, the wavelength at which these particles radiate (of order λ≈λβ/γ2) can be in the X-ray region for γ≳200, that is, for an electron beam of energy W>100 MeV. For small transverse amplitude and thus small strength parameter K=γ rβωβ/c≪1 (that is, undulator limit), the radiation spectrum will be narrowly peaked about a fundamental energy. As K
, where ωp is the plasma frequency and γ is the Lorentz factor of the electron beam17. As this betatron wavelength (λβ≈2π c/ωβ) is much smaller than the period of comparable external wigglers, again as a result of the extremely large electric fields of the wakefield, the wavelength at which these particles radiate (of order λ≈λβ/γ2) can be in the X-ray region for γ≳200, that is, for an electron beam of energy W>100 MeV. For small transverse amplitude and thus small strength parameter K=γ rβωβ/c≪1 (that is, undulator limit), the radiation spectrum will be narrowly peaked about a fundamental energy. As K 1, radiation also appears at harmonics. For large K≫1 (that is, large-amplitude wiggler limit) a synchrotron spectrum with broad emission consisting of closely spaced harmonics is produced17.
1, radiation also appears at harmonics. For large K≫1 (that is, large-amplitude wiggler limit) a synchrotron spectrum with broad emission consisting of closely spaced harmonics is produced17.

Here, I is the radiated energy, Nβ is the number of oscillations and Ecrit=3ℏK γ2ωβ is twice the energy above and below which roughly half of the total energy is radiated.  is a modified Bessel function of the second kind. For E>Ecrit, the spectrum of radiated energy decays exponentially. The radiation is confined to a cone with opening angle θ≈K/γ.
is a modified Bessel function of the second kind. For E>Ecrit, the spectrum of radiated energy decays exponentially. The radiation is confined to a cone with opening angle θ≈K/γ.
The first measurements of betatron radiation from a broad energy spread electron beam from a laser wakefield accelerator have demonstrated X-ray emission with energies up to ≃1 keV with a peak brightness up to 1019 photons per second per mrad2 per mm2 per 0.1% bandwidth6. Here we demonstrate that by entering the highly nonlinear, so-called bubble regime of laser wakefield acceleration2, we always and immediately inject a much larger amount of charge (>100 pC), which is accelerated to narrow-energy-spread beams with much higher peak energy (≃230 MeV over ≃5 mm) than in earlier experiments. This results in a 1–100 keV X-ray source with 1,000 times greater peak brightness than previous laser-driven betatron sources6,7. Furthermore, we demonstrate that the radiation has an appreciable degree of spatial coherence.
The experiment was carried out by focusing an intense short-pulse (≃30 fs, ≃2 J) laser onto the front edge of 3, 5 and 10 mm helium gas jets (see Methods). A scintillating screen was placed in the electron beam to measure its beam profile, and a permanent magnet spectrometer to measure its energy spectrum. Electron beams with narrow energy spread features were observed from all nozzles, at electron densities of 4–22×1018 cm−3. As there are consecutive phases of injection, the electron beam consists of multiple beamlets, which could be seen in both profile and spectral measurements14. For example, for an electron density of 8×1018 cm−3 on the 5 mm nozzle, electron beams of W=(230±70) MeV with ΔW/W=(25±10)% energy spread at full-width at half-maximum (FWHM) were observed with an average of 2.2±0.4 beamlets per shot, with a root-mean-square (r.m.s.) divergence of 1.5×1.8 mrad2 and r.m.s. pointing fluctuation of 4.8×4.7 mrad2. We typically measure 100–300 pC of charge in the beam. The average and maximum energy of the electron beam follow the typical wakefield electron density scaling law14,18.
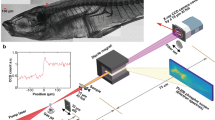
With the electron beam deflected away from laser axis by the spectrometer magnet, a bright (undeviated) beam of X-rays was also observed co-propagating along the laser axis. It was imperative to first prove that this X-ray source originates from the plasma itself. To do this a grid of silver wires (60 μm diameter, 310 μm separation) was placed a few centimetres from the target. X-rays originating from the interaction region project the outline of the mesh onto an imaging plate. A strongly directional beam of X-rays is evident in Fig. 1a. When either the laser power or electron plasma density was reduced to inhibit the electron beam, the X-ray beam also disappeared, showing that the generation of the X-rays is linked to the electron beam. The profile is elliptical, with a FWHM divergence of θx×θy=4×13 mrad2, corresponding to a wiggler parameter K=θ γ of Kx=1.5 and Ky=5 for a simultaneously measured electron beam energy W=200 MeV. The X-ray beam pointing is extremely stable, as can be deduced from Fig. 1b, which shows the sum of five consecutive shots. Their combined divergence is not significantly larger than that of a single-shot measurement, the r.m.s. pointing stability is 5 mrad in the horizontal and vertical direction, similar to the pointing stability of the electron beam.
a,b, Single-shot X-ray beam profile (a) and sum of five consecutive shot profiles (b) show the imprint of a wire grid and a 4×13 mrad2 beam with 5 mrad pointing stability. c–h, X-ray radiographic images of wire triplets and a resolution test target. The objects contain features as small as 3 μm, which are resolved on the radiographs, indicating a betatron source of size ≤3 μm. i,j, Photographic images of the smallest wire triplet and resolution test target, from which the various feature sizes were obtained.
To give an indication of the X-ray source size, microscopic objects were backlit with the X-ray beam. Figure 1c–h shows X-ray radiographic images of wire triplets of various sizes and of a resolution test target. Figure 1i,j gives photographic images of the smallest wire triplet and the test target. Even the smallest features of size 3 μm are resolved, indicating that the betatron X-ray source is ≲3 μm, smaller than the size of the plasma wave in which the radiating electrons were trapped and oscillate (≃20 μm diameter).
To quantify the source size more precisely, a half-plane was backlit with the X-ray beam. A typical intensity distribution on the detector looks like a half-shadow (Fig. 2a inset), whose details convolve information about the X-ray source and half-plane. The half-plane was a 0.25-mm-thick cleaved InSb crystal (<6% transmission below 20 keV) and resembles an ideal step function.
a, Close-up of measured intensity distribution (black squares) integrated along the edge of the half-shadow (inset) and exemplary intensity distributions using Fresnel diffraction modelling, for a source with Gaussian intensity distribution and synchrotron spectrum Ecrit/wx of 8 keV/1 μm (solid red), 8 keV/3 μm (dashed green), 2 keV/1 μm (dash–dotted blue) and 8 keV/6 μm (dotted grey). b, Series of measured intensity distributions corresponding to shots with decreasing source size wx (from modelling) and fringe visibility. The numbers are the 95% confidence interval of the source size determined by a least-squares fit. c, The experimentally obtained fringe visibility is consistent with the fringe visibility obtained from the modelling, plotted for a 6–10 keV synchrotron spectrum with spatial profile of (super-) Gaussian to top-hat type. Horizontal error bars are given by the fitting procedure (typically ±30–40%) and vertical error bars are due to the noise in the experimental data (typically ±0.03–0.04).
To accurately model the shape of the intensity distribution, it is necessary to use Fresnel diffraction (see Methods), where the details of the diffraction pattern depend on the spatial and spectral intensity distribution of the source and the dimensions of the set-up. Figure 2a shows a close-up of a typical experimental and several modelled intensity distributions based on a Gaussian intensity profile and synchrotron spectrum. For the solid red curve in Fig. 2a, Ecrit=8 keV and a 1/e2 intensity radius wx=1 μm was assumed, which best reproduced both the sharp rise and the amplitude and width of the first fringe. Changing wx or Ecrit under or overestimates the height and/or width of the overshoot and/or the rise, as shown by the other curves in Fig. 2.
To obtain a 95% confidence interval for the source size, a least-squares fit based on the Fresnel model was carried out with the measured intensity distributions (see Methods). Figure 2a shows exemplarily that the agreement between model and data depends only weakly on the critical energy. This was confirmed by independent measurements of the spectrum at identical experimental conditions, which found Ecrit=6–10 keV, as discussed later. To accurately acknowledge the small uncertainty in critical energy and also possible deviations from a Gaussian source profile, the parameter space of the Fresnel model includes spectra with critical energies 6–10 keV and spatial profiles of (super-) Gaussian to top-hat type.
Figure 2b shows a series of experimental intensity distributions for which the source size was determined in this way. By changing the plasma density, we have some level of control over the source size. As the source size increases the visibility of the first Fresnel fringe decreases. This is in accordance with the modelling, from which it is expected that the fringes disappear for a source size wx≳5 μm.
For the ringing to occur, the radiation needs to have an appreciable degree of spatial coherence at the place of the half-plane, which is merely u=50 mm from the source. The van Cittert–Zernike theorem states that even the radiation of uncorrelated emitters with Gaussian intensity distribution can be spatially coherent19. The transverse coherence length is given by Ltrans=λ u/2π wx,y. In our case the relevant radiation wavelength is λ≃6×10−10 m, which is the peak of the product of the synchrotron spectrum Ecrit≃8 keV and detector response. For a source size of wx=2 μm, Ltrans≃3 μm, which is enough to observe one Fresnel fringe. The spectral width of the source also reduces fringe visibility, as the temporal or longitudinal coherence length Llong=λ2/2Δλ≃λ.
We have assessed the amount of coherence by calculating the experimental fringe contrast (Imax−Imin)/(Imax+Imin) and comparing it with the prediction from the modelling of a (super-) Gaussian to top-hat source with Ecrit=6–10 keV, as shown in Fig. 2c. From this agreement we infer that the complex coherence factor μ of our betatron source must be close to the theoretical upper limit of μ=0.88, which would be achievable for a Gaussian intensity distribution19.
The spectral properties of the betatron radiation were determined by measuring the X-ray transmission through a set of filters (see the inset of Fig. 3a) with an X-ray CCD (charge-coupled device) detector7. Assuming the spectrum is synchrotron-like, the measured Ecrit is (29±13) keV for ne=(1.0±0.4)×1019 cm−3, and the 5 mm nozzle (see Fig. 3a). With twice the density and half the laser power, the measured Ecrit=6–10 keV is found to be lower, consistent with what can be inferred from the fringe measurement (Ecrit=4–16 keV) that was carried out at these conditions.
a, The modelled, normalized betatron spectrum agrees well with the experimentally measured spectrum obtained within one standard deviation. Inset: The experimental spectrum is inferred from measurements of the X-ray yield through various filters with known transmission. b, The angularly and spectrally resolved X-ray flux displays a peak on axis at 10 keV and a tail extending to ≃100 keV. c, The spectrally integrated X-ray beam profile shows an elliptically elongated beam profile in the direction of laser polarization.
Numerical modelling was carried out using electron trajectories obtained from the fully relativistic particle-in-cell code OSIRIS. The simulations were run in the boosted frame, which, because of relativistic length contraction and time dilation, offers higher resolutions for shorter run times. The trajectories were post-processed to yield the characteristics of the betatron radiation (see Methods). Figure 3b shows the modelled X-ray spectrum as a function of energy and angle. The X-ray flux peaks on-axis at 10 keV and extends to ≃100 keV. A lineout taken on-axis, as would be measured by our detector, is plotted in Fig. 3a, comparing well with the measured spectrum. A total of 108 photons are predicted between 1 and 84 keV. We measure 106–108, depending on electron charge and (albeit small) pointing fluctuation. As a result of the difficulty in decoupling pointing and yield fluctuations, we take conservatively 5×107 photons, a 1/e2 source radius wx,y=1 μm, a divergence of 13×4 mrad2, a bandwidth of 100% and a pulse duration of 30 fs (refs 20, 21). This gives a maximum achieved peak brightness of 1×1022 photons per second per mrad2 per mm2 per 0.1% bandwidth.
The modelling reveals that the fastest electrons oscillate with the smallest amplitudes rβ≲2 μm, consistent with the measured source sizes. K-parameters range from 1 to 30 with an average ≃7, close to the measured experimental value. Figure 3c shows the spectrally integrated X-ray beam profile obtained from the modelling for a 5 mm nozzle at ne=8×1018 cm−3. The profile is elongated in the direction of laser polarization and the divergence 5×16 mrad2 is in excellent quantitative agreement with the measurement (Fig. 1a).
The measured radiation is bright, spatially coherent and intrinsically ultrafast, opening up a multitude of advanced applications, such as phase contrast and lensless imaging, previously possible only with large conventional light sources22,23. The laser plasma wiggler has the potential for making high-brightness radiation sources widespread, and thus impacting all areas of science and technology.
Methods
Laser.
The experiments were carried out on the Hercules laser at the University of Michigan. Linearly polarized pulses with a central wavelength of λ0=800 nm, a Gaussian FWHM pulse duration of τ=32 fs and a maximum energy of 2.3 J were focused to a peak intensity of I=4.7×1019 W cm−2 or normalized vector potential a0=4.7 with an off-axis parabolic mirror of focal length f=1 m and F-number of F=10. The transverse intensity profile of the laser in vacuum yields a focal spot diameter of dFWHM=11.2 μm. Typically 55% of the pulse energy is within dFWHM.
Fresnel diffraction.
Fresnel diffraction occurs when a wave passes through an aperture and diffracts in the near field, causing any diffraction pattern observed to differ in size and shape, depending on the distance between the aperture and the projection v, the size of the aperture A and the wavelength of the wave λ. In the present case, v≃1,500 mm, λ<5×10−7 mm (>2 keV) and a≃125 μm assuming an X-ray beam of 5 mrad divergence and a half-plane aperture at u=50 mm from the source. Therefore the Fresnel number F=A2/(v λ)≃16>1, requiring a treatment in the Fresnel regime. u and v are the object and image distance respectively. The intensity distribution of a monochromatic point source on the projection is given by19

where E and E* are the electric field and its complex conjugate,  and
and  are the Fresnel functions,
are the Fresnel functions,  and x is the position on the projection. If the source is not point-like, the electric field has to be convolved with the source function and spectral distribution
and x is the position on the projection. If the source is not point-like, the electric field has to be convolved with the source function and spectral distribution  to compute I(x), where R(λ) is the spectral response of the detector. The Fresnel intensity distribution can be modelled with a simple error function, which, for a given spectrum and profile, results in a relationship between the source size and the width of the error function. This can be used to determine the source size from the experimental data by applying a least-squares method.
to compute I(x), where R(λ) is the spectral response of the detector. The Fresnel intensity distribution can be modelled with a simple error function, which, for a given spectrum and profile, results in a relationship between the source size and the width of the error function. This can be used to determine the source size from the experimental data by applying a least-squares method.
Numerical modelling.
Three-dimensional numerical simulations were carried out with the particle-in-cell code OSIRIS (ref. 24), in which a linearly polarized pulse with experimental parameters is focused 0.25 mm into the plasma. The electron plasma density profile increases linearly from zero to ne=8×1018 cm−3 in the first 0.5 mm, is then constant for 3.5 mm and finally falls linearly to zero in 0.5 mm. Simulations were carried out in a relativistically boosted frame (γ=5), which allows for significant computational gains25,26. The simulation box corresponds to 60×94×94 μm3in the laboratory frame. A total of 9.2×108 particles (2 per cell) were pushed for 5×103 iterations. The resolution in the laser propagation direction z is k0Δz=0.11, and kpΔx=kpΔy=0.16 in the transverse directions. To obtain the radiation emission from the simulation, a post-processing diagnostic is used on a set of trajectories of injected electrons27. The position and momentum history of the electrons is used to deposit the radiated fields on a virtual detector.
Change history
02 September 2011
This paper presents the realization and comprehensive characterization of a compact bright source of ultrafast synchrotron radiation with appreciable degree of spatial coherence. It has been drawn to our attention that we had inadvertently neglected to cite some prior works that described selected aspects of the betatron radiation in similar experimental configurations: ref. 1 describes a direct source size measurement based on Fresnel diffraction from laser-based synchrotron radiation demonstrating the resolution that this measurement can yield, and refs 2 and 3 describe indirect measurements of the electron oscillation amplitude based on far-field analysis of the betatron profile and based on the linking of electron and X-ray spectra, respectively. The varied techniques of refs 1–3 give consistent answers for the X-ray source size. Refs 1–3 are consistent with our measurement and modelling. They underline the importance in our experiment to generate high-charge quasi-monoenergetic electron beams to scale up betatron energy and brightness whilst keeping the source size small.
References
Bilderback, D. H., Elleaume, P. & Weckert, E. Review of third and next generation synchrotron light sources. J. Phys. B 38, 773–797 (2005).
Pukhov, A. & Meyer-ter Vehn, J. Laser wake field acceleration: The highly non-linear broken-wave regime. Appl. Phys. B 74, 355–361 (2002).
Mangles, S. P. D. et al. Monoenergetic beams of relativistic electrons from intense laser–plasma interactions. Nature 431, 535–538 (2004).
Geddes, C. G. R. et al. High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding. Nature 431, 538–541 (2004).
Faure, J. et al. A laser–plasma accelerator producing monoenergetic electron beams. Nature 431, 541–544 (2004).
Rousse, A. et al. Production of a kev X-ray beam from synchrotron radiation in relativistic laser–plasma interaction. Phys. Rev. Lett. 93, 135005 (2004).
Kneip, S. et al. Observation of synchrotron radiation from electrons accelerated in a petawatt-laser-generated plasma cavity. Phys. Rev. Lett. 100, 105006 (2008).
Dromey, B. et al. High harmonic generation in the relativistic limit. Nature Phys. 2, 456–459 (2006).
Schoenlein, R. W. et al. Femtosecond X-ray pulses at 0.4 Å generated by 90° Thomson scattering: A tool for probing the structural dynamics of materials. Science 274, 236–238 (1996).
Zh Esirkepov, T., Bulanov, S. V., Kando, M., Pirozhkov, A. S. & Zhidkov, A. G. Boosted high-harmonics pulse from a double-sided relativistic mirror. Phys. Rev. Lett. 103, 025002 (2009).
Kiselev, S., Pukhov, A. & Kostyukov, I. X-ray generation in strongly nonlinear plasma waves. Phys. Rev. Lett. 93, 135004 (2004).
Tajima, T. & Dawson, J. M. Laser electron-accelerator. Phys. Rev. Lett. 43, 267–270 (1979).
Leemans, W. P. et al. GeV electron beams from a centimetre-scale accelerator. Nature Phys. 2, 696–699 (2006).
Kneip, S. et al. Near-GeV acceleration of electrons by a nonlinear plasma wave driven by a self-guided laser pulse. Phys. Rev. Lett. 103, 035002 (2009).
Schlenvoigt, H. P. et al. A compact synchrotron radiation source driven by a laser–plasma wakefield accelerator. Nature Phys. 4, 130–133 (2008).
Fuchs, M. et al. Laser-driven soft-X-ray undulator source. Nature Phys. 5, 826–829 (2009).
Esarey, E., Shadwick, B. A., Catravas, P. & Leemans, W. P. Synchrotron radiation from electron beams in plasma-focusing channels. Phys. Rev. E 65, 056505 (2002).
Lu, W. et al. Generating multi-GeV electron bunches using single stage laser wakefield acceleration in a 3d nonlinear regime. Phys. Rev. ST Accel. Beams 10, 061301 (2007).
Born, M. & Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light 7th edn (Cambridge Univ. Press, 1999).
Mangles, S. P. D. et al. Laser-wakefield acceleration of monoenergetic electron beams in the first plasma-wave period. Phys. Rev. Lett. 96, 215001 (2006).
Debus, A. D. et al. Electron bunch length measurements from laser-accelerated electrons using single-shot THz time-domain interferometry. Phys. Rev. Lett. 104, 084802 (2010).
Neutze, R., Wouts, R., van der Spoel, D., Weckert, E. & Hajdu, J. Potential for biomolecular imaging with femtosecond X-ray pulses. Nature 406, 752–757 (2000).
Wilkins, S. W., Gureyev, T. E., Gao, D., Pogany, A. & Stevenson, A. W. Phase-contrast imaging using polychromatic hard X-rays. Nature 384, 335–338 (1996).
Fonseca, R. A. et al. Lecture Notes in Computer Science, Vol. 2331 342–351 (Springer, 2002).
Vay, J. L. Noninvariance of space- and time-scale ranges under a Lorentz transformation and the implications for the study of relativistic interactions. Phys. Rev. Lett. 98, 130405 (2007).
Martins, S. F., Fonseca, R. A., Lu, W., Mori, W. B. & Silva, L. O. Exploring laser-wakefield-accelerator regimes for near-term lasers using particle-in-cell simulation in Lorentz-boosted frames. Nature Phys. 6, 311–316 (2010).
Martins, J. L., Martins, S. F., Fonseca, R. A. & Silva, L. O. Harnessing Relativistic Plasma Waves as Novel Radiation Sources from Terahertz to X-Rays and Beyond, vol. 7359 73590V (SPIE, 2009).
Acknowledgements
S.K. acknowledges C. Spindloe for assistance with target preparation and the Euroleap network for financial assistance. This work was partially supported by the US National Science Foundation through the Physics Frontier Center FOCUS Grant No. PHY-0114336 and the NSF/DNDO Grant No. 0833499. The work of J.L.M., S.F.M., R.F. and L.O.S. is partially supported by FCT (Portugal), and Laserlab-Europe/LAPTECH, EC FP7 Contract No. 228334.
Author information
Authors and Affiliations
Contributions
The experiment and analysis was carried out in the main by S.K. and C.M. with contributions from C.B., F.D., C.H., S.P.D.M., T.M., S.R.N., and C.A.J.P. Simulations were carried out by J.L.M., S.F.M., R.F. and L.O.S., V.Y., G.K. and V.C. operated the laser, S.K., K.K., S.P.D.M., A.M., Z.N., K.T.P., J.S., A.G.R.T. contributed to planning, interpretation and manuscript preparation.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Kneip, S., McGuffey, C., Martins, J. et al. Bright spatially coherent synchrotron X-rays from a table-top source. Nature Phys 6, 980–983 (2010). https://doi.org/10.1038/nphys1789
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1789
This article is cited by
-
Coherence and superradiance from a plasma-based quasiparticle accelerator
Nature Photonics (2024)
-
Non-linear QED approach for betatron radiation in a laser wakefield accelerator
Scientific Reports (2024)
-
High-flux bright x-ray source from femtosecond laser-irradiated microtapes
Communications Physics (2024)
-
Narrow bandwidth, low-emittance positron beams from a laser-wakefield accelerator
Scientific Reports (2024)
-
Shaped liquid drops generate MeV temperature electron beams with millijoule class laser
Communications Physics (2024)