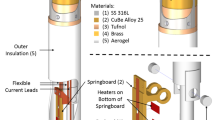
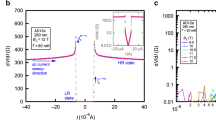
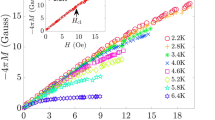
Abstract
The interface properties of high-temperature (high-Tc) copper oxide superconductors have been of interest for many years, and play an essential role in Josephson junctions, superconducting cables and microwave electronics. In particular, the maximum critical current achievable in high-Tc wires and tapes is well known to be limited by the presence of grain boundaries, regions of mismatch between crystallites with misoriented crystalline axes. Studies of single artificially fabricated grain boundaries have revealed that the critical current Jc of a grain boundary junction depends exponentially on the misorientation angle. Until now microscopic understanding of this apparently universal behaviour has been lacking. We present here the results of a microscopic evaluation based on a construction of fully three-dimensional YBa2Cu3O7−δ grain boundaries using molecular dynamics. With these structures, we calculate an effective tight-binding Hamiltonian for the d-wave superconductor with a grain boundary. The critical current is then shown to follow an exponential suppression with grain boundary angle α. We identify the build-up of charge inhomogeneities as the dominant mechanism for the suppression of the supercurrent.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
References
Hilgenkamp, H. & Mannhart, J. Grain boundaries in high-Tc superconductors. Rev. Mod. Phys. 74, 485–549 (2002).
Dimos, D., Chaudhari, P., Mannhart, J. & LeGoues, F. K. Orientation dependence of grain-boundary critical currents in YBa2Cu3O7−δ bicrystals. Phys. Rev. Lett. 61, 219–222 (1988).
Chaudhari, P., Dimos, D. & Mannhart, J. in Earlier and Recent Aspects of Superconductivity (eds Bednorz, J. G. & Müller, K. A.) 201–207 (Springer, 1990).
Sigrist, M. & Rice, T. M. Paramagnetic effect in high Tc superconductors —a hint for d-wave superconductivity. J. Phys. Soc. Jpn 61, 4283–4286 (1992).
Sigrist, M. & Rice, T. M. On the phenomenology of superconductivity in cuprate materials. J. Low Temp Phys. 95, 389–393 (1994).
Yokoyama, T., Sawa, Y., Tanaka, Y. & Golubov, A. A. Angular dependence of Josephson currents in unconventional superconducting junctions. Phys. Rev. B 75, 020502(R) (2007).
Gurevich, A. & Pashitskii, E. A. Current transport through low-angle grain boundaries in high-temperature superconductors. Phys. Rev. B. 57, 13878–13893 (1998).
Stolbov, S. V., Mironova, M. K. & Salama, K. Microscopic origins of the grain boundary effect on the critical current in superconducting copper oxides. Supercond. Sci. Technol. 12, 1071–1074 (1999).
Pennycook, S. J. et al. in Studies of High Temperature Superconductors: Microstructures and Related Studies of High Temperature Superconductors-II Vol. 30 (ed. Narlikar, A. V.) Ch. 6 (Nova Science Publishers, 2000).
Hu, C-R. Midgap surface states as a novel signature for d x a 2 − x b 2 -wave superconductivity. Phys. Rev. Lett. 72, 1526–1529 (1993).
Tanaka, Y. & Kashiwaya, S. Theory of tunneling spectroscopy of d-wave superconductors. Phys. Rev. Lett. 74, 3451–3454 (1994).
Löfwander, T., Shumeiko, V. S. & Wendin, G. Andreev bound states in high-Tc superconducting junctions. Supercond. Sci. Technol. 14, R53–R77 (2001).
Tanaka, Y. & Kashiwaya, S. Theory of the Josephson effect in d-wave superconductors. Phys. Rev. B 53, R11957–R11960 (1996).
Barash, Yu. S., Burkhardt, H. & Rainer, D. Low-temperature anomaly in the Josephson critical current of junctions in d-wave superconductors. Phys. Rev. Lett. 77, 4070–4073 (1996).
Tanaka, Y. & Kashiwaya, S. Theory of Josephson effects in anisotropic superconductors. Phys. Rev. B 56, 892–912 (1997).
Baetzold, R. C. Atomistic simulation of ionic and electronic defects in YBa2Cu3O7 . Phys. Rev. B 38, 11304–11312 (1988).
Zhang, X. & Catlow, C. R. A. Molecular dynamics study of oxygen diffusion in YBa2Cu3O6.91 . Phys. Rev. B 46, 457–462 (1992).
Liu, P. & Wang, Y. Theoretical study on the structure of Cu(110)-p2×1–O reconstruction. J. Phys. Condens. Matter 12, 3955–3966 (2000).
Phillpot, S. R. & Rickman, J. M. Simulated quenching to the zero-temperature limit of the grand-canonical ensemble. J. Chem. Phys. 97, 2651–2659 (1992).
Slater, J. C. & Koster, G. F. Simplified LCAO method for the periodic potential problem. Phys. Rev. 94, 1498–1524 (1954).
Harrison, W. A. Electronic Structure and the Properties of Solids (Dover Publications, 1989).
Chmaissem, O., Eckstein, Y. & Kuper, C. G. The structure and a bond-valence-sum study of the 1-2-3 superconductors (CaxLa1−x)(Ba1.75−xLa0.25+x)Cu3Oy and YBa2Cu3Oy . Phys. Rev. B 63, 174510 (2001).
Brown, I. D. A determination of the oxidation states and internal stress in Ba2YCu3Ox, x=6−7 using bond valences. J. Solid State Chem. 82, 122–131 (1989).
Zhang, F. C. & Rice, T. M. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 37, 3759–3761 (1988).
Andersen, B. M., Bobkova, I., Barash, Yu. S. & Hirschfeld, P. J. 0–π transitions in Josephson junctions with antiferromagnetic interlayers. Phys. Rev. Lett. 96, 117005–117008 (2006).
Freericks, J. K. Transport in Multilayered Nanostructures. The Dynamical Mean-Field Theory Approach (Imperial College Press, 2006).
Andersen, B. M., Barash, Yu. S., Graser, S. & Hirschfeld, P. J. Josephson effects in d-wave superconductor junctions with antiferromagnetic interlayers. Phys. Rev. B 77, 054501 (2008).
Lee, S. et al. Weak-link behavior of grain boundaries in superconducting Ba(Fe1−xCox)2As2 bicrystals. Appl. Phys. Lett. 95, 212505 (2009).
Hammerl, G. et al. Possible solution of the grain-boundary problem for applications of high-Tc superconductors. Appl. Phys. Lett. 81, 3209–3211 (2002).
Acknowledgements
This work was supported by DOE grant DE-FG02-05ER46236 (P.J.H.), and by the DFG through SFB 484 and TRR 80 (S.G., T.K., R.G. and J.M.) and a research scholarship (S.G.). We are grateful to Yu. S. Barash for important early contributions to the project and we acknowledge fruitful discussions with A. Gurevich and F. Loder. P.J.H. would also like to thank the Kavli Institute for Theoretical Physics for support under NSF-PHY05-51164 during the writing of this manuscript. The authors acknowledge the University of Florida High-Performance Computing Center for providing computational resources and support that have contributed to the research results reported in this article.
Author information
Authors and Affiliations
Contributions
R.G. applied the Slater–Koster technique to derive an effective tight-binding model Hamiltonian at the grain boundary and B.M.A. contributed in setting up the Bogoliubov–de Gennes equations for the calculation of the critical current. S.G. carried out the numerical calculations under the supervision of P.J.H. and T.K. J.M. contributed with his experience and knowledge about grain boundaries and the physical length scales involved. All authors contributed to the analysis of the results. P.J.H., T.K., J.M. and S.G. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 862 kb)
Rights and permissions
About this article
Cite this article
Graser, S., Hirschfeld, P., Kopp, T. et al. How grain boundaries limit supercurrents in high-temperature superconductors. Nature Phys 6, 609–614 (2010). https://doi.org/10.1038/nphys1687
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1687
This article is cited by
-
Effect of body defect on mechanical behaviors of Cu nanowire under tension: a molecular dynamics investigation
Journal of Materials Science (2017)
-
An Exponential Model for Critical Current Density Through a Low-Angle Grain Boundary in a High-T c Superconductor
Journal of Superconductivity and Novel Magnetism (2016)
-
Flux-Pinning-Induced Stress and Deformation Analyses of a Long Rectangular Superconducting Bicrystal
Journal of Superconductivity and Novel Magnetism (2016)
-
Effect of an Elliptical Inclusion on Critical Current Density of a Long Cylindrical High-T c Superconductor
Journal of Superconductivity and Novel Magnetism (2016)
-
Recent Achievements on the Physics of High-T C Superconductor Josephson Junctions: Background, Perspectives and Inspiration
Journal of Superconductivity and Novel Magnetism (2013)