Abstract
The origin of the superconducting state in the recently discovered Fe-based materials1,2,3 is the subject of intense scrutiny. Neutron scattering4,5,6,7 and NMR (ref. 8) measurements have already demonstrated a strong correlation between magnetism and superconductivity. A central unanswered question concerns the nature of the normal-state spin fluctuations that may be responsible for the pairing. Here we present inelastic neutron scattering measurements from large single crystals of superconducting and non-superconducting Fe1+yTe1−xSex. These measurements indicate a spin fluctuation spectrum dominated by two-dimensional incommensurate excitations extending to energies greater than 250 meV. Most importantly, the spin excitations in Fe1+yTe1−xSex have four-fold symmetry about the (1, 0) wavevector (square-lattice (π,π) point). Moreover, the excitations are described by the identical wavevector and can be characterized by the same model as the normal-state spin excitations in the high-TC cuprates9,10,11. These results demonstrate commonality between the magnetism in these classes of materials, which perhaps extends to a common origin for superconductivity.
Similar content being viewed by others
Main
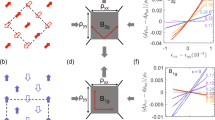
The discovery of superconductivity in LaFeAsO1−xFx with TC=28 K (ref. 1) sparked a flurry of scientific activity and TC rapidly increased to ∼55 K on replacing La with other rare-earth elements2,12,13. In addition to the RFeAsO family of compounds, superconductivity was also discovered in AFe2As2 (ref. 3), LiFeAs (ref. 14), and in the alpha phase of Fe1+yTe1−xSex (refs 15, 16). These materials share common structural square layers with Fe coordinated with either a pnictogen or a chalcogen. The unit cell contains two Fe atoms generating a reciprocal space rotated by 45∘ from the conventional square lattice (see Fig. 1a). In RFeAsO and AFe2As2, the parent compounds show long-range spin-density-wave order characterized by the wavevector Q=(1/2,1/2,L) (refs 17, 18, 19). Doping suppresses magnetic order, allowing superconductivity to emerge with the concomitant appearance of a resonance in the spin fluctuation spectrum4,5,6,7. However, the resonance probably contains only a small fraction of the total magnetic spectral weight and, consequently, understanding the role magnetism has in the superconductivity requires a detailed understanding of the higher energy spectrum of magnetic excitations.
The black (red) labels represent wavevectors in the tetragonal (square) reciprocal lattice. The red circles indicate the square-lattice (π,0) points where the resonance is observed and the green squares indicate the square-lattice (π,π) points. a, The dashed blue line denotes the Brillouin zone of the P4/n m m crystal structure. For the Fe sublattice, (1, 0) is no longer a zone centre and the Brillouin zone becomes larger, as represented by the black dashed line. b, The same diagram as in a, but centred at (1, 0). The blue ovals show the location of the observed excitations and the arrows represent the direction of dispersion with increasing energy transfer. The distance from (1, 0) is indicated by δ.
The Fe1+yTe1−xSex materials are ideal candidates for a study of the magnetic excitations as large single crystals, necessary for detailed inelastic neutron scattering studies, may be grown. However, these materials differ from other Fe-based superconductors in that the Fe1+yTe endpoint member (for small y) orders magnetically with a structure described by the wavevector (1/2, 0, 1/2) (ref. 20) as opposed to (1/2, 1/2, L). Despite this difference, superconducting samples of Fe1+yTe1−xSex with higher Se content show a magnetic resonance at the same (1/2, 1/2) wavevector as other Fe-based superconductors7,21 suggesting commonality in the magnetic response. To explore the magnetic excitations, inelastic neutron scattering measurements were carried out using the MERLIN spectrometer at the ISIS neutron scattering facility and the ARCS spectrometer at the Spallation Neutron Source. Measurements of lower energy excitations were carried out using the HB1 and HB3 triple-axis spectrometers at the High Flux Isotope Reactor. The single-crystal samples of Fe1.04Te0.73Se0.27 and FeTe0.51Se0.49 studied here were prepared as in ref. 22. Bulk measurements indicate weak, probably filamentary, superconductivity in Fe1.04Te0.73Se0.27 and bulk superconductivity in FeTe0.51Se0.49. Neither sample shows long-range magnetic order; however, for x=0.27, short-range magnetic order is observed20.
Figure 2a–h summarizes the measured magnetic excitations at several energy transfers for both the x=0.27 and x=0.49 samples. We first note that the observed spectrum of magnetic excitations is two-dimensional (2D) in nature. Measurements at multiple sample-rotation angles were combined to allow for examination of the L dependence at fixed (H,K) coordinates. Such measurements indicate intensity that varies only weakly with L (see Supplementary Information), as expected for 2D excitations. This is consistent with recent measurements of a 2D magnetic resonance in FeSe0.4Te0.6 (ref. 21).
All measurements were carried out with the c axis parallel to the incident beam with a sample temperature of 5 (3.5) K for x=0.27 (0.49). a–d, Data from the x=0.27 sample measured using MERLIN with incident energies of 25 (a), 60 (b), 120 (c) and 250 meV (d). e–h, Data from the x=0.49 sample measured using ARCS with incident energies of 40 (e), 60 (f), 120 (g) and 250 meV (h). The x=0.27 (0.49) samples were single crystals with a mass of 16.91 (15.45) g. i–p, Fits to equation (1) convolved with instrumental resolution for the x=0.27 (i–l) and x=0.49 sample (m–p). The fit (i) to the 10 meV data (a) for the x=0.27 sample includes two components rotated by 45∘ in the H–K plane. All other fits include only a single component.
The low-energy magnetic response (Fig. 2a,b) for the x=0.27 sample is characterized by two peaks at wavevectors near (1/2, 1/2). Interestingly, the data do not show four-fold symmetry around this wavevector as expected for the nuclear cell of the P4/n m m space group, but rather form a quartet around the (1, 0) wavevector. With increasing energy, the peaks disperse away from (1/2, 1/2) towards (1, 0) as shown schematically in Fig. 1b. At higher energies, the excitations continue to disperse towards (1, 0) but evolve from spots into rings (Fig. 2c) centred on this wavevector. Eventually, as shown for an energy transfer of 120 meV in Fig. 2d, the excitations evolve into broad spots centred at (1, 0). For the superconducting x=0.49 sample, the low-energy spectrum appears as a series of asymmetric spots (Fig. 2e). However, data measured at a higher energy transfer of 22 meV (Fig. 2f) show separated peaks similar to those in the x=0.27 sample. This can easily be understood by considering that the displacement of these peaks away from (1, 0) is larger in the x=0.49 sample such that the pair of peaks around (1/2, 1/2) have moved closer together and overlap significantly. At an energy of 45 meV (Fig. 2g), the characteristic wavevector appears similar in the two samples but the x=0.49 scattering appears to have not fully evolved into the rings of scattering present in the x=0.27 sample (Fig. 2c). At high energies, the scattering is similar in the two samples, as can be seen by comparing Fig. 2d and h. The excitations persist to energy transfers greater than 250 meV (see Supplementary Information) with Q-dependence similar to that shown at 120 meV for all higher energies.
Examination of the wavevector describing these excitations reveals similarities with the high-TC cuprates. The quartet of peaks is characterized by wavevectors (1±ξ,±ξ) and  that, in square-lattice notation, corresponds to (π±ξ,π) and (π,π±ξ) as shown in Fig. 1b. This is precisely the same wavevector as the low-energy excitations observed in La2−xSrxCuO4 (ref. 9) and YBa2Cu3O6+x (refs 10, 11), indicating remarkable commonality in the excitation spectrum of these two classes of high-TC superconductors. Furthermore, the evolution of the scattering from well-defined peaks at low energies to broadened rings at higher energies is a characteristic property of magnetic excitations in the cuprates23,24. The magnitude of ξ, however, is much larger in Fe1+yTe1−xSex, resulting in low-energy excitations displaced away from (1, 0) and much closer to (1/2, 1/2).
that, in square-lattice notation, corresponds to (π±ξ,π) and (π,π±ξ) as shown in Fig. 1b. This is precisely the same wavevector as the low-energy excitations observed in La2−xSrxCuO4 (ref. 9) and YBa2Cu3O6+x (refs 10, 11), indicating remarkable commonality in the excitation spectrum of these two classes of high-TC superconductors. Furthermore, the evolution of the scattering from well-defined peaks at low energies to broadened rings at higher energies is a characteristic property of magnetic excitations in the cuprates23,24. The magnitude of ξ, however, is much larger in Fe1+yTe1−xSex, resulting in low-energy excitations displaced away from (1, 0) and much closer to (1/2, 1/2).
At low energies, the largest difference between the two concentrations becomes evident as shown in Fig. 3a,b. In addition to the excitations near (1/2, 1/2), an extra component centred near (1/2, 0) is present in the x=0.27 sample (also visible in Fig. 2a). With decreasing energy, the intensity of this component increases, eventually forming the short-range order observed previously for samples with a similar concentration20,25. It has been suggested26 that excess Fe in Te-rich samples results in local moments that may provide a pair-breaking mechanism destroying superconductivity. The component of scattering observed near (1/2, 0) is absent in the x=0.49 sample with no excess Fe (Fig. 3b). Furthermore, the scattering near (1/2, 0) exists inelastically for all energies below ∼10 meV and, as such, exists well below the superconducting gap, potentially providing a pair-breaking mechanism. These observations are consistent with the extra component near (1/2, 0) existing as a result of the influence of extra Fe in the x=0.27 sample.
a,b, Measurements of the x=0.27 (a) and x=0.49 sample (b) were carried out with an incident energy of 25 and 40 meV, respectively. The temperature was 5 (3.5) K for the x=0.27 (0.49) measurements. These data show an extra component in the x=0.27 data centred near (1/2, 0), which is absent in the x=0.49 data. c,d, Fits to equation (1) convolved with instrumental resolution. Fits to the x=0.27 data (c) include two components rotated by 45∘with respect to one another in the H–K plane, whereas fits to the x=0.49 data (d) include only a single, incommensurate component.
To quantify the dispersion of the spin excitations, the data were fitted using the phenomenological Sato–Maki function27 previously used for the cuprates24

where

The form for R(Q) in equation (2) describes excitations four-fold symmetric about (HC,KC)=(1,0). As discussed below, δ parameterizes the dispersion, λ defines the evolution of the spectrum from peaks (large λ) to rings (small λ) and κ is a broadening parameter.
The results of fits to the data presented in Fig. 2a–h using the Sato–Maki function convolved with instrumental resolution are shown in Fig. 2i–l (m–p) for x=0.27 (0.49). The fits agree well with the measurements over the full range of measured energies. The fit quality is also demonstrated in Fig. 4d–g for cuts along  , indicating excellent agreement over a wide range of wavevector and energy transfer. A spin excitation spectrum accurately described by the identical model in both Fe1+yTe1−xSex and the cuprates is further evidence of commonality in these two classes of superconductor. The same Sato–Maki function can be used to describe the extra component in the x=0.27 sample near (1/2, 0) with a rotated R(Q) factor (see Supplementary Information) and the fits shown in Figs 3c and 2i contain both components, again yielding excellent agreement with the data.
, indicating excellent agreement over a wide range of wavevector and energy transfer. A spin excitation spectrum accurately described by the identical model in both Fe1+yTe1−xSex and the cuprates is further evidence of commonality in these two classes of superconductor. The same Sato–Maki function can be used to describe the extra component in the x=0.27 sample near (1/2, 0) with a rotated R(Q) factor (see Supplementary Information) and the fits shown in Figs 3c and 2i contain both components, again yielding excellent agreement with the data.
Data at fixed energies are fitted using equation (1). a, The dispersion along (1+ξ,−ξ) is extracted from the best fit value of δ by noting that  . Below 15 meV, the dispersion was extracted from triple-axis measurements in the (H K0) scattering plane through convolution of equation (1) with instrumental resolution. The dispersion above 15 meV was extracted from time-of-flight data. As instrumental resolution was found to have little effect on the fits to the time-of-flight data, the dispersion was generated without including resolution. For x=0.27, all data analysed were measured at 3.5 K (triple-axis) or 5 K (time-of-flight). For x=0.49, time-of-flight data analysed were measured at 3.5 K, whereas triple-axis data were measured at 20 K to avoid scattering from the magnetic resonance. The horizontal error bars represent the statistical uncertainty in the fit to equation (1), whereas the vertical error bars represent the range of energies included. The solid lines in a are guides to the eye. For clarity, the dispersion is plotted for both positive and negative ξ, noting that equation (1) is an even function of δ. Above 100 meV, the peak position cannot be distinguished from ξ=0. b–e, Cuts at fixed energies obtained by integrating data on either side of the line K=−H over H=±0.1 in the perpendicular (H,H) direction. The data were measured with incident energies of 120 meV (b,d) and 250 meV (c,e). The error bars in b–e represent one sigma and solid lines are fits to equation (1).
. Below 15 meV, the dispersion was extracted from triple-axis measurements in the (H K0) scattering plane through convolution of equation (1) with instrumental resolution. The dispersion above 15 meV was extracted from time-of-flight data. As instrumental resolution was found to have little effect on the fits to the time-of-flight data, the dispersion was generated without including resolution. For x=0.27, all data analysed were measured at 3.5 K (triple-axis) or 5 K (time-of-flight). For x=0.49, time-of-flight data analysed were measured at 3.5 K, whereas triple-axis data were measured at 20 K to avoid scattering from the magnetic resonance. The horizontal error bars represent the statistical uncertainty in the fit to equation (1), whereas the vertical error bars represent the range of energies included. The solid lines in a are guides to the eye. For clarity, the dispersion is plotted for both positive and negative ξ, noting that equation (1) is an even function of δ. Above 100 meV, the peak position cannot be distinguished from ξ=0. b–e, Cuts at fixed energies obtained by integrating data on either side of the line K=−H over H=±0.1 in the perpendicular (H,H) direction. The data were measured with incident energies of 120 meV (b,d) and 250 meV (c,e). The error bars in b–e represent one sigma and solid lines are fits to equation (1).
The best fit value of δ parameterizes the dispersion. If we define the characteristic wavevector as  , then
, then  . The resulting dispersion (Fig. 4a) demonstrates excitations dispersing from a wavevector near (1/2, 1/2) (ξ=−0.5) towards (1, 0) (ξ=0). The shape of the dispersion is reminiscent of the ‘hour glass’ dispersion observed in the cuprates24,28. However, unlike the cuprates, the high-energy excitations of Fe1+yTe1−xSex remain centred near (1, 0) with no evidence for dispersion away from this wavevector. It is important to note that, for both concentrations, the dispersion does not approach the commensurate (1/2, 1/2) wavevector on approaching the elastic condition and, therefore, both samples show an incommensurate excitation spectrum. For energies greater than ∼50 meV, the dispersions are consistent for the two concentrations. However, for lower energies, |ξ| is larger for x=0.49, indicating excitations displaced closer to the (1/2, 1/2) wavevector with larger Se content. This can also be clearly seen in comparing the cuts in Fig. 4b with 4d (25 meV) and 4c with 4e (70 meV). The peaks in the 25 meV data are at clearly different wavevectors, but the distribution of scattering intensity is nearly identical at 70 meV for the two concentrations. It is interesting to note that the sample (x=0.49) with normal-state excitations closer to the resonance wavevector shows bulk superconductivity, whereas only weak superconductivity is observed in the sample with normal-state excitations displaced further from this wavevector.
. The resulting dispersion (Fig. 4a) demonstrates excitations dispersing from a wavevector near (1/2, 1/2) (ξ=−0.5) towards (1, 0) (ξ=0). The shape of the dispersion is reminiscent of the ‘hour glass’ dispersion observed in the cuprates24,28. However, unlike the cuprates, the high-energy excitations of Fe1+yTe1−xSex remain centred near (1, 0) with no evidence for dispersion away from this wavevector. It is important to note that, for both concentrations, the dispersion does not approach the commensurate (1/2, 1/2) wavevector on approaching the elastic condition and, therefore, both samples show an incommensurate excitation spectrum. For energies greater than ∼50 meV, the dispersions are consistent for the two concentrations. However, for lower energies, |ξ| is larger for x=0.49, indicating excitations displaced closer to the (1/2, 1/2) wavevector with larger Se content. This can also be clearly seen in comparing the cuts in Fig. 4b with 4d (25 meV) and 4c with 4e (70 meV). The peaks in the 25 meV data are at clearly different wavevectors, but the distribution of scattering intensity is nearly identical at 70 meV for the two concentrations. It is interesting to note that the sample (x=0.49) with normal-state excitations closer to the resonance wavevector shows bulk superconductivity, whereas only weak superconductivity is observed in the sample with normal-state excitations displaced further from this wavevector.
Finally, we discuss the implications of the observed Q-dependence of the magnetic excitations. As a consequence of the coordination of the chalcogen atoms, the real-space P4/n m m unit cell contains two Fe atoms. On the other hand, as the system is not magnetically ordered, if one considers magnetism primarily associated with the Fe atoms, the effective magnetic unit cell is described by a 2D square lattice. The Brillouin zone of each of these lattices is illustrated in Fig. 1a. As seen in Fig. 2, the observed magnetic scattering shows periodicity compatible with the Fe sublattice Brillouin zone. This is consistent with the periodicity of spin fluctuations observed in the high-TC cuprates, as expected because cuprate magnetism is dominated by Cu atoms that also form a square lattice. The essential magnetism in both Fe1+yTe1−xSex and the cuprates can be captured by the identical model even though the crystal structures themselves have different symmetries. We note that caution is necessary in comparing the Q-dependence of experimental data with theoretical calculations. Some published calculations have been presented in a 2D Brillouin zone based on the P4/n m m lattice. This Brillouin zone is smaller than the square-lattice Brillouin zone and, presented in this manner, calculations fold excitations in the zone centred at (1, 0) back to the zone centred at (0, 0) (ref. 29). This superposes the magnetic response in these two zones, making it difficult to extract the true Q-dependence as measured experimentally. Calculations carried out in the square-lattice Brillouin zone should result in the symmetry of the measured excitation spectrum as confirmed by calculations of the Q-dependent spin susceptibility and gap functions30.
References
Kamihara, Y. et al. Iron-based layered superconductor La[O1−xFx]FeAs (x=0.05–0.12) with TC=26 K. J. Am. Chem. Soc. 130, 3296–3297 (2008).
Chen, X. C. et al. Superconductivity at 43 K in SmFeAsO1−xFx . Nature 453, 761–762 (2008).
Rotter, M., Tegel, M. & Johrendt, D. Superconductivity at 38 K in the iron arsenide (Ba1−xKx)Fe2As2 . Phys. Rev. Lett. 101, 107006 (2008).
Christianson, A. D. et al. Unconventional superconductivity in Ba0.6K0.4Fe2As2 from inelastic neutron scattering. Nature 456, 930–932 (2008).
Lumsden, M. D. et al. Two-dimensional resonant magnetic excitation in BaFe1.84Co0.16As2 . Phys. Rev. Lett. 102, 107005 (2009).
Chi, S. et al. Inelastic neutron-scattering measurements of a three-dimensional spin resonance in the FeAs-based BaFe1.9Ni0.1As2 superconductor. Phys. Rev. Lett. 102, 107006 (2009).
Mook, H. A. et al. Neutron scattering patterns show superconductivity in FeTe0.5Se0.5 likely results from itinerant electron fluctuations. Preprint at <http://arxiv.org/abs/0904.2178v1> (2009).
Ning, F. et al. Spin susceptibility, phase diagram, and quantum criticality in the electron-doped high TC superconductor Ba(Fe1−xCox)2As2 . J. Phys. Soc. Jpn 78, 013711 (2009).
Cheong, S.-W. et al. Incommensurate magnetic fluctuations in La2−xSrxCuO4 . Phys. Rev. Lett. 67, 1791–1794 (1991).
Dai, P., Mook, H. A. & Dogan, F. Incommensurate magnetic fluctuations in YBa2Cu3O6.6 . Phys. Rev. Lett. 80, 1738–1741 (1998).
Mook, H. A. et al. Spin fluctuations in YBa2Cu3O6.6 . Nature 395, 580–582 (1998).
Chen, G. F. et al. Superconductivity at 41 K and its competition with spin-density-wave instability in layered CeO1−xFxFeAs. Phys. Rev. Lett. 100, 247002 (2008).
Ren, Z. et al. Superconductivity at 55 K in iron-based F-doped layered quaternary compound Sm[O1−xFx]FeAs. Chin. Phys. Lett. 25, 2215–2216 (2008).
Wang, X. et al. The superconductivity at 18 K in LiFeAs system. Solid State Commun. 148, 538–540 (2008).
Hsu, F.-C. et al. Superconductivity in the PbO-type structure α-FeSe. Proc. Natl Acad. Sci. USA 105, 14262–14264 (2008).
Yeh, K.-W. et al. Tellurium substitution effect on superconductivity of the α-phase iron selenide. Europhys. Lett. 84, 37002 (2008).
de la Cruz, C. et al. Magnetic order close to superconductivity in the iron-based layered LaO1−xFxFeAs systems. Nature 453, 899–902 (2008).
McGuire, M. A. et al. Phase transitions in LaFeAsO: Structural, magnetic, elastic, and transport properties, heat capacity and Mössbauer spectra. Phys. Rev. B 78, 094517 (2008).
Huang, Q. et al. Neutron-diffraction measurements of magnetic order and a structural transition in the parent BaFe2As2 compound of FeAs-based high-temperature superconductors. Phys. Rev. Lett. 101, 257003 (2008).
Bao, W. et al. Tunable (δπ,δπ)-type antiferromagnetic order in α-Fe(Te, Se) superconductors. Phys. Rev. Lett. 102, 247001 (2009).
Qiu, Y. et al. Spin gap and resonance at the nesting wave vector in superconducting FeSe0.4Te0.6 . Phys. Rev. Lett. 103, 067008 (2009).
Sales, B. C. et al. Bulk superconductivity at 14 K in single crystals of Fe1+yTexSe1−x . Phys. Rev. B 79, 094521 (2009).
Stock, C. et al. From incommensurate to dispersive spin fluctuations: The high energy inelastic spectrum in superconducting YBa2Cu3O6.5 . Phys. Rev. B 71, 024522 (2005).
Vignolle, B. et al. Two energy scales in the spin excitations of the high-temperature superconductor La2−xSrxCuO4 . Nature Phys. 3, 163–167 (2007).
Wen, J. et al. Coexistence and competition of short-range magnetic order and superconductivity in Fe1+δTe1−xSex . Phys. Rev. B 80, 104506 (2009).
Zhang, L., Singh, D. J. & Du, M. H. Density functional study of excess Fe in Fe1+xTe: Magnetism and doping. Phys. Rev. B 79, 012506 (2009).
Sato, H. & Maki, K. Theory of inelastic neutron scattering from Cr and its alloys near the Néel temperature. Int. J. Magn. 6, 183–209 (1974).
Hayden, S. M. et al. The structure of the high-energy spin excitations in a high-transition-temperature superconductor. Nature 429, 531–534 (2004).
Mazin, I. I. et al. Unconventional superconductivity with a sign reversal in the order parameter of LaFeAsO1−xFx . Phys. Rev. Lett. 101, 057003 (2008).
Kuroki, K. et al. Unconventional pairing originating from the disconnected fermi surfaces of superconducting LaFeAsO1−xFx . Phys. Rev. Lett. 101, 087004 (2008).
Acknowledgements
We acknowledge discussions with D. Singh and T. Maier. This work was supported by the Scientific User Facilities Division and the Division of Materials Sciences and Engineering, Office of Basic Energy Sciences, US Department of Energy.
Author information
Authors and Affiliations
Contributions
All authors made critical comments on the manuscript. M.D.L., A.D.C., E.A.G., S.E.N., M.B.S., D.L.A., T.G., G.J.M., C.C. and H.A.M. all contributed to data collection. A.S.S., M.A.M., B.C.S. and D.M. contributed to sample synthesis and characterization.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 794 kb)
Rights and permissions
About this article
Cite this article
Lumsden, M., Christianson, A., Goremychkin, E. et al. Evolution of spin excitations into the superconducting state in FeTe1−xSex. Nature Phys 6, 182–186 (2010). https://doi.org/10.1038/nphys1512
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1512
This article is cited by
-
Nematic fluctuations in an orbital selective superconductor Fe1+yTe1−xSex
Communications Physics (2023)
-
A self-adaptive first-principles approach for magnetic excited states
Quantum Frontiers (2023)
-
Iron pnictides and chalcogenides: a new paradigm for superconductivity
Nature (2022)
-
High-pressure phase diagrams of FeSe1−xTex: correlation between suppressed nematicity and enhanced superconductivity
Nature Communications (2021)
-
Magnetic ground state of FeSe
Nature Communications (2016)