Abstract
Natural and artificially created light fields in three-dimensional space contain lines of zero intensity, known as optical vortices1,2,3. Here, we describe a scheme to create optical beams with isolated optical vortex loops in the forms of knots and links using algebraic topology. The required complex fields with fibred knots and links4 are constructed from abstract functions with braided zeros and the knot function is then embedded in a propagating light beam. We apply a numerical optimization algorithm to increase the contrast in light intensity, enabling us to observe several optical vortex knots. These knotted nodal lines, as singularities of the wave’s phase, determine the topology of the wave field in space, and should have analogues in other three-dimensional wave systems such as superfluids5 and Bose–Einstein condensates6,7.
Similar content being viewed by others
Main
In nature, one never finds the plane waves described in textbooks; real physical waves, such as light beams, are superpositions of many plane waves propagating in different directions. Generically, interference of three or more plane waves results in optical vortex lines, where the intensity is zero, and around which the phase increases by 2π (refs 1, 2). This contrasts with a single plane wave, for which the intensity is uniform, and the wavefronts—the surfaces of constant phase—are nested planes perpendicular to the wavevector k. The presence of vortices disrupts this regular arrangement of wavefronts3: a straight vortex line parallel to k has helicoidal wavefronts; a circular vortex loop perpendicular to k is the edge of a punctured wavefront. The situation is more complicated when a single, isolated vortex loop is knotted8. Here, we establish theoretically and demonstrate experimentally that waves may contain a single isolated knotted vortex loop.
The global topology of such a knotted vortex field is non-trivial. Wavefront surfaces with all phase labels must intersect on the vortex lines in any optical field, and fill all space. If the vortex line is knotted, all wavefront surfaces have a knotted boundary curve, and are thus multiply connected. Although the vortices occupy a finite volume of space, this topology affects the entire wave field. Such non-trivial topology of physical fields arises elsewhere in physics, such as flows in fluid dynamics9 (including Lord Kelvin’s vortex atom hypothesis10), quantum condensates6,7 and field theory11,12. Time-dependent solutions of Maxwell’s equations in which all electric field lines have the form of torus knots (knots that can be drawn, without crossing, on a torus) were found in ref. 13. This knotting of light complements our present approach, in which the topology resides in the optical complex amplitude, giving knots that are directly observable in the intensity distribution of the beam. Knotted vortex loops are hypothesized to be generic in turbulent and chaotic wave fields, including superfluids5, optical14 and biological waves15, although only unknotted linked vortex rings have been identified in large-scale simulations of these systems. In mathematical topology, the complex scalar wavefunctions we describe are fibred knots4. As such, they contrast with optical beams studied previously16,17, in which the vortex knots and links were of necessity threaded by infinite vortex lines, and so have no underlying wavefront topology of interest, and were only torus knots.
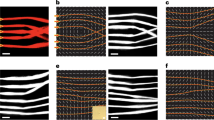
In knot theory, complex-valued scalar functions of three-dimensional (3D) space with knotted zero lines are found as polynomial expansions around singularities in high-dimensional spaces, called Milnor maps18. This approach, originally restricted to a class of cable knots4 (including the torus knots), was subsequently extended19,20 to include other fibred knots including the figure-8 knot. We mathematically realize these knotted and linked zeroes by devising complex functions in an abstract 3D space with zero lines on a periodic braid, reminiscent of the constructions of refs 19, 20. Examples of two such braids, described in detail below, are shown in Fig. 1a,b, enclosed in a cylinder. This cylinder and its interior are then smoothly mapped to the solid torus, with height coordinate h mapping to the torus azimuth φ. Under this transformation, the braid becomes one or more closed rings, with the topology of a knot or link, localized in three dimensions. The thrice-twisted double helix of Fig. 1a is mapped to a trefoil knot (Fig. 1c), and the pigtail braid in Fig. 1b, the figure-8 knot of Fig. 1d. The construction of such Milnor maps f(r), for r=(x,y,z), is described explicitly in the following paragraph.
a, A two-strand braid is twisted three times, represented by equation (1) with n=3. b, A three-strand pigtail braid represented by equation (2), made from two copies of the basic braid crossing sequence (n=2). Each strand follows a  -shaped trajectory (in black) in the horizontal plane. c, Nodal trefoil knot arising from the Milnor map of the braid in a. The toroidal tube around the knot is the image of the cylinder around the original braid, and the strands are coloured the same way. d, Figure-8 knot arising from the pigtail braid in a similar way. e, Trefoil knotted nodal line arising from propagating the Milnor polynomial of c in the z=0 plane. The phase in this plane is represented by the coloured disc (with the scale in Fig. 2). f, Figure-8 knot in a propagating field, arising in a similar way from the Milnor polynomial for d.
-shaped trajectory (in black) in the horizontal plane. c, Nodal trefoil knot arising from the Milnor map of the braid in a. The toroidal tube around the knot is the image of the cylinder around the original braid, and the strands are coloured the same way. d, Figure-8 knot arising from the pigtail braid in a similar way. e, Trefoil knotted nodal line arising from propagating the Milnor polynomial of c in the z=0 plane. The phase in this plane is represented by the coloured disc (with the scale in Fig. 2). f, Figure-8 knot in a propagating field, arising in a similar way from the Milnor polynomial for d.
A periodic N-strand braid may be represented by N distinct points in the complex plane, sj(h), trigonometrically parameterized by height h, with sj(h+2π)=sj(h), j=1,…,N. For each h, these points are the roots of a polynomial in the variable u,

The roots corresponding to the helical braid in Fig. 1a execute a circular trajectory as h varies, and those of the pigtail braid in Fig. 1b, a lemniscate. On replacing h with v=exp(i h), ph(u) may be rewritten as a complex polynomial q(u,v) in complex variables u and v. The braids of Fig. 1a,b correspond to the polynomials


n is the number of repeats of the basic braid crossing sequence (denoted by the yellow arrow in the figure): n=3 for Fig. 1a, n=2 for Fig. 1b. The two crossings that occur in the braid in Fig. 1b occur with different signs because the polynomial in equation (2) involves both v and its complex conjugate v*. Making u and v functions of position r=(x,y,z) in 3D space,

defines the Milnor map f(r)=q(u(r),v(r)), which has knotted and linked zero lines determined by the underlying braid. For qhelix(u,v) the procedure gives a (2,n) torus knot (such as the trefoil knot in Fig. 1c) and for qpigtail(u,v), a family of knots4,19 including the figure-8 knot (n=2, Fig. 1d), Borromean rings (n=3) and the Turk’s head knot 818 (n=4). The numerator of f(r) is a polynomial in x,y,z, which we call the Milnor polynomial. The functions in equation (3) are the standard complex coordinates for the 3-sphere.
Such complex fields can generate physical wave fields with knotted vortex lines. Many optical fields ψ satisfy the paraxial equation

Mathematically, there is a unique paraxial wave field ψ, which satisfies equation (4), and that exactly coincides with any given Milnor polynomial in the plane z=0. For many explicit examples we have studied, this field, on evolution in z, has the same nodal line topology as the Milnor map f(r). Cases this works for include those described above for n<10; however, the knot of the Milnor map of u5−v2 and that of its corresponding paraxial polynomial do not agree, and we lack a general proof of why this construction works in the cases it does. The knotted nodal lines for propagating trefoil and figure-8 knot fields are shown in Fig. 1e,f. A description of the various functions we use for the trefoil knot is given explicitly in the Supplementary Information. This procedure of constructing polynomial solutions coinciding with the Milnor polynomial when z=0, and containing the same knots, also works for other linear wave equations, such as the Helmholtz equation, with appropriate choice of parameters.
Although such propagating polynomials satisfy equation (4), they do not represent physical beams, as they diverge as  . However, the knot remains when the polynomial in the z=0 plane is multiplied by a Gaussian profile of width w,exp(−(x2+y2)/2w2), provided w is sufficiently large (typically w>1). As the width w decreases, other vortex lines approach the knot from
. However, the knot remains when the polynomial in the z=0 plane is multiplied by a Gaussian profile of width w,exp(−(x2+y2)/2w2), provided w is sufficiently large (typically w>1). As the width w decreases, other vortex lines approach the knot from  , and eventually reconnect with the knotted or linked vortices21, destroying the topology. These extra vortices arise from interference on propagation between the different z-dependent Gouy phases22,23 of the propagating Gaussian optical modes into which the Gaussian-modulated polynomials naturally decompose. Beams of this form in the focal plane are easy to manipulate experimentally, and we do so as superpositions of the Laguerre–Gauss basis modes22, labelled by (l,p). The azimuthal index is represented by l and p is the radial index of the mode. This analytic approach to Gaussian beam propagation can be taken with any mode set, such as Hermite–Gaussian modes23.
, and eventually reconnect with the knotted or linked vortices21, destroying the topology. These extra vortices arise from interference on propagation between the different z-dependent Gouy phases22,23 of the propagating Gaussian optical modes into which the Gaussian-modulated polynomials naturally decompose. Beams of this form in the focal plane are easy to manipulate experimentally, and we do so as superpositions of the Laguerre–Gauss basis modes22, labelled by (l,p). The azimuthal index is represented by l and p is the radial index of the mode. This analytic approach to Gaussian beam propagation can be taken with any mode set, such as Hermite–Gaussian modes23.
The exact positions of vortex lines are susceptible to experimental imperfections, and such complicated destructive interference structures are hard to realize in the laboratory. Our experiment is based on a diffractive holographic scheme, in which a Gaussian laser beam is synthesized with the desired phase and intensity in its focal plane. This is done by a spatial light modulator (SLM), which is a computer-controlled liquid-crystal device that imprints phase patterns on laser light. We configure a single SLM as a diffractive component with a spatially dependent blazing function. The light propagating from the hologram has a phase pattern determined by the shape of the grating lines on the hologram, and intensity determined by their contrast24.
Such techniques are frequently used in sculpting the bright patterns in light beams for applications such as optical trapping25. Various algorithms can be used to determine an optimized beam profile, by converging on the desired pattern by means of a cost function that depends on the resulting 2D or 3D pattern26. Such optimization minimizes the effects of experimental imperfections, such as optical misalignment and pixellation in the SLM. Vortices, which are found in low-intensity regions of the light, are particularly sensitive to experimental noise, and optimization is required for experimental realization.
To optimize our knot field profile for experiments, we have developed an algorithm to shape darkness. First, we choose a sufficiently large width w to avoid risk of reconnection with vortex lines approaching from high z. This beam is decomposed into Laguerre–Gauss modes, giving a finite set of coefficients. We then iteratively optimize the superposition by randomly changing the coefficients. Only changes that maintain the vortex topology in a prescribed cylindrical volume around the original knot are considered further (numerically implemented by requiring the x y-projected knot to have the same planar representation27), forbidding the approach of any extra vortices owing to the Gaussian factor. The change is kept if the value of the cost function is lower than that of the unchanged superposition. This cost function is defined by  , where I0 is a saturating intensity (set at a few per cent of Imax).
, where I0 is a saturating intensity (set at a few per cent of Imax).
The constraint of fixed vortex topology forces an unusual restriction on the cost-function landscape, which nevertheless seems robust: for each knot, several runs of a few hundred steps converge to the same set of coefficients. An illustration of the difference between the vortex trefoil knot in a Gaussian beam, before and after optimization, is shown in Fig. 2. The net result of the algorithm is to separate the vortex points in each cross-section with regions of higher intensity, and to tend to align the axial vortex line segments with the propagation direction.
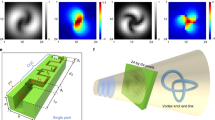
a–f, Several plots for the trefoil knot, emphasizing the difference between the unoptimized and optimized Laguerre–Gauss superpositions for width w=1.2: intensity in the waist plane (z=0) (unoptimized (a), optimized (b)), phase in the same plane (c,d, respectively) and three-dimensional vortex knot on propagation (e,f). In e,f, the black lines give the transverse Gaussian width w, and the length of the yellow line in the propagation direction represents a Rayleigh range. For the chosen width w=1.2, the unoptimized (optimized) coefficients weighting the Laguerre–Gauss modes (l, p) in these plots are: (0, 0) 1.71 (1.51); (0, 1) −5.66 (−5.06); (0, 2) 6.38 (7.23); (0, 3) −2.30 (−2.03); (3, 0) −4.36 (−3.97), normalized so that the sums of the squares are equal to 100. As the superposition consists of only one Laguerre–Gauss mode with non-zero azimuthal index l, the superposition retains three-fold symmetry on propagation.
We have used the outputs of this algorithm to create isolated optical vortex knots in laser light using a SLM. A CCD (charge-coupled device) array mounted on a motorized stage28 images the field interferometrically. Thus, the phase at each point is measured directly29, allowing precise location of the positions of the intersection of the vortex lines with the measurement plane. About 100 such planes are measured, allowing the vortex configuration in the volume to be determined precisely. Figure 3 shows three experimentally measured configurations: the Hopf link (generated with unoptimized coefficients), the trefoil knot and the cinquefoil knot ((2, 5) torus knot). These are based on different n in qhelix(u,v) in equation (1) (n=2, 3 and 5), corresponding to the number of repeats of the double-helix crossing of Fig. 1a. Movies of the trefoil and cinquefoil knot structures, and the sequence of measured phase maps from which these vortex knots were reconstructed, are given in the Supplementary Information. We have been unable to generate experimental knots based on the pigtail braid of Fig. 1b with sufficient contrast to be observed experimentally, so the vortices observed in our experiments are all torus knots.
The curves represent optical vortex lines, numerically reconstructed from measured optical phase fields at different propagation distances. These knots were all generated with the polynomial qhelix(u,v) of equation (1), with different n, and optimized with different widths w. a, Hopf link (n=2, w=1.4, coefficients weighting the Laguerre–Gauss mode (l, p): (0, 0) 2.63; (0, 1) −6.32; (0, 2) 4.21; (2, 0) −5.95). b, Trefoil knot (n=3, w=1.2, coefficients as given for the optimized case in Fig. 2). c, Cinquefoil knot (n=5, w=0.93, coefficients (0, 0) 0.61; (0, 1) −2.56; (0, 2) 6.15; (0, 3) −6.35; (0, 4) 2.92; (0, 5) −0.61; (5, 0) −2.45). The black and yellow arrows are as in Fig. 2.
We have described and implemented a scheme to create isolated optical vortex knots and links in propagating laser fields. Our approach combines holographic optimization with an abstract algebraic representation of knotted complex fields, although experimental realization has not been possible for all of the knotted fields we find theoretically. The new technique of holographically optimizing dark fields complements the more familiar shaping of bright regions of beams. This technique may find application in the design of optical landscapes for blue-detuned trapping6 or super-resolved fluorescent imaging30, both of which require precision shaping of nodal structures. The fact that the z=0 sections of Milnor polynomials evolve topologically to give fibred knots raises the intriguing possibility of understanding initial-value problems through knot theory: the non-trivial 3D topological information is encrypted in the 2D section taken as the hologram. It is unknown whether other physical waves, satisfying for instance nonlinear wave equations, will have the same topological propagation properties.
References
Nye, J. F. Natural Focusing and Fine Structure of Light (IoPP, 1999).
Dennis, M. R., O’Holleran, K. & Padgett, M. J. Singular optics: Optical vortices and polarization singularities. Prog. Opt. 53, 293–363 (2009).
Nye, J. F. & Berry, M. V. Dislocations in wave trains. Proc. R. Soc. A 336, 165–190 (1974).
Rolfsen, D. Knots and Links (AMS, 2003).
Poole, D. R., Scoffield, H., Barenghi, C. F. & Samuels, D. C. Geometry and topology of superfluid turbulence. J. Low Temp. Phys. 132, 97–117 (2003).
Matthews, M. R. et al. Vortices in a Bose–Einstein condensate. Phys. Rev. Lett. 83, 2498–2501 (1999).
Ruostekoski, J. & Dutton, Z. Engineering vortex rings and systems for controlled studies of vortex interactions in Bose–Einstein condensates. Phys. Rev. A 72, 063626 (2005).
Winfree, A. T., Winfree, E. M. & Seifert, H. Organizing centers in a cellular excitable medium. Physica D 17, 109–115 (1985).
Moffatt, H. K. Degree of knottedness of tangled vortex lines. J. Fluid Mech. 35, 117–129 (1969).
Thompson, W. (Lord Kelvin) On vortex atoms. Phil. Mag. 34, 15–24 (1867).
Faddeev, L. & Niemi, A. J. Stable knot-like structures in classical field theory. Nature 387, 58–61 (1997).
Battye, R. A. & Sutcliffe, P. M. Knots as stable soliton solutions in a three-dimensional classical field theory. Phys. Rev. Lett. 81, 4798–4801 (1998).
Irvine, W. T. M. & Bouwmeester, D. Linked and knotted beams of light. Nature Phys. 4, 716–720 (2008).
O’Holleran, K., Dennis, M. R. & Padgett, M. J. Topology of light’s darkness. Phys. Rev. Lett. 102, 143902 (2009).
Winfree, A. T. Persistent tangled vortex rings in generic excitable media. Nature 371, 233–236 (1994).
Berry, M. V. & Dennis, M. R. Knotted and linked phase singularities in monochromatic waves. Proc. R. Soc. A 457, 2251–2263 (2001).
Leach, J., Dennis, M. R., Courtial, J. & Padgett, M. J. Knotted threads of darkness. Nature 432, 165 (2004).
Milnor, J. Singular Points of Complex Hypersurfaces (Princeton Univ. Press, 1969).
Perron, B. Le noeud huit est algebrique réel. Inv. Math. 65, 441–451 (1982).
Rudolph, L. Isolated critical points of mappings from R4 to R2 and a natural splitting of the Milnor number of a classical fibered link. Part I: Basic theory; examples. Comment. Math. Helv. 62, 630–645 (1987).
Berry, M. V. & Dennis, M. R. Topological events on wave dislocation lines: Birth and death of small loops, and reconnection. J. Phys. A 40, 65–74 (2007).
Siegman, A. E. Lasers (Univ. Science Books, 1986).
Freund, I. Saddle point wave fields. Opt. Commun. 163, 230–242 (1999).
Leach, J., Dennis, M. R., Courtial, J. & Padgett, M. J. Vortex knots in light. New J. Phys. 7, 55 (2005).
Grier, D. G. A revolution in optical manipulation. Nature 424, 810–816 (2003).
Whyte, G. & Courtial, J. Experimental demonstration of holographic three-dimensional light shaping using a Gerchberg–Saxton algorithm. New J. Phys. 7, 117 (2005).
Ewing, B. & Millett, K. C. in The Mathematical Heritage of C F Gauss (ed. Rassias, G. M.) 225–266 (World Scientific, 1991).
O’Holleran, K., Dennis, M. R., Flossmann, F. & Padgett, M. J. Fractality of light’s darkness. Phys. Rev. Lett. 100, 053902 (2008).
O’Holleran, K., Flossmann, F., Dennis, M. R. & Padgett, M. J. Methodology for imaging the 3D structure of singularities in scalar and vector optical fields. J. Opt. A: Pure Appl. Opt. 11, 094020 (2009).
Westphal, V. & Hell, S. W. Nanoscale resolution in the focal plane of an optical microscope. Phys. Rev. Lett. 94, 143903 (2005).
Acknowledgements
This work was supported by the Leverhulme Trust. M.R.D. is a Royal Society University Research Fellow.
Author information
Authors and Affiliations
Contributions
M.R.D. and R.P.K. developed the knot construction on the basis of an idea of M.R.D. M.J.P. and K.O. developed the optimization algorithms and designed the experiment. B.J. and K.O. carried out the experiment. R.P.K. was responsible for the representation of results. M.R.D. prepared the manuscript with support from M.J.P.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 214 kb)
Supplementary Movie
Supplementary Movie 1 (MOV 2667 kb)
Supplementary Movie
Supplementary Movie 2 (MOV 2559 kb)
Supplementary Movie
Supplementary Movie 3 (MOV 473 kb)
Supplementary Movie
Supplementary Movie 4 (MOV 492 kb)
Rights and permissions
About this article
Cite this article
Dennis, M., King, R., Jack, B. et al. Isolated optical vortex knots. Nature Phys 6, 118–121 (2010). https://doi.org/10.1038/nphys1504
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1504
This article is cited by
-
Topological atom optics and beyond with knotted quantum wavefunctions
Communications Physics (2024)
-
Effects of aberrations on 3D optical topologies
Communications Physics (2023)
-
Coupled quantum vortex kinematics and Berry curvature in real space
Communications Physics (2023)
-
Scalar optical hopfions
eLight (2022)
-
Optical excitations of Skyrmions, knotted solitons, and defects in atoms
Communications Physics (2022)