Abstract
Experiments on single nitrogen–vacancy (N–V) centres in diamond, which include electron spin resonance1, Rabi oscillations2, single-shot spin readout3 and two-qubit operations with a nearby13C nuclear spin4, show the potential of this spin system for solid-state quantum information processing. Moreover, N–V centre ensembles can have spin-coherence times exceeding 50 μs at room temperature5. We have developed an angle-resolved magneto-photoluminescence microscope apparatus to investigate the anisotropic electron-spin interactions of single N–V centres at room temperature. We observe negative peaks in the photoluminescence as a function of both magnetic-field magnitude and angle that are explained by coherent spin precession and anisotropic relaxation at spin-level anti-crossings. In addition, precise field alignment unmasks the resonant coupling to neighbouring ‘dark’ nitrogen spins, otherwise undetected by photoluminescence. These results demonstrate the capability of our spectroscopic technique for measuring small numbers of dark spins by means of a single bright spin under ambient conditions.
Similar content being viewed by others
Main
The N–V defect pair, with trigonal symmetry6, has an anisotropic electron-spin hamiltonian owing to spin–spin and spin–orbit interactions7. Consequently, the degrees of spin-level mixing and coupling to nearby impurity spins are very sensitive to the orientation of an applied magnetic field, which has not been controlled in experiments on single N–V centres. Figure 1a depicts the atomic structure and relevant energy levels of the (negatively charged) N–V centre. The triplet (3A) ground state8,9,10 has a zero-field splitting between the |mS=0〉 and |mS=±1〉 spin sublevels, where mS is the quantum number of the spin sublevel, quantized along the N–V symmetry axis, a 〈111〉 crystal axis11. Zero-field spin splittings have also been measured in the triplet (3E) excited state but there is no consensus on the arrangement of sublevels12,13,14,15. Linearly polarized optical excitation of the 3A→3E transition preferentially pumps the spin system into the |0〉 ground-state sublevel16. In addition, the average photon-emission rate is substantially smaller for transitions involving the |±1〉 levels than for the |0〉 level3, which enables the spin state to be determined by the photoluminescence intensity IPL. Both of the latter two effects have been attributed to spin-dependent intersystem crossing to the singlet (1A) level11,17.
a, The atomic structure and relevant energy levels. The green ‘bond’ depicts the N–V symmetry axis. b, The spatial image of IPL on a linear colour scale, showing the emission from several N–V centres; NV1–NV4 (left to right) are marked. c, The intensity correlation function g(2)(τ) versus τ for NV1, indicating single photon emission. d, Optically detected ESR for NV1. IPL versus microwave frequency νMW (circles) with a lorentzian fit (solid line). The laser power is 1 mW for b and 370 μW for c and d.
The single-crystal samples investigated here are commercially available (Sumitomo Electric Industries) high-temperature high-pressure diamond with two polished parallel (100) surfaces and nominal dimensions of 1.4 mm×1.4 mm×1.0 mm. They contain nitrogen impurities with densities of 1019–1020 cm−3, measured by ultraviolet absorption18. N–V centres are naturally present with substantially lower densities ranging from 1010 to 1013 cm−3. For ensemble measurements, samples are irradiated with 1.7-MeV electrons with a dose of 5×1017 cm−3 and subsequently annealed at 900 ∘C for 2 h to increase the N–V centre concentration6.
The phonon-broadened 3E→3A transition of the N–V centre is detected by means of non-resonant photoluminescence microscopy (see Methods). For example, Fig. 1b is a spatial image of the spectrally integrated photoluminescence from a diamond sample with the laser focused roughly 1 μm below the surface. Multiple resolution-limited features are observed in the 20 μm×20 μm field. In order to determine that a given feature is due to a single emitter, a histogram is plotted of the time τ between consecutive photon detection events using a Hanbury Brown and Twiss detection geometry19, yielding the experimental intensity correlation function g(2)(τ). Figure 1c shows the data from a colour centre labelled NV1. The value of g(2)(0) is below 0.5, proving that NV1 is a single-colour centre20. In addition, the rise of g(2)(τ) above unity with increasing |τ| is indicative of intersystem crossing to the 1A metastable state20,21.
These single-photon emitters are further characterized by optically detected electron spin resonance (ESR; see Methods). Figure 1d contains data from NV1 with zero applied magnetic field. In this case, the |±1〉 ground-state levels are degenerate so that only one resonance (mS=0→±1) is observed at 2.87 GHz, the characteristic zero-field splitting of N–V centres11. The data are fit with a lorentzian of 11 MHz full-width at half-maximum (solid line), which is comparable to reported values in similar diamond samples1.
Strain-dependent optical measurements on ensembles of N–V centres have indicated that electric dipole transitions are allowed for dipoles in the plane perpendicular to the symmetry axis6. Figure 2a depicts an N–V centre with transition dipoles  and
and  in a (111) plane. The excitation is along [001] for all measurements, therefore IPL depends on the laser polarization angle φ owing to unequal excitation of the two dipoles. The dependence of IPL on φ is measured for 20 N–V centres and shows either vertical or horizontal lobes, as exemplified for three N–V centres in Fig. 2b. The measured anisotropies, defined as the ratio IPL(φ=0∘)/IPL (φ=90∘), are roughly 2:1 and 1:2 on average; a simple anisotropy calculation gives 3:1, 3:1, 1:3 and 1:3 for the N–V symmetry axis along [111],
in a (111) plane. The excitation is along [001] for all measurements, therefore IPL depends on the laser polarization angle φ owing to unequal excitation of the two dipoles. The dependence of IPL on φ is measured for 20 N–V centres and shows either vertical or horizontal lobes, as exemplified for three N–V centres in Fig. 2b. The measured anisotropies, defined as the ratio IPL(φ=0∘)/IPL (φ=90∘), are roughly 2:1 and 1:2 on average; a simple anisotropy calculation gives 3:1, 3:1, 1:3 and 1:3 for the N–V symmetry axis along [111],  ,
,  and
and  , respectively (see Methods). The measured data are modified by the presence of polarized background photoluminescence (subtracted from the data) and a small dip, most visible for NV2 at φ=0∘, which varies in depth from centre to centre. Nevertheless, comparison of the measured and calculated anisotropies enables the number of possible orientations of a given centre to be reduced from four to two.
, respectively (see Methods). The measured data are modified by the presence of polarized background photoluminescence (subtracted from the data) and a small dip, most visible for NV2 at φ=0∘, which varies in depth from centre to centre. Nevertheless, comparison of the measured and calculated anisotropies enables the number of possible orientations of a given centre to be reduced from four to two.
a, Measurement geometry indicating transition dipoles X and Y. b, Normalized IPL (radial axis) versus the laser polarization angle φ for NV1, NV2 and NV3. Polarization along  corresponds to φ=0∘ and data at φ and φ+180∘ are identical. c, Upper panel: calculated ground-state spin splitting ν as a function of B for θ=6∘ (solid lines) and 54.7∘ (dashed lines). Middle panel: overlap |α|2 of each spin level with |0〉z at the same two angles. Lower panel: IPL versus B for NV1, NV2 and NV3, with ∼1∘ angle between B and [111]. The laser power is 370 μW for b and 1 mW for c.
corresponds to φ=0∘ and data at φ and φ+180∘ are identical. c, Upper panel: calculated ground-state spin splitting ν as a function of B for θ=6∘ (solid lines) and 54.7∘ (dashed lines). Middle panel: overlap |α|2 of each spin level with |0〉z at the same two angles. Lower panel: IPL versus B for NV1, NV2 and NV3, with ∼1∘ angle between B and [111]. The laser power is 370 μW for b and 1 mW for c.
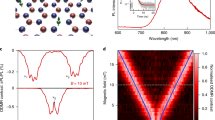
The double degeneracy of the polarization anisotropy is lifted by application of a magnetic field B. The upper panel of Fig. 2c shows the ground-state spin levels as a function of B (the amplitude of B) calculated using the hamiltonian7 H=gμBB · S+D(Sz2−S(S+1)/3), where μB is the Bohr magneton, g=2.00 is the electron g-factor, S is the total electron spin with magnitude S=1 and D=2.88 GHz is the ground-state spin splitting. A level anti-crossing (LAC) near 1,000 G is predicted for an N–V centre with symmetry axis at a small angle to B (6∘; solid lines), but not for a large angle (54.7∘; dashed lines). The middle panel shows |α|2, the overlap of |0〉z with each spin level, |mS〉=α|0〉z+β|−1〉z+γ|+1〉z, where |β|2 and |γ|2 are the other respective overlaps and the subscript z denotes the [111] basis; the evolution of |α|2 with B, calculated for both angles, illustrates the mixing of spin states and will be relevant in modelling the data. The lower panel is a plot of IPL as a function of B, with an angle of ∼1∘ between B and [111], for the same three N–V centres as in Fig. 2b. Whereas NV1 and NV2 have similar polarization dependences, their field dependences show that the symmetry axis of NV1 (NV2) is (non-)parallel to B. For NV1, the negative peak at ∼1,000 G coincides with the calculated LAC. In addition, NV1 shows a peak at ∼500 G, the origin of which is less clear.
In order to investigate these peaks further, IPL is measured as a function of B with B at a series of angles θ in the  plane; a selection of such data from NV1 is shown in Fig. 3a. As B approaches the [111] direction (θ→0∘), the LAC peak narrows, as expected from ensemble measurements22,23. At sufficiently small angles, however, the LAC peak amplitude decreases for NV1 (Fig. 3b) or even vanishes for some centres, such as NV4 (Fig. 3c). This is in contrast to the ensemble measurements22,23 that showed a maximum in the LAC peak amplitude at θ=0∘. According to the hamiltonian above, however, spin mixing should vanish at θ=0∘. The presence of residual spin mixing at θ=0∘ has been attributed to strain and nuclear interactions24, which vary from centre to centre.
plane; a selection of such data from NV1 is shown in Fig. 3a. As B approaches the [111] direction (θ→0∘), the LAC peak narrows, as expected from ensemble measurements22,23. At sufficiently small angles, however, the LAC peak amplitude decreases for NV1 (Fig. 3b) or even vanishes for some centres, such as NV4 (Fig. 3c). This is in contrast to the ensemble measurements22,23 that showed a maximum in the LAC peak amplitude at θ=0∘. According to the hamiltonian above, however, spin mixing should vanish at θ=0∘. The presence of residual spin mixing at θ=0∘ has been attributed to strain and nuclear interactions24, which vary from centre to centre.
a, IPL versus B for NV1 at specified magnetic-field angles θ. b, Zoom of data in a (points) with fits (lines) to model described in the text. Data for θ=0∘ are taken with smaller field steps and fit with an angle of 0.2∘ to account for residual spin mixing (see the text). c, IPL versus B for NV4 (points) and fits (lines) at specified field angles. d, Normalized amplitudes A (points) of LAC and 500-G peaks versus θ with fits (lines). Laser power is 1 mW for NV1 and 2.9 mW for NV4.
The LAC can be modelled for small values of θ by considering |0〉 and |−1〉 as pseudo-spin-1/2 states. With preferential population of |0〉z, the |+1〉 level is ignored because it has a negligible overlap with |0〉z (see Fig. 2c, middle panel). We then have an effective hamiltonian H=gμB(B−B0)· s, where B0 accounts for the zero-field spin splitting and s is the pseudo-spin operator. The Bloch equations for B in the  plane are taken to be
plane are taken to be

where  , ħ is the reduced Planck constant,
, ħ is the reduced Planck constant,  is the Larmor precession vector,
is the Larmor precession vector,  ,
,  , B0∥z∥[111],Γ is the rate of optical spin orientation along z, and T1 and T2 are effective spin relaxation times that depend on Γ (see Methods). In this model, the spin relaxation is anisotropic in that T1 and T2 are fixed relative to the crystal axes rather than the magnetic field. The steady-state solution for sz is
, B0∥z∥[111],Γ is the rate of optical spin orientation along z, and T1 and T2 are effective spin relaxation times that depend on Γ (see Methods). In this model, the spin relaxation is anisotropic in that T1 and T2 are fixed relative to the crystal axes rather than the magnetic field. The steady-state solution for sz is

We then take IPL=an0+bn−1=a(1/2+sz)+b(1/2−sz), where a and b (n0 and n−1) are the photoluminescence rates (occupation probabilities) for the |0〉z and |−1〉z levels, respectively. This simple model describes the experimental data for a wide range of angles and magnetic fields, where the same fit parameters are used for all angles (Fig. 3b,c lines). The fits yield T1=64 ns and T2=11 ns for NV4 using a laser power of 2.9 mW (Fig. 3c) and T1=130 ns and T2=23 ns for a power of 900 μW (not shown). The results indicate that the laser introduces substantial anisotropic spin relaxation by means of excitation out of the ground-state manifold. This source of decoherence can be mitigated through pulsed excitation4.
The 500-G peak evolves similarly to the LAC peak but over a broader angular range. It has nearly the same amplitude and width at a given field angle for all N–V centres investigated with suitable orientation. In addition, the peak has been observed in all four samples measured. The evolution of the 500-G peak with θ and B can be reasonably accounted for in the model by postulating an LAC in the excited state, as is expected to occur at some field owing to the presence of zero-field spin splittings12,13,14. Figure 3d shows the normalized amplitudes A of the 500-G and LAC (1,000-G) peaks as a function of θ. Fits of the model to this data (red lines) and to the field scans (fits not shown) yield T1=36 ns and T2=1.8 ns for an excited-state LAC at ∼500 G.
Similar data are taken on ensembles of N–V centres in Fig. 4a, where the 500-G peak is found to reduce in amplitude by ∼50% at θ=0∘. In addition, higher-resolution field scans around 500 G (Fig. 4a, inset) show a quintuplet of peaks characteristic of the hyperfine structure of substitutional nitrogen (NS) centres25. These peaks appear when the magnetic field tunes the electron spin splitting of N–V centres into resonance with the many surrounding NS centres, resulting in enhanced cross-relaxation by means of the magnetic dipole interaction26,27,28. Notably, the NS peak amplitudes diminish as |θ| increases, suggesting that the 500-G peak is associated with a decrease in spin polarization, like the LAC peak.
a, IPL versus B for an ensemble of N–V centres at two field angles. Inset: higher-resolution scans around 500 G showing the nitrogen hyperfine structure. b, A single N–V centre (NV4) coupling to several nitrogen centres. IPL versus B at two indicated field angles with 300 μW laser power. c, IPL versus B at two indicated laser powers for NV1, showing broadening of nitrogen peaks with increased power. For a (inset), b and c, a small linear background is subtracted from the data.
The above results point to a regime (|θ|<1∘) where the depolarizing effects of the 500-G peak are mitigated, showing the coupling of a single N–V centre to its neighbouring NS spins. Figure 4b shows two field scans of IPL for NV4 at θ=0∘ and 1∘; the NS resonances become visible with a sufficiently small angle between B and [111]. Figure 4c shows similar data for NV1 at θ=0∘ with powers of 300 and 900 μW; the NS peaks broaden and diminish in relative magnitude at higher power, possibly resulting from ionization of the NS centres29. The depths of the NS peaks, differing for NV4 and NV1, are sensitive to the particular spatial distribution of nearby nitrogen spins.
Finally, it is worth noting that the NS centres are ‘dark’ in that they are not directly detected by photoluminescence. By measuring a single N–V centre, the number of NS spins that can be probed is decreased by orders of magnitude relative to the ensemble measurements. Furthermore, this dark-spin spectroscopy technique is in principle applicable to a variety of paramagnetic defects in diamond. With higher purity samples and single-ion implantation30, these results could make possible the long-range coupling of two individually addressable N–V centres connected by a chain of dark spins, enabling experimental tests of spin-lattice theories and quantum information processing schemes.
Methods
Experimental techniques
The measurement apparatus is based on a confocal microscope with a Hanbury Brown and Twiss detection scheme19. A diode-pumped solid-state laser emitting at 532 nm is linearly polarized and focused onto the sample with a microscope objective of numerical aperture 0.73 and working distance 4.7 mm. The linear polarization is set to any desired angle by changing the retardance of a variable wave plate (fast axis at 45∘ to the initially vertical polarization) followed by a quarter-wave plate (fast axis vertical). The laser spot is positioned on the sample in both lateral dimensions with a fast steering mirror. The photoluminescence from the sample is collected by the same microscope objective, passed through a dichroic mirror and a 640-nm long-pass filter, and sent through a 50/50 beam-splitter to two fibre-coupled silicon avalanche photodiode modules.
For antibunching measurements, the outputs of the detectors are connected to a time-correlated single-photon counting module. The data are normalized by the detector count rates, time bin width and total integration time to yield g(2)(τ). The data are not corrected for background photoluminescence. For measurements of N–V centre ensembles, photoluminescence is detected with a photodiode and lock-in amplifier. In general, the photoluminescence is used as a feedback signal to compensate for thermal drift, enabling a single N–V centre to be tracked for several days. The samples are at room temperature for all measurements discussed in this letter.
The static magnetic field B is applied to the sample with a permanent magnet mounted on a multiaxis stage that allows the distance between the magnet and the sample to be adjusted by a stepper motor, thereby setting B at the sample. In addition, the polar and azimuthal angles of B are manually adjustable with micrometers while keeping B constant at the sample to better than 1%. For ESR measurements, a 25-μm-diameter gold wire is connected to a microwave signal generator (with 16 dB m power output) and placed in close proximity (∼50 μm) to the laser spot.
Polarization anisotropy calculation
According to Fermi’s golden rule in the electric dipole approximation, the absorption rate is proportional to |D · E|2, where D is the dipole matrix element and E is the excitation electric-field vector. The absorption anisotropy is estimated to be |Y · V|2/|X · H|2, where X and Y are the dipoles (see Fig. 2a) and  and H∥[110] are polarization vectors. A more accurate calculation would account for the dipole radiation pattern, the large numerical aperture of the microscope objective and refraction at the diamond–air boundary. However, the simple equation above is sufficient to explain both the anisotropy orientations and degeneracies that are measured.
and H∥[110] are polarization vectors. A more accurate calculation would account for the dipole radiation pattern, the large numerical aperture of the microscope objective and refraction at the diamond–air boundary. However, the simple equation above is sufficient to explain both the anisotropy orientations and degeneracies that are measured.
Bloch equation simplifications
Equation (1) has been simplified by defining effective relaxation times T1 and T2 that depend on Γ. Explicitly, (T1)−1=(Tz)−1+2Γ, where Tz is the intrinsic relaxation time of sz. Likewise, T2 has a similar form. As Γ is proportional to the laser power, the equation above explains why T1 and T2 decrease with increasing power, as observed in the experiments.
References
Gruber, A. et al. Scanning confocal optical microscopy and magnetic resonance on single defect centers. Science 276, 2012–2014 (1997).
Jelezko, F., Gaebel, T., Popa, I., Gruber, A. & Wrachtrup, J. Observation of coherent oscillations in a single electron spin. Phys. Rev. Lett. 92, 076401 (2004).
Jelezko, F. et al. Single spin states in a defect center resolved by optical spectroscopy. Appl. Phys. Lett. 81, 2160–2162 (2002).
Jelezko, F. et al. Observation of coherent oscillation of a single nuclear spin and realization of a two-qubit conditional quantum gate. Phys. Rev. Lett. 93, 130501 (2004).
Kennedy, T. A., Colton, J. S., Butler, J. E., Linares, R. C. & Doering, P. J. Long coherence times at 300 K for nitrogen-vacancy center spins in diamond grown by chemical vapor deposition. Appl. Phys. Lett. 83, 4190–4192 (2003).
Davies, G. & Hamer, M. F. Optical studies of the 1.945 eV vibronic band in diamond. Proc. R. Soc. A 348, 285–298 (1976).
Pryce, M. H. L. A modified perturbation procedure for a problem in paramagnetism. Proc. Phys. Soc. A 63, 25–29 (1950).
Reddy, N. R. S., Manson, N. B. & Krausz, E. R. Two-laser spectral hole burning in a colour centre in diamond. J. Lumin. 38, 46–47 (1987).
van Oort, E., Manson, N. B. & Glasbeek, M. Optically detected spin coherence of the diamond N-V centre in its triplet ground state. J. Phys. C 21, 4385–4391 (1988).
Redman, D. A., Brown, S., Sands, R. H. & Rand, S. C. Spin dynamics and electronic states of N-V centers in diamond by EPR and four-wave-mixing spectroscopy. Phys. Rev. Lett. 67, 3420–3423 (1991).
Loubser, J. H. N. & van Wyk, J. A. Electron spin resonance in the study of diamond. Rep. Prog. Phys. 41, 1201–1248 (1978).
Redman, D., Brown, S. & Rand, S. C. Origin of persistent hole burning of N-V centers in diamond. J. Opt. Soc. Am. B 9, 768–774 (1992).
Manson, N. B. & Wei, C. Transient hole-burning in N-V centre in diamond. J. Lumin. 58, 158–160 (1994).
Lenef, A. et al. Electronic structure of the N-V center in diamond: experiments. Phys. Rev. B 53, 13427–13440 (1996).
Martin, J. P. D. Fine structure of excited3E state in nitrogen-vacancy centre of diamond. J. Lumin. 81, 237–247 (1999).
Harrison, J., Sellars, M. J. & Manson, N. B. Optical spin polarization of the N-V centre in diamond. J. Lumin. 107, 245–248 (2004).
Nizovtsev, A. P. et al. NV centers in diamond: spin-selective photokinetics, optical ground state spin alignment and hole burning. Physica B 340–342, 106–110 (2003).
Kaiser, W. & Bond, W. L. Nitrogen, a major impurity in common type I diamond. Phys. Rev. 115, 857–863 (1959).
Hanbury Brown, R. & Twiss, R. Q. Correlation between photons in two coherent beams of light. Nature 177, 27–29 (1956).
Kurtsiefer, C., Mayer, S., Zarda, P. & Weinfurter, H. Stable solid-state source of single photons. Phys. Rev. Lett. 85, 290–293 (2000).
Beveratos, A., Brouri, R., Poizat, J.-P. & Grangier, P. in Quantum Communication, Computing and Measurement 3 (eds Tombesi, P. & Hirota, O.) 261–267 (Kluwer Academic/Plenum, New York, 2001).
van Oort, E. & Glasbeek, M. Fluorescence detected level-anticrossing and spin coherence of a localized triplet state in diamond. Chem. Phys. 152, 365–373 (1991).
Martin, J. P. D. et al. Spectral hole burning and Raman heterodyne signals associated with an avoided crossing in the NV centre in diamond. J. Lumin. 86, 355–362 (2000).
He, X. -F., Manson, N. B. & Fisk, P. T. H. Paramagnetic resonance of photoexcited N-V defects in diamond. I. Level anticrossing in the3A ground state. Phys. Rev. B 47, 8809–8815 (1993).
Smith, W. V., Sorokin, P. P., Gelles, I. L. & Lasher, G. J. Electron spin resonance of nitrogen donors in diamond. Phys. Rev. 115, 1546–1552 (1959).
Holliday, K., Manson, N. B., Glasbeek, M. & van Oort, E. Optical hole-bleaching by level anti-crossing and cross relaxation in the N-V centre in diamond. J. Phys. C 1, 7093–7102 (1989).
van Oort, E. & Glasbeek, M. Cross-relaxation dynamics of optically excited N-V centers in diamond. Phys. Rev. B 40, 6509–6517 (1989).
van Oort, E., Stroomer, P. & Glasbeek, M. Low-field optically detected magnetic resonance of a coupled triplet-doublet defect pair in diamond. Phys. Rev. B 42, 8605–8608 (1990).
Farrer, R. G. On the substitutional nitrogen donor in diamond. Solid State Commun. 7, 685–688 (1969).
Meijer, J. et al. Generation of single colour centers by focussed nitrogen implantation. Preprint at http://arxiv.org/abs/cond-mat/0505063 (2005).
Acknowledgements
We thank O. Gywat for valuable discussions and G. C. Farlow for high-energy electron irradiation of several samples. This work was supported by AFOSR, DARPA/MARCO and ARO.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Epstein, R., Mendoza, F., Kato, Y. et al. Anisotropic interactions of a single spin and dark-spin spectroscopy in diamond. Nature Phys 1, 94–98 (2005). https://doi.org/10.1038/nphys141
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys141
This article is cited by
-
Field programmable spin arrays for scalable quantum repeaters
Nature Communications (2023)
-
Thermal-activated escape of the bistable magnetic states in 2D Fe3GeTe2 near the critical point
Communications Physics (2023)
-
Experimental demonstration of adversarial examples in learning topological phases
Nature Communications (2022)
-
Excited-state spin-resonance spectroscopy of V\({}_{{{{{{{{\rm{B}}}}}}}}}^{-}\) defect centers in hexagonal boron nitride
Nature Communications (2022)
-
Manifestation in IR-Luminescence of Cross Relaxation Processes between NV-Centers in Weak Magnetic Fields
Journal of Applied Spectroscopy (2022)