Abstract
Angle-resolved photoemission spectroscopy (ARPES) probes the momentum-space electronic structure of materials and provides invaluable information about the high-temperature superconducting cuprates1. Likewise, scanning tunnelling spectroscopy (STS) reveals the cuprates’ real-space inhomogeneous electronic structure. Recently, researchers using STS have exploited quasiparticle interference (QPI)—wave-like electrons that scatter off impurities to produce periodic interference patterns—to infer properties of the quasiparticles in momentum space. Surprisingly, some interference peaks in Bi2Sr2CaCu2O8+δ (Bi-2212) are absent beyond the antiferromagnetic zone boundary, implying the dominance of a particular scattering process2. Here, we show that ARPES detects no evidence of quasiparticle extinction: quasiparticle-like peaks are measured everywhere on the Fermi surface, evolving smoothly across the antiferromagnetic zone boundary. This apparent contradiction stems from differences in the nature of single-particle (ARPES) and two-particle (STS) processes underlying these probes. Using a simple model, we demonstrate extinction of QPI without implying the loss of quasiparticles beyond the antiferromagnetic zone boundary.
Similar content being viewed by others
Main
Recently, STS has been used to infer momentum-space information from the Fourier transform of the position (r)- and energy (ω)-dependent local density of states (LDOS), ρ(r,ω) (refs 3, 4, 5, 6). Conventionally, a superconductor has well-defined momentum eigenstates (that is, Bogoliubov quasiparticles), so ρ(r,ω) is spatially homogeneous. However, scattering from inhomogeneities often present in the cuprates7 mixes momentum eigenstates and QPI manifests itself as a spatial modulation of ρ(r,ω) with well-defined wave vector q, appearing in the Fourier transform, ρ(q,ω). QPI experiments are interpreted using the octet model3,4,5,6, positing that wave vectors q1−7 connecting the ends of ‘banana shaped’ contours of constant energy (CCEs) dominate ρ(q,ω). Dispersing wave vectors are associated with coherent superconducting quasiparticles and the evolution of q1−7 as a function of bias voltage is used to infer the Fermi surface and the magnitude of the d-wave superconducting gap. QPI experiments have found that the intensity of some of the peaks in ρ(q,ω) vanishes on approaching the diagonal line between (0,π) and (π,0) (corresponding to the antiferromagnetic zone boundary)5. These results lead naturally to speculation about the disappearance of QPI and possible extinction of quasiparticles themselves near the boundary of the Brillouin zone (antinodal region).
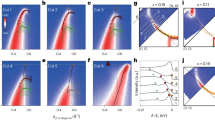
Notably, ARPES has long shown antinodal quasiparticles below the critical temperature Tc in Bi-2212 over a wide doping range (p>0.08; refs 8, 9, 10), although this point has not been a focus in the literature. In Fig. 1, we report data on single crystals of Bi-2212 at four dopings spanning much of the same doping range as reported in recent STS studies5, from slightly underdoped (Tc=92 K, denoted UD92) to substantially underdoped (UD50). ARPES measurements were carried out at Beamline 5–4 of the Stanford Synchrotron Radiation Lightsource using a Scienta R4000 electron analyser. Samples were cleaved in situ at a pressure better than 5×10−11 torr and measured at 10 K with an energy resolution of 8 meV. UD50 was measured with 19-eV photons with cuts parallel to Γ Y and the other samples were measured with 22.7-eV photons with cuts parallel to Γ M. These data demonstrate sharp peaks at low binding energy, associated with coherent quasiparticles, in all of the energy distribution curves (EDCs) around the Fermi surface, strongly arguing against extinction in the single-particle spectrum. On the other hand, Fourier-transform STS studies report dispersing QPI over only a limited energy range, corresponding to the region of the Fermi surface intermediate between the node and the antinode. In this energy range, both ARPES and Fourier-transform STS show a similar Fermi surface for samples with p∼11% (Fig. 1f), but quasiparticles are clear in ARPES both in the nodal region and in the antinodal region, the latter being the focus of our study. Although the antinode is associated with pseudogap physics, antinodal quasiparticles seem to ‘know’ about superconductivity: for underdoped Bi-2212, the antinodal quasiparticle weight has been shown to scale with the superfluid density2,8 and Tc. The inset of Fig. 1f illustrates that the quasiparticle peak emerges near the antinode only below Tc (ref. 11), whereas the antinodal gap seems to smoothly evolve into the pseudogap above Tc.
a–d, EDCs at kF: node (top) to antinode (bottom). Insets: Fermi surface intersection for each cut. e, Octet model QPI wave vectors, q1–q7, connect the ends of CCEs (red solid lines)5 around the Fermi surface (dashed line), where blue (yellow) regions represent Δ(k)>0 (Δ(k)<0). f, Fourier-transform (FT) STS infers the Fermi surface by tracking dispersing QPI wave vectors, terminating at the antiferromagnetic zone boundary (dashed line)5. For a similar doping, ARPES detects quasiparticles extending to the antinode. Inset: UD75 EDCs at the antinode measured at 85 K and 65 K, showing emergence of the quasiparticle peak near Tc.
The EDCs in Fig. 1 were fitted to a simple model to assess whether there is anomalous scattering near the antiferromagnetic zone boundary. Although many factors contribute to the amplitude and width of the quasiparticle peaks, including matrix element and kz effects12, qualitative conclusions about the single-particle scattering rate can be deduced by analysing the momentum dependence of the peak width. Symmetrized EDCs were fitted to a spectral function with an energy-dependent scattering rate, Γ(ω)=α ω, convolved with the experimental energy resolution. A similar model was found to provide a robust fit for the spatially inhomogeneous STS conductances seen in Bi-2212 (ref. 13). At k=kF, the only free parameters are the prefactor, α, and the gap energy, Δ(k); together, these define a characteristic scattering rate, Γ2*(k)=α Δ(k). Figure 2 shows Γ2* as a function of Fermi surface angle for UD75 and UD92, plotted together with the fitted gap. Near the antinode, the peak width is smaller than the gap, implying that the peaks are quasiparticle-like in this region of interest. For UD92, the quasiparticle width changes little from the node to the antinode, a result similar to earlier work on overdoped samples14. The UD75 scattering rate shows a stronger momentum dependence, but the overall variation is still only a factor of three. For both dopings, there is no anomaly in the scattering at the antiferromagnetic zone boundary, ruling out proposals for quasiparticle extinction that invoke a sudden increase in single-particle scattering there5.
a,b, Symmetrized EDCs at kF for UD75 (a) and UD92 (b) were fitted to an energy-dependent scattering rate, Γ=α ω, convolved with the experimental energy resolution. The characteristic scattering rate, Γ2*=α Δ(k), is plotted as a function of Fermi surface angle along with the fitted Δ(k). Error bars for Γ2* are estimated by the 3σ confidence interval of the fitting and error bars for the gap are described in ref. 10. There is no evidence that the scattering rate diverges near the antiferromagnetic zone boundary for either doping. In addition, the peak width in the antinodal region is smaller than the gap, indicating that the peaks are quasiparticle-like.
What could plausibly explain the apparent contradiction between ARPES and Fourier-transform STS results? One intriguing observation is that not all QPI wave vectors in ρ(q,ω) vanish across the antiferromagnetic zone boundary: q1,4,5 survive, whereas the others fall below the Fourier-transform STS noise floor5. Here, we study the effects of quasiparticle scattering from impurities on the basis of a weak-coupling approach15. Although this neglects the large, relevant, spatial inhomogeneity in the LDOS shown with STS (ref. 7), it places a simple focus on the differences between measurements, contrasting electron removal spectra in ARPES against two-particle QPI mechanisms in Fourier-transform STS.
On the basis of ARPES results, the electron propagators are described by the Nambu Green’s function  in the superconducting state and the momentum-dependent
in the superconducting state and the momentum-dependent  matrix determines the non-uniform part of ρ(q,ω) (ref. 16):
matrix determines the non-uniform part of ρ(q,ω) (ref. 16):

where  is written in terms of Pauli matrices
is written in terms of Pauli matrices  , the unit matrix
, the unit matrix  , the band structure ξ(p) and the d-wave superconducting gap Δ(p)=Δ0[cos (pxa)−cos(pya)]/2. Contributions to the
, the band structure ξ(p) and the d-wave superconducting gap Δ(p)=Δ0[cos (pxa)−cos(pya)]/2. Contributions to the  matrix can be classified according to how they modify electron parameters: conventional impurity scattering occurs in the
matrix can be classified according to how they modify electron parameters: conventional impurity scattering occurs in the  channel, whereas local superconducting gap modification occurs in the
channel, whereas local superconducting gap modification occurs in the  channel.
channel.
A single impurity at site (0, 0) locally modifies hopping and the d-wave superconducting gap through an impurity contribution to the Hamiltonian17,18,19:  , where spin indices have been suppressed. The hopping and d-wave gap modulations, δ t(r) and δΔ(r), are proportional to δ(r−a x)±δ(r−a y)+δ(r+a x)±δ(r+a y), where a is the square lattice spacing and the upper (lower) sign is for hopping (d-wave gap) modulation. Given this form of the impurity Hamiltonian, the Fourier transform,
, where spin indices have been suppressed. The hopping and d-wave gap modulations, δ t(r) and δΔ(r), are proportional to δ(r−a x)±δ(r−a y)+δ(r+a x)±δ(r+a y), where a is the square lattice spacing and the upper (lower) sign is for hopping (d-wave gap) modulation. Given this form of the impurity Hamiltonian, the Fourier transform,  , has a simple momentum-space form:
, has a simple momentum-space form:  for hopping and d-wave gap modulated scattering, respectively. In the
for hopping and d-wave gap modulated scattering, respectively. In the  channel (gap modulation), scattering vanishes between points with opposite order-parameter phases. Thus, q2,3,6,7 vanish identically, whereas q1,4,5 persist. In the
channel (gap modulation), scattering vanishes between points with opposite order-parameter phases. Thus, q2,3,6,7 vanish identically, whereas q1,4,5 persist. In the  channel (hopping modulation), scattering between equivalent points leads to no such cancellation, but the momentum dependence of the
channel (hopping modulation), scattering between equivalent points leads to no such cancellation, but the momentum dependence of the  matrix implies a loss of intensity for q vectors connecting points p and p+q, which both lie on the antiferromagnetic zone boundary. Thus, the disappearance of QPI peaks associated with q2,3,6,7 at the antiferromagnetic zone boundary for the types of disorder considered here may be associated simply with the momentum dependence of the
matrix implies a loss of intensity for q vectors connecting points p and p+q, which both lie on the antiferromagnetic zone boundary. Thus, the disappearance of QPI peaks associated with q2,3,6,7 at the antiferromagnetic zone boundary for the types of disorder considered here may be associated simply with the momentum dependence of the  matrix, rather than implying the ‘extinction’ of quasiparticles. This also may reconcile the observation that the QPI peaks vanish even at large dopings (p≈0.19), a regime with diminished influence from the antiferromagnetic Mott insulating state.
matrix, rather than implying the ‘extinction’ of quasiparticles. This also may reconcile the observation that the QPI peaks vanish even at large dopings (p≈0.19), a regime with diminished influence from the antiferromagnetic Mott insulating state.
The analysis presented above—a single impurity scatterer embedded in an infinite host—provides a simple view of the momentum dependence of the  matrix and a plausible explanation for the loss of QPI peak intensity at the antiferromagnetic zone boundary. However, it cannot generally describe the behaviour of Fourier-transform STS QPI peak intensity as a function of bias voltage or the implications associated with the Fourier transform of the Z map, a ratio of the LDOS at positive and negative bias, rather than the LDOS itself. A better comparison with Fourier-transform STS results from considering the effects of an extended ‘patch’ impurity embedded in a finite-size, periodic host with the
matrix and a plausible explanation for the loss of QPI peak intensity at the antiferromagnetic zone boundary. However, it cannot generally describe the behaviour of Fourier-transform STS QPI peak intensity as a function of bias voltage or the implications associated with the Fourier transform of the Z map, a ratio of the LDOS at positive and negative bias, rather than the LDOS itself. A better comparison with Fourier-transform STS results from considering the effects of an extended ‘patch’ impurity embedded in a finite-size, periodic host with the  matrix determined self-consistently. Finite-size effects are partially mitigated by smoothing the impurity with a Gaussian envelope, thus decreasing the influence of the impurity on electronic parameters further from the centre of the patch. In addition, the QPI intensity is determined from a Fourier transform of the Z map, as done in Fourier-transform STS experiments4,5. More details of the calculation including the exact patch geometry and modulation parameters can be found in the Supplementary Information.
matrix determined self-consistently. Finite-size effects are partially mitigated by smoothing the impurity with a Gaussian envelope, thus decreasing the influence of the impurity on electronic parameters further from the centre of the patch. In addition, the QPI intensity is determined from a Fourier transform of the Z map, as done in Fourier-transform STS experiments4,5. More details of the calculation including the exact patch geometry and modulation parameters can be found in the Supplementary Information.
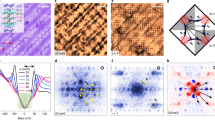
Figure 3c–h shows results for 5%, 10% and 15% hole doping. The dashed line in each panel indicates the energy associated with the antiferromagnetic zone boundary. Note that the general trends agree with the initial analysis from a single impurity scatterer. Intensities for peaks q2,3,6,7, shown in Fig. 3c,e,g, initially rise on moving away from the nodal point and then begin to fall on approaching the antiferromagnetic zone boundary. The intensity for QPI peaks q1,5 is small initially and rises abruptly as the bias voltage approaches and crosses the energy associated with the antiferromagnetic zone boundary, both trends in agreement with the single impurity analysis. This behaviour is in qualitative agreement with the experimental intensity profiles as a function of energy for all QPI peaks5. Although there are general quantitative changes with band-structure parameters, impurity ‘patch’ size and shape and degree of modulation, the qualitative agreement with the single-impurity analysis and experimental findings remains robust.
a, Sketch of the patch used for calculations. b, Z map for |ω/Δ0|=0.15. The QPI wave vectors q1−q7 are indicated. c–h, QPI peak intensities determined from the Z map for 5% (c,d), 10%(e,f) and 15% (g,h) hole doping. c,e and g show the intensity for wave vectors q7, q2,6 and q3. The dashed line in each panel indicates the energy where the tips of the CCEs cross the antiferromagnetic zone boundary, where the peak intensities associated with q2,3,6,7 vanish. d,f and h show the intensities for wave vectors q1 and q5, which rise on approaching the antiferromagnetic zone boundary.
References
Damascelli, A., Hussain, Z. & Shen, Z.-X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473–541 (2003).
Ding, H. et al. Coherent quasiparticle weight and its connection to high-Tc superconductivity from angle-resolved photoemission. Phys. Rev. Lett. 87, 227001 (2001).
McElroy, K. et al. Relating atomic-scale electronic phenomena to wave-like quasiparticle states in superconducting Bi2Sr2CaCu2O8+δ . Nature 422, 592–596 (2003).
Hanaguri, T. et al. Quasiparticle interference and superconducting gap in Ca2−xNaxCuO2Cl2 . Nature Phys. 3, 865–871 (2007).
Kohsaka, Y. et al. How Cooper pairs vanish approaching the Mott insulator in Bi2Sr2CaCu2O8+δ . Nature 454, 1072–1078 (2008).
McElroy, K. et al. Coincidence of checkerboard charge order and antinodal state decoherence in strongly underdoped superconducting Bi2Sr2CaCu2O8+δ . Phys. Rev. Lett. 94, 197005 (2005).
Lang, K. M. et al. Imaging the granular structure of high-Tc superconductivity in underdoped Bi2Sr2CaCu2O8+δ . Nature 415, 412–416 (2002).
Feng, D. L. et al. Signature of superfluid density in the single-particle excitation spectrum of Bi2Sr2CaCu2O8+δ . Science 289, 277–281 (2000).
Tanaka, K. et al. Distinct Fermi-momentum-dependent energy gaps in deeply underdoped Bi2212. Science 314, 1910–1913 (2006).
Lee, W. S. et al. Abrupt onset of a second energy gap at the superconducting transition of underdoped Bi2212. Nature 450, 81–84 (2007).
Sato, T. et al. Low energy excitation and scaling in Bi2Sr2Can−1CunO2n+4 (n=1–3): Angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 89, 067005 (2002).
Bansil, A., Lindroos, M., Sahrakorpi, S. & Markiewicz, R. S. Influence of the third dimension of quasi-two-dimensional cuprate superconductors on angle-resolved photoemission spectra. Phys. Rev. B 71, 012503 (2005).
Alldredge, J. W. et al. Evolution of the electronic excitation spectrum with strongly diminishing hole density in superconducting Bi2Sr2CaCu2O8+δ . Nature Phys. 4, 319–326 (2008).
Bogdanov, P. V. et al. Anomalous momentum dependence of the quasiparticle scattering rate in overdoped Bi2Sr2CaCu2O8 . Phys. Rev. Lett. 89, 167002 (2002).
Fang, A. C. et al. Gap-inhomogeneity-induced electronic states in superconducting Bi2Sr2CaCu2O8+δ . Phys. Rev. Lett. 96, 017007 (2006).
Kampf, A. P. & Devereaux, T. P. Extended impurity potential in a d x2−y2 superconductor. Phys. Rev. B 56, 2360–2363 (1997).
Zhu, J. X. Dopant-induced local pairing inhomogeneity in Bi2Sr2CaCu2O8+δ. Preprint at <http://arxiv.org/abs/cond-mat/0508646> (2005).
Nunner, T. S., Chen, W., Andersen, B. M., Melikyan, A. & Hirschfeld, P. J. Fourier transform spectroscopy of d-wave quasiparticles in the presence of atomic scale pairing disorder. Phys. Rev. B 73, 104511 (2006).
Johnston, S., Vernay, F. & Devereaux, T. P. Impact of an oxygen dopant in Bi2Sr2CaCu2O8+δ . Europhys. Lett. 86, 37007 (2009).
Acknowledgements
We thank N. Nagaosa and J. Zaanen for helpful discussions. SSRL is operated by the US Department of Energy, Office of Basic Energy Science, Division of Chemical Science and Material Science. This work is supported by the US Department of Energy, Office of Science, Division of Materials Science, with contracts DE-AC02-76SF00515, DE-FG03-01ER45929-A001 and NSF grant DMR-0604701.
Author information
Authors and Affiliations
Contributions
I.M.V. analysed ARPES data and wrote the portions of the manuscript and Supplementary Information relevant to ARPES results. W.-S.L. carried out ARPES experiments on samples grown by T.S. and K.T. carried out experiments on samples grown by T.F. B.M. and E.A.N. wrote and modified the computer codes and carried out the computational simulations. T.P.D., B.M. and E.A.N. wrote and edited those portions of the main text and Supplementary Information relevant to the simulations. T.P.D. and Z.-X.S. are responsible for project direction, planning and infrastructure.
Corresponding author
Supplementary information
Supplementary Information
Supplementary Information (PDF 1059 kb)
Rights and permissions
About this article
Cite this article
Vishik, I., Nowadnick, E., Lee, W. et al. A momentum-dependent perspective on quasiparticle interference in Bi2Sr2CaCu2O8+δ. Nature Phys 5, 718–721 (2009). https://doi.org/10.1038/nphys1375
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1375
This article is cited by
-
Particle–hole asymmetric superconducting coherence peaks in overdoped cuprates
Nature Physics (2022)
-
Direct comparison of ARPES, STM, and quantum oscillation data for band structure determination in Sr2RhO4
npj Quantum Materials (2020)
-
ARPES Autocorrelation in Electron-Doped Cuprate Superconductors
Journal of Superconductivity and Novel Magnetism (2020)
-
Holographic maps of quasiparticle interference
Nature Physics (2016)
-
In situ carrier tuning in high temperature superconductor Bi2Sr2CaCu2O8+ by potassium deposition
Science Bulletin (2016)