Abstract
The strongest adversary in quantum information science is decoherence, which arises owing to the coupling of a system with its environment1. The induced dissipation tends to destroy and wash out the interesting quantum effects that give rise to the power of quantum computation2, cryptography2 and simulation3. Whereas such a statement is true for many forms of dissipation, we show here that dissipation can also have exactly the opposite effect: it can be a fully fledged resource for universal quantum computation without any coherent dynamics needed to complement it. The coupling to the environment drives the system to a steady state where the outcome of the computation is encoded. In a similar vein, we show that dissipation can be used to engineer a large variety of strongly correlated states in steady state, including all stabilizer codes, matrix product states4, and their generalization to higher dimensions5.
Similar content being viewed by others
Main
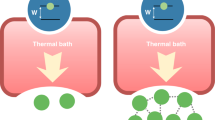
The situation we have in mind is shown in Fig. 1. A quantum system composed of N particles (such as qubits) is organized in space according to a particular geometry (in the figure, a one-dimensional lattice). Neighbouring systems are coupled to some local environments, which are dissipative in nature and tend to drive the system to a steady state. Our idea is to engineer those couplings, so that the environments drive the system to a desired final state. The coupling to the environment will be static, so that the desired state is obtained after some time without having to actively control the system. Note that the role of the environments is to dissipate (or, more precisely, evacuate) the entropy of the system, and by choosing the couplings appropriately we can use this effect to drive our system.
We will show first how to design the interactions with the environment to implement universal quantum computation. This new method, which we refer to as dissipative quantum computation (DQC), defies some of the standard criteria for quantum computation because it requires neither state preparation, nor unitary dynamics6. However, it is nevertheless as powerful as standard quantum computation. Then we will show that dissipation can be engineered7 to prepare ground states of frustration-free Hamiltonians. Those include matrix product states4,8,9 (MPSs) and projected entangled pair states5,9 (PEPSs), such as graph states10 and Kitaev11 and Levin–Wen12 topological codes. Both DQC and dissipative state engineering (DSE) are robust in the sense that, given the dissipative nature of the process, the system is driven towards its steady state independent of the initial state and hence of eventual perturbations along the way.
Here, we will concentrate first on DQC, showing how given any quantum circuit one can construct a locally acting master equation for which the steady state is unique, encodes the outcome of the circuit and is reached in polynomial time (with respect to the one corresponding to the circuit). Then we will show how to construct dissipative processes that drive the system to the ground state of any frustration-free Hamiltonian. In the Methods section, we will prove that MPS (ref. 9) and certain kinds of PEPS (ref. 9) can be efficiently prepared using this method, and in Supplementary Information we will give details of the proofs. In this letter we will not consider specific physical set-ups where our ideas can be implemented. Nevertheless, the Methods section will provide a universal way of engineering the master equations required for DQC and DSE, which can be easily adapted to current experiments 13 based on, for example, atoms in optical lattices 14 or trapped ions15. Thus, we expect that our predictions may be experimentally tested in the near future.
Let us start with DQC by considering N qubits in a line and a quantum circuit specified by a sequence of nearest-neighbour qubit operations {Ut}t=1T. We define  , so that |ψT〉 is the final state after the computation. Our goal is to find a master equation
, so that |ψT〉 is the final state after the computation. Our goal is to find a master equation  with a Liouvillian in Lindblad form16
with a Liouvillian in Lindblad form16

where the Lkacts locally and has a steady state, ρ0: (1) that is unique; (2) that can be reached in a time poly(T); (3) such that ψT can be extracted from it in a time poly(T). As in Feynman’s construction of a quantum simulator3, we consider another auxiliary register with states {|t〉}t=0T, which will represent the time. We choose the Lindblad operators


where i=1,…,N and t=0,…,T. It is clear that the L terms act locally except for the interaction with the extra register, which can be made local as well. Furthermore,

is a steady state, that is,  . Given such a state, the result of the actual quantum computation can be read out with probability 1/T by measuring the time register. In Supplementary Information, we show that ρ0 is the unique steady state and that the Liouvillian has a spectral gap Δ=π2/(2T+3)2. This means indeed that the steady state will be reached in polynomial time in T. Note that this gap is independent of N as well as of the actual quantum computation that is carried out (that is, independent of the Ut). It is also shown that the same gap is retained if the clock register is encoded in the unary way proposed by Kitaev and co-workers17, making the Lindblad operators strictly local. A sketch of the proof is as follows. First, we do a similarity transformation on
. Given such a state, the result of the actual quantum computation can be read out with probability 1/T by measuring the time register. In Supplementary Information, we show that ρ0 is the unique steady state and that the Liouvillian has a spectral gap Δ=π2/(2T+3)2. This means indeed that the steady state will be reached in polynomial time in T. Note that this gap is independent of N as well as of the actual quantum computation that is carried out (that is, independent of the Ut). It is also shown that the same gap is retained if the clock register is encoded in the unary way proposed by Kitaev and co-workers17, making the Lindblad operators strictly local. A sketch of the proof is as follows. First, we do a similarity transformation on  that replaces all gates Ui with the identity gates, showing that its spectrum is independent of the actual quantum computation. Second, another similarity transformation is done that makes
that replaces all gates Ui with the identity gates, showing that its spectrum is independent of the actual quantum computation. Second, another similarity transformation is done that makes  Hermitian and block-diagonal. Each block can then be diagonalized exactly leading to the claimed gap.
Hermitian and block-diagonal. Each block can then be diagonalized exactly leading to the claimed gap.
In some sense, the present formalism can be seen as a robust way of doing adiabatic quantum computation18 (errors do not accumulate and the path does not have to be engineered carefully) and implementing quantum random walks19, and it might therefore be easier to tackle interesting open questions, such as the quantum probabilistically-checkable-proofs theorem, in this setting20. In addition, it seems that the dissipative way of preparing ground states is more natural than to use adiabatic time evolution, as nature itself prepares them by cooling.
Let us now turn to DSE and consider again a quantum system with N particles on a lattice in any dimension. We are interested in ground states Ψ, of Hamiltonians

that are frustration-free, meaning that Ψ minimizes the energy of each Hλ individually, and local in the sense that Hλ acts non-trivially only on a small set  of sites (for example, nearest neighbours). We can assume the terms Hλ to be projectors and we will denote the orthogonal projectors by Pλ=1−Hλ. States Ψ of the considered form are, for example, all PEPS (including MPS and stabilizer states21).
of sites (for example, nearest neighbours). We can assume the terms Hλ to be projectors and we will denote the orthogonal projectors by Pλ=1−Hλ. States Ψ of the considered form are, for example, all PEPS (including MPS and stabilizer states21).
We will consider discrete time evolution generated by a trace-preserving completely positive map instead of a master equation. These two approaches are basically equivalent22 as every local completely positive map  can be associated with a local Liouvillian through
can be associated with a local Liouvillian through  , which leads to the same fixed points and spectrum. We choose completely positive maps of the form
, which leads to the same fixed points and spectrum. We choose completely positive maps of the form

where the pλterms are probabilities and Uλ,1,…,Uλ,m is a set of unitaries acting non-trivially only within region λ. They effectively rotate part of the high-energy space (with support of Hλ) to the zero-energy space, so that  increases. As for Liouvillians (1), we could similarly take Lλ,i=UiHλ, or the ones associated with the completely positive map.
increases. As for Liouvillians (1), we could similarly take Lλ,i=UiHλ, or the ones associated with the completely positive map.
We show now that for every frustration-free Hamiltonian, the completely positive map in equation (2) converges to the ground-state space if we choose the unitaries Uλ,i to be completely depolarizing, that is,  . For ease of notation, we will explain the proof for the case of a one-dimensional ring with nearest-neighbour interactions labelled by the first site λ=1,…,N. Assume ρ is such that its expectation value with respect to the projector Ψ onto the ground-state space of H is non-increasing under applications of
. For ease of notation, we will explain the proof for the case of a one-dimensional ring with nearest-neighbour interactions labelled by the first site λ=1,…,N. Assume ρ is such that its expectation value with respect to the projector Ψ onto the ground-state space of H is non-increasing under applications of  , that is, in particular
, that is, in particular  . Expressing this in the Heisenberg picture in which
. Expressing this in the Heisenberg picture in which  , we get
, we get

where the first inequality comes from discarding (positive) terms in the sum and the second one is due to bounding all partial traces of Hλ from below by the respective smallest eigenvalue ν. Note that the latter is strictly positive unless H has a product state as the ground state (in which case the statement becomes trivial). Hence, we must have tr[ρ H]=0; that is, ρ is a ground state of H. It is easily seen that the same argument applies for more general interactions on arbitrary lattices.
Once we have shown that the steady state after the application of the completely positive map lies within the desired subspace (the ground-state space of the frustration-free Hamiltonian), the next question to be addressed is how efficient the process is. This depends on the spectral gap, δ, of the completely positive map (or, equivalently, of the corresponding Liouvillian), as the time to reach the steady state,  . Thus, the above procedure will be efficient as long as the gap vanishes only polynomially with the number of systems, N. Similarly to what occurs with many-body Hamiltonians, the determination of such a gap is, in general, very complicated. For a wide range of interesting models, however, it can be proved that this gap scales favourably. This is the case for all MPS as well as for a rich subfamily of PEPS that includes all stabilizer states (such as Kitaev’s toric code11 and the Levin–Wen states12). In the Methods section, we characterize such a subfamily of states, and in Supplementary Information we give the technical proofs of our statements. Here, we will qualitatively explain how our method works efficiently for some families of states. For that we note that the action of the completely positive map (2) can be interpreted as randomly choosing a region λ (according to pλ, which we may set equal to 1/N), then measuring Pλ and applying a correction according to the unitaries if the outcome was negative. We denote by Rn the set of regions λ where ϕ satisfies the condition Hλ|ϕ〉=0. If we measure now in one of those regions, we will obviously obtain a positive result, and thus Rn will remain the same. If we measure in another region, we may have a positive or negative result, something that may change the set Rn. By imposing certain conditions on the operators Hλ and Uλ,i, we can make sure that in each step Rn cannot be reduced and that the probability of being enlarged is non-vanishing. This automatically ensures that the τ scales only polynomially with the number of systems. In one dimension, however, one can get rid of all those restrictions and show that any MPS can be prepared in a time that also scales favourably with N. The fact that all MPS states can be prepared with our method, together with the results reported in refs 23, 24, automatically implies the existence of phase transitions driven by dissipation in the following sense. By changing the parameters of the operators Hλ appearing in the completely positive map (2), we change the steady state of that map. It is possible to choose models for which that state changes abruptly at some particular value of that parameter in such a way that the correlation length diverges and an order parameter appears (an example can be found in the Supplementary Information).
. Thus, the above procedure will be efficient as long as the gap vanishes only polynomially with the number of systems, N. Similarly to what occurs with many-body Hamiltonians, the determination of such a gap is, in general, very complicated. For a wide range of interesting models, however, it can be proved that this gap scales favourably. This is the case for all MPS as well as for a rich subfamily of PEPS that includes all stabilizer states (such as Kitaev’s toric code11 and the Levin–Wen states12). In the Methods section, we characterize such a subfamily of states, and in Supplementary Information we give the technical proofs of our statements. Here, we will qualitatively explain how our method works efficiently for some families of states. For that we note that the action of the completely positive map (2) can be interpreted as randomly choosing a region λ (according to pλ, which we may set equal to 1/N), then measuring Pλ and applying a correction according to the unitaries if the outcome was negative. We denote by Rn the set of regions λ where ϕ satisfies the condition Hλ|ϕ〉=0. If we measure now in one of those regions, we will obviously obtain a positive result, and thus Rn will remain the same. If we measure in another region, we may have a positive or negative result, something that may change the set Rn. By imposing certain conditions on the operators Hλ and Uλ,i, we can make sure that in each step Rn cannot be reduced and that the probability of being enlarged is non-vanishing. This automatically ensures that the τ scales only polynomially with the number of systems. In one dimension, however, one can get rid of all those restrictions and show that any MPS can be prepared in a time that also scales favourably with N. The fact that all MPS states can be prepared with our method, together with the results reported in refs 23, 24, automatically implies the existence of phase transitions driven by dissipation in the following sense. By changing the parameters of the operators Hλ appearing in the completely positive map (2), we change the steady state of that map. It is possible to choose models for which that state changes abruptly at some particular value of that parameter in such a way that the correlation length diverges and an order parameter appears (an example can be found in the Supplementary Information).
We have investigated the computational power of purely dissipative processes, and proved that it is equivalent to that of the quantum circuit model of quantum computation. We have also shown that dissipative dynamics can be used to create ground states (such as MPS or PEPS) of frustration-free Hamiltonians of strongly correlated quantum spin systems. We believe that these new methods can be experimentally tested using atoms or ions with current set-ups (see the Methods section).
Let us stress that we have been concerned here with a proof-of-principle demonstration that dissipation provides us with an alternative way of carrying out quantum computations or state engineering. We believe, however, that much more efficient and practical schemes can be developed and adapted to specific implementations. We also think that these results open up some interesting questions that deserve further investigation: for example, how the use of fault-tolerant computations can make our scheme more robust, or how one can design translationally invariant completely positive maps that prepare MPS more efficiently, or the importance and generality of the set of commuting Hamiltonians (see the Methods section), which is intimately connected to the fixed points of the renormalization group transformations on PEPS (as it happens with MPS; ref. 25). Furthermore, the model of DQC might well lead to the construction of new quantum algorithms, as, for example, quantum random walks can more easily be formulated within this context. Finally, other ideas related to this work can be easily addressed using the methods introduced; for example, thermal states of commuting Hamiltonians can be engineered using DSE because the Metropolis way of sampling over classical spin configurations can be adopted to the case of commuting operators. Similar techniques could be applied to free fermionic and bosonic systems, and, more generally, it should be possible to devise DSE schemes converging to the ground or thermal states of frustrated Hamiltonians by combining unitary and dissipative dynamics.
Note added. Concurrently with the submission of this paper, refs 26 and 27 appeared in which a similar quantum-reservoir engineering was used to prepare many-body states and non-equilibrium quantum phases.
Methods
Engineering dissipation.
Here we show how to engineer the local dissipation that gives rise to the master equations (1) and completely positive maps (2). They are composed of local terms, involving few particles (typically two), so that we just have to show how to implement those. To simplify the exposition, we will treat those particles as a single one and assume that one has full control over its dynamics (for example, one can apply arbitrary gates).
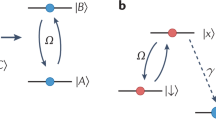
Let us start with the completely positive maps. It is clear that by applying a quantum gate to the particle and a ‘fresh’ ancilla and then tracing the ancilla one can generate any physical action (that is, completely positive map) on the system. Furthermore, by repeating the same process with short time intervals one can subject the system to an arbitrary time-independent master equation. This last process may not be efficient. An alternative way works as follows. Let us assume that the ancilla is a qubit interacting with a reservoir such that it fulfils a master equation with Liouville operator  , where σ−=|0〉〈1|. Now, we couple the ancilla to the system with a Hamiltonian H=Ω(σ−L†+σ−†L). In the limit Γ≫Ω, one can adiabatically eliminate the level |1〉 of the ancilla28 by applying second-order perturbation theory to the Liouvillian (albeit for non-Hermitian operators). In this way we obtain an effective master equation for ρ describing the system alone, with Liouville operator
, where σ−=|0〉〈1|. Now, we couple the ancilla to the system with a Hamiltonian H=Ω(σ−L†+σ−†L). In the limit Γ≫Ω, one can adiabatically eliminate the level |1〉 of the ancilla28 by applying second-order perturbation theory to the Liouvillian (albeit for non-Hermitian operators). In this way we obtain an effective master equation for ρ describing the system alone, with Liouville operator  . By using several ancillas with Hamiltonians H=Ω(σ−Li+σ−†Li†) and following the same procedure we obtain the desired master equation. Although we have not specified here a physical system, one could use atoms. In that case, the ancilla could be an atom itself with |0〉 and |1〉 an electronic ground and excited level, respectively, so that spontaneous emission gives rise to the dissipation. The coupling to the system (other atoms) could be achieved using standard ideas used in the implementation of quantum computation using those systems13.
. By using several ancillas with Hamiltonians H=Ω(σ−Li+σ−†Li†) and following the same procedure we obtain the desired master equation. Although we have not specified here a physical system, one could use atoms. In that case, the ancilla could be an atom itself with |0〉 and |1〉 an electronic ground and excited level, respectively, so that spontaneous emission gives rise to the dissipation. The coupling to the system (other atoms) could be achieved using standard ideas used in the implementation of quantum computation using those systems13.
Efficient state preparation.
We have shown that it is possible to engineer dissipative processes that prepare ground states of frustration-free Hamiltonians in steady state. In the proof, the time for this preparation scales as NN, which may be an issue for experiments with large number of particles. Here we give much more efficient methods for certain classes of frustration-free Hamiltonians.
We consider first frustration-free Hamiltonians for which [Hλ,Hμ]=0 and show that, under certain conditions, the corresponding ground states can be prepared in a time that scales only polynomially with the number of particles. The corresponding set of ground states contains important families, such as stabilizer states (for example, cluster states and topological codes), or certain kinds of PEPS, namely, those that have (commuting) parent Hamiltonians with the injectivity condition (as defined in refs 8, 29). Note that there was no known way of efficient preparation for the latter.
Loosely speaking, we will consider two classes of Hamiltonians. (1) Hamiltonians for which all excitations can be locally annihilated. In this case the time of convergence scales as  . (2) Interactions where excitations have to be moved along the lattice before they can annihilate and
. (2) Interactions where excitations have to be moved along the lattice before they can annihilate and  .
.
To see how the first case can occur notice that, when iterating  , the correction on λ does not change the outcome of previous measurements on neighbouring regions because
, the correction on λ does not change the outcome of previous measurements on neighbouring regions because

In fact, this can always be achieved by regrouping the regions into larger ones having an interior  on which only Hλacts non-trivially and letting the Uλ,i solely act on I(λ). Denote by q the largest probability for obtaining twice a negative measurement outcome on the same region λ. The energy
on which only Hλacts non-trivially and letting the Uλ,i solely act on I(λ). Denote by q the largest probability for obtaining twice a negative measurement outcome on the same region λ. The energy  after M applications of
after M applications of  decreases then as N(1−(1−q)/N)M such that it takes
decreases then as N(1−(1−q)/N)M such that it takes  steps to converge to a ground state. The relaxation time of the corresponding Liouvillian is thus
steps to converge to a ground state. The relaxation time of the corresponding Liouvillian is thus  . Clearly, this is a reasonable bound only if q<1, a condition possibly incompatible with equation (3).
. Clearly, this is a reasonable bound only if q<1, a condition possibly incompatible with equation (3).
Note that for all stabilizer states we can achieve q=0, because there exists always a local unitary (acting on a single qubit) so that HλUλHλ=0. A class of stabilizer states where this is compatible with equation (3) are the so-called graph states10. In this case, λ labels (with some abuse of notation) a vertex of a graph and  , where σ(λ)is a Pauli operator acting on site λ and
, where σ(λ)is a Pauli operator acting on site λ and  is the set of edges of the graph. Obviously, Uλ=σz(λ) does the job. In this special case, we can get even faster convergence when using the Liouvillian
is the set of edges of the graph. Obviously, Uλ=σz(λ) does the job. In this special case, we can get even faster convergence when using the Liouvillian

The corresponding relaxation time can be determined exactly by realizing that the spectrum of  equals that of
equals that of  so that τ=1 (see Supplementary Information).
so that τ=1 (see Supplementary Information).
For the second type of commuting Hamiltonians, equation (3) and q<1 are incompatible. However, we can still prove fast convergence by relaxing equation (3) such that within each region λ the Uλ acts on a site closest to a predetermined site (say the origin) on the lattice and thus commutes with all terms Hλ that are further away (see Supplementary Information for details). In this way excitations are moved over the lattice before they can annihilate. As this requires extra time proportional to the system’s size, we get  .
.
We turn now to another family of ground states of frustration-free Hamiltonians, namely MPS (ref. 9). For the sake of clearness, we will consider here translationally invariant Hamiltonians, although the analysis can be straightforwardly extended to systems without that symmetry. We will specify a completely positive map to prepare states of the form

where the A terms are D×D matrices. We assume the injectivity property29, which implies that Ψ is the unique ground state of a nearest-neighbour frustration-free ‘parent’ Hamiltonian that has a gap. Denoting by ρ the reduced density operator corresponding to particles k and k+1, Hk and Pk=1−Hk will denote the projectors onto its kernel and range, respectively. Note that tr(Pk)=D2. We take N=2n for simplicity, but this is clearly not necessary. We construct the channel  in several steps. We first define a channel acting on two neighbouring particles k,k+1, as follows
in several steps. We first define a channel acting on two neighbouring particles k,k+1, as follows

Here, k=2r−1(2c−1), where r=1,…,n and c=1,…,2n−r. The action of these maps has a tree structure, where the index rindicates the row in the tree, whereas c does it for the column. Now we define recursively,

Here, r=2,…,n, c=1,…,2n−r,  and εr+1=1/Mr, where M=C N2 and C≫1 (see Supplementary Information). Note that
and εr+1=1/Mr, where M=C N2 and C≫1 (see Supplementary Information). Note that  acts on the first 2r particles,
acts on the first 2r particles,  on the next 2r and so on. We finally define
on the next 2r and so on. We finally define

In the Supplementary Information, we show that this map achieves the fixed point (up to an exponentially small error in C) in a time  . The intuition behind the completely positive map (4) is that the channels
. The intuition behind the completely positive map (4) is that the channels  , which are the ones that most often applied, project the state of every second nearest neighbour onto the right subspace. Then
, which are the ones that most often applied, project the state of every second nearest neighbour onto the right subspace. Then  do the same with half of the pairs that have not been projected. Then
do the same with half of the pairs that have not been projected. Then  does the same on half of the rest, and so on.
does the same on half of the rest, and so on.
References
Aliferis, P., Gottesman, D. & Preskill, J. Quantum accuracy threshold for concatenated distance-3 codes. Quant. Inf. Comput. 6, 97–165 (2006).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).
Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488 (1982).
Fannes, M., Nachtergaele, B. & Werner, R. F. Finitely correlated states on quantum spin chains. Commun. Math. Phys. 144, 443–490 (1992).
Verstraete, F. & Cirac, J. I. Renormalization algorithms for quantum-many body systems in two and higher dimensions. Preprint at <http://arxiv.org/abs/cond-mat/0407066> (2004).
DiVincenzo, D. P. The physical implementation of quantum computation. Fortschr. Phys. 48, 771–783 (2000).
Poyatos, J. F., Cirac, J. I. & Zoller, P. Quantum Reservoir Engineering with laser cooled trapped ions. Phys. Rev. Lett. 77, 4728–4731 (1996).
Perez-Garcia, D., Verstraete, F., Wolf, M. M. & Cirac, J. I. Matrix product state representations. Quant. Inf. Comput. 7, 401–430 (2007).
Verstraete, F., Murg, V. & Cirac, J. I. Matrix product states, projected entangled pair states, and variational renormalization group methods for quantum spin systems. Adv. Phys. 57, 143–224 (2008).
Briegel, H. J. & Raussendorf, R. Persistent entanglement in arrays of interacting qubits. Phys. Rev. Lett. 86, 910–913 (2001).
Kitaev, A. Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2–30 (2003).
Levin, M. A. & Wen, X. G. String-net condensation: A physical mechanism for topological phases. Phys. Rev. B 71, 045110 (2005).
Cirac, J. I. & Zoller, P. New frontiers in quantum information with atoms and ions. Phys. Today 57, 38–44 (2004).
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008).
Leibfried, D., Blatt, R., Monroe, C. & Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 75, 281–324 (2003).
Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 48, 119–130 (1976).
Kempe, J., Kitaev, A. Y. & Regev, O. The complexity of the local Hamiltonian problem. SIAM J. Comput. 35, 1070–1097 (2004).
Aharonov, D. et al. Adiabatic quantum computation is equivalent to standard quantum computation. SIAM J. Comput. 37, 166–194 (2007).
Kempe, J. Quantum random walks—an introductory overview. Contemp. Phys. 44, 307–327 (2003).
Arora, S. & Safra, S. Probabilistic checking of proofs: A new characterization of NP. J. ACM 45, 70–122 (1998).
Gottesman, D. A theory of fault-tolerant quantum computation. Phys. Rev. A 57, 127–137 (1998).
Wolf, M. M. & Cirac, J. I. Dividing quantum channels. Commun. Math. Phys. 279, 147–168 (2008).
Wolf, M. M., Ortiz, G., Verstraete, F. & Cirac, J. I. Quantum phase transitions in matrix product systems. Phys. Rev. Lett. 97, 110403 (2006).
Verstraete, F., Wolf, M. M., Perez-Garcia, D. & Cirac, J. I. Criticality, the area law, and the computational power of PEPS. Phys. Rev. Lett. 96, 220601 (2006).
Verstraete, F., Cirac, J. I., Latorre, J. I., Rico, E. & Wolf, M. M. Renormalization-group transformations on quantum states. Phys. Rev. Lett. 94, 140601 (2005).
Diehl, S. et al. Quantum states and phases in driven open quantum systems with cold atoms. Nature Phys. 4, 878–883 (2008).
Kraus, B. et al. Preparation of entangled states by quantum Markov processes. Phys. Rev. A 78, 042307 (2008).
Cohen-Tannoudji, C., Dupont-Roc, J. & Grynberg, G. Atom-Photon Interactions (Wiley, 1992).
Perez-Garcia, D., Verstraete, F., Cirac, J. I. & Wolf, M. M. PEPS as unique ground states of local Hamiltonians. Quant. Inf. Comput. 8, 0650–0663 (2008).
Acknowledgements
We thank D. Perez-Garcia for discussions and acknowledge financial support by the EU projects QUEVADIS, SCALA, the FWF, QUANTOP, FNU, SFB FoQuS, the DFG, Forschungsgruppe 635, the Munich Center for Advanced Photonics (MAP) and Caixa Manresa.
Author information
Authors and Affiliations
Contributions
All authors have contributed equally to this paper.
Corresponding authors
Supplementary information
Supplementary Information
Supplementary Information (PDF 173 kb)
Rights and permissions
About this article
Cite this article
Verstraete, F., Wolf, M. & Ignacio Cirac, J. Quantum computation and quantum-state engineering driven by dissipation. Nature Phys 5, 633–636 (2009). https://doi.org/10.1038/nphys1342
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1342
This article is cited by
-
Autonomous error correction of a single logical qubit using two transmons
Nature Communications (2024)
-
Generating quantum channels from functions on discrete sets
Quantum Information Processing (2024)
-
Characterizing a non-equilibrium phase transition on a quantum computer
Nature Physics (2023)
-
Many-body cavity quantum electrodynamics with driven inhomogeneous emitters
Nature (2023)
-
Non-Abelian effects in dissipative photonic topological lattices
Nature Communications (2023)