Abstract
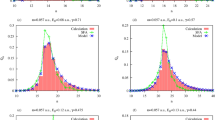
The properties of random and fluctuating systems are often studied through the use of Gaussian distributions. However, in a number of situations, rare events have drastic consequences, which cannot be explained by Gaussian statistics. Considerable efforts have thus been devoted to the study of non-Gaussian fluctuations such as Lévy statistics, generalizing the standard description of random walks. Unfortunately, only macroscopic signatures, obtained by averaging over many random steps, are usually observed in physical systems. We present experimental results investigating the elementary process of anomalous diffusion of photons in hot atomic vapours. We measure the step-size distribution of the random walk and show that it follows a power-law characteristic of Lévy flights.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Lévy, P. Theorie de l’Addition des Variables Aleatoires (Gauthier-Villiers, 1937).
Bouchaud, J.-P. & Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 195, 127–293 (1990).
Shlesinger, M., Zaslavsky, G. & Frisch, U. Lévy Flights and Related Topics in Physics (Springer, 1995).
Metzler, R. & Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 339, 1–77 (2000).
Bouchaud, J.-P. & Potters, M. Theory of Financial Risk and Derivative Pricing (Cambridge Univ. Press, 2003).
Botet, R. & Ploszajczak, M. Universal Fluctuations (World Scientific, 2002).
Goldenfeld, N. D. Lectures on Phase Transitions and the Renormalisation Group (Addison, 1992).
Barthelemy, P., Bertolotti, J. & Wiersma, D. S. A Lévy flight for light. Nature 453, 495–498 (2008).
Springmann, U. Multiple resonance line scattering and the momentum problem in Wolf-Rayet star winds. Astron. Astrophys. 289, 505–523 (1994).
Molisch, A. F. & Oehry, B. P. Radiation Trapping in Atomic Vapours (Oxford Univ., 1998).
Holstein, T. Imprisonment of resonance radiation in gases. Phys. Rev. 72, 1212–1233 (1947).
Kenty, C. On radiation diffusion and the rapidity of escape of resonance radiation from a gas. Phys. Rev. 42, 823–842 (1932).
Fioretti, A., Molisch, A. F., Mutter, J. H., Verkerk, P. & Allegrini, M. Observation of radiation trapping in a dense Cs magneto-optical trap. Opt. Commun. 149, 415–422 (1998).
Labeyrie, G. et al. Slow diffusion of light in a cold atomic cloud. Phys. Rev. Lett. 91, 223904 (2003).
Labeyrie, G., Kaiser, R. & Delande, D. Radiation trapping in a cold atomic gas. Appl. Phys. B 81, 1001–1008 (2005).
Pereira, E., Martinho, J. M. G. & Berberan-Santos, M. N. Photon trajectories in incoherent atomic radiation trapping as Lévy flights. Phys. Rev. Lett. 93, 120201 (2004).
Alves-Pereira, A. R., Nunes-Pereira, E. J., Martinho, J. M. G. & Berberan-Santos, M. N. Photonic superdiffusive motion in resonance line radiation trapping partial frequency redistribution effects. J. Chem. Phys. 126, 154505 (2007).
Mantegna, R. N. & Stanley, H. E. Stochastic process with ultraslow convergence to a Gaussian: The truncated Lévy flight. Phys. Rev. Lett. 73, 2946–2949 (1994).
Acknowledgements
We acknowledge financial support from the program ANR-06-BLAN-0096 and financial support for N.M. by DGA.
Author information
Authors and Affiliations
Contributions
N.M. contributed to planning of the project, laboratory measurements, data analysis and analytical calculations. W.G. contributed to planning of the project and data interpretation. M.C. contributed to numerical simulations. R.K. contributed to the conception and coordination of the project and to interpretation of results.
Corresponding author
Rights and permissions
About this article
Cite this article
Mercadier, N., Guerin, W., Chevrollier, M. et al. Lévy flights of photons in hot atomic vapours. Nature Phys 5, 602–605 (2009). https://doi.org/10.1038/nphys1286
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1286
This article is cited by
-
Quantitative analysis of the intensity distribution of optical rogue waves
Communications Physics (2024)
-
Delay time of waves performing Lévy walks in 1D random media
Scientific Reports (2020)
-
Disordered photonics
Nature Photonics (2013)