Abstract
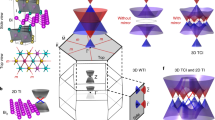
Topological insulators are new states of quantum matter in which surface states residing in the bulk insulating gap of such systems are protected by time-reversal symmetry. The study of such states was originally inspired by the robustness to scattering of conducting edge states in quantum Hall systems. Recently, such analogies have resulted in the discovery of topologically protected states in two-dimensional and three-dimensional band insulators with large spin–orbit coupling. So far, the only known three-dimensional topological insulator is BixSb1−x, which is an alloy with complex surface states. Here, we present the results of first-principles electronic structure calculations of the layered, stoichiometric crystals Sb2Te3, Sb2Se3, Bi2Te3 and Bi2Se3. Our calculations predict that Sb2Te3, Bi2Te3 and Bi2Se3 are topological insulators, whereas Sb2Se3 is not. These topological insulators have robust and simple surface states consisting of a single Dirac cone at the Γ point. In addition, we predict that Bi2Se3 has a topologically non-trivial energy gap of 0.3 eV, which is larger than the energy scale of room temperature. We further present a simple and unified continuum model that captures the salient topological features of this class of materials.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Kane, C. L. & Mele, E. J. Quantum spin hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Bernevig, B. A. & Zhang, S. C. Quantum spin hall effect. Phys. Rev. Lett. 96, 106802 (2006).
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Murakami, S. Quantum spin hall effect and enhanced magnetic response by spin–orbit coupling. Phys. Rev. Lett. 97, 236805 (2006).
Bernevig, B. A., Hughes, T. L. & Zhang, S. C. Quantum spin hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).
König, M. et al. Quantum spin hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).
Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Moore, J. E. & Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306 (2007).
Roy, R. On the Z2 classification of quantum spin hall models. Preprint at <http://arxiv.org/abs/cond-mat/0604211> (2006).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Dai, X., Hughes, T. L., Qi, X.-L., Fang, Z. & Zhang, S.-C. Helical edge and surface states in HgTe quantum wells and bulk insulators. Phys. Rev. B 77, 125319 (2008).
Hsieh, D. et al. A topological dirac insulator in a quantum spin hall phase. Nature 452, 970–974 (2008).
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Fang, Z. & Terakura, K. Structural distortion and magnetism in transition metal oxides: Crucial roles of orbital degrees of freedom. J. Phys. Condens. Matter 14, 3001–3014 (2002).
Mishra, S. K., Satpathy, S. & Jepsen, O. Electronic structure and thermoelectric properties of bismuth telluride and bismuth selenide. J. Phys. Condens. Matter 9, 461–470 (1997).
Larson, P. Effects of uniaxial and hydrostatic pressure on the valence band maximum in Sb2Te3: An electronic structure study. Phys. Rev. B 74, 205113 (2006).
Black, J., Conwell, E. M., Seigle, L. & Spencer, C. W. Electrical and optical properties of some M2-N3-semiconductors. J. Phys. Chem. Solids 2, 240–251 (1957).
Mooser, E. & Pearson, W. B. New semiconducting compounds. Phys. Rev. 101, 492–493 (1956).
Wittel, K. & Manne, R. Atomic spin–orbit interaction parameters from spectral data for 19 elements. Theor. Chim. Acta 33, 347–349 (1974).
Marzari, N. & Vanderbilt, D. Maximally localized generalized wannier functions for composite energy bands. Phys. Rev. B 56, 12847–12865 (1997).
Souza, I., Marzari, N. & Vanderbilt, D. Maximally localized wannier functions for entangled energy bands. Phys. Rev. B 65, 035109 (2001).
Sancho, M. P. L., Sancho, J. M. L. & Rubio, J. Quick iterative scheme for the calculation of transfer matrices: Application to Mo (100). J. Phys. F 14, 1205–1215 (1984).
Sancho, M. P. L., Sancho, J. M. L., Sancho, J. M. L. & Rubio, J. Highly convergent schemes for the calculation of bulk and surface green functions. J. Phys. F 15, 851–858 (1985).
Winkler, R. Spin–Orbit Coupling Effects in Two-Dimensional Electron and Hole Systems (Springer Tracts in Modern Physics, Vol. 191, Springer, 2003).
Koenig, M. et al. The quantum spin hall effect: Theory and experiment. J. Phys. Soc. Japan 77, 031007 (2008).
Noh, H.-J. et al. Spin–orbit interaction effect in the electronic structure of Bi2Te3 observed by angle-resolved photoemission spectroscopy. Europhys. Lett. 81, 57006 (2008).
Urazhdin, S. et al. Surface effects in layered semiconductors Bi2Se3 and Bi2Te3 . Phys. Rev. B 69, 085313 (2004).
Xia, Y. et al. Electrons on the surface of Bi2Se3 form a topologically-ordered two dimensional gas with a non-trivial berry’s phase. Preprint at <http://arxiv.org/abs/0812.2078> (2008).
Qi, X.-L., Li, R.-D., Zang, J. & Zhang, S.-C. Inducing a magnetic monopole with topological surface states. Science 323, 1184–1187 (2009).
Acknowledgements
We would like to thank B. F. Zhu for the helpful discussion. This work is supported by the NSF of China, the National Basic Research Program of China (No. 2007CB925000), the International Science and Technology Cooperation Program of China (No. 2008DFB00170) and by the US Department of Energy, Office of Basic Energy Sciences under contract DE-AC02-76SF00515.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhang, H., Liu, CX., Qi, XL. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nature Phys 5, 438–442 (2009). https://doi.org/10.1038/nphys1270
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1270
This article is cited by
-
Topological minibands and interaction driven quantum anomalous Hall state in topological insulator based moiré heterostructures
Nature Communications (2024)
-
Enhanced electrical properties of amorphous In-Sn-Zn oxides through heterostructuring with Bi2Se3 topological insulators
Scientific Reports (2024)
-
Superconductivity in unconventional metals
npj Computational Materials (2024)
-
Review of 2D Bi2X3 (X = S, Se, Te): from preparation to photodetector
Rare Metals (2024)
-
Topological Insulator TlBiSe2/GaN Vertical Heterojunction Diode for High Responsive Broadband UV to Near-Infrared Photodetector
Journal of Electronic Materials (2024)