One-dimensional topologically protected modes in topological insulators with lattice dislocations

Abstract

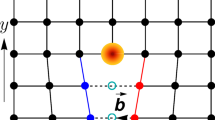
Topological defects, such as domain walls and vortices, have long fascinated physicists. A novel twist is added in quantum systems such as the B-phase of superfluid helium He₃, where vortices are associated with low-energy excitations in the cores. Similarly, cosmic strings may be tied to propagating fermion modes. Can analogous phenomena occur in crystalline solids that host a plethora of topological defects? Here, we show that indeed dislocation lines are associated with one-dimensional fermionic excitations in a ‘topological insulator’, a novel phase of matter believed to be realized in the material Bi_0.9Sb_0.1. In contrast to fermionic excitations in a regular quantum wire, these modes are topologically protected and not scattered by disorder. As dislocations are ubiquitous in real materials, these excitations could dominate spin and charge transport in topological insulators. Our results provide a novel route to creating a potentially ideal quantum wire in a bulk solid.