Abstract
A fundamental challenge in the design of microfluidic devices lies in the need to control the transport of fluid according to complex patterns in space and time, and with sufficient accuracy. Although strategies based on externally actuated valves have enabled marked breakthroughs in chip-based analysis1,2,3,4,5, this requires significant off-chip hardware, such as vacuum pumps and switching solenoids, which strongly tethers such devices to laboratory environments6,7,8,9,10. Severing the microfluidic chip from this off-chip hardware would enable a new generation of devices that place the power of microfluidics in a broader range of disciplines. For example, complete on-chip flow control would empower highly portable microfluidic tools for diagnostics, forensics, environmental analysis and food safety, and be particularly useful in field settings where infrastructure is limited. Here, we demonstrate an elegantly simple strategy for flow control: fluidic networks with embedded deformable features are shown to transport fluid selectively in response to the frequency of a time-modulated pressure source. Distinct fluidic flow patterns are activated through the dynamic control of a single pressure input, akin to the analog responses of passive electrical circuits composed of resistors, capacitors and diodes.
Similar content being viewed by others
Main
Although the concept of fluidic diodes (check valves) is not new11,12, the combinatorial effect provided by discrete, deformable elastomer features that function as fluidic analogues to electronic capacitors and diodes should introduce powerful dynamic characteristics into a fluidic network. It is shown here that the dynamic responses of fluidic circuits can be programmed a priori by combining these types of feature as suggested by conventional circuit analysis.
The dynamics of laminar incompressible flow inside a channel are described approximately by:  , where Δp is the pressure change from one end of the channel to the other and q is the volumetric flow rate. (Dots denote time derivatives.) For example, the fluidic resistance of a rectangular channel that is much wider than its depth is given by R=[12μ LRf(d/w)]/d3w (ref. 13) (see Supplementary Information, equation S1), where μ is the fluid viscosity and LR, w and d are the channel length, width and depth, respectively. f(d/w) is a dimensionless function that approaches unity in the limit that d≪w. The inertia associated with accelerating flows introduces fluidic inductance, L. For a rectangular channel, L=ρ LR/A, where ρ is the density of the fluid and A is the cross-sectional area of the channel. Similar results have been derived and experimentally validated for channels with different geometries14. For water in submillimetre channels, the characteristic timescale τ1=L/R is of the order of milliseconds; this implies inductance can be neglected for driving frequencies less than 30 Hz (ref. 15).
, where Δp is the pressure change from one end of the channel to the other and q is the volumetric flow rate. (Dots denote time derivatives.) For example, the fluidic resistance of a rectangular channel that is much wider than its depth is given by R=[12μ LRf(d/w)]/d3w (ref. 13) (see Supplementary Information, equation S1), where μ is the fluid viscosity and LR, w and d are the channel length, width and depth, respectively. f(d/w) is a dimensionless function that approaches unity in the limit that d≪w. The inertia associated with accelerating flows introduces fluidic inductance, L. For a rectangular channel, L=ρ LR/A, where ρ is the density of the fluid and A is the cross-sectional area of the channel. Similar results have been derived and experimentally validated for channels with different geometries14. For water in submillimetre channels, the characteristic timescale τ1=L/R is of the order of milliseconds; this implies inductance can be neglected for driving frequencies less than 30 Hz (ref. 15).
The fluidic capacitors are deformable elastomer films that are bonded over a widened portion of a microchannel that is part of the fluidic network, as shown in Fig. 1a. As the pressure increases inside the network (relative to the outside pressure), fluid is stored in the deformed bulge, much like an electrical capacitor stores charge. The dynamic characteristic of the capacitor is described by  , where q is the volumetric flow rate and
, where q is the volumetric flow rate and  is the time derivative of the pressure difference between opposing sides of the film. The pre-factor, C, is the fluidic capacitance, which represents the volume stored under the deformed film per unit pressure. It can be determined from elementary solid mechanics solutions, as described in ref. 16. A simple case is a circular capacitor that exhibits small motion relative to the film thickness; the capacitance is described by C=16 r6/3E h3, where r is the planar radius of the capacitor and E and h are the elastic modulus and thickness of the film, respectively. The treatment of an elliptical capacitor (plate), as used in the current work, is given in Supplementary Information, equations S2–S4. As shown in the results to follow, just as in their electronic counterparts, fluidic networks containing a capacitor (a deformable film) and a resistor (conventional microchannel) are linear circuits with a characteristic time constant τ2=R C. In the same way, this fluidic time constant—and as such the frequency response of a fluidic R C branch—can be programmed over a broad range by modulating the dimensions of the channels and capacitor film.
is the time derivative of the pressure difference between opposing sides of the film. The pre-factor, C, is the fluidic capacitance, which represents the volume stored under the deformed film per unit pressure. It can be determined from elementary solid mechanics solutions, as described in ref. 16. A simple case is a circular capacitor that exhibits small motion relative to the film thickness; the capacitance is described by C=16 r6/3E h3, where r is the planar radius of the capacitor and E and h are the elastic modulus and thickness of the film, respectively. The treatment of an elliptical capacitor (plate), as used in the current work, is given in Supplementary Information, equations S2–S4. As shown in the results to follow, just as in their electronic counterparts, fluidic networks containing a capacitor (a deformable film) and a resistor (conventional microchannel) are linear circuits with a characteristic time constant τ2=R C. In the same way, this fluidic time constant—and as such the frequency response of a fluidic R C branch—can be programmed over a broad range by modulating the dimensions of the channels and capacitor film.
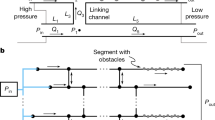
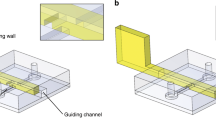
a, Discrete fluidic capacitors are created by bonding deformable films (in this case, PDMS) over reservoirs placed in the network between fluidic channels (resistors) fabricated in glass. These features store and release fluid (volumetric flow rate, qC) in proportion to the time rate of change in pressure inside the network; the proportionality constant (capacitance, C) depends on film thickness (h), span (a, b) and elastic modulus (E), and can be predicted using classical mechanics solutions (see governing equations in Supplementary Information). b, Discrete fluidic diodes are created by bonding deformable films around weirs that separate two channels in the network. When the internal pressure is larger than the external pressure, the diode opens and exhibits nonlinear pressure–flow relationships (volumetric flow rate, qD) dictated by solid–fluid coupling. When the internal pressure is less than the external pressure, the diode pulls shut and prevents flow.
The elementary function of the diodes (Fig. 1b) is to permit flow in the forward direction for internal network pressures above ambient pressure (that acting on the top of the diode), and obstruct flow in the reverse direction for internal network pressures below ambient pressure. On top of this inherent asymmetry, this fluidic diode implementation introduces an extra nonlinearity, in that the flow rate for an open diode is a nonlinear function of pressure. This can be understood by considering the open diode as a resistive channel in which the depth (and, hence, resistance) is governed by the pressure pushing the diode film upwards. If the pressure downstream is negligible compared with that driving flow, the pressure–flow relationship of the diode is given by: q=D p4 for p>patm, where D∝LD11w/(μ E3h9) and LD is the characteristic length of the open diode14. For network pressures less than the external pressure on top of the film, the diode pulls shut and does not allow flow. The very strong power-law dependence on film properties and pressure arises from the fact that the resistance of the open diode depends strongly on the resulting gap size.
The validity of the fluidic capacitance framework is illustrated in Fig. 2. Flow inside the channel is initiated by applying a periodic pressure pulse to the top of the input capacitor, Cin. A square-wave pressure signal, P(ω t) (oscillating between near-vacuum and atmospheric pressure, Fig. 2a), was generated using a conventional vacuum source and an electromagnetic switching solenoid. The dynamic response of the circuit was characterized across a broad range of excitation frequencies, by measuring the deflection of the input and output capacitors using extrinsic Fabry–Perot interferometry17 (EFPI; Fig. 2a–c). Fluidic resistances and capacitances, as well as capacitor stiffness values, were related to these deflection measurements in Supplementary Information, equations S5,S6. To corroborate the linear circuit behaviour, three chips with different combinations of capacitors and resistors were used. Two chips had identical channels (resistors) (Chips 1a and 1b), with the only difference being the thickness of the output capacitor film. The third chip (Chip 2) had identical capacitors to Chip 1a, with different channel dimensions (that is, different resistances from Chips 1a or 1b). Thus, the time constants of the three networks (τ2=R C) were programmed to be distinct by independently varying both the fluidic resistances and capacitances. A complete list of dimensions and associated fluidic properties of the features are given in Supplementary Information, Tables S1,S2.
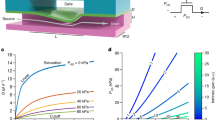
a, Chip architecture showing locations where capacitor deflections (δ) were measured with EFPI. Fluidic resistors (R1−R3), the actuated input (Cin) and passive output (Cout) capacitors are labelled, along with the periodic pressure pulse input (P(ω t)). Deflection versus driving frequency data are shown for Chip 1a. As predicted, the Cin deflection (black data points) showed low-pass behaviour, and the Cout deflection (red data points) exhibited a band-pass response from these reference points. b, Examples of temporal responses of the same network (Chip 1a) illustrated by the deflection of the actuated capacitor, Cin (black trace, top), and passive capacitor, Cout (red trace, bottom), at an input of 3 Hz. c, Measurements (data points) and predictions (solid lines) of the transfer function (|δout|/|δin|) between the capacitors in the linear circuit; the predictions are based on closed-form solutions for laminar flow and plate-like deformation of the capacitors, using nominal design values (that is, there are no arbitrary fitting constants). Chips 1a (red) and 1b (blue) were designed with the same fluidic resistors in their networks, but with differing Cout thicknesses; Chip 2 (green) had different fluidic resistances. The measurements and analytical predictions were in agreement, even to the degree that the asymptotic limits at high frequency were independent of capacitor thickness (details included in Supplementary Information). Error bars represent the standard deviations from three measurements conducted at each frequency.
Figure 2c illustrates the measured ratio of the deflections of the output to input capacitor films, for three different chips. These results represent the dominant amplitude component from a Fourier transform (which, as expected, corresponds to the driving frequency). The predictions from linear circuit analysis (solid lines) are superimposed on the measurements (data points). Both the theoretical predictions and the experimental data show the behaviour typical of a first-order high-pass filter from this measurement frame of reference. The response is constant above the characteristic frequency and falls off by 10 dB per decade below it. Note also that the asymptotic limits of the frequency responses are independent of capacitor thickness, as predicted by Supplementary Information, equations S5,S6, and shown in Supplementary Information, Table S3. These analytical predictions are based entirely on component properties calculated from the nominal dimensions and properties of the channels and films without any fitting constants. Supplementary Information provides complete details of the formulae and properties used in generating these predictions. It is shown in Fig. 2c that shifting the relative stiffness of the capacitors, as well as the resistance of the channels, modulates the frequency response of the network in the exact manner predicted by linear circuit analysis. The discrepancies between the measured response and analytical predictions can be easily rationalized by noting that the resistances and capacitances are very strong functions of the dimensions, such that minor fabrication-related deviations from nominal values lead to noticeable changes in response.
By combining two branches in a fluidic network with different time constants (R C properties), one can construct circuits that respond to changes in excitation frequency with differential flow contributions from each branch. Naturally, the use of components with purely linear response implies purely oscillatory responses to periodic excitation. That is, R C circuits are capable of modulating only the a.c. component of flow. To achieve frequency-dependent net volume transfer (a non-zero d.c. component of flow), nonlinear components are required. This functionality is introduced using the fluidic diodes illustrated in Fig. 1.
The powerful opportunities created by combining these diodes with R C circuits to yield a programmed frequency response of the net flow are illustrated in Figs 3 and 4. Two network branches stemming from independent reservoirs were connected into a y-shaped outlet (Fig. 3a). A single excitation source was applied simultaneously to the top of the input capacitor films in each branch (Fig. 3b). The flow contribution from each branch of the network was characterized by absorbance measurements on the output fluid, using spectrally distinct dyes in the two input reservoirs (yellow and blue dyes used for spectral analysis). Figure 4b clearly illustrates that net flow switched from one branch to the other as the excitation frequency was varied. Guided by simple governing equations (see Supplementary Information), each branch was designed to have a different characteristic frequency, at which flow amplitudes are greatest. Diodes (Fig. 1b) were positioned upstream of the junction to convert oscillatory (a.c.) flow into steady (d.c.) flow. The results demonstrate that the fluidic circuits behaved as band-pass filters with respect to the input pressure, with maximum flow from each branch occurring at its characteristic frequency (Fig. 4b). This behaviour was a consequence of the programmed frequency characteristics of the linear circuit portion of each branch; that is, the circuit behaved essentially as the combination of two first-order band-pass filters (with respect to the output) that had distinct characteristic frequencies.
a, Image of a two-branch microfluidic circuit including fluidic resistors, capacitors and diodes used to embed a specific dynamic response into the network. The high-ω0 branch was filled with a blue dye (erioglaucine diammonium), whereas the low-ω0 branch was filled with yellow dye (tartrazine) to enable spectrally distinct optical absorbance measurements to be made on the output fluid. b, Cross-section (not to scale) of chip architecture. Through the upper pneumatic channel layer (cover layer), both branches were connected to a single oscillatory pressure source, shown as a red trace, that simultaneously drove both input capacitors at a controlled frequency using a vacuum line and a single, computer-controlled solenoid valve. Both capacitor and diode membranes are shown in their upward deflection position for clarity.
a, Layout of device from Fig. 3, where, in this case, the high- and low-ω0 branches were filled with red and blue dyes, respectively, during optical imaging. b, Band-pass characteristics of the time-averaged output contributions from each branch of the network, as quantitatively determined by optical absorbance spectroscopy (using blue and yellow dyes). c, Average optical micrographs (under different actuation frequencies) of the output flow at the y-shaped node that connects the two branches (see Supplementary Information, Video S1 for further illustration). d, Examples of the temporal history (analog flow signals) of the flow contributions from each branch of the network, as determined by digital image analysis of the integrated optical intensity of each dye. e, Schematic diagram of the microdevice from a, represented as a microfluidic reagent autotitrator with a single a.c. input and d.c. output. The ratio of the high branch composition as a function of total flow is shown on the right. The pre-programmed microdevice enabled accurate, analog control over relative flow with very little peripheral instrumentation (a single pressure input). Error bars represent the standard deviations from three measurements conducted at each frequency.
The results in Fig. 4 clearly illustrate both the potential of this approach, and its inherent challenges. The controlled metering of two sources is ubiquitous in biochemical analysis, for chip-based assay calibration, reagent mixing, chemical synthesis, chromatography and so on. The current approach provides a powerful pathway towards automated metering using passive fluidic circuits. Through careful placement of the discrete components presented here, different mixing ratios (Fig. 4c,d), flow timing and elution steps can be achieved simply by changing the excitation frequency of the source (see Supplementary Information, Video S1 for an illustrative video). Critically, off-chip hardware can be replaced with on-chip functionality; a single actuation source can be used to control multiple pathways that respond in an entirely passive manner based on the component layout. In this light, the device presented in Fig. 3a could be considered a passive microfluidic autotitrator (Fig. 4e), or alternatively as an analog signal adder, that requires only a single a.c. input to control the relative ratio of the d.c. output of two solutions. Because the approach is inherently dynamic, much smaller actuation displacements are required. One does not need to achieve the large displacements required for quasi-static on–off flow control. This creates powerful new opportunities for piezoelectric or electrostatic actuation; the relatively small displacements inherent to these approaches can be exploited through dynamic coupling with the fluidic circuit.
Naturally, the central challenge is to narrow the bandwidth of the filters relative to their characteristic frequency, such that multiple channels can be selectively activated. It is clear that the bandwidth of low-frequency circuits, such as those illustrated in Fig. 4, cannot be reduced arbitrarily, owing to the inherent physical limitations of R C circuits. However, there are numerous applications where the microfluidic architecture requires only a limited number of channel branch points4,5,18. Replacing existing pneumatic valves with frequency-specific, passive flow control would reduce the requirement for off-chip hardware, substantially facilitating deployment of the chip in forensic and other field-based applications. Frequency selectivity could be improved through optimal design of R C components, and through detailed modelling of the coupled capacitance and filtering introduced by the diodes. In fact, the very same algorithms and software tools that are used for the design of electronic circuits (for example, B2-SPICE) could be used to model fluidic circuits (for example, using parameters as shown in Supplementary Information). This will facilitate the future exploitation of transient (analog) behaviour inside fluidic networks to further shape the emerging flow patterns.
Even more promising is the exploitation of fluidic inductance (the inherent inertia involved in moving fluid in the channels) at higher frequencies19. At frequencies in the 100–1,000 Hz range, inductance has a critical role even when flow is still laminar. In principle, this allows the construction of second-order filters, governed by the third fundamental time constant,  , with much steeper transfer functions. To do so, stiffer capacitors (with smaller capacitance) and higher operating frequencies (than those shown here) must be used, such that the R C constant does not dominate. Elementary circuit models illustrate that it is possible to construct true fluidic resonators in millimetre-scale devices, which exhibit bandwidths that are much smaller than the characteristic frequency19. By operating at higher frequencies, one can achieve Q-factors greater than twenty19. Provided correspondingly stiff diodes with acceptably low resistances can be developed, this has profound implications for creating highly frequency-specific, passive multi-channel fluidic networks.
, with much steeper transfer functions. To do so, stiffer capacitors (with smaller capacitance) and higher operating frequencies (than those shown here) must be used, such that the R C constant does not dominate. Elementary circuit models illustrate that it is possible to construct true fluidic resonators in millimetre-scale devices, which exhibit bandwidths that are much smaller than the characteristic frequency19. By operating at higher frequencies, one can achieve Q-factors greater than twenty19. Provided correspondingly stiff diodes with acceptably low resistances can be developed, this has profound implications for creating highly frequency-specific, passive multi-channel fluidic networks.
Methods
Microdevice fabrication.
Microdevices were fabricated as hybrid chips, with glass fluidic and pneumatic layers sandwiching a deformable polydimethylsiloxane (PDMS) layer that defined the functionality of the fluidic capacitors and diodes (see Fig. 3). Features were patterned in Borofloat glass (Schott) using standard photolithography and wet chemical etching techniques. A protocol was developed in-house to fabricate spatially discrete components with different PDMS thicknesses, that is, different fluidic capacitances. First, AZ 4210 photoresist (Clariant) was spin-coated onto a silicon wafer and baked at 90 ∘C for 2 min to serve as a release layer for the PDMS membrane. Next, a 25 or 50 μm layer of PDMS (Sylgard 184, Dow Corning) pre-polymer mixture was spin-coated onto the wafer, then cured at 70 ∘C for 2 h. The PDMS layer was then plasma bonded to a pre-fabricated layer of 290-μm-thick PDMS (Bisco Silicones), with holes punched to align above the output capacitors. Next, the PDMS assembly was released from the AZ 4210 photoresist layer (and Si wafer) using methanol. The PDMS assembly was then aligned with the glass fluidic layer and plasma bonded. Devices with diodes were protected in the diode region using a small spot of photoresist before plasma bonding, and the spot was subsequently removed using acetone. For devices in which membrane deflections were measured with an EFPI (FiberPro 2, Luna Innovations), a 50 nm layer of gold was sputtered onto the top surface of the PDMS layer (at the capacitor), and a 10 nm layer was sputtered onto the bottom surface of the glass pneumatic layer, both to define the Fabry–Perot cavity. The glass pneumatic layer was then plasma bonded to the PDMS layer to complete the device fabrication. This method was key to the design of fluidic filters, because the thickness of the intermediate PDMS layers could be varied to change the capacitance of individual components in the microfluidic circuits.
Device operation.
An oil-less diaphragm vacuum pump/compressor (Gast Manufacturing) was used to drive the pneumatic line by application of vacuum (60 kPa) or atmospheric pressure to the input capacitors. Switching between atmospheric and vacuum pressure (as shown in Fig. 3b) was accomplished using a single 12 V solenoid valve (Parker Pneumatic). A valve controller was built in-house using a single line of a quad high-side driver as a digital relay to route the 12 V power source to the solenoid valve. The valve actuation state was controlled using an in-house-written LabVIEW application through a digital output on a low-cost USB data acquisition device (USB-6008, National Instruments). The LabVIEW application stepped through frequencies from 0.05 to 25 Hz with a square-wave potential (duty cycle of 0.5) controlling the switching of the solenoid valve. As shown in Fig. 2, deflections of capacitors in response to this pressure wave were measured using an EFPI (FiberPro 2, Luna Innovations) collecting at ∼960 Hz. The optical fibre from the interferometer was positioned (orthogonal to the device) directly over the output capacitor, or coupled to the top glass layer to maintain vacuum while measuring the input capacitor deflection. The dominant amplitudes (deflection, in micrometres) of both the input and output capacitors at each driving frequency were determined with a Fourier transform, using an in-house-written Matlab script. The transfer function (plotted in Fig. 2c) was computed as the output capacitor’s dominant amplitude over the input capacitor’s dominant amplitude. Theoretical predictions and calculation of the transfer functions are described in Supplementary Information.
Flow measurements.
The microdevice was filled with different dye solutions (Sigma), tartrazine (Acid Yellow 23) and erioglaucine diammonium (Acid Blue 9), in each input channel as shown in Fig. 3. The LabVIEW application stepped through frequencies from 0.02 to 7.00 Hz with a square-wave potential on a duty cycle of 0.5. Output solution was collected over a measured period and then diluted to a known volume. The concentration of each component in the output solution was quantified using an ultraviolet–visible spectrophotometer (Shimadzu) with an experimentally determined standard curve. The absolute flow rate of each input channel is calculated from this quantity, the initial concentration of the dye solutions and the time of collection. Bright-field images and videos of flow were obtained using an inverted microscope (CKX41, Olympus) equipped with a CCD (charge-coupled device) colour camera (KP-D20BU, Hitachi). In this case, red and blue food colouring was used for visualization, as shown in Fig. 4. Image analysis was done using ImageJ software (NIH shareware, http://rsb.info.nih.gov/ij/index.html). The temporal history traces in Fig. 4d were calculated from each frame (such as those in Fig. 4c) of collected video during actuation. The images were split according to RGB colour, optimized for brightness and contrast, and then the red and blue optical intensities were recorded in a rectangular region in the output channel (green intensity discarded) as a function of time.
References
Unger, M. A., Chou, H. P., Thorsen, T., Scherer, A. & Quake, S. R. Monolithic microfabricated valves and pumps by soft lithography. Science 288, 113–116 (2000).
Burns, M. A. et al. An integrated nanoliter DNA analysis device. Science 282, 484–487 (1998).
Maerkl, S. J. & Quake, S. R. A systems approach to measuring the binding energy landscapes of transcription factors. Science 315, 233–237 (2007).
Easley, C. J. et al. A fully integrated microfluidic genetic analysis system with sample-in-answer-out capability. Proc. Natl Acad. Sci. USA 103, 19272–19277 (2006).
Blazej, R. G., Kumaresan, P. & Mathies, R. A. Microfabricated bioprocessor for integrated nanoliter-scale Sanger DNA sequencing. Proc. Natl Acad. Sci. USA 103, 7240–7245 (2006).
Thorsen, T., Maerkl, S. J. & Quake, S. R. Microfluidic large-scale integration. Science 298, 580–584 (2002).
Grover, W. H., Skelley, A. M., Liu, C. N., Lagally, E. T. & Mathies, R. A. Monolithic membrane valves and diaphragm pumps for practical large-scale integration into glass microfluidic devices. Sensors Actuators B 89, 315–323 (2003).
Kim, J. Y. et al. Photopolymerized check valve and its integration into a pneumatic pumping system for biocompatible sample delivery. Lab Chip 6, 1091–1094 (2006).
Grover, W. H., Ivester, R. H. C., Jensen, E. C. & Mathies, R. A. Development and multiplexed control of latching pneumatic valves using microfluidic logic structures. Lab Chip 6, 623–631 (2006).
Chen, G., Svec, F. & Knapp, D. R. Light-actuated high pressure-resisting microvalve for on-chip flow control based on thermo-responsive nanostructured polymer. Lab Chip 8, 1198–1204 (2008).
Loverich, J., Kanno, I. & Kotera, H. Single-step microfluidic check valve for rectifying and sensing low Reynolds number flow. Microfluid. Nanofluid. 3, 427–435 (2007).
Yu, Q., Bauer, J. M., Moore, J. S. & Beebe, D. J. Responsive biomimetic hydrogel valve for microfluidics. Appl. Phys. Lett. 78, 2589–2591 (2001).
Bao, J. B. & Harrison, D. J. Measurements of flow in microfluidic networks with micrometer-sized flow restrictors. AIChE J. 52, 75–85 (2006).
Leslie, D. C., Easley, C. J., Landers, J. P., Utz, M. & Begley, M. R. Proc. μTAS 2007 Vol. 2, 1489–1491 (2007).
Kim, D., Chesler, D. C. & Beebe, D. J. A method for dynamic system characterization using hydraulic series resistance. Lab Chip 6, 639–644 (2006).
Begley, M. R. & Monahan, J. D. in Handbook of Capillary and Microchip Electrophoresis and Associated Microtechniques 3rd edn, (ed. Landers, J. P.) Ch. 39, 1121–1149 (CRC Press, 2008).
Easley, C. J. et al. Extrinsic Fabry–Perot interferometry for non-contact temperature control of nanoliter volume enzymatic reactions in glass microchips. Anal. Chem. 77, 1038–1045 (2003).
Huang, C.-W. & Lee, G.-B. A microfluidic system for automatic cell culture. J. Micromech. Microeng. 17, 1266–1274 (2007).
Begley, M. R. & Utz, M. Proc. μTAS 2008 Vol. 2, 1351–1353 (2008).
Acknowledgements
D.C.L. acknowledges support from the National Institutes of Health Biotechnology Training Grant at the University of Virginia. C.J.E. acknowledges valuable support from Eli Lilly and Company, through the American Chemical Society’s Division of Analytical Chemistry. M.R.B. gratefully acknowledges the support of the National Science Foundation, through awards CMII No. 0529076 and CMII No. 0800790. J.P.L. thankfully acknowledges support from the National Institutes of Health, through award 5R01HG001832-07.
Author information
Authors and Affiliations
Contributions
D.C.L., C.J.E., J.M.K. and E.S. designed and fabricated the devices and instrumentation, devised and carried out experiments and carried out data analysis. M.U. and M.R.B. generated the models that drove the iterative device development, devised experiments and carried out data analysis. J.P.L. devised experiments. M.R.B. and J.P.L. provided overall guidance to the project and contributed materials. All authors were involved in the writing of the manuscript.
Corresponding authors
Supplementary information
Supplementary Information
Supplementary Informations (PDF 388 kb)
Supplementary Information
Supplementary Movies 1 (AVI 4254 kb)
Rights and permissions
About this article
Cite this article
Leslie, D., Easley, C., Seker, E. et al. Frequency-specific flow control in microfluidic circuits with passive elastomeric features. Nature Phys 5, 231–235 (2009). https://doi.org/10.1038/nphys1196
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1196
This article is cited by
-
A compact modularized power-supply system for stable flow generation in microfluidic devices
Microfluidics and Nanofluidics (2023)
-
A passive Stokes flow rectifier for Newtonian fluids
Scientific Reports (2021)
-
Microfluidic channels of adjustable height using deformable elastomer
Microfluidics and Nanofluidics (2021)
-
Generation and application of sub-kilohertz oscillatory flows in microchannels
Microfluidics and Nanofluidics (2020)
-
Braess’s paradox and programmable behaviour in microfluidic networks
Nature (2019)