Abstract
Entanglement—once only a subject of disputes about the foundation of quantum mechanics—has today become an essential issue in the emerging field of quantum information processing, promising a number of applications, including secure communication, teleportation and powerful quantum computation. Therefore, a focus of current experimental work in the field of quantum information is the creation and manipulation of entangled quantum systems. Here, we present our results on entangling two qubits in an ion-trap quantum processor not through a direct interaction of the ion qubits but instead through the action of a protocol known as entanglement swapping1. Our ion-trap system enables us to implement all steps of the entanglement swapping protocol in a fully deterministic way. Thus, two ion qubits can be prepared on demand in a well-defined entangled state. This particular feature may facilitate the implementation of quantum repeaters2 or aid in distributing entangled states in ion-trap quantum computers3.
Similar content being viewed by others
Main
Entanglement among quantum systems usually results from a common origin of the systems or a direct local interaction between the systems. In both cases, the entangling operation requires the systems to be at the same point in space at a certain time. In entanglement swapping, however, the entangling operation is achieved as follows: starting from two entangled pairs, A1A2 and B1B2, a joint measurement of A2 and B2 in the Bell basis projects pair A1B1 in an entangled state even though A1 and B1 might be far apart. This can be used for applications such as quantum communication or teleportation, which require that quantum systems at distant locations are entangled. Entanglement swapping facilitates the provision of such separated pairs of entangled systems, as two quantum systems in two distinct locations can be entangled through a chain of intermediary entangled pairs. Furthermore, if entanglement swapping is combined with entanglement purification, as proposed in quantum repeater schemes2, the final entangled state can have a higher fidelity than is achievable with a direct transfer of an entangled system. Up to now, entanglement swapping has been implemented with photon pairs4,5 and with ion–photon entangled states6. These implementations are appealing as the photons can be easily used to transfer quantum information over large distances. However, in these experiments, successful entanglement swapping events could only be established probabilistically for a small subset of all states. In contrast, quantum information processing with a system of trapped ions has the advantage that all basic operations for handling quantum information are implemented with high fidelities and, in particular, in a completely deterministic fashion. This capability has been demonstrated in various experiments, for example by implementing a completely deterministic quantum teleportation protocol between trapped-ion qubits7,8. Here, we apply the techniques of these experiments to implement an entanglement swapping protocol for four trapped-ion qubits. In contrast to a previous realization with trapped ions that generated an entangled state at a distance of approximately one metre6, this realization is fully deterministic. Entanglement purification, a protocol equally important for the generation of distant entanglement, has been demonstrated in ref. 9. This experiments shows a similar level of control of four ions as our experiment, but does not feature a deterministic control of the final state.
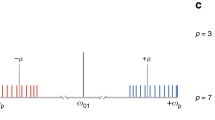
In the experiments described here, deterministic entanglement swapping is implemented with strings of 40Ca+ ions confined in a linear Paul trap. Each ion represents a qubit, where quantum information is stored in a superposition of the |S〉≡S1/2(m=−1/2) ground state and the metastable |D〉≡D5/2(m=−1/2) state. In addition, the ion string undergoes a harmonic motion in the trap potential. For our purpose, we only consider the centre-of-mass vibrational mode along the trap axis at a frequency of ωz=2π1.2 MHz. Laser cooling and optical pumping enable us to prepare the centre-of-mass mode in its ground state |n=0〉 and to initialize all qubits in the state |S〉 (ref. 10). After initialization to  , the quantum state of the ion string is manipulated by applying laser pulses resonant with the
, the quantum state of the ion string is manipulated by applying laser pulses resonant with the  transition to individual ions. This interaction is precisely controlled by setting the frequency, length, phase and intensity of the pulses. Two kinds of operation are used: (1) laser pulses at the resonance frequency, ω0, of the
transition to individual ions. This interaction is precisely controlled by setting the frequency, length, phase and intensity of the pulses. Two kinds of operation are used: (1) laser pulses at the resonance frequency, ω0, of the  transition, which implement single-qubit rotations and (2) laser pulses at the blue-sideband frequency, ω0+ωz, which change the electronic state of the addressed ion as well as the vibrational state of the ion string. The latter kind of operation enables us to implement quantum gates between arbitrary ions in the ion string mediated by the vibrational mode. The quantum state of the qubits is measured by scattering light on the
transition, which implement single-qubit rotations and (2) laser pulses at the blue-sideband frequency, ω0+ωz, which change the electronic state of the addressed ion as well as the vibrational state of the ion string. The latter kind of operation enables us to implement quantum gates between arbitrary ions in the ion string mediated by the vibrational mode. The quantum state of the qubits is measured by scattering light on the  transition at 397 nm and observing the resulting resonance fluorescence with a CCD (charge-coupled device) camera. This corresponds to a projective measurement of the qubits in the {|S〉,|D〉} basis, where the observation of resonance fluorescence at 397 nm indicates a projection to the |S〉 state, whereas the absence of fluorescence indicates a projection to the |D〉 state. Further details of the experimental set-up and methods are given in ref. 10.
transition at 397 nm and observing the resulting resonance fluorescence with a CCD (charge-coupled device) camera. This corresponds to a projective measurement of the qubits in the {|S〉,|D〉} basis, where the observation of resonance fluorescence at 397 nm indicates a projection to the |S〉 state, whereas the absence of fluorescence indicates a projection to the |D〉 state. Further details of the experimental set-up and methods are given in ref. 10.
Entanglement swapping is realized in our experimental set-up as shown in Fig. 1. Initially a string of four 40Ca+ ions is prepared in the state |S S S S,0〉 (the order of the ions is |ion 4…ion 2 ion 1,0〉). First, two pairs of entangled states are prepared. This is achieved by a sequence of three laser pulses that is first applied to ions 1 and 2, and later to ions 3 and 4, and that prepares each pair in the state  with i,j∈{1,…,4}. The total state of the ion string
with i,j∈{1,…,4}. The total state of the ion string  is rewritten by grouping the unentangled ions 2,3 and 1,4 into pairs and expressing their state in terms of the Bell states
is rewritten by grouping the unentangled ions 2,3 and 1,4 into pairs and expressing their state in terms of the Bell states  and
and  as:
as:

Ions 2 and 3 are mapped to the state Ψ− by a Bell measurement on ions 1,4 and subsequent conditional rotations. During the sequence, the quantum information of some qubits is protected from 397 nm light by shifting their S-state population to the D manifold (see the Methods section), denoted in the scheme as ‘Hide’ and the inverse operation as ‘Hide−1’. The time during which the information is hidden is indicated by a grey line.
Writing the state in this way, the procedure for entanglement swapping can be directly inferred: after a projective measurement of either pair (1,4 or 2,3) in the Bell basis, the other pair will be in an entangled state; thus, two ions become entangled that have not previously interacted. The required Bell measurement is achieved in our experiment by mapping the Bell state basis, {|Φ±〉,|Ψ±〉}, onto the product state basis, {|D D〉,|D S〉,|S D〉,|S S〉}, in which a projective measurement is easily possible in our experimental set-up. Consider for example that the Bell measurement is applied to ions 1,4 to entangle ions 2,3 (see the Methods section). This map is implemented by a controlled-NOT (CNOT) gate11, with ion 1 as the control and ion 4 as the target qubit, followed by a π/2 rotation on the control qubit. After this step, the total state of the ion string is given by:

The extra phase factors, exp(i φ) with  , are caused by the CNOT gate but are ignored owing to the subsequent projective measurement. The states of ions 1 and 4 are measured by exposing the ion string for 300 μs with light at 397 nm and observing the resonance fluorescence of the ions with a photomultiplier tube. The quantum information stored in the other ions is protected from the 397 nm light during the measurements (see the Methods section). From equation (1) it can be seen that the observed state of ions 1 and 4 exactly correlates with the entangled state of ions 2 and 3 (either Φ+, Φ−, Ψ+, Ψ−). This fact enables us to create a well-defined entangled output state, which is a requirement for further use of this newly entangled state in protocols such as teleportation or purification. The result of this Bell measurement determines which single-qubit rotation is to be applied to ions 2 or 3 to obtain the desired entangled state. We choose |Ψ23−〉 as the desired output state and note that
, are caused by the CNOT gate but are ignored owing to the subsequent projective measurement. The states of ions 1 and 4 are measured by exposing the ion string for 300 μs with light at 397 nm and observing the resonance fluorescence of the ions with a photomultiplier tube. The quantum information stored in the other ions is protected from the 397 nm light during the measurements (see the Methods section). From equation (1) it can be seen that the observed state of ions 1 and 4 exactly correlates with the entangled state of ions 2 and 3 (either Φ+, Φ−, Ψ+, Ψ−). This fact enables us to create a well-defined entangled output state, which is a requirement for further use of this newly entangled state in protocols such as teleportation or purification. The result of this Bell measurement determines which single-qubit rotation is to be applied to ions 2 or 3 to obtain the desired entangled state. We choose |Ψ23−〉 as the desired output state and note that  , where I is the identity operator and X and Z are Pauli operators. To map ions 2,3 deterministically to |Ψ−〉, first the fluorescence counts measured with the photomultiplier tube are evaluated and the states of ions 1 and 4 are determined. Then depending on this result, laser pulses are applied to ion 3, which implement the required X and Z operations.
, where I is the identity operator and X and Z are Pauli operators. To map ions 2,3 deterministically to |Ψ−〉, first the fluorescence counts measured with the photomultiplier tube are evaluated and the states of ions 1 and 4 are determined. Then depending on this result, laser pulses are applied to ion 3, which implement the required X and Z operations.
The protocol described above is experimentally implemented by the sequence of laser pulses given in Table 1. To prove that this sequence properly implements entanglement swapping, we analyse the output state ρ23 of ions 2 and 3 by quantum state tomography. This requires that a complete tomographic data set is recorded, from which ρ23 is reconstructed12. First, to check whether the protocol is working as expected, we omit the conditional rotations and measure the quantum state directly after the rotation of the Bell basis onto the product basis. At this point of the protocol, the ion string is expected to be in the state given in equation (1). Here, the reconstruction of ρ23 would yield only a completely mixed state, if the result of the Bell measurement on ions 1 and 4 is neglected. However, sorting the tomographic data set with respect to the result of the Bell measurement and then reconstructing ρ23 for each data subset yields the result shown in Fig. 2. For each Bell measurement result, we observe ions 2 and 3 to be in the entangled state expected from equation (1) with fidelities ranging between 76% and 91%, and an entanglement of formation between 0.49 and 0.75 (ref. 13). This is sufficient to prove that the entanglement swapping protocol is working, but requires a post-processing procedure as described above. On the other hand, by implementing the complete protocol including the conditional rotations our scheme becomes completely deterministic, and the final state of ions 2 and 3 will always be |Ψ−〉 irrespective of the Bell measurement result. Figure 3 shows the measured density matrix of ions 2 and 3 for this case. For the reconstruction of this density matrix, the state of ions 1 and 4 was neglected and no further post-processing of the data set was applied. Indeed, ions 2 and 3 are deterministically mapped onto state |Ψ−〉 with a fidelity of 〈Ψ−|ρ23|Ψ−〉=79(2)%. In addition, this state violates a Clauser–Horne–Shimony–Holt inequality14 as 〈A〉=2.18(8)>2, where  with σz±x=σz±σx. The achieved fidelity is mainly limited by the imperfect fidelities of the initial Bell states (≈96%) and of the CNOT gate operation (≈93%; ref. 11).
with σz±x=σz±σx. The achieved fidelity is mainly limited by the imperfect fidelities of the initial Bell states (≈96%) and of the CNOT gate operation (≈93%; ref. 11).
The tomographic data set has been sorted with respect to the result of the Bell measurement. For each of the four subsets, the density matrix of ions 2 and 3 was reconstructed. a–d, The real part of the obtained density matrices for the Bell measurement results |D D〉 (a), |D S〉 (b), |S D〉 (c) and |S S〉 (d). The density matrices show ions 2 and 3 to be in the state expected from equation (1), with fidelities of 76(5)% (a), 82(5)% (b), 81(5)% (c) and 91(3)% (d). Here, the error is due to statistical uncertainties in the tomographic measurements12.
In summary, we have demonstrated how ion qubits that never interacted are entangled through the action of entanglement swapping. In particular, we have realized this scheme in a completely deterministic manner. Within the bounds of the measured fidelity, we achieve entanglement swapping in every single experimental run and then prepare the target ions in a well-defined entangled state. This scheme will find various applications in the future, for example in an implementation of quantum repeaters as proposed in ref. 2. For this, the presented entanglement swapping protocol would be combined with entanglement purification9 to generate entangled qubit pairs of high fidelity at distant locations. A practical implementation of this scheme will require an efficient photon–ion qubit interface15,16. Another application of the entanglement swapping protocol will be in large-scale ion-trap quantum computers3, where it can help to prepare entangled pairs of qubits for quantum teleportation, to connect distant regions of the quantum processor, while minimizing the need to transport ions between distinct trap locations.
Methods
To achieve the reported entanglement swapping fidelity, we have to take several measures, to counteract possible error sources in our experimental set-up. A major concern are addressing errors, that is, the fact that every laser pulse not only manipulates the correct ion but also carries out an unwanted operation on the neighbouring ion(s)10. This error source motivates the choice of ions 1 and 4 for the Bell measurement, such that a major part of the pulse sequence is carried out on the outer ions, where addressing errors are smaller as only one neighbouring ion is present.
During the measurement of either ion 1 or 4, the quantum information in all other ions has to be preserved from the destructive influence of the 397 nm light. For this purpose, we shift the S-state population of these ions to the Zeeman level D′=D5/2(m=−5/2), such that the quantum information is completely encoded in the D5/2 state17. Ions 2 and 3 are transferred to this state directly after the initial Bell states are prepared. This transfer also minimizes addressing errors due to laser pulses applied to ions 1 and 4. A problem arises because quantum information encoded in the D state is highly susceptible to phase shifts caused by magnetic field variations. We counter this problem by applying a spin-echo sequence after approximately half of the pulse sequence to cancel out phase shifts due to low-frequency magnetic field changes18.
References
Zukowski, M., Zeilinger, A., Horne, M. A. & Ekert, A. K. ‘Event-ready-detectors’ Bell experiment via entanglement swapping. Phys. Rev. Lett. 71, 4287–4290 (1993).
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: The role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Kielpinski, D., Monroe, C. & Wineland, D. J. Architecture for a large-scale ion-trap quantum computer. Nature 417, 709–711 (2002).
Pan, J.-W., Bouwmeester, D., Weinfurter, H. & Zeilinger, A. Experimental entanglement swapping: Entangling photons that never interacted. Phys. Rev. Lett. 80, 3891–3894 (1998).
Halder, M. et al. Entangling independent photons by time measurement. Nature Phys. 3, 692–695 (2007).
Moehring, D. L. et al. Entanglement of single-atom quantum bits at a distance. Nature 449, 68–71 (2007).
Riebe, M. et al. Deterministic quantum teleportation with atoms. Nature 429, 734–737 (2004).
Barrett, M. D. et al. Deterministic quantum teleportation of atomic qubits. Nature 429, 737–739 (2004).
Reichle, R. et al. Experimental purification of two-atom entanglement. Nature 443, 838–841 (2006).
Schmidt-Kaler, F. et al. How to realize a universal quantum gate with trapped ions. Appl. Phys. B 77, 789–796 (2003).
Riebe, M. et al. Process tomography of ion trap quantum gates. Phys. Rev. Lett. 97, 220407 (2006).
Roos, C. F. et al. Bell states of atoms with ultralong lifetimes and their tomographic state analysis. Phys. Rev. Lett. 92, 220402 (2004).
Wootters, W. K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245–2248 (1998).
Clauser, J. F., Horne, M. A., Shimony, A. & Holt, R. A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880–884 (1969).
Boozer, A. D., Boca, A., Miller, R., Northup, T. E. & Kimble, H. J. Reversible state transfer between light and a single trapped atom. Phys. Rev. Lett. 98, 193601 (2007).
Cirac, J. I., Zoller, P., Kimble, H. J. & Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221–3224 (1997).
Roos, C. F. et al. Control and measurement of three-qubit entangled states. Science 304, 1478–1480 (2004).
Hahn, E. L. Spin echoes. Phys. Rev. 80, 580–594 (1950).
Acknowledgements
We gratefully acknowledge support by the Austrian Science Fund (FWF), the European Commission (SCALA, CONQUEST networks) and the Institut für Quanteninformation GmbH. This material is based on work supported in part by the U.S. Army Research Office.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Riebe, M., Monz, T., Kim, K. et al. Deterministic entanglement swapping with an ion-trap quantum computer. Nature Phys 4, 839–842 (2008). https://doi.org/10.1038/nphys1107
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1107
This article is cited by
-
Progress in quantum teleportation
Nature Reviews Physics (2023)
-
Probing tripartite entanglement and coherence dynamics in pure and mixed independent classical environments
Quantum Information Processing (2021)
-
Conditional teleportation of quantum-dot spin states
Nature Communications (2020)
-
Comparison the performance of five-qubit IBM quantum computers in terms of Bell states preparation
Quantum Information Processing (2020)
-
Demonstration of entanglement purification and swapping protocol to design quantum repeater in IBM quantum computer
Quantum Information Processing (2019)