Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Quantum transport simulations in a programmable nanophotonic processor

Nature Photonics volume 11, pages 447–452 (2017)Cite this article

Subjects

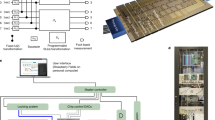
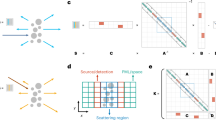
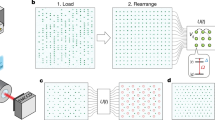
Abstract

Environmental noise and disorder play critical roles in quantum particle and wave transport in complex media, including solid-state and biological systems. While separately both effects are known to reduce transport, recent work predicts that in a limited region of parameter space, noise-induced dephasing can counteract localization effects, leading to enhanced quantum transport. Photonic integrated circuits are promising platforms for studying such effects, with a central goal of developing large systems providing low-loss, high-fidelity control over all parameters of the transport problem. Here, we fully map the role of disorder in quantum transport using a nanophotonic processor: a mesh of 88 generalized beamsplitters programmable on microsecond timescales. Over 64,400 experiments we observe distinct transport regimes, including environment-assisted quantum transport and the ‘quantum Goldilocks’ regime in statically disordered discrete-time systems. Low-loss and high-fidelity programmable transformations make this nanophotonic processor a promising platform for many-boson quantum simulation experiments.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Figure 1: A quantum transport simulator.
Figure 2: Programmable nanophotonic processor.
Figure 3: Convergence and the full noisy transport space.
Figure 4: Environment-assisted quantum transport and the Goldilocks regime.

References

  1. Schmitz, H. et al. Quantum walk of a trapped ion in phase space. Phys. Rev. Lett. 103, 090504 (2009).

    Article  ADS  Google Scholar 

  2. Zahringer, F. et al. Realization of a quantum walk with one and two trapped ions. Phys. Rev. Lett. 104, 100503 (2010).

    Article  ADS  Google Scholar 

  3. Preiss, P. M. et al. Strongly correlated quantum walks in optical lattices. Science 347, 1229–1233 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  4. Broome, M. A. et al. Discrete single-photon quantum walks with tunable decoherence. Phys. Rev. Lett. 104, 153602 (2010).

    Article  ADS  Google Scholar 

  5. Svozilik, J., Leon-Montiel, R. d. J. & Torres, J. P. Implementation of a spatial two-dimensional quantum random walk with tunable decoherence. Phys. Rev. A 86, 052327 (2012).

    Article  ADS  Google Scholar 

  6. Kitagawa, T. et al. Observation of topologically protected bound states in photonic quantum walks. Nat. Commun. 3, 882 (2012).

    Article  ADS  Google Scholar 

  7. Schreiber, A. et al. Photons walking the line: a quantum walk with adjustable coin operations. Phys. Rev. Lett. 104, 050502 (2010).

    Article  ADS  Google Scholar 

  8. Crespi, A. et al. Anderson localization of entangled photons in an integrated quantum walk. Nat. Photon. 7, 322–328 (2013).

    Article  ADS  Google Scholar 

  9. Schwartz, T., Bartal, G., Fishman, S. & Segev, M. Transport and Anderson localization in disordered two-dimensional photonic lattices. Nature 446, 52–55 (2007).

    Article  ADS  Google Scholar 

  10. Lahini, Y. et al. Anderson localization and nonlinearity in one-dimensional disordered photonic lattices. Phys. Rev. Lett. 100, 013906 (2008).

    Article  ADS  Google Scholar 

  11. Schreiber, A. et al. Decoherence and disorder in quantum walks: from ballistic spread to localization. Phys. Rev. Lett. 106, 180403 (2011).

    Article  ADS  Google Scholar 

  12. Bromberg, Y., Lahini, Y., Morandotti, R. & Silberberg, Y. Quantum and classical correlations in waveguide lattices. Phys. Rev. Lett. 102, 253904 (2009).

    Article  ADS  Google Scholar 

  13. Peruzzo, A. et al. Quantum walks of correlated photons. Science 329, 1500–1503 (2010).

    Article  ADS  Google Scholar 

  14. Sansoni, L. et al. Two-particle bosonic–fermionic quantum walk via integrated photonics. Phys. Rev. Lett. 108, 010502 (2012).

    Article  ADS  Google Scholar 

  15. Liu, C. et al. Enhanced energy storage in chaotic optical resonators. Nat. Photon. 7, 473–478 (2013).

    Article  ADS  Google Scholar 

  16. Defienne, H., Barbieri, M., Walmsley, I. A., Smith, B. J. & Gigan, S. Two-photon quantum walk in a multimode fiber. Sci. Adv. 2, e1501054 (2016).

    Article  ADS  Google Scholar 

  17. Wolterink, T. A. et al. Programmable two-photon quantum interference in 103 channels in opaque scattering media. Phys. Rev. A 93, 053817 (2016).

    Article  ADS  Google Scholar 

  18. Harris, N. C. et al. Integrated source of spectrally filtered correlated photons for large-scale quantum photonic systems. Phys. Rev. X 4, 041047 (2014).

    Google Scholar 

  19. Collins, M. et al. Integrated spatial multiplexing of heralded single-photon sources. Nat. Commun. 4, 2582 (2013).

    Article  ADS  Google Scholar 

  20. Silverstone, J. W. et al. On-chip quantum interference between silicon photon-pair sources. Nat. Photon. 8, 104–108 (2014).

    Article  ADS  Google Scholar 

  21. Najafi, F. et al. On-chip detection of non-classical light by scalable integration of single-photon detectors. Nat. Commun. 6, 5873 (2015).

    Article  ADS  Google Scholar 

  22. Aspuru-Guzik, A. & Walther, P. Photonic quantum simulators. Nat. Phys. 8, 285–291 (2012).

    Article  Google Scholar 

  23. Huh, J., Guerreschi, G. G., Peropadre, B., McClean, J. R. & Aspuru-Guzik, A. Boson sampling for molecular vibronic spectra. Nat. Photon. 9, 615–620 (2015).

    Article  ADS  Google Scholar 

  24. Levi, L., Krivolapov, Y., Fishman, S. & Segev, M. Hyper-transport of light and stochastic acceleration by evolving disorder. Nat. Phys. 8, 912–917 (2012).

    Article  Google Scholar 

  25. Amir, A., Lahini, Y. & Perets, H. B. Classical diffusion of a quantum particle in a noisy environment. Phys. Rev. E 79, 050105 (2009).

    Article  ADS  Google Scholar 

  26. Anderson, P. W. Absence of diffusion in certain random lattices. Phys. Rev. 109, 1492–1505 (1958).

    Article  ADS  Google Scholar 

  27. Lahini, Y., Bromberg, Y., Christodoulides, D. N. & Silberberg, Y. Quantum correlations in two-particle Anderson localization. Phys. Rev. Lett. 105, 163905 (2010).

    Article  ADS  Google Scholar 

  28. Segev, M., Silberberg, Y. & Christodoulides, D. N. Anderson localization of light. Nat. Photon. 7, 197–204 (2013).

    Article  ADS  Google Scholar 

  29. Rebentrost, P., Mohseni, M., Kassal, I., Lloyd, S. & Aspuru-Guzik, A. Environment-assisted quantum transport. New J. Phys. 11, 033003 (2009).

    Article  ADS  Google Scholar 

  30. Mohseni, M., Rebentrost, P., Lloyd, S. & Aspuru-Guzik, A. Environment-assisted quantum walks in photosynthetic energy transfer. J. Chem. Phys. 129, 174106 (2008).

    Article  ADS  Google Scholar 

  31. Reck, M. & Zeilinger, A. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 73, 58–61 (1994).

    Article  ADS  Google Scholar 

  32. Miller, D. A. B. Self-configuring universal linear optical component. Photon. Res. 1, 1–15 (2013).

    Article  ADS  Google Scholar 

  33. Mower, J., Harris, N. C., Steinbrecher, G. R., Lahini, Y. & Englund, D. High-fidelity quantum state evolution in imperfect photonic integrated circuits. Phys. Rev. A 92, 032322 (2015).

    Article  ADS  Google Scholar 

  34. Lloyd, S., Mohseni, M., Shabani, A. & Rabitz, H. The quantum Goldilocks effect: on the convergence of timescales in quantum transport. Preprint at http://arxiv.org/abs/1111.4982 (2011).

  35. Carolan, J. et al. Universal linear optics. Science 349, 711–716 (2015).

    Article  MathSciNet  Google Scholar 

  36. Harris, N. C. et al. Efficient, compact and low loss thermo-optic phase shifter in silicon. Opt. Express 22, 10487–10493 (2014).

    Article  ADS  Google Scholar 

  37. Aaronson, S. & Arkhipov, A. in Proc. 43rd Annual ACM Symposium on Theory of Computing (eds Fortnow, L. & Vadhan, S.) 333–342 (ACM, 2011).

    MATH  Google Scholar 

  38. Spring, J. B. et al. Boson sampling on a photonic chip. Science 339, 798–801 (2012).

    Article  ADS  Google Scholar 

  39. Broome, M. A. et al. Photonic boson sampling in a tunable circuit. Science 339, 794–798 (2012).

    Article  ADS  Google Scholar 

  40. Prevedel, R. et al. High-speed linear optics quantum computing using active feed-forward. Nature 445, 65–69 (2007).

    Article  ADS  Google Scholar 

  41. Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).

    Article  ADS  Google Scholar 

  42. Kok, P. et al. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 79, 135–174 (2007).

    Article  ADS  Google Scholar 

  43. Childs, A. M. Universal computation by quantum walk. Phys. Rev. Lett. 102, 180501 (2009).

    Article  ADS  MathSciNet  Google Scholar 

  44. Baehr-Jones, T. et al. A 25 Gb/s silicon photonics platform. Preprint at http://arxiv.org/abs/1203.0767 (2012).

  45. Kempe, J. Quantum random walks: an introductory overview. Contemp. Phys. 44, 307–327 (2003).

    Article  ADS  Google Scholar 

  46. Notaros, J. et al. in Optical Fiber Communications Conference and Exhibition (OFC), 1–3 (IEEE, 2016).

  47. Cardenas, J. et al. Low loss etchless silicon photonic waveguides. Opt. Express 17, 4752–4757 (2009).

    Article  ADS  Google Scholar 

  48. Wilkes, C. M. et al. 60 dB high-extinction auto-configured Mach–Zehnder interferometer. Opt. Lett. 41, 5318–5321 (2016).

    Article  ADS  Google Scholar 

  49. Yao, X.-C. et al. Observation of eight-photon entanglement. Nat. Photon. 6, 225–228 (2012).

    Article  ADS  Google Scholar 

  50. Silverstone, J. W. et al. Qubit entanglement between ring-resonator photon-pair sources on a silicon chip. Nat. Commun. 6, 7948 (2015).

    Article  ADS  Google Scholar 

  51. Gerrits, T. et al. On-chip, photon-number-resolving, telecommunication-band detectors for scalable photonic information processing. Phys. Rev. A 84, 060301 (2011).

    Article  ADS  Google Scholar 

  52. McCaughan, A. N. & Berggren, K. K. A superconducting-nanowire three-terminal electrothermal device. Nano Lett. 14, 5748–5753 (2014).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

N.C.H. and M.P. acknowledge support from the National Science Foundation Graduate Research Fellowship Program grants 1122374 and 1122374, respectively. G.S. acknowledges support from the Department of Defense National Science and Engineering Graduate Fellowship. Y.L. acknowledges support from the Pappalardo Fellowship in Physics. This work was supported in part by the Air Force Office of Scientific Research (AFOSR) Multidisciplinary University Research Initiative (FA9550-14-1-0052) and the Air Force Research Laboratory programme (FA8750-14-2-0120). M.H. acknowledges support from the AFOSR Small Business Technology Transfer programme (FA9550-12-C-0079 and FA9550-12-C-0038) and G. Pomrenke, of AFOSR, for his support of the optoelectronic systems integration in silicon (OpSIS) effort, through a Presidential Early Career Award in Science and Engineering award (FA9550-13-1-0027) and funding for OpSIS (FA9550-10-1-0439). D.E. acknowledges support by Excitonics, an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under award no. desc0001088. The authors thank C. Galland for his discussions about the result.

Author information

Authors and Affiliations

  1. Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, 02139, Massachusetts, USA

    Nicholas C. Harris, Gregory R. Steinbrecher, Mihika Prabhu, Jacob Mower & Dirk Englund

  2. Harvard John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, 02138, Massachusetts, USA

    Yoav Lahini

  3. Department of Physics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, 02139, Massachusetts, USA

    Darius Bunandar

  4. Research Laboratory of Electronics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, 02139, Massachusetts, USA

    Changchen Chen & Franco N. C. Wong

  5. Elenion Technologies, 171 Madison Avenue, Suite 1100, New York, 10016, New York, USA

    Tom Baehr-Jones & Michael Hochberg

  6. Department of Mechanical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, 02139, Massachusetts, USA

    Seth Lloyd

Authors
  1. Nicholas C. Harris
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gregory R. Steinbrecher
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mihika Prabhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yoav Lahini
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jacob Mower
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Darius Bunandar
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Changchen Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Franco N. C. Wong
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Tom Baehr-Jones
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Michael Hochberg
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Seth Lloyd
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Dirk Englund
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

N.C.H. designed the photonic integrated circuit and experimental set-up and performed the experiments. N.C.H. laid out the design mask, with assistance from G.S. on metal routing. N.C.H. and M.P. calibrated the system. N.C.H., Y.L., G.S., S.L. and D.E. conceived the experiment. D.B. assisted with the theory. C.C. and F.N.C.W. assisted with multiphoton experiments. T.B.-J. and M.H. fabricated the system. All authors contributed to writing the paper.

Corresponding author

Correspondence to Nicholas C. Harris.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 3371 kb)

Rights and permissions

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Harris, N., Steinbrecher, G., Prabhu, M. et al. Quantum transport simulations in a programmable nanophotonic processor. Nature Photon 11, 447–452 (2017). https://doi.org/10.1038/nphoton.2017.95

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphoton.2017.95

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing